ব্রাকিস্টোক্রোন সমস্যা: গোড়ার কথা

27 Mar 2024 print mode

অঙ্ক নিয়ে ভাবনা কিছু ইতিহাস … পদার্থবিদ্যার কিছু বিস্ময়

%e0%a6%ac%e0%a7%8d%e0%a6%b0%e0%a6%be%e0%a6%95%e0%a6%bf%e0%a6%b8%e0%a7%8d%e0%a6%9f%e0%a7%8b%e0%a6%95%e0%a7%8d%e0%a6%b0%e0%a7%8b%e0%a6%a8-%e0%a6%b8%e0%a6%ae%e0%a6%b8%e0%a7%8d%e0%a6%af%e0%a6%be

অনির্বাণ ঘোষ

"বিজ্ঞান" সম্পাদক

প্রদীপ্ত পঞ্চাধ্যায়ী

কাঁথি প্রভাত কুমার কলেজ

অভিজিৎ কর গুপ্ত

পাঁশকুড়া বনমালী কলেজ

শেষ জীবনে গ্যালিলিও ছিলেন গৃহবন্দী, অসুস্থ, এবং প্রায় অন্ধ। কিন্তু ওঁর চিন্তাভাবনাকে আটকানো যায়নি। তাঁর মাথায় ঘুরতে থাকে মহাকর্ষের প্রভাবে বস্তুর গতিপ্রকৃতির নানান ব্যাপার স্যাপার। যেমন, ধরো কোনো বস্তু মহাকর্ষ বলের প্রভাবে একটা বিন্দু B থেকে আরেকটা বিন্দু A অব্দি নেমে আসছে একটা সরল বা বক্র পথ ধরে। এখানে A সরাসরি B-এর নিচে অবস্থিত নয়। তাহলে পথটার আকৃতি কী হলে বস্তুটার নামতে সবথেকে কম সময় লাগবে? তা কি বৃত্তাকার (circular)? তিনি হয়তো অনুমান করেননি, এই সমস্যা অঙ্ক ও পদার্থবিদ্যার ইতিহাসে এক নতুন পর্যায়ের সূচনা করবে।

গ্যালিলিওর শেষ জীবন: সমস্যার সূত্রপাত

ফ্লোরেন্স শহরের বাইরে ছোট্ট একটা জায়গা আর্সেট্রি। গ্যালিলিও (1564 – 1642) তাঁর জীবনের শেষ দিনগুলো কাটাচ্ছেন এখানে। তাঁরই দীর্ঘদিনের বন্ধু স্বয়ং পোপ-এর কড়া নির্দেশে এখানে গৃহবন্দী তিনি।

এই বন্দিদশার কারণ কী? 1632 সালে প্রকাশিত হয়েছিল তাঁর একটা বই, ‘Dialogue Concerning the Two Chief World Systems’! এখানে তিনি কোপার্নিকাসের তত্ত্বকে তুলে ধরেছিলেন কথোপকথনের মাধ্যমে। পৃথিবী সহ সব গ্রহই যে সূর্যের চারদিকে আবর্তন করে, কোপার্নিকাসের তত্ত্ব তাই বলছিল। অথচ এই ধারণা বাইবেলের তত্ত্বের একেবারে বিপরীত! আর, এখান থেকেই যত বিপত্তি। বিচারের জন্য বৃদ্ধ ও অসুস্থ গ্যালিলিওকে ডেকে পাঠানো হয়েছিল রোমে। বিচার নামক প্রহসনের পর ঠিক হয়েছিল, কড়া নজরে গৃহবন্দী থাকবেন গ্যালিলিও। আর কিছু লেখালেখি করতে পারবেন না।

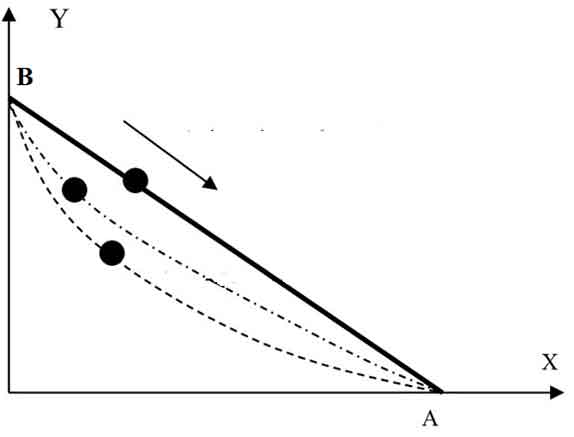
গৃহবন্দী, অসুস্থ, এবং প্রায় অন্ধ গ্যালিলিও বসে বসে ভাবতে থাকেন নানা সমস্যা নিয়ে। কোনো বস্তু মহাকর্ষ বলের প্রভাবে একটা বিন্দু থেকে আরেকটা বিন্দু অব্দি নেমে আসছে একটা সরল বা বক্র পথ ধরে। তাহলে পথটার আকৃতি কী হলে বস্তুটার নামতে সবথেকে কম সময় লাগবে?

গৃহবন্দী, অসুস্থ, এবং প্রায় অন্ধ গ্যালিলিও বসে বসে ভাবতে থাকেন নানা সমস্যা নিয়ে। তার মধ্যে একটা হলো এইটি: ধরো কোনো বস্তু মহাকর্ষ বলের প্রভাবে একটা বিন্দু $B$ থেকে আরেকটা বিন্দু $A$ অব্দি নেমে আসছে একটা সরল বা বক্র পথ ধরে। এখানে $A$ সরাসরি $B$ -এর নিচে অবস্থিত নয়। তাহলে পথটার আকৃতি কী হলে বস্তুটার নামতে সবথেকে কম সময় লাগবে? তা কি বৃত্তাকার (circular)? তার মানে, একটা বৃত্তাংশ (circular arc) বরাবর নেমে এলে কি সবচেয়ে কম সময় লাগবে? ভূমিকম্পের সময় চার্চের সিলিং থেকে ঝোলানো লম্বা কোনো আলোর ঝালরকে হয়তো পেন্ডুলামের মতো বৃত্তাকার পথে দুলতে দেখেছিলেন তিনি। সেখান থেকেই বোধহয় তাঁর মাথায় এসেছিল এইরকম একটা ভাবনা!

অভিকর্ষের অধীনে কালো বল সবচেয়ে কম সময়ে কোন পথ বরাবর যাবে?

মনে রাখতে হবে, তখনও ক্যালকুলাস আবিষ্কার হয়নি। কাজেই গতিবিদ্যার সাধারণ সমস্যার সমাধান করাও বেশ জটিল ব্যাপার ছিল তখন। কিন্তু ছবি এঁকে, অভিনব জ্যামিতিক নির্মাণ করে গ্যালিলিও গতিবিদ্যার অনেক প্রাথমিক সমস্যার সমাধান এর আগেই করে ফেলেছিলেন। তাঁর জ্যামিতিক যুক্তিপ্রয়োগ থেকে ক্যালকুলাসের স্পষ্ট পূর্বাভাস পাওয়া যায়! [1]

অভিকর্ষের অধীনে পতনশীল বস্তুর গতি বিবেচনা করে গ্যালিলিও-র জ্যামিতিক নির্মাণ। https://scielo.isciii.es/scielo.php?script=sci_arttext&pid=S0211-95362008000100011

এইরকম ভাবে বহু সমস্যার সমাধান সহ তিনি লিখে ফেললেন আরেকটা বই, তাঁর জীবনের শেষ বই — ‘Discourses and Mathematical Demonstrations Concerning Two New Sciences’! চোরাপথে, চার্চের নজর এড়িয়ে তা ইটালি থেকে চলে গেলো হল্যান্ডে, 1638 সালে। শোনা যায়, বইটা প্রকাশ পাওয়ার পর তার পঞ্চাশটা কপি 1639 সালে রোমের বইয়ের দোকানে আসার সাথে সাথে সব কপি বিক্রি হয়ে যায়, চার্চের লোকেদের নজরে আসার আগেই।

পরবর্তীকালে গণিতজ্ঞ ও পদার্থবিদরা জানতে পারেন গ্যালিলিও বর্ণিত এই সমস্যার কথা। অভিকর্ষের প্রভাবে ন্যূনতম সময়ে কোনো বস্তুর নেমে আসা নিয়ে গ্যালিলিও যে অভিনব জ্যামিতিক প্রমাণ দিয়েছিলেন, সে বিষয়েও তারা জানতে পারেন। সবচেয়ে কম সময়ে নেমে আসার পথ যে কোনো বৃত্তাংশ বরাবর হবে এর নিশ্চিত প্রমাণ না দিলেও গ্যালিলিওর হিসাব যেন সেরকমই কিছু ইঙ্গিত করে।

সবচেয়ে কম সময়ে নেমে আসার পথ যে কোনো বৃত্তাংশ বরাবর হবে এর নিশ্চিত প্রমাণ না দিলেও গ্যালিলিওর হিসাব যেন সেরকমই কিছু ইঙ্গিত করে।

ক্যালকুলাস আবিষ্কার: নিউটন ও লাইবনিজ

তখন সতেরো শতকের শেষের দিক। আইজ্যাক নিউটন (Isaac Newton) এবং গডফ্রায়েড লাইবনিজ (Gottfried Wilhelm Leibniz)-এর কলনবিদ্যা (Calculus) আবিষ্কার হয়ে গেছে। ক্যালকুলাসের সাহায্যে অনেক প্রবলেমের সমাধান করা যাচ্ছে অনায়াসে।

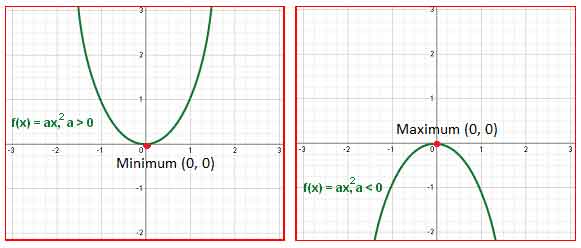
অঙ্ক পড়তে গিয়ে তোমরা গাণিতিক function (অপেক্ষক)-এর সাথে পরিচিত হয়েছো। একটি রাশি (variable) $x$ পরিবর্তনের সাথে সাথে অন্য একটি রাশি $y$ পরিবর্তন হলে আমরা বলি $y$ হল $x$ -এর একটি অপেক্ষক (function)। দুই রাশির মধ্যে এই যোগাযোগকে লেখা হয় $y = f(x)$ এইভাবে। $x$ বাড়ার সাথে সাথে $y$ যেভাবে পরিবর্তিত হয়, তাতে অনেক ক্ষেত্রে দেখা যায় $y$ তার মানের একবার চূড়ায় (maximum) যায় কিংবা তলানিতে (minimum) নামে (নিচের চিত্র)।

তোমরা যারা অন্তরকলন (differential calculus) পড়েছো তারা দেখেছো কীভাবে একটা অপেক্ষক $f(x)$ -এর মিনিমাম কিংবা ম্যাক্সিমাম ( $x_{min}$ বা $x_{max}$ ) বার করা যায় কোথায় তার অবকল সহগের (derivative) মান শূন্য সেটা বের করে:

$\frac{df}{dx}|_{x_{min}, x_{max}} = 0$

সহজ ভাষায় বললে, যে বিন্দুতে $f$ মিনিমাম বা ম্যাক্সিমাম হবে সেইখানে $x$ -এর অতি সামান্য পরিবর্তন ( $dx$ ) করলে $f$ -এর কিন্তু কোনো পরিবর্তন হবে না ( $df = 0$ )।

একটা গাণিতিক অপেক্ষকের মিনিমাম ও ম্যাক্সিমাম (Credit: MyMathEducator.com)।

প্রাথমিক ক্যালকুলাসে যেসব অপেক্ষক নিয়ে কাজ করা হয় সেগুলো একটা সংখ্যা গ্রহণ করে আরেকটা সংখ্যা ফিরিয়ে দেয়, যেমন $f(x) = x^2$ । অনেক সময় তারা একাধিক সংখ্যাও গ্রহণ করতে পারে, যেমন $g(u,v) = u^2 + v^2$ । এদের আমরা বলতে পারি সংখ্যার অপেক্ষক। এই $x$ বা $(u,v)$ -এর যেসব মানের জন্যে অপেক্ষকটা চূড়ায় ওঠে বা তলানিতে নামে তাদের নির্ণয় করাই প্রাথমিক ডিফারেনশিয়াল ক্যালকুলাসের একটা প্রধান কাজ।

কিন্তু নিউটন ও লাইবনিজের সময়েই এইরকম চর্চা থেকে আরো এক ধাপ এগিয়ে ভাবা হয়েছিল আরেকটু জটিল রকম প্রবলেমের কথা। তার একটা উদাহরণ দেওয়া যাক।

গ্যালিলিওর সমস্যা ক্যালকুলাসের ভাষায় কীভাবে বলবো?

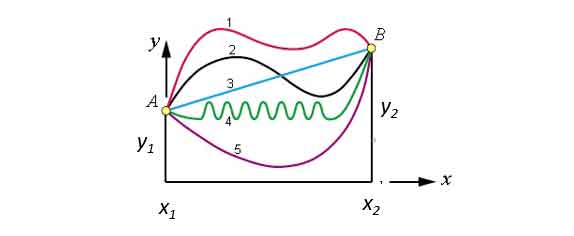
ধরি একটা সমতলে $A (x_1, y_1)$ বিন্দু থেকে $B (x_2, y_2)$ বিন্দুতে একটা বস্তু যাচ্ছে হয় সোজাসুজি কিংবা এঁকেবেঁকে (নিচের চিত্র)। অর্থাৎ বস্তুটার পথকে একটা অপেক্ষক $y = f(x)$ দিয়ে নির্দেশ করা যায়। এই অপেক্ষক $f$ -এর ওপর একমাত্র শর্ত হলো $y_1 = f(x_1)$ এবং $y_2 = f(x_2)$ হতে হবে। কিন্তু $x_1$ এবং $x_2$ -র মাঝে $f$ -এর আকৃতি যা খুশি হতে পারে।

কোন পথ ধরলে AB দূরত্ব সবচেয়ে কম হবে — ক্যালকুলাস দিয়ে খোঁজার চেষ্টা (Credit — MH Mudde)।

বস্তুটা $A (x_1, y_1)$ থেকে $B (x_2, y_2)$ যেতে যতটা পথ অতিক্রম করবে তাকে $F$ দিয়ে নির্দেশ করা যাক। ভেবে দেখো, $F$ -এর মান কিন্তু শুধুমাত্র শুরুর এবং শেষের বিন্দুর স্থানাঙ্কসমূহ, অর্থাৎ $(x_1, y_1, x_2, y_2)$ -এর ওপরেই নির্ভর করে না। সেটা এই দুই বিন্দুর মাঝের সমস্ত বিন্দুতে $f$ অপেক্ষকের মানের ওপরেও নির্ভর করে। $f$ -এর আকৃতি যেই বদলে দেবে, $F$ -এর মানও বদলে যাবে। অর্থাৎ $F$ এমন একটা অদ্ভুত অপেক্ষক যে একটা ‘সংখ্যার অপেক্ষক’-কে গ্রহণ করে একটা সংখ্যাকে ফিরিয়ে দেয়। একে আমরা লিখি $F[f]$ এইভাবে। ‘সংখ্যার অপেক্ষক’-এর অনুকরণে আমরা এর নাম দিতে পারি অপেক্ষকের অপেক্ষক।

তোমরা যারা একটু ইন্টিগ্রাল ক্যালকুলাস পড়েছো তারা ছবি দেখলে বুঝতে পারবে এই $F[f]$ এর গাণিতিক রূপ হচ্ছে

$F[f] = \int_{x_1}^{x_2} \sqrt{(dx)^2 + (dy)^2}$

$= \int_{x_1}^{x_2} dx\sqrt{1 + (\frac{dy}{dx})^2}$

$= \int_{x_1}^{x_2} dx\sqrt{1 + (\frac{df}{dx})^2}$

সুতরাং আমাদের প্রবলেমটাকে এখন লেখা যায় এইভাবে: কোন $f(x)$ -এর জন্যে $F[f]$ -এর মান সর্বনিম্ন হবে। এইটা ঠিক একটা ডিফারেনশিয়াল ক্যালকুলাসের সমস্যার মতোই এখন লাগছে, তাই না? কিন্তু বুঝতেই পারছো স্কুলে পড়া ক্যালকুলাস দিয়ে ঠিক এটার সমাধান করা যাবে না। তার জন্যে লাগবে কিছু নতুন গাণিতিক ধারণা।

সবসময় যে এই ধরনের অঙ্ক কষতে এই নতুন গাণিতিক তত্ত্বের প্রয়োজন আছে, এরকম নয়। যেমন আমাদের অঙ্কটার ক্ষেত্রে, এমনিতেই বলে দেওয়া যায় যে, দুটো বিন্দুর মধ্যে সরলরেখা বরাবর দূরত্ব সবথেকে কম হবে। সুতরাং, স্থানাঙ্ক জ্যামিতি বলে যে আমাদের সমাধান হলো:

$f_{min}(x) = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) + y_1$

এখন ভেবে দেখো, গ্যালিলিওর “দ্রুততম অবতরণের পথ”-এর সমস্যাও কিন্তু ঠিক এইরকম একটা অপেক্ষকের অপেক্ষকের সর্বনিম্ন মান বের করারই সমস্যা।

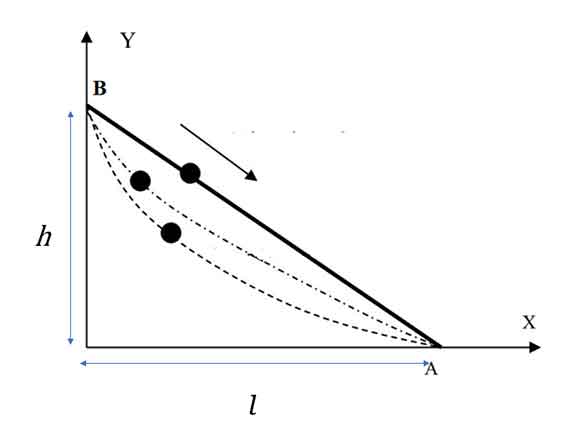
ধরি, একটা বস্তু যাচ্ছে ভূমি থেকে $h$ উচ্চতায় অবস্থিত $B$ বিন্দু থেকে ভূমির ওপর l দূরত্বে অবস্থিত $A$ বিন্দুতে।
তার অবতরণের পথ হলো একটি অপেক্ষক $f(x)$ , যেখানে $f(0) = h$ এবং $f(l) = 0$ ।
সুতরাং, বস্তুটির অবতরণের সময় একটি অপেক্ষকের অপেক্ষক $T[f]$ ।
তাহলে, গ্যালিলিওর প্রশ্ন হলো: কোন $f_{min}(x)$ -এর জন্যে $T[f]$ সর্বনিম্ন?

গ্যালিলিওর অনুমান অনুযায়ী $f_{min}(x)$ একটা বৃত্তাংশ। কিন্তু, নতুন কোনো ক্যালকুলাস দিয়ে কি তার নিশ্চিত উত্তর পাওয়া যেতে পারে?

এই নতুন ক্যালকুলাস কী ধাঁচের হবে তার একটা আন্দাজ কিন্তু এখনি করা যায়। সাধারণ ডিফারেনশিয়াল ক্যালকুলাসের সাথে উপমা টেনে বলতে পারি যে $f_{min}(x)$ বের করতে হলে আমাকে এই ধরনের একটা সমীকরণ সমাধান করতে হবে:

$\frac{\delta T}{\delta f}|_{f_{min}(x)} = 0$

$T[f]$ -এর মতো অপেক্ষকের অপেক্ষকের অবকল সহগ (functional derivative) বার করার উপায় নিউটন বা লাইবনিজ কারোরই জানা ছিল না। তার জন্যে অঙ্কশাস্ত্রের আরও কিছুটা অগ্রসর হওয়ার প্রয়োজন ছিল। সেই উপায় আবিষ্কার করলেন তাঁদের পরের প্রজন্মের গণিতজ্ঞরা — জোহান বার্নোলির ছাত্র লিওনার্ড অয়লার এবং প্রতিভাবান ফরাসী গণিতজ্ঞ জোশেফ ল্যুই লাগ্রাঞ্জ।

তাঁরা এই সমীকরণকে যেভাবে লিখলেন আমাদের কাছে এখন তা অয়লার-লাগ্রাঞ্জ সমীকরণ নামে পরিচিত। তাঁদের গবেষণার ফলে ব্রাকিস্টোক্রোন প্রবলেমের মতো সমস্যার, যাতে একটা ফাংশানালের মিনিমাম (বা ম্যাক্সিমাম) বের করতে হয়, সমাধানের একটা সাধারণ পদ্ধতি বেরোলো। শুধু প্রশ্নের ফাংশানালটা বুঝে তার থেকে সঠিক অয়লার-লাগ্রাঞ্জ সমীকরণটা লিখে তার সমাধান করতে হবে। এই সমাধানের সাধারণ তত্ত্বের নাম দেওয়া হলো ভ্যারিয়েশনাল ক্যালকুলাস (variational calculus)। গণিত ও পদার্থবিদ্যার একটা নতুন দিগন্ত খুলে গেলো।

আমরা এই লেখায় অয়লার-লাগ্রাঞ্জ সমীকরণের তত্ত্বে যাবো না। তার একটা কারণ হলো এই যে ব্রাকিস্টোক্রোন প্রবলেমের গল্প কিন্তু মোটেই ততদিন থেমে থাকেনি। নিউটন, লাইবনিজ, বা বার্নোলির কাছে সমাধানের সাধারণ পদ্ধতি না থাকলে কী হবে, তাঁদের কল্পনাশক্তির অভাব তো ছিল না। নিজেদের জমানার অঙ্কশাস্ত্র কাজে লাগিয়েই তাঁরা নানারকম অভিনব উপায়ে ব্রাকিস্টোক্রোন প্রবলেমের সমাধান করার চেষ্টা করেছিলেন। তাঁদের মধ্যে রেষারেষি এবং তাঁদের এক অভিনব সমাধানের গল্পই আমরা এই লেখায় বলবো।

বার্নোলির চ্যালেঞ্জ: নিউটন কি পারবেন ?

1696 সালের জুন মাসে Acta Eruditorum নামে একটি জার্মান গবেষণা পত্রিকায় গ্যালিলিওর এই প্রশ্নটাই আবার রাখলেন বিখ্যাত গণিতজ্ঞ জোহান বার্নোলি [2]। গ্যালিলিওর “দ্রুততম অবতরণের পথ”-এর সমস্যাটিকে তিনি পৃথিবীর শ্রেষ্ঠ গণিতজ্ঞদের সামনে এক চ্যালেঞ্জ হিসেবে ছুঁড়ে দিলেন (বার্নোলির নিজের ভাষায়: ‘to the most acute mathematicians of the entire world’)! সমস্যাটার নাম দেওয়া হলো — The Brachistochrone problem। গ্রীক শব্দ brachistos (shortest) এবং chronos (time) যোগ করে তৈরি হলো এই নাম।

সেই সময়ে নিউটন, লাইবনিজ, বার্নোলি ভাইদের মতো স্বনামধন্য গণিতজ্ঞরা জানতেন যে গ্যালিলিওর সেই জ্যামিতিক প্রমাণ থেকে সুনির্দিষ্টভাবে কিছু বলা যাবে না। অর্থাৎ, অভিকর্ষের প্রভাবে কোনো বস্তুর নেমে আসার দ্রুততম পথটা একটা বৃত্তাংশ হবেই তার কোনো নিশ্চয়তা নেই। অথচ সাধারণ ক্যালকুলাসের মিনিমাম ও ম্যাক্সিমাম বার করার প্রচলিত পদ্ধতিতেও কিছু করা সম্ভব হচ্ছিল না। কাজেই, সমস্যাটা কার্যত অমীমাংসিতই থেকে গিয়েছিল দীর্ঘদিন!

নিউটন, লাইবনিজ সহ আরো সব স্বনামধন্য গণিতজ্ঞরা এই ডাকে সাড়া দিয়েছিলেন। জোহানের ভাই জ্যাকবও অংশ নিয়েছিলেন। অবশ্য জোহান বার্নোলি যে নিউটনের ভয়ংকর বিরোধী ছিলেন, সেকথা নিউটনের অজানা ছিল না। ক্যালকুলাস আবিষ্কারের ক্রেডিট-টা কার পাওয়া উচিত — ইংল্যান্ডের নিউটন না জার্মানির লাইবনিজ, এই নিয়ে ভয়ংকর তর্ক-বিতর্ক চলতো তখন। এই তর্ক যুদ্ধে লাইবনিজের দিকের লোক ছিলেন বার্নোলি ভাইয়েরা।

জোহান বার্নোলির সেই চ্যালেঞ্জের উত্তরে নিউটন কিন্তু সরাসরি তাঁর সমাধান পাঠাননি। এদিকে এক প্রকাশ্য সভায় জোহান বার্নোলি নিউটনের নাম না করে পরোক্ষে তাঁকে চ্যালেঞ্জ করে বসলেন। জানা যায়, ভয়ংকর অসন্তুষ্ট নিউটন একরাত জেগে প্রশ্নটির সমাধান করেন। নিজের নাম ব্যবহার না করে Philosophical Transaction of the Royal Society পত্রিকায় তা প্রকাশ করেন তিনি।

চ্যালেঞ্জের উত্তর

বার্নোলির চ্যালেঞ্জের উত্তর দিলেন সারা ইউরোপের মাত্র পাঁচজন গণিতজ্ঞ: জোহানের ভাই জেকব বার্নোলি, ক্যালকুলাসের দুই আবিষ্কর্তা নিউটন এবং লাইবনিজ, এবং সেই সময়ের আরও দুই বিখ্যাত গণিতজ্ঞ ল’পিতাল এবং শার্নহাউস। জানা গেল, এই ব্রাকিস্টোক্রোন প্রবলেমের উত্তর অর্থাৎ সবচেয়ে কম সময়ে নেমে আসার পথের জ্যামিতিক চরিত্র হবে একটা সাইক্লয়েড।

সাইক্লয়েড অনেকটা অর্ধবৃত্তের মতই দেখতে, কিন্তু ঠিক তা নয়। গাণিতিক চেহারা একেবারে অন্যরকম। মনে করা যাক, একটা গাড়ির চাকা গড়িয়ে যাচ্ছে। চাকার উপরিতলে একটা নির্দিষ্ট বিন্দুকে লক্ষ্য করলে সেটা যে পথ অনুসরণ করবে তা হবে একটা সাইক্লয়েড।

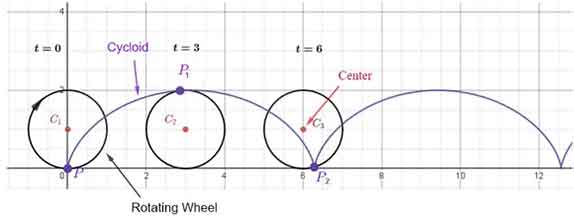
এরকম একটা সাইক্লয়েডকে উলটে দিলেই হবে ব্রাকিস্টোক্রোনের পথ। পথটা নিচের ছবিতে দেওয়া লাল রেখাটা।

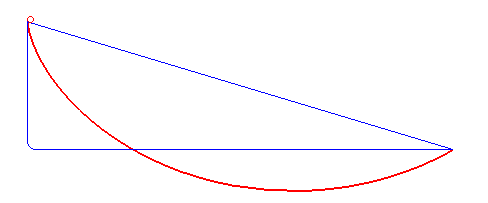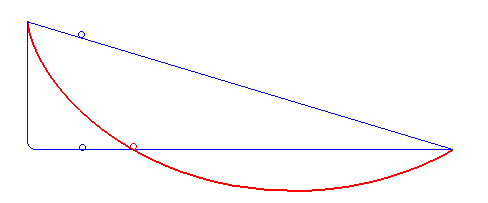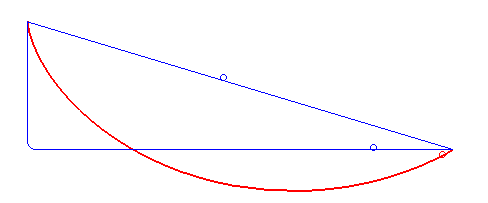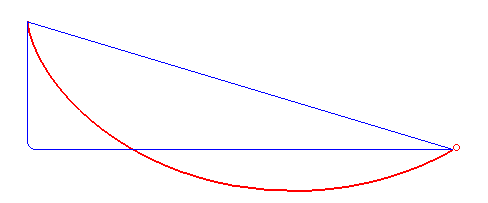
এখন বোঝা গেলো, গ্যালিলিওর ইঙ্গিত সঠিক দিশায় ছিল না, কারণ তিনি ভেবেছিলেন ব্রাকিস্টোক্রোনের পথ একটা বৃত্তের অংশ! তা হোক। প্রবলেমটা তো এসেছিল তাঁর হাত ধরেই। সাইক্লয়েড নামটাও তাঁরই দেওয়া।

এই পাঁচটা সমাধানের মধ্যে একটায় কিন্তু লেখকের নাম প্রকাশ করা হয়নি। সেই পান্ডিত্যপূর্ণ সমাধান পড়ে মনে হচ্ছিল লেখক যেন অঙ্কটা করার আগে থেকেই জানতেন যে উত্তরটা একটা সাইক্লয়েড হবে। আর, এই ধরেই তাঁর হিসাবনিকাশ। তবে, অনামী সেই লেখার মালিক যে স্বয়ং নিউটন, সেটা বুঝে গিয়েছিলেন জোহান বার্নোলি সহ আরো অনেকেই। নিউটনের সমাধান পড়ে জোহান বার্নোলি ভীষণ মুগ্ধ হয়েই মন্তব্য করেছিলেন, “পায়ের ছাপ দেখে সিংহকে বেশ চেনা যাচ্ছে!”

তবে ব্রাকিস্টোক্রোন প্রবলেমের সবচেয়ে চমৎকার সমাধান অবশ্য বার করেছিলেন যিনি চ্যালেঞ্জ ছুঁড়েছিলেন সেই জোহান বার্নোলি নিজেই! লেখার পরের পর্বে আমরা সেই চমকপ্রদ সমাধানের গল্প শুনবো।

টীকা

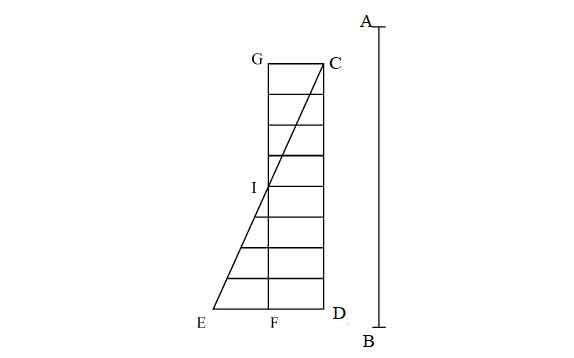
[1] এই যুক্তিপ্রয়োগের একটা ছোট উদাহরণ দেওয়া যাক। উপরের চিত্রে দেখানো হচ্ছে কোনো বস্তু $A$ বিন্দুতে স্থিতাবস্থা থেকে বিনা বাধায় নিচে পড়ছে ও শেষ অব্দি $B$ বিন্দুতে পৌঁছাচ্ছে। এখানে ঐ দূরত্ব যেতে যে সময় লাগবে, তাকে $CD$ দিয়ে নির্দেশ করা হয়েছে। এভাবে অভিকর্ষের অধীনে সুষম ত্বরণে গতিশীল ঐ বস্তুর গতি বিবেচনা করলেন গ্যালিলিও নিম্নলিখিত ভাবে:

$CD$ আসলে অসংখ্য বিন্দু দিয়ে তৈরি যার প্রতিটি বিন্দু সময়ের একটি মুহূর্তের সাথে মিলে যায়।
$AB$ যে কোনো স্বেচ্ছাধীন দূরত্ব।
$CD$ এর মধ্যে ঐ অসংখ্য সময়-বিন্দু দিয়ে অসংখ্য অনুভূমিক রেখা টানা যায়, যার কোনো একটির দৈর্ঘ্য সেই মুহূর্তে পতনশীল বস্তুটির তাৎক্ষণিক বেগের সমান ।
সুতরাং $CED$ ত্রিভুজটি হল বস্তুটি $AB$ দূরত্ব নিচে নামাকালীন তার “সমস্ত বেগের সংগ্রহ”।
$CGFD$ হল ঐ দূরত্ব নিচে নামার সময় সমবেগ অংশের প্রতিনিধি।

[2] জোহান এবং জ্যাকব এই দুই ভাই, দুইজন সুইস গণিতজ্ঞ তখন ইউরোপের উজ্জ্বল নক্ষত্র! নিউটন, লাইবনিজরা এতদিনে খানিকটা বুড়ো হয়েছেন। প্রসঙ্গত:, এই বার্নোলি ফ্যামিলি থেকে বাবা, কাকা, ছেলে, ভাইপো মিলিয়ে সাতজন নামকরা গণিতজ্ঞ উঠে এসেছেন। পরে তোমরা প্রবাহী গতিবিদ্যা (Fluid Mechanics) পড়তে গিয়ে জানবে ড্যানিয়েল বার্নোলির নাম, জোহান-এর ছেলে তিনি। ড্যানিয়েলের ঘনিষ্ঠ বন্ধু, সর্বকালের সেরা গণিতজ্ঞদের একজন অয়লার (Euler)-এর নাম হয়ত ইতিমধ্যেই শুনেছো। ড্যানিয়েলের বাবা জোহান-এর প্রিয় ছাত্র এই অয়লার।

galileo geometry gravity mathematics

লেখক পরিচিতি

অনির্বাণ ঘোষ ("বিজ্ঞান" সম্পাদক)

অনির্বাণ ঘোষ জনস হপকিন্স বিশ্ববিদ্যালয়ে তাত্ত্বিক পদার্থবিদ্যার পি এইচ ডি করেছেন। এর আগে পড়াশুনো করেছেন খড়গপুর আই আই টি থেকে। বর্তমানে MathWorks প্রযুক্তি সংস্থায় কর্মরত।

প্রদীপ্ত পঞ্চাধ্যায়ী (কাঁথি প্রভাত কুমার কলেজ)

প্রদীপ্ত পঞ্চাধ্যায়ী পশ্চিমবঙ্গের পূর্ব মেদিনীপুর জেলার কাঁথি প্রভাত কুমার কলেজের পদার্থবিদ্যা বিভাগের (UG এবং PG) অ্যাসোসিয়েট অধ্যাপক। তাঁর গবেষণার বিষয়বস্তু কোয়ান্টাম আলোকবিদ্যা এবং বিভিন্ন অর্ধপরিবাহী ডিভাইসে টানেলিং।

অভিজিৎ কর গুপ্ত (পাঁশকুড়া বনমালী কলেজ)

অভিজিৎ কর গুপ্ত পাঁশকুড়া বনমালী কলেজে পদার্থবিদ্যার গবেষক ও অধ্যাপক। ওনার গবেষণার বিষয় Computational physics। গবেষণা ছাড়াও ওনার শখ ফটোগ্রাফি। প্রকৃতি এবং সাধারণ মানুষ, দুইয়েরই ছবি তুলতে উনি খুব ভালোবাসেন।

বিজ্ঞান-এ প্রকাশিত লেখার মৌলিকত্ব, তথ্যের যথার্থতা এবং মতামত সম্পূর্ণভাবে লেখকের দায়িত্ব। লেখায় ভুলত্রুটি বা আপত্তিকর কোন বিষয় বা কপিরাইটেড ছবির অনুপযুক্ত ব্যবহার চোখে পড়লে নিচের comments-এ বা email-এ ([email protected]) জানাতে পারেন।

মন্তব্য করুন

গ্যালিলিওর শেষ জীবন: সমস্যার সূত্রপাত

ক্যালকুলাস আবিষ্কার: নিউটন ও লাইবনিজ

গ্যালিলিওর সমস্যা ক্যালকুলাসের ভাষায় কীভাবে বলবো?

বার্নোলির চ্যালেঞ্জ: নিউটন কি পারবেন ?

চ্যালেঞ্জের উত্তর

টীকা

Leave a Reply Cancel reply

সম্পূর্ণ তালিকা

লেখক তালিকা

Donate - সাহায্য করুন

চাষের জন্য কি জমি লাগে?

আইজিং মডেল : আপাত-ব্যর্থতা ও সাফল্যের গল্প

কোন ঘড়ি সবথেকে সঠিক (সময় গণনার ইতিহাস - পর্ব ৩)

ব্রাকিস্টোক্রোন সমস্যা: সমাধান ও প্রয়োগ

ব্রাকিস্টোক্রোন সমস্যা: গোড়ার কথা

Useful Links

জনপ্রিয়

নিয়মিত বিজ্ঞানের খবরাখবর পেতে তোমার ইমেইল নথিভুক্ত করো

সব লেখা (Archive)