গ্রহ যখন সূর্যের চারিদিকে চক্কর কাটছে কিংবা ইলেক্ট্রন নিউক্লিয়াস-এর চারিদিকে, তখন তাদের উপর বল-টা (force) কোনদিকে?
বৃত্তীয় গতির আলোচনার ক্ষেত্রে অভিকেন্দ্র ত্বরণ (centripetal acceleration), অভিকেন্দ্র বল (centripetal force) ও অপকেন্দ্র বলের (centrifugal force) কার্যাবলী গুলিয়ে ফেলতে দেখা যায়। নবম থেকে দ্বাদশ শ্রেণির বাংলায় লেখা প্রচুর পাঠ্য বইয়েও বৃত্তীয় গতির আলোচনায় ভুল ব্যাখ্যা দেওয়া থাকে।
সেগুলোর কথা বলার আগে আমরা বৃত্তাকার (circular) বা উপবৃত্তকার (elliptical) পথে কোনো কণা বা বস্তুর গতি ও তার কারণ সম্পর্কে আলোচনা করি।
বৃত্তীয় গতি (circular motion)
কোন বস্তু যখন বৃত্তাকার বা উপবৃত্তাকার পথে সমদ্রুতিতে (uniform speed) চলে, তখন যাত্রাপথের প্রতিটি বিন্দুতে তার বেগের দিক পরিবর্তন হয় (আগের বিন্দুর সাপেক্ষে)। কিন্তু বেগের মানের কোন পরিবর্তন হয় না। যেমন, নিচের ছবিতে অ কেন্দ্র-বিশিষ্ট একটি বৃত্তের অংশ চছ দেখানো হয়েছে। একটি বস্তু সমদ্রুতিতে এই চছ পথ বরাবর গেলে বিভিন্ন বিন্দুতে তার বেগের মান সমান কিন্তু দিক ভিন্ন হয়। সেই সমমান কিন্তু ভিন্ন দিকের বেগকে আমরা একই দৈর্ঘের ভিন্ন অভিমূখী তীরচিহ্ন দিয়ে প্রকাশ করলাম। তিনটে খুব কাছের বিন্দু ক,খ ও গ তে বেগ যথাক্রমে তীরচিহ্ন কক’, খখ’ ও গগ’ দিয়ে দেখানো হল। প্রতিটি বিন্দুতে বেগ ঐ বিন্দু ও কেন্দ্র সংযোগকারী ব্যাসার্ধের উপর লম্ব (perpendicular)।
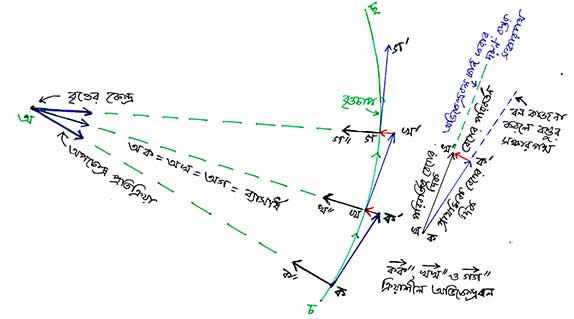
ক‘খ ও খ‘গ তীর (লাল রং) দিয়ে বস্তুর বেগের অভিমূখ আগের বিন্দুর তুলনায় কতটা ঘুরেছে, তা নির্ধারণ করা হয়েছে। নিউটনের প্রথম গতিসূত্র অনুযায়ী বস্তুটার উপর কোনো বল না থাকলে তার গতিপথ হওয়ার কথা কক‘ সরলরেখা বরাবর। কোন দিকে না ঘুরে ঐ সরলরেখা ধরে সোজা অপরিবর্তনীয় বেগে তার চলার কথা। কিন্তু তা না হয়ে সেটা ক‘-এর বদলে খ বিন্দুতে পৌঁছে গেছে। ক বিন্দুতে বস্তুটার বেগ যা ছিল আর খ বিন্দুতে যা হল, তার পার্থক্য হচ্ছে ক‘খ। ক থেকে খ–তে পৌঁছাতে যা সময় লেগেছে সেই সময়েই বেগের পরিবর্তন হয়েছে।
অভিকেন্দ্র বল (centripetal acceleration)
খেয়াল করে দেখো, ত্বরণ (acceleration) শুধু বেগের মান পরিবর্তন থেকে নয়, দিক পরিবর্তন থেকেও হয়। এক্ষেত্রে মান এক থাকলেও, দিক পরিবর্তনের কারণে সময়ের সাপেক্ষে ক‘খ অভিমূখে বেগের পরিবর্তন হয়েছে। তার মানেই সেই দিকে বস্তুটার ত্বরণ সৃষ্টি হয়েছে।
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী একটা বস্তুর ত্বরণ সৃষ্টি হয়েছে মানেই তার উপর বাইরে থেকে ক্রিয়াশীল কোন বল (external force) থাকতে হবে। এবং সেই বল উৎপন্ন ত্বরণের অভিমূখে কাজ করবে। এক্ষেত্রে ত্বরণের মতো বলের দিকটাও বৃত্তাকার পথের কেন্দ্রের দিকে। অতএব বৃত্তাকার কক্ষপথে আবর্তনশীল কণা বা বস্তুকে ঘোরাবার জন্য কেবলমাত্র কেন্দ্রের দিকে ক্রিয়াশীল একটা বলেরই প্রয়োজন হয়, অন্য কোন বলের দরকার নেই। এই বলকেই অভিকেন্দ্র বল বলা হয়।
প্রতিমুহূর্তেই এই বলটা সেই কণা বা বস্তুকে সরলরেখা থেকে বিচ্যুত করে কেন্দ্রের দিকে টানার চেষ্টা করে। যেমন, ছবিতে বস্তুটা এমনিতে ক থেকে যেত কক‘ দিশায় কিন্তু এই বলের কারণে সেটা কিছুটা কেন্দ্রের দিকে গিয়ে পৌঁছল খ বিন্দুতে। আবার খ থেকে সেটা কোনো বলের অনুপস্থিতিতে যেত খ‘-এর দিকে কিন্তু আবার সেই একই অভিকেন্দ্র বল বস্তুটাকে কেন্দ্রের দিকে টেনে গ বিন্দুতে পৌঁছে দিল।
গ্রহদের বৃত্তীয় গতি
যদি আমরা ধরি পৃথিবীসহ অনান্য গ্রহগুলো সূর্যকে বৃত্তাকার পথে আবর্তন করছে (আসলে পথটা উপবৃত্ত), সেই আবর্তনের কারণ সূর্যের মহাকর্ষ বল। গ্রহগুলোও কিন্তু সমপরিমান মহাকর্ষ বল সূর্যের উপর প্রয়োগ করে। কিন্তু সূর্যের ভর অত্যন্ত বেশি হবার ফলে সেই বলে তার কোন হেলদোল হয়না।
নিচের ছকে কয়েকটি গ্রহের জন্য ক‘খ দূরত্বটা দেখানো হল। খেয়াল রেখো, ওই দূরত্ব-টা হলো, সরলরৈখিক পথ থেকে কতটা বিচ্যুতি ঘটেছে, তার পরিমাপ।
| গ্রহ | সূর্যের কেন্দ্র থেকে দূরত্ব (106 কিমি এককে) | সূর্যকে প্রদক্ষিণ বেগ (কিমি/ সেকেন্ড) (কিমি/ঘন্টা) | এক ঘন্টায় ক‘খ দূরত্ব হবে (মিটার) |
| বুধ | 57.9 | 47.4 1,71,360 | 69.85 |
| পৃথিবী | 149.6 | 29.8 1,07,280 | 10.66 |
| বৃহস্পতি | 778.6 | 9.7 34,920 | 0.22 |
বুধ সূর্যের নিকটবর্তী হওয়ার ফলে তার ওপরে মহাকর্ষ বলের টান খুব বেশি। বুধ যদি স্থির থাকত তবে ঐ দূরত্ব থেকে সূর্যে বিলীন হতে সময লাগত মাত্র 20 দিন। কিন্তু বুধ ছুটছে, সূর্য ও বুধের সংযোগকারী ব্যাসার্ধের সাথে লম্বভাবে, ঘন্টায় 1,17,360 কিলোমিটার বেগে। এই পালানোর চেষ্টাকে আটকে সূর্যও তাকে নিজের দিকে প্রতি ঘন্টায় 69.85 মিটার টেনে নিয়ে আসছে। অর্থাৎ, এখানে পূর্বোক্ত অভিকেন্দ্র বল আসছে সূর্যের কাছ থেকে। তবে লক্ষ্য করার বিষয় হলো যে এই টানাটানি সত্ত্বেও বুধ আর সূর্যের মধ্যবর্তী দূরত্বটা কিন্তু স্থির থাকে। কারণ বুধ তার গতির ফলে কিছুটা দূরে সরে গেলেও সূর্যের টানে কাছেও আসে। তার গতি এমনই যে যতটা দূরে গেল আর যতটা কাছে এলো, দুইয়ের ভেক্টর যোগফল করার পর দেখা যায়, বুধ সূর্যের থেকে একই দূরত্বে রয়ে গেছে। তার ফল স্বরূপ কক্ষপথটা হয় বৃত্তাকার (আসলে উপবৃত্তাকার হচ্ছে কিন্তু সেই খুঁটিনাটিতে এখন গেলাম না)।
যদি ঐ দূরত্বে বুধের বেগ কমে গিয়ে পৃথিবীর বেগের সমান হতো, তাহলে এক ঘন্টায় বুধ 1,07,280 কিলোমিটার যেত। কিন্তু এক ঘন্টা পর সূর্য থেকে বুধের দূরত্ব আগের থেকে প্রায় 10,000 কিলোমিটার কম হয়ে যেত। অর্থাৎ বুধ যতটা দূরে সরে যেতে পারতো তার গতির ফলে, সূর্য তার থেকে বেশি কাছে টেনে নিতো এবং দুইয়ের ভেক্টর যোগফল করে দেখা যেত, বুধ সূর্যের আরো কাছে এসে গেছে। দূরত্ব কমে গেলে মহাকর্ষ বল বেড়ে যেত, বুধকে সূর্য নিজের দিকে আরও বেশি কাছে টেনে নিয়ে আসতো। ফলে বুধ ও সূর্যের ব্যবধান ক্রমাগত কমে গিয়ে বুধ ঘুরতে ঘুরতে সর্পিল গতিতে সূর্যে বিলীন হয়ে যেত।
আবার যদি কোনো গ্রহের বেগ হঠাৎ বেড়ে যায়, ধরা যাক পৃথিবীর বেগকে বাড়িয়ে ঘন্টায় 1,17,360 কিলোমিটার করা হল, তখন সে তার স্বাভাবিক অবস্থান থেকে এক ঘন্টায় 10,000 কিমি বেশি দূরে চলে যাবে। ফলে মহাকর্ষ বলের টান যাবে কমে, সূর্যের যতটা কাছে টানার কথা তার চেয়ে কম দূরত্ব যাবে। ধীরে ধীরে সূর্য ও পৃথিবীর দূরত্ব বাড়তে থাকবে, এক সময় পৃথিবী সূর্যের আকর্ষণ কাটিয়ে সৌরজগত থেকে মুক্তি পেয়ে যাবে।
তাহলে সূর্য আর গ্রহের ব্যাসার্ধ বরাবর সূর্যের মাধ্যাকর্ষণ বলই এখানে অভিকেন্দ্র বল হিসেবে কাজ করে এবং গ্রহটাকে বৃত্তাকার কক্ষে চালু রাখে। এটা পরমাণুর কেন্দ্রের নিউক্লিয়াস (nucleus) আবর্তনকারী ইলেক্ট্রনের ক্ষেত্রেও সমানভাবে প্রযোজ্য। এখানে কেন্দ্রের নিউক্লিয়াস ও ইলেক্ট্রনের মধ্যে ক্রিয়াশীল মহাকর্ষ বল ওগুলোর মধ্যে কার্যকরী স্থির-তড়িৎ বলের তুলনায় খুবই নিষ্প্রভ। সুতরাং ঐখানে অভিকেন্দ্র বল হিসাবে স্থির-তড়িৎ বল কাজ করে, সেই বল কেবলমাত্র ইলেক্ট্রন-এর বেগের দিক পরিবর্তন করে চলে। সেজন্য ইলেনকট্রন গ্রহের মতন নির্দিষ্ট ব্যাসার্ধ-বিশিষ্ট বৃত্তাকার কক্ষপথে নির্দিষ্ট বেগসহ নিউক্লিয়াসকে আবর্তন করে। এজন্য আর অন্য কোন বলের প্রয়োজন হয় না।
এবার শুরুর কথায় আসা যাক। বাংলা মাধ্যমের বেশ কিছু বইয়ে পরমাণু-র নিউক্লিয়াস-এর চারিধারে ইলেক্ট্রনের গতি সম্পর্কে যা আলোচনা করা হয়েছে, তার একটা নমুনা পেশ করা যাক।
গন্ডোগোলের শুরু
এই ব্যাখ্যায় অভিকেন্দ্র বলের কোন উল্লেখ নেই, অথচ অপকেন্দ্র বলকে নিয়ে আসা হয়েছে। দ্বাদশ শ্রেণীর রসায়ন বইগুলোতেও একইভাবে ব্যাখ্যা করা হয়েছে। অনেক শিক্ষক ও শিক্ষিকা ক্লাসে এবং এই লক-ডাউনে অন-লাইন ক্লাসে দূরদর্শনের পর্দায় এই ব্যাখ্যা দিয়ে যাচ্ছেন। এতে ছাত্রছাত্রীরা অত্যন্ত ভুল শিখতে পারে, যা শোধরাতে বেগ পেতে হবে।
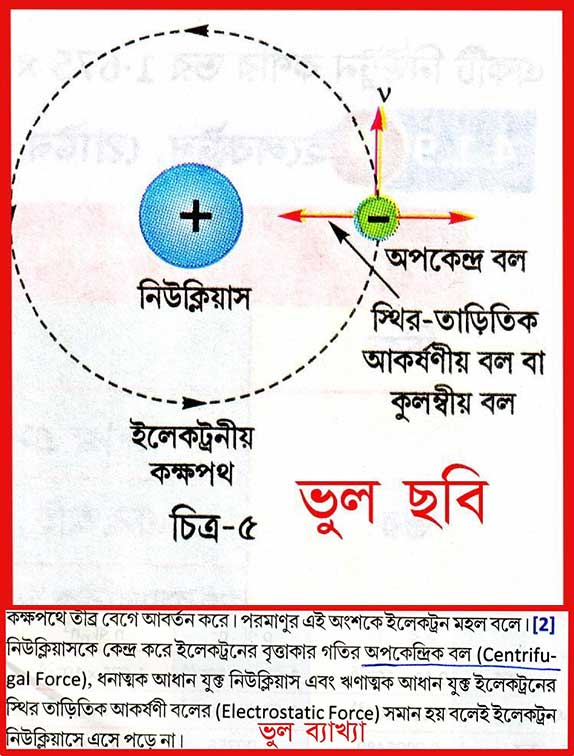
অভিকেন্দ্র বল ও অপকেন্দ্র প্রতিক্রিয়া
অভিকেন্দ্র বল রূপে গ্রহগুলোর উপর সূর্যের মহাকর্ষ বল ও ইলেক্ট্রনের উপর স্থির-তড়িৎ বল হচ্ছে একটি বস্তু দ্বারা অন্য বস্তুর উপর ক্রিয়া বল এবং বাস্তব বল। তাহলে নিউটনের তৃতীয় গতিসূত্র অনুযায়ী এর প্রতিক্রিয়া বল থাকবেই, সেটা গ্রহগুলো সূর্যের ওপর ও ইলেক্ট্রন নিউক্লিয়াস-এর উপর প্রয়োগ করবে। সেটা অভিকেন্দ্র বলের বিপরীত হবে ও একই সরলরেখায় কাজ করবে। এই প্রতিক্রিয়া বলকে অপকেন্দ্র প্রতিক্রিয়া বলে।
অভিকেন্দ্র বল ও অপকেন্দ্র প্রতিক্রিয়া হল এক জোড়া ক্রিয়া-প্রতিক্রিয়া বল, একসঙ্গে উপস্থিত থাকে। মনে করুন আপনি একটা ঢিলকে সুতোয় বেঁধে সুতোটার অন্যদিকে একটা বড় ফাঁস দিলেন, যার মধ্যে দিয়ে আপনার তর্জনী সহজেই গলে যায় এবং ফাঁসটা আঙ্গুলে ঢিলে হয়ে থাকে। এবার আপনি হাতের কব্জি ঘুরিয়ে ঢিলটাকে অনুভূমিক তলে ঘোরাতে থাকুন। এই ভাবে ঘোরানোর জন্য আপনি ঢিলটার ওপর যে বল দিচ্ছেন তা হল অভিকেন্দ্র বল। লক্ষ্য করুন, আপনার তর্জনীতে সুতোর টান অনুভুত হচ্ছে, ঢিল আপনার তর্জনীর ওপর একটা বল প্রয়োগ করছে, সেটা হল অপকেন্দ্র প্রতিক্রিয়া। সাধারণ সুতোর বদলে মাঞ্জা সুতো নিলে অভিজ্ঞতা আরো ভয়ানক হবে, আঙ্গুল কেটে যাবে!!!
অপকেন্দ্র বল
অপকেন্দ্র প্রতিক্রিয়া কিন্তু অপকেন্দ্র বল নয়, অপকেন্দ্র বল একটা অলীক বল। যে বলের কোন বাস্তব অস্তিত্ব নেই কিন্তু ত্বরণযুক্ত পরিবেশে কোন ঘটনাকে ব্যাখ্যা করার জন্য একে আমদানী করতে হয়। ধরুন আপনি ঘন্টায় 60 কিলোমিটার বেগে যাচ্ছে এমন কোন বাসের সীটে বসে আছেন, সীট ও আপনার উভয়ের বেগ সমান। এই বাস ও আপনার বেগ এখন কত তা বাসের ভেতর থেকে আপনি মাপতে পারবেন না কেননা বাসের সাপেক্ষে আপনি স্থির। রাস্তার উপর দাঁড়িয়ে থাকা কেউ সেটা মাপতে পারবে; ছেলেবেলার অঙ্কের কথা মনে করুন, 20 মিটার লম্বা একটা বাস 5 সেকেন্ডে একটা খুঁটি অতিক্রম করলে বাসের বেগ কত? হঠাৎ বাসটা ব্রেক কষে বেগ ঘন্টায় 15 কিলোমিটারে নামিয়ে আনল, আপনি সামনের সীটে ছিটকে পড়লেন। কেন এমন হল?
রাস্তায় দাঁড়িয়ে যিনি বাসের বেগ মাপছিলেন, তিনি বলবেন বাসটার বেগ কমলেও আপনার বেগ একই আছে তাই আপনি নিজের গতি বজায় রাখতে সীট ছেড়ে এগিয়ে চলে গেলেন। গতিশীল বস্তুর এই স্বভাবকে গতি জাড্য (intertia) বলে। কিন্তু আপনি ভাবলেন, আমি ও বাস পরস্পরের কাছে স্থির ছিলাম, না আমি সীট ছেড়ে চলে যাচ্ছিলাম না সীট আমাকে ছেড়ে চলে যাচ্ছিল। সীট নিশ্চয়ই আমাকে ছুঁড়ে ফেলার জন্য একটা বল প্রয়োগ করেছে। এই আপনি ঘটনাটা ব্যাখ্যা করার জন্য একটা বল জোগাড় করলেন, সেটা হল অলীক বল। ত্বরণ (acceleration) বা মন্দন (retardation) যুক্ত পরিবেশে, পদার্থ বিজ্ঞানের ভাষায় ত্বরিত নির্দেশ ফ্রেমে (noninertial frame of reference), ত্বরণের বিপরীতে উদ্ভূত ঘটনার ব্যাখ্যার জন্য এই বলটাকে লাগে।
এবার পরিবেশ বা ফ্রেম-টা যদি সরলরেখায় ত্বরণশীল না হয়ে বৃত্তীয় গতিতে চলে, তার উপর কেন্দ্রের দিকে সর্বদা অভিকেন্দ্র ত্বরণ থাকে (একটু আগেই যেটা দেখলাম)। সেজন্য এই ফ্রেমের ভেতরে অবস্থিত বস্তু কেন্দ্রের বিপরীত দিকে ব্যাসার্ধ বরাবর ছিটকে যায়। অভিকেন্দ্র বল সব সময় কাজ করে বলে ফ্রেমটা ঘোরে আর এর ভেতরে থাকা বস্তুও বাইরের দিকে ছিটকে যায়। অভিকেন্দ্র বল আর অপকেন্দ্র বল কখনই পরস্পরকে প্রশমিত করতে পারেনা।
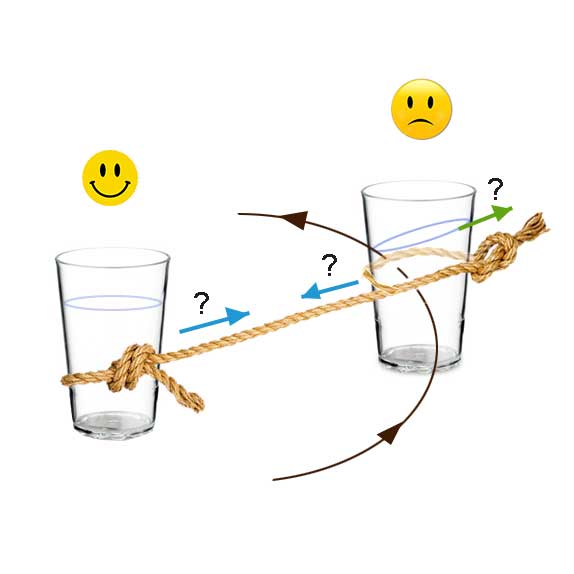
আগের পরীক্ষার মতন ঢিলের বদলে একটা প্লাস্টিকের গেলাসে তলায় একটা সূক্ষ ছিদ্র করে এতে জল ভর্তি করে সেটা সুতোর সাহায্যে ঘোরাতে থাকুন। দেখবেন আপনার অভিকেন্দ্র বলের প্রয়োগে গেলাসটা (নির্দেশ ফ্রেম) ঘুরছে। আপনার ব্যাখ্যায় গতি জাড্যের জন্য কিন্তু জলের ব্যাখ্যায় অপকেন্দ্র বলের ফলে গেলাসের মধ্যের সব জল (ত্বরিত ফ্রেমে বস্তু) ফুটো দিয়ে বেরিয়ে যাচ্ছে। এরা পরস্পরকে প্রশমিত করছে না, কারণ অভিকেন্দ্র বল বাস্তব বল কিন্তু অপকেন্দ্র বল অলীক বল।
শেষের কথা ছবিতে ব্যাখ্যা ধরে আরেকটা কথা বলা যায়, যদি স্থির-তড়িৎ বল ও অপকেন্দ্র বল পরস্পরকে প্রশমিত করে তবে ইলেক্ট্রনের ওপর মোট বল শূণ্য। নিউটনের প্রথম গতি সূত্র অনুযায়ী ইলেক্ট্রনটা স্বাধীনভাবে সরলরৈখিক পথে সমদ্রুতিতে চলতে থাকবে। এখন সেটা কিভাবে কেন্দ্রীনের চারিদিকে আবর্তিত হবে? এই ব্যাখ্যা অনুযায়ী কোন ইলেক্ট্রনই নিউক্লিয়াস-এর চারিদিকে ঘুরবে না। সঠিক ছবিটা দিয়ে আলোচনার ইতি টানা যাক।
প্রথম ও দ্বিতীয় ছবি লেখকের আঁকা, তৃতীয়, চতুর্থ ছবি দশম শ্রেণির বিভিন্ন পাঠ্য বইয়ে আঁকা ছবি।

very easily and clearly understandable.