কম্পিউটার কি কি কাজ পারে, আর কি কি কাজ পারে না, সে এক গভীর প্রশ্ন। তার উত্তর খুঁজতে পাড়ি দিতে হবে অঙ্ক ও যুক্তির এক মজার জগতে।
শুরু করা যাক ছোটবেলায় শেখা অঙ্ক দিয়ে।
আমরা গুণ করতে সকলেই শিখেছি। ধরো তোমাকে ৩১ আর ৮৯ — এই দুই সংখ্যার গুণফল নির্ণয় করতে বললাম। কাগজ কলম নিয়ে বসলে গুণটা করতে পাঁচ মিনিটও লাগবে না। ক্যালকুলেটরে করলে তো কথাই নেই, বোতাম টিপলেই উত্তর।
শুধু এই দুটি সংখ্যা কেন? যেকোনো দুটি সংখ্যা গুণ করাই খুব সোজা। এক হয় হাতে হাতে করা — ইশকুলে শেখানো পদ্ধতিতে। তবে খুব বড় সংখ্যা হলে কিন্তু সমস্যা! কেসি নাগের বইয়ের বিভিন্ন অঙ্কের লেজুড় সেই ইয়া বড় গুণগুলো মনে আছে? মাধ্যমিকের আগে পরীক্ষার হলে ক্যালকুলেটর ব্যাবহার করা যেত না। ওগুলো হাতে করতে কোনও না কোনও সময় হিমসিম খেতেই হয়েছে! কিন্তু এগারো ক্লাস থেকে এলো ক্যালকুলেটর। অত্যধিক বড় সংখ্যা না হলে ক্যালকুলেটরে টিপতে সাথে সাথেই উত্তর। তখন ফিজিক্স, কেমিস্ট্রি, অঙ্কের মোটা মোটা বই, শক্ত শক্ত কন্সেপ্ট। হাতে ধরে এত গুণ করার সময় কই? এদিকে প্রায় সব অঙ্কেই কত সংখ্যা যে গুণ করতে হবে তার ইয়ত্তা নেই! সেসব সংখ্যা আবার দেখতে ভয়াল — ডেসিমালের পর পাঁচ ছয় ঘর ধরে চলতেই থাকে। দত্ত-পালের ফিজিক্সের বইয়ের বা মাইতি-তিওয়ারির ফিজিক্যাল কেমিস্ট্রির বই — সবই ওরকম ভজঘট ভ্যালু দেওয়া অঙ্কে ঠাসা। সবেতেই ভরসা ক্যালকুলেটর বাবাজি।
প্রসঙ্গে ফিরি। গুণ তো হল। কিন্তু যদি একটু ঘুরিয়ে দি প্রশ্নটা? তুমি ধর দিব্বি ভাল মুডে আছ একদিন, হটাৎ আমি বললাম ২৭৫৯ দুটি মৌলিক সংখ্যার গুণফল — সেই সংখ্যা দুটি বের করে দেখাও দেখি। অমনি তুমি জব্দ — মেজাজ ঘেঁটে একশা। আর সহজে কাগজে কলমে করার উপায় নেই। দিনরাত এক করে খাতা-পেন্সিল নিয়ে বসে ১ থােক ২৭৫৯ অবধি সবকটা সংখ্যা লিখে কোনটা ২৭৫৯ দিয়ে ভাগ যাচ্ছে টেস্ট করতে না চাইলে একটাই উপায়। কম্পিউটার খুলে C বা Java তে প্রোগ্রাম লেখা। যেকোনো algorithm ক্লাসে শেখানো হয় এরকম একটি প্রোগ্রাম – ১ থেকে শুরু করে ২৭৫৯ এর বর্গমূল অবধি সংখ্যাগুলির কোনও একটি দিয়ে ২৭৫৯ ভাগ যাচ্ছে কিনা ক্রমাগত পরীক্ষা করা।
সংখ্যার এই যে নানান মজার বৈশিষ্ট্য, অঙ্কশাস্ত্রে এগুলি বের করা ও চর্চার যে পদ্ধতি, তাকে নাম্বার থিওরি বলে। তা দিয়ে দেখানো যায় যে যদি কোনও সংখ্যা নিজে মৌলিক না হয়, তার বর্গমূলের চেয়ে ছোট কোনও একটি মৌলিক সংখ্যা দিয়ে সে ভাগ যাবেই। যেহেতু ২৭৫৯ দুটি মৌলিক সংখ্যার গুণফল, একটি বেরলে অন্যটি বের করতে শুধু ২৭৫৯ কে সেই মৌলিক সংখ্যাটি দিয়ে ভাগ করলেই হবে৷ তবে এত খেটেখুটে program লিখে যা পাব তা কিন্তু বেশ আশ্চর্যের। ২৭৫৯ যাদের গুণফল সেই সংখ্যাদুটি ৩১ আর ৮৯!
এ কীরকম হল? সংখ্যাটা অপরিবর্তিত, তার মৌলিক উৎপাদক দুটিও অপরিবর্তিত। কিন্তু গুণ করা যতটা সোজা, উৎপাদকে বিশ্লেষণ করা ততটাই শক্ত! তুমি বলবে “শক্ত” কই? খেটে program লিখতে হল বটে, কিন্তু কম্পিউটার যে দিব্বি করে দিল! উত্তর হল ২৭৫৯ বলে পেরেছে, কারণ সংখ্যাটি আজকালকার কম্পিউটারের ক্ষমতার সাপেক্ষে বেশ ছোট। কিন্তু যদি সংখ্যাটি ক্রমেই বাড়াতে থাকি?
একটু খোলসা করা যাক।
আমরা জানি ডিজিটাল কম্পিউটার চলে বাইনারি সিস্টেমে — যা ইনপুট দি, তাকে প্রসেসরে পাঠানোর আগে ০ আর ১ দিয়ে প্রকাশ করতে হয় । ভেতরের সার্কিট দিয়ে বাইনারিতে রূপান্তরিত করাটা স্বয়ংক্রিয় ভাবেই হয়। এই যেমন ২৭৫৯ — বাইনারিতে ১০১০১১০০০১১১, ১২ টা বাইনারি ডিজিট দিয়ে লেখা। ধর এরম ১০০০ টা ডিজিট আছে; এমন নাম্বার লেখা আজকের যুগের সুপারফাস্ট কম্পিউটারদের কাছে জলভাত।
কিন্তু দেখানো যায় যে আমাদের আগের algorithm দিয়ে এরকম সংখ্যার মৌলিক উৎপাদক বের করতে যা সময় লাগবে তা মহাবিশ্বের বিগ ব্যাং থেকে আজ অবধি যা সময় অতিক্রান্ত হয়েছে তার থেকেও বেশি! তুমি তাও বলবে ধুস, এ তো algorithm এর দোষ। কোনও ভাল প্রোগ্রামার কোনও না কোনও ভাবে ঠিকঠাক algorithm লিখে আরামসে উত্তর বের করে দেবে, তা সে ১২ টা ডিজিট হোক বা ১০০০।
কিন্তু না, তাবড় বিজ্ঞানীরাও উৎপাদক বিশ্লেষণ করতে গিয়ে হোঁচট খান — এরকম কোনও algorithm আজ অবধি কারও জানা নেই যে! বুদ্ধি খাটিয়ে কম্পিউটার বাবাজী কে একটু তাড়াতাড়ি কাজ করানো যায় বটে — কিন্তু তাতে লাভ হয় যৎসামান্যই। মুশকিল তাহলে আরো গভীরে কোথাও!
আধুনিক কম্পিউটারের জনক Alan Turing কে প্রশ্নটি বেশ ভাবিয়েছিল। আমরাও প্রশ্নটি ভাবব, তবে তার আগে কিছু জিনিস ঠিকমত বোঝা খুব জরুরি।
প্রথমে বুঝতে হবে শক্ত কাহারে কয়। যা ক্যালকুলেটরের জন্য খুব শক্ত, এই যেমন ২৭৫৯ কে উৎপাদকে ভাঙা, তা কিন্তু ভাঙাচোরা আদ্দিকালের কোনও কম্পিউটারও সহজেই করে দেবে।
কম্পিউটার শব্দটাও বেশ গোলমেলে। কম্পিউটার মানে অনেকের কাছেই যে ছবিটা ফুটে ওঠে তা টেবিলে রাখা একটা মনিটর — সাথে মাউস, কীবোর্ড, সিপিউ। কিন্তু এটাই যে একমাত্র মডেল হতে পারে, তা কে বলে দিল?
কম্পিউটারের মূল কাজ কোনও কিছু গণনা করা — তা করা হয় সিপিউর খোলের ভেতরের microprocessor বলে যন্ত্রটি দিয়ে। কিন্তু ওরম microprocessor ফ্রিজ, টিভি, মাইক্রোওয়েভ ওভেন — সবেতেই আছে; যন্ত্রের উপর নির্ভর করে আলাদা আলাদা কাজে ব্যবহৃত হয়।
ঠিকঠাক কিছু থিওরি খাড়া করার আগে তাই সব গরুকে এক ঘাটে জল খাওয়াতে হবে। অতঃপর Turing একটা কাল্পনিক যন্ত্র ডিফাইন করলেন। নাম Turing machine। খুব সহজ সরল যন্ত্র। একটা অসীম লম্বা টেপ থাকবে – তাতে চৌকো চৌকো খোপ, কয়েকটা খোপে আগে থাকতে কিছু ইনপুট চিহ্ন আঁকা, যেমন ধরো ০ কিংবা ১। একটা “টেপ হেড” থাকবে, কোনও একটি খোপে নির্দেশ করে। টেপ হেডটা জোড়া একটা কট্রোল ডিডাইসের সাথে — সেই ডিভাইসের বেশ কয়েকটা অভ্যন্তরীণ অবস্থা বা স্টেট থাকতে পারে। বর্তমান অবস্থা (স্টেট) আর চিহ্নের ওপর নির্ভর করে মেশিনটি টেপে নতুন কোনও চিহ্ন আঁকতে পারে; আঁকার পরে টেপের ডানদিকে বা বাঁদিকে সরে যেতে পারে; আবার এর কিছুই না করে অভ্যন্তরীণ স্টেটটাই পরিবর্তন করতে পারে। বিশদে জানতে Turing এর আসল পেপারটা পড়ে দেখতে পারো। [1]
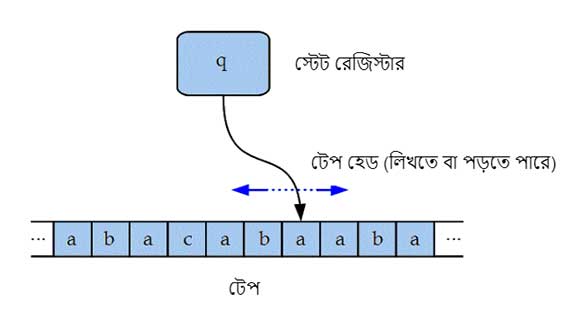
Turing machine এর একটা ছবি [3] জুড়ে দিলাম। এখানে মেশিনটির বর্তমান স্টেট বা অবস্থা “স্টেট রেজিস্টারে” দেখা যাচ্ছে। একটা টেপ হেড আছে, যেটা টেপের কোনও একটা জায়গাকে নির্দেশ করছে। টেপটিতে বিভিন্ন ইনপুট চিহ্ন আঁকা।
কি কি চিহ্ন থাকবে, কি কি স্টেট থাকবে, কখন কিভাবে টেপ হেড সরবে — এ সবই ডিজাইন প্যারামিটার, আগে থেকে ঠিক করা। স্টেট, টেপের চৌকে কি লেখা আছে, আর টেপ হেড কি করতে চায় — এই তিনটে নির্ধারণ করে মেশিনের এর বর্তমান কনফিগারেশন। এরম প্রচুর unique কনফিগারেশন হতে পারে!
শুনতে খুব সহজ লাগছে? এর ক্ষমতা কিন্তু অপরিসীম। একটু ভাবলেই দেখা যাবে,
মেশিনের বর্ণনা যতই সহজ হোক, এই মেশিন যে কোনও ডিজিটাল কম্পিউটারকে বর্ণনা করার ক্ষমতা রাখে! টেপের চিহ্নগুলি রাইনারি অ্যালফাবেটের ০ আর ১ এ সীমিত রেখে ডিজাইন প্যারামিটারগুলি ঠিকমত সেট করলেই হল।
বিজ্ঞানী Church আর Turing একধাপ ওপরে গেলেন। তাদের মতে শুধু কম্পিউটার কেন, মহাবিশ্বের যে কোনও computing device কেই simulate করার ক্ষমতা রাখে এই Turing machine! simulate বলতে সোজা কথায় অনুকরণ করা – একটা ক্যালকুলেটরের পুঙ্খানুপুঙ্খ অনুকরণ যেমন একটা কম্পিউটার দিয়ে করা সম্ভব।
সময় কম বেশি লাগতে পারে, মেমরি কম বেশি লাগতে পারে (সে প্রসঙ্গে একটু পরেই আসছি) — কিন্তু শেষমেশ simulate করতে পারবেই। এই কথাটির কিন্তু কোনও প্রমাণ নেই — গোদা ভাষায় একে বলে hypothesis। তবে এও সত্যি যে আজ অবধি এরকম কোনও যন্ত্র আবিষ্কৃত হয়নি যা hypothesis কে ভুল প্রমাণিত করে। যদ্দিন না হচ্ছে, Turing machine কেই কম্পিউটেশনের থিওরেটিক্যাল মডেল হিসেবে ধরে বিজ্ঞানীরা যাবতীয় কাজকর্ম করেন।
অনেকে আরও এক কাঠি ওপরে উঠে আরও একটু কড়া ডোজের hypothesis করেন। তাঁদের মতে মহাবিশ্বে যা efficiently computable (মানে সহজভাবে গণনা করা যায়), সবই Turing machine দিয়েও efficiently computable। কিন্তু efficiency মাপা হবে কিভাবে?
উত্তর মেমোরি আর সময় দিয়ে ।
মেমরির একক চৌকো খোপগুলি — কিছু compute করার সময় যতগুলো একক খোপে টেপ হেড সরছে, ততটাই মেশিনের মেমরির ব্যবহার।
সময়ের একক কনফিগারেশন — একটা unique কনফিগারেশন থেকে অন্য একটি একক কনফিগারেশনে যেতে যা সময় অতিক্রান্ত, তা এক ইউনিট সময়।
ডেফিনেশানে আসি। ইনপুট এনকোড করতে ধরলাম n টা বাইনারি অঙ্ক (digit) লাগছে। মেশিন efficient তখনই যখন computation শেষ করতে মেমরি আর সময় যা লাগছে তা n এর কোনও polynomial বা বহুপদ দিয়ে মাপা যায়। যত বড় polynomialই হোক না কেন — n২ বা n১000 — যাহা বাহান্ন তাহা তিপান্ন! আমরা polynomial হলেই খুশি। আরো একটু বিশদে জানার জন্য নিচে একটি লিঙ্ক দিলাম [2]।
Efficiency যেই মাপা গেল, দু ধরনের `সমস্যার’ (বা complexity class) সাথে চেনা হয়ে যাক। এদের অন্য রূপে আমরা আগে দেখেছি। প্রথম ধরনের সমস্যা এরকম polynomial সময়ে সমাধান করা যায়। এদের দ্বারা তৈরি ক্লাসটিকে বলা হয় PTIME বা P। এই যেমন দুটি সংখ্যার গুণফল — সে ছোট হোক বা বড়!
অন্য ধরণের প্রব্লেম এখনো অবধি polynomial সময়ে সমাধান করা যায় না — এই যেমন উৎপাদকে বিশ্লেষণ। কিন্তু প্রব্লেমগুলির একটা বিশেষত্ব আছে। এরম কোনও প্রব্লেমের সমাধান কেউ করে দিলে তুমি সমাধানটা ঠিক না ভুল polynomial সময়ে যাচাই করে দেখে নিতে পারবে। এদের ক্লাসকে বলা হয় NP। গালভরা নাম Non—Deterministic polynomial time — কেন সেসবে পরে একদিন আসা যাবে।
উদাহরণ দি। এই যেমন ধর কেউ ২৭৫৯ সংখ্যাটি দিয়ে বলল এর মৌলিক উৎপাদক ৩১ এর ৮৯। তুমি দিব্বি গুণ করে দেখে নিলে ৩১ এর ৮৯ এর গুণফল আদপে ২৭৫৯ কিনা । প্রশ্ন আসবে ৩১ বা ৮৯ মৌলিক সংখ্যা কে বলে দিল? তাও polynomial সময়েই যাচাই করে নেওয়া যায়, কিভাবে সেই আলোচনা পরে একদিন হবে। ছোট্ট গল্প — কোনও সংখ্যা মৌলিক কিনা তা বের করতে যে বিশ্বখ্যাত AKS algorithm ব্যবহৃত হয়, তা আবিষ্কার করেছিলেন তিনজন ভারতীয়।
একটু ভাবলেই দেখবে সব P প্রব্লেমই আসলে NP।
ধর তোমাকে ৩১ এর ৮৯ গুণ করতে দিলাম, সমাধানও দিলাম ২৭৫৯। আমার সমাধান ঠিক না ভুল যাচাই করতে কি করবে? গুণটা নিজে করে দেখবে! যেহেতু গুণ করতে polynomial সময় লাগে, সমাধানটা যাচাই করতেও polynomial সময়ই লাগবে।
উলটোদিকটাও কি সত্যি? যার সমাধান দেওয়া থাকলে polynomial সময়ে দিব্বি যাচাই করতে পার, তাকে কি polynomial সময়ে সমাধান করতে পার না? খুব সরল প্রশ্ন!
কিন্তু মজার ব্যাপার, এর উত্তর কেউ জানে না ! এটি সর্বকালের শ্রেষ্ঠ অমীমাংসিত সমস্যাগুলির মধ্যে অন্যতম । কেউ উত্তর দিতে পারলে সে পাবে Clay Mathematics Institute থেকে এক মিলিয়ন ডলার।
আচ্ছা,পাতালঘরের মতো কল্পবিজ্ঞানের সিনেমা তো তোমরা অনেকেই দেখেছ। কত হরেক রকম যন্ত্র ছিল সেখানে, সবই বিজ্ঞানের উপহার। আর এখন তো artificial intelligence এরই যুগ। অনেক AI skeptic ভয় পান যে একদিন যন্ত্র বা মেশিন সর্বেসর্বা হয়ে মানুষের ওপর ছড়ি ঘোরাবে।
এরম কি কখনো হতে পারে? এই যে আমরা মানুষ, আমরা মেশিনের থেকে ঠিক কিভাবে আলাদা? মেশিন কি কোনদিন মানুষ হতে পারে? মানুষ হওয়া মানেই বা কি? মানুষের জ্ঞানের স্বরূপই বা কি? আমরা এই যে কবিতা লিখি, ভাল ছবি দেখলে বা ভাল গান শুনলে খুশি হই, এরকম মেশিন পারবে? এরম প্রচুর প্রশ্ন ছড়িয়ে ছিটিয়ে আছে biology, philosophy, economics ও আরও কত বিষয়ে! ভাবলে অবাক হবে এ সবের গোড়াতে P vs NP। কীভাবে? পরবর্তী প্রবন্ধগুলিতে ক্রমশ প্রকাশ্য!
আর একটি মজার ব্যাপার। এই যে Church—Turing hypothesis এর কড়া ভার্সন, যাকে বলে Extended Church—Turing hypothesis, এটি কিন্তু মোটেই সত্যি না। বিজ্ঞানী পিটার শর ১৯৯8 সালে দেখান যে (কোয়ান্টাম কম্পিউটার নামক এক আজব কম্পিউটারে কিছু স্পেশাল NP problem দিব্বি efficiently polynomial সময়ে সমাধান করা যায় — Turing machine দিয়ে যা কখনওই সম্ভব না।
কোয়ান্টাম কম্পিউটারের জন্য নতুন এক complexity class তৈরি করে অনেক কিছু কেঁচে গণ্ডূষ করতে হয় । সেসব নিয়েও আলোচনা হবে। তবে হ্যাঁ, Turing machine যা একেবারেই পারে না — efficiently হোক বা না হোক — তা কিন্তু কোয়ান্টাম কম্পিউটারের দ্বারাও পারা সম্ভব না। তাই মূল Church—Turing hypothesis এখনো অক্ষত।
কোয়ান্টাম কম্পিউটার সুদূর ভবিষ্যতে তাও তৈরি করা সম্ভব বলে মানা হয় — অনেকে তৈরি করার প্রচুর চেষ্টা চালিয়ে যাচ্ছেন। দুর্জনে কিন্তু আরও এলাহি সব কম্পিউটারের কথা বলে — যা তৈরি করা
দূর অস্ত, ভারতেও বেকুব হতে হয় । অনেকেই Time machine এর গল্প পড়েছ নিশ্চয়ই।। যদি ওরম এক Time Machine থাকত? সাথে থাকত কোয়ান্টাম কম্পিউটারও৷ ভাবছ যা ইচ্ছে তাই করা যেত? গুলি মারি Church-Turing কে! না কিন্তু। অঙ্ক কষে দেখানো যায় যে তখনো Church Turing hypothesis এর থেকে বেরোনোর কোনও উপায় নেই। এরকম অতিবাস্তব জগতে বাস্তবের অপেক্ষা খুব কিছু বেশি যে করা যাবে, এমনটাও না! সেসবের কথা পরে হবে। কিন্তু এরকম শুনে ভীষণ অবাক হচ্ছো নিশ্চয়ই? ওয়েলকাম টু দ্যা ওয়ার্ল্ড অফ complexity theory!
References:
- Alan Turing. “On Computable Numbers, with an Application to the Entscheidungsproblem”, Proceedings of the London Mathematical Society, Volume s2-42, Issue 1, 1937, Pages 230–265
- Alan Cobham. “The intrinsic computational difficulty of functions.” Logic, methodology and philosophy of science, Proceedings of the 1964 International Congress, edited by Yehoshua Bar-Hillel, Studies in logic and the foundations of mathematics, North-Holland Publishing Company, Amsterdam1965, pp. 24–30.
- https://gyires.inf.unideb.hu/GyBITT/26/ch04.html
(প্রচ্ছদের ছবির সূত্র, কৃতজ্ঞতা: http://tosya.magdalene-project.org/turing-machine/)

very interesting