ধাঁধার উত্তর
১. ধাঁধা: গলিগনের খোঁজ (১৪-ই জুন, ২০১৫)
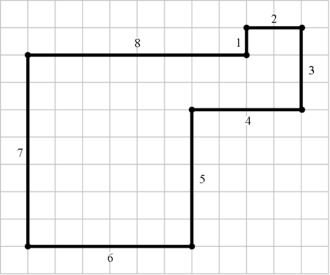
এক কথায়, উত্তর হল: হ্যাঁ, তিনি পারবেন। আর তার পথটা হবে ঠিক উপরের ছবির মত। ছবিটাতে, যদি ধরি (০,০) থেকে যাত্রা শুরু, তাহলে ওই আট বাহুযুক্ত গলিগনটাকে প্রকাশ করা যায় নীচের স্থানাংকের দ্বারা–
(০,০), (০,১), (২,১), (২,-২), (-২,-২), (-২,-৭), (-৮,-৭), (-৮,০), (০,০)
এবার সমাধানটা একটু ভেঙ্গে বলি। x-অক্ষ বরাবর যদি বিজোড় সংখ্যক দূরত্ব গুলি নিই, তাহলে y-অক্ষ বরাবর থাকবে জোড় সংখ্যক দূরত্ব গুলি। x-অক্ষ বরাবর ১,৩,৫,৭,… আর y-অক্ষ বরাবর ২,৪,৬,… ইত্যাদি। যেহেতু প্রফেসর ক্যালকুলাস আবার সেই শুরুর বিন্দুতে ফিরে আসবে, তাই ১,৩,৫,৭,… ও ২,৪,৬,…, এর মাঝে + আথবা – বসিয়ে ০ করতে হবে। + ১ – ৩ – ৫ + ৭ = ০ আর + ২ – ৪ – ৬ + ৮ = ০, এই সিকোয়েন্স নিলে পথটা পাওয়া যায়।
অবশ্য, শুধু একটা নয়, এরকম অসংখ্য পথ পাওয়া যাবে। প্রতিবারই বাহু সংখ্যা হবে ৮ এর সরল গুনিতক। কারণ এরা এমন পূর্ণসংখ্যা n যার জন্য + কি – উপযুক্ত জায়গায় বসিয়ে এই সমীকরণটা খাটে:
± ১ ± ৩ ± ৫ ± … ± (n-১) = 0
± ২ ± ৪ ± … ± n = 0
নীচে একটা ১৬ বাহু-ওয়ালা গলিগনের ছবি দেওয়া হল। ১৬টা বাহু আছে, এমন গলিগন তৈরী করা যায় ২৮ ভাবে। নীচের যে তিনটে ছবি দেওয়া হল, সেগুলোর বাহু পরস্পরকে ছেদ করবে না। কিন্তু বাকি ২৫টার বাহু পরস্পরকে ছেদ করবে।
ছবি: উইকিপিডিয়া