শূন্য (দ্বিতীয় পর্ব)

পার্থসারথি মুখোপাধ্যায়

(Narendrapur Ramkrishna Mission College)

 

25 May 2018

Link: https://bigyan.org.in/zero-02

প্রাচীন মায়া সভ্যতায় শূন্যের ধারণা

শূন্যের কথা বলতে হলে যে সভ্যতাকে এড়িয়ে কথা বলা যাবেনা, সেই প্রাচীন সভ্যতার বিকাশ হয়েছিল খ্রিস্টপূর্ব তৃতীয় শতাব্দী থেকে খ্রিষ্টীয় নবম শতাব্দীর মধ্যে বর্তমান মেক্সিকো এবং গুয়াতেমালার গভীর জঙ্গলে ঢাকা এক অঞ্চলে, পরিভাষায় যার নাম ইউকাতান পেনিনসুলা। খোলা চোখে দেখা আকাশের নক্ষত্র সমাবেশকে ভিত্তি করে একের পর এক অসাধারণ গণিতবোধসম্পৃক্ত পঞ্জিকা বা ক্যালেন্ডার তৈরি করা এই সভ্যতার মানুষরা ঠিক কিভাবে হঠাৎ হারিয়ে গেলেন এই পৃথিবীর বুক থেকে, তা আজও রহস্যাবৃত।

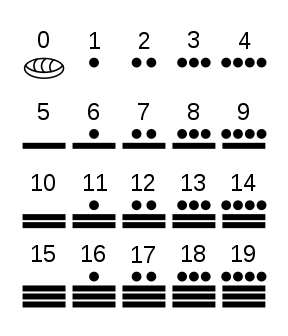
প্রাচীন সভ্যতাগুলোর মধ্যে লিখিত লিপিসমৃদ্ধ এই মায়া সভ্যতাই ছিল একমাত্র সভ্যতা যারা শূন্যকে পরিষ্কারভাবে স্বাধীন সংখ্যার মর্যাদায় বরণ করে নিয়েছিলেন। আপনার পঞ্চাশতম জন্মদিনে কেউ যদি আপনার বয়স জানতে চায়, তাহলে নিশ্চয়ই বলবেন পঞ্চাশ বছর, কিন্তু মায়া সভ্যতার মানুষরা বলতেন, বস্তুত লিখতেন, পঞ্চাশ বছর শূন্য মাস শূন্য দিন। বাঙালীর দীর্ঘসূত্রতার মাপকাঠি ঠিক কি কারণে ‘আঠারো মাসে বছর’ বাক্যবন্ধে প্রতিফলিত হয় তা আমার জানা নেই, কিন্তু মজার ব্যাপার হল এই মায়া সভ্যতার অন্যতম প্রধান সময়পঞ্জিকা ‘হাব’-এ কিন্তু বছর ধরা হত আঠারো মাসে! প্রত্যেক মাসে কুড়ি দিন – শূন্যতম দিন থেকে উনিশতম দিন। আর এভাবে মোট তিনশো ষাট দিন হবার পর পাঁচ দিনের এক বিশেষ ভৌতিক মাস- ‘উয়ায়েব’। এভাবেই বছরের তিনশো পঁয়ষট্টি দিনের হিসেব মেলাতেন মায়া-রা।

এরা সংখ্যাপাতন করতেন ওপর থেকে নীচে, স্থানিয়মান পদ্ধতিতে, কিন্তু কুড়ির এককে, যাকে পরিভাষায় বলে ‘ভাইজেসিমাল’। ওদের মতে বিশ্বব্রম্ভান্ডের সৃষ্টির একটা নির্দিষ্ট দিন ছিল, যেটা আমাদের আধুনিক ক্যালেন্ডারের নিরিখে দাঁড়ায় ১৩ই অগাস্ট, ৩১১৪ খ্রিস্টপূর্বাব্দ। সেই দিনকে যথারীতি শূন্যতম দিন ধরে, যেকোনো গুরুত্বপূর্ণ রাজনৈতিক বা সামাজিক ঘটনার দিন নির্ধারণ করতেন মায়া-রা। আর দক্ষ কারিগরেরা পাথরের স্তেলায় খোদাই করে রাখতেন সেই দিনটার কথা, সময়ের বিভিন্ন এককে ভাগ করে নিয়ে।

যেমন ধরুন, এক হাজার দিনকে আমাদের মতন করে বললে দাঁড়ায় দু’বছর আট মাস সাতাশ দিন। মায়া-দের সময় এককে কুড়ি ‘কিন’ (দিন) ছিল এক ‘উইনাল’ (মাস), আঠারো ‘উইনাল’ ছিল এক ‘টুন’ (বছর), কুড়ি ‘টুন’ ছিল এক ‘কাটুন’, কুড়ি ‘কাটুন’ ছিল এক ‘বাকটুন’, এরকম আরও অনেক অনেক দূর পর্যন্ত। মায়াদের দিন গোনার এই পদ্ধতিকে বলা হয় ‘লং কাউনট’ ক্যালেন্ডার। সবই কুড়ির গুণিতকে, শুধু তৃতীয় ঘরে (অর্থাৎ উইনাল থেকে টুন) আঠারো গুণিত কুড়ি, যা ঘেঁটে ফেলেছিল গাণিতিক স্থানিয়মান পদ্ধতির এক অতিবিশিষ্ট এবং জরুরী প্রয়োজনকে – ভেঙে গিয়েছিল স্থানিয়মানের ছন্দ। আর তাই শূন্যের গানিতিক ধর্মও গিয়েছিল গুলিয়ে। অর্থাৎ স্থানীয় মান পদ্ধতির সঙ্গে সাযুজ্যপূর্ণ গাণিতিক সংখ্যা হিসেবে শূন্যের অবশ্য পালনীয় ধর্মের বিচ্যুতি ঘটে গিয়েছিল মায়াদের ‘শূন্যের’ বেলায়। ফল হিসেবে মায়াদের শূন্যকেও আমাদের আধুনিক শূন্যের জনক বলার রাস্তা বন্ধ হয়ে গেলো।

প্রাচীন ভারতীয় সভ্যতা ও দর্শনে শূন্যের ধারণা

সুপ্রাচীন সভ্যতাগুলির মধ্যে এক অনন্য দার্শনিক উচ্চতায় উঠেছিল আমাদের ভারতীয় সভ্যতা। এর জ্ঞান-বিজ্ঞান-জ্যোতির্বিদ্যা চর্চার ইতিহাসও অতি সমৃদ্ধ। কিন্তু দুর্ভাগ্যের বিষয় প্রাচীন ভারতে সম্রাট অশোকের সময়ের আগে কোন লিখিত লিপি ছিলনা। সবটাই ছিল মুখে মুখে, অর্থাৎ শ্রুতি। বৈদিক যুগে এই ঘরানা জন্ম দিয়েছিল সংক্ষিপ্তকরণ প্রক্রিয়ার, আর সেই সঙ্গে ছন্দবদ্ধ শ্লোক নির্মাণের। এই সূত্রগুলো এতই দুরূহ এবং এতই সংক্ষিপ্ত যে পরবর্তী পর্যায়ের ভাষ্যকারদের টীকার সাহায্য না নিলে প্রায়শই এদের অর্থ বোধগম্য হবার কোন সম্ভাবনাই নেই। সূত্র নির্মাণের অন্যতম প্রধান শর্তই ছিল ‘অল্পাক্ষরং’, অর্থাৎ যতটা সম্ভব অল্প কথায় প্রকাশিত হতে হবে। বলা হয়, কোন সূত্রের অর্থ অবিকৃত রেখে সূত্রকার যদি এক মাত্রাও তাকে সংক্ষিপ্ত করতে পারতেন, তাহলে তিনি নাকি পুত্রলাভের আনন্দ পেতেন!

বেদের যুগ থেকেই ঋষিদের গভীর জ্ঞান-সঞ্জাত দার্শনিক উচ্চারণে আমরা শূন্যের কথা দেখতে পাই। এই শূন্য অবশ্যই গণিতের শূন্যসংখ্যা নয়, কিন্তু শূন্যতার বোধকে এই সভ্যতা দার্শনিক দৃষ্টিকোণ থেকে অত্যন্ত সহজে এবং কৌতুহলের সাথে গ্রহণ করেছিল সন্দেহ নেই। গ্রিক সভ্যতার মতন দার্শনিক মতবাদ এখানে গাণিতিক শূন্যকে রুখে দেবার চেষ্টা করেনি, উলটে বারবার খতিয়ে দেখেছে, অনুভব করতে চেয়েছে শূন্যতার বাঙময় নীরবতাকে। ঋকবেদের নাসদীয় সুক্তই হোক, অথবা বৌদ্ধ মহাযানের মাধ্যমক শৈলীর শূন্যবাদী দর্শনে, কিম্বা তন্ত্রের নিরাকার নিষ্কল শিবের ধারণায়, অথবা নৈয়ায়িকের ‘অভাব’ বোধে – সর্বত্রই দেখতে পাওয়া যায় শূন্যতার জয়গান তথা দার্শনিক বিশ্লেষণ, তাকে বোঝার চেষ্টা, আত্মস্থ করার উন্মুখ আগ্রহ।

প্রাচীন ভারতে গাণিতিক শূন্যের ধারণা ও তার সময়কাল ঘিরে বিতর্ক

এই সামাজিক বাতাবরণে গণিত ও গণিতজ্ঞেরা ছিলেন বৈকি। বেদাঙ্গ জ্যোতিষে গণিতকে তুলনা করা হয়েছে নাগের মাথার মণির সাথে, অথবা ময়ূরের মাথার শিখার সাথে। স্পষ্ট উচ্চারণে বৈদিক ঋষি ঘোষণা করেছেন সমগ্র বেদাঙ্গ শাস্ত্রের মধ্যে গণিত শাস্ত্রের শ্রেষ্ঠত্ত্বের কথা। কাজেই এই সামাজিক বাতাবরণে যেদিন গণিতজ্ঞেরা বুঝতে পেরেছিলেন সংখ্যা হিসেবে শূন্যের প্রয়োজন ও গুরুত্ত্বকে, সমাজের অন্য দিকপালেরা তাতে বাধার সৃষ্টি করেননি।

কিন্তু সময়টা ঠিক কবে নাগাদ ছিল? দুর্ভাগ্যের বিষয় খ্যাতনামা পণ্ডিতেরা এ নিয়ে একমত নন। আজকের আধুনিক গণিতের শূন্যের পূর্বপুরুষ যে ভারতীয় দশমিক সংখ্যাতন্ত্রের শূন্য, এ বিষয়ে মোটের ওপর অনেক বিশেষজ্ঞই একমত হলেও, সময়ের ব্যাপারে তাদের পছন্দ প্রায় হাজার খানেক বছর এদিক-ওদিক ছড়িয়ে যায়। কেউ কেউ গুপ্ত যুগের আগে ভারতীয় শূন্যকে খুঁজে পান না, হয়ত বা পেতে চান না – লিখিত তথ্যের অভাব তাদের যুক্তির মূল হাতিয়ার। তাঁদের ধ্যান- ধারণায় আধুনিক জ্ঞান-বিজ্ঞানের যা কিছু ভাল তার সবই নাকি এসেছে প্রাচীন গ্রীক সভ্যতা থেকে এবং তা আলেকজান্ডারের সাম্রাজ্য বিস্তারের পথ বেয়েই নাকি ছড়িয়ে পড়েছিল বৃহত্তর পৃথিবীতে। শূন্যকে তাঁরা খোঁজেন গ্রীক অক্ষর ‘ওমিক্রন’-এ অথবা রোমান সাম্রাজ্যের প্রায় মূল্যহীন মুদ্রা ‘ওবল’- এর অদ্যাক্ষরে।

পাল্টা মতও খুব জোরালো। ‘ওমিক্রন’ বা ‘ওবল’- এর যুক্তিকে নস্যাৎ করে তাঁরা শূন্যের উপস্থিতি দেখিয়েছেন ভারতীয় ছন্দসূত্রাকার আচার্য পিঙ্গল-এর ছন্দসূত্রে, এমনকি পাণিনির ব্যাকরণেও। এগুলো অবশ্যই অংকের বই নয়, কিন্তু যে স্বাচ্ছন্দ্যের সাথে বৈয়াকরণ পাণিনি তাঁর ব্যাকরণে শব্দের ব্যুৎপত্তির বিশ্লেষণ করতে গিয়ে শব্দাংশের অবলুপ্তিকে সুত্রায়িত করেছেন (পরিভাষায় বলে, “অদর্শনম লোপহ”), তার সাথে গাণিতিক শূন্যের “প্লেসহোলডার” বা ফাঁক-বোঝাই করার ভুমিকার অসামান্য ধাঁচ-ভিত্তিক মিল, এঁদের উদ্বুদ্ধ করেছে সমকালীন সমাজে গাণিতিক শূন্যের ধারণার অস্তিত্ব নিয়ে গবেষণা করতে। দেশী-বিদেশী এইসব বিশেষজ্ঞদের অনেকের মতে, সেই সময়ে গণিতের শূন্য সংখ্যার ধারণা জানা ছিল বলেই না পাণিনির মতন একজন অগণিতজ্ঞ বৈয়াকরণও তা এত সহজে তার নিজস্ব বিষয়ের বিশ্লেষণে সমান্তরালভাবে প্রয়োগ করতে পেরেছেন। আর একটু রক্ষণশীল ঘরানার অনেকের দাবী হোল, মহাপণ্ডিত পাণিনির দেখানো পথেই একদিন গণিতজ্ঞেরা বুঝতে পেরেছিলেন গণিতে সংখ্যা হিসেবে শূন্যের প্রয়োজন কি। তাই এর অস্তিত্বকে কম বেশি খ্রিস্টপূর্ব পাঁচশতে ঠেলে দেওয়া যেতেই পারে।

লিখিত প্রমাণের অভাবে সময়কাল নিয়ে ধোঁয়াশা

পিঙ্গল ছন্দসূত্রের উদাহরণ আরও অনেক জোরালো এবং সরাসরি। অষ্টম অধ্যায়ের “রূপে শূন্যম” এবং “দ্বি-শূন্যে” সূত্র দুটিতে যে “শূন্য” শব্দকে দেখা যাচ্ছে তা গাণিতিক শূন্যই বটে এবং এর আগে পরে আরও দুটি সূত্র মিলিয়ে টীকাকার হলায়ুধের ব্যাখ্যা অনুযায়ী মহামুনি পিঙ্গল যে গণনা করেছেন তা আজকের পরিভাষায় গণিতের “সমবায় (Combination)” গণনা ছাড়া কিছু নয়। বৈদিক ছন্দের মাত্রার বিশ্লেষণে লঘু এবং গুরু স্বরের সাপেক্ষে কোনো প্রদত্ত মাত্রার সমবৃত্ত ছন্দবিন্যাস প্রত্যেক পাদে কত রকম হতে পারে, তাই-ই ছিল পিঙ্গল মুনির আলোচ্য। আর এইসব বিশ্লেষণ করতে গিয়ে তিনি যা যা দেখিয়েছেন, তার অনেক কিছুর পুনরাবিষ্কার হয়েছে প্রায় দু হাজার বছর পরে আধুনিক নবজাগরণ-উত্তর ইউরোপে। আমরা তার কাউকে চিনি “পাস্কাল-ত্রিভুজ” বলে, কাউকে বলি দ্বি-নিধানি (binary) সংখ্যাতন্ত্র, যার শ্রেয় আজ বর্তায় যথাক্রমে পাস্কাল ও লাইবনিৎস এর নামে।

পণ্ডিতেরা বলেন পিঙ্গলের সময়কাল মোটামুটিভাবে খ্রিষ্টপূর্ব দ্বিতীয় বা তৃতীয় শতকে, যদিও এ নিয়েও যথারীতি মতবিরোধ রয়েছে। এমনকি এমন মতও আছে যে গোটা অষ্টম অধ্যায়টাই নাকি বহুকাল পরে অন্য কারো লেখা! এই মতের খণ্ডনও রয়েছে বইকি! আসলে প্রাচীন ভারতের ইতিহাস ঘাঁটতে গেলেই যে দুর্ভাগ্যজনক শূন্যতার সামনে পড়তে হয় তা হলো লিখিত প্রত্যক্ষ প্রমাণের অভাব – আর তাই এতরকম মতামত, যুক্তি, প্রতিযুক্তি।

লিখিত লিপি সমৃদ্ধ সময়ে সরাসরি শূন্যকে খুঁজতে গেলে, সেটা গিয়ে দাঁড়ায় আর্যভট-এর বা পরবর্তী পর্যায়ের ব্রহ্মগুপ্ত-এর সময়ে, অর্থাৎ কিনা খ্রিষ্টীয় ষষ্ঠ শতক থেকে শুরু করে অষ্টম শতকে। একথা ঠিক যে আর্যভট সংখ্যা পাতনের দশমিক সূত্র উল্লেখ করেছেন, বা ব্রহ্মগুপ্তই প্রথম পরিষ্কার বলেছেন কোনো সংখ্যা থেকে সেই সংখ্যাকে বিয়োগ করলে বিয়োগফল শূন্য হয়, সঙ্গে ঘোষণা করেছেন শূন্যের নানান গাণিতিক ধর্ম। এর পরবর্তী পাঁচ-ছ’শ বছরে আরো অনেক গণিতজ্ঞই তাদের রচনার শূন্যগণিত অংশে লিখেছেন শূন্য দিয়ে পাটিগাণিতিক গণনার নানান ধর্ম। হ্যাঁ, এর মধ্যে শূন্য দিয়ে ভাগ করার কথাও রয়েছে একাধিক জায়গায়, যা আজকের গণিতে সাধারনভাবে অসংজ্ঞায়িত ধরা হয়। তবে ভাস্করাচার্য্য-এর বলা “খহর” এর ধারণা, অর্থাৎ তাঁর ভাষায় “খ ভাজিত রাশি” কি অসামান্য নতুন গণিত-এর সন্ধান দিতে পারে তা ইদানিং কালে গণিত-ভারতী পত্রিকায় প্রকাশিত এক রচনায় দেখিয়েছেন কেনটাকি বিশ্ববিদ্যালয় এর গণিতের অধ্যাপক আবিনাশ শাঠ্যে।

তবে এসব অন্য গল্প। সে যাই হোক, ভারতীয় সভ্যতার প্রাচীনতা এবং তার সুগভীর জ্ঞানভাণ্ডারে থাকা শত শত প্রত্যক্ষ ও পরোক্ষ উদাহরণ একথার পক্ষেই বলে যে এখানে শূন্য সহ দশমিক সংখ্যাতন্ত্রের ধারণার শুরু কিছুতেই এত পরে হতে পারে না। এর উন্মেষ ঘটেছিল বহুকাল আগে – তা সে লিখিত ইতিহাস থাকুক বা না থাকুক। মাত্র কিছুকাল আগে এক ফরাসী বিশেষজ্ঞ জর্জেস ইফ্রা তাঁর বইতে বিশদে বলেছেন এক জৈন বিশ্ববীক্ষা গ্রন্থের কথা, যার নাম “লোকবিভাগ”। এর রচনাকাল নির্ধারণ করা যাচ্ছে বইতে দেওয়া তথ্যের জ্যোতির্বিদ্যা ভিত্তিক সূত্র বিশ্লেষণ করে। তখনকার গ্রহ নক্ষত্র অবস্থানের নিখুঁত গাণিতিক সময় গণনা থেকে দেখা যাচ্ছে এই বই রচিত হয়েছিল চারশো আটান্ন খ্রিষ্টাব্দে এবং এই বইতে পরিষ্কার ভাষায় উল্লেখ রয়েছে শূন্য সহ স্থানীয় মান পদ্ধতির সংখ্যা পাতনের। শুধু তাই নয়, পরিশেষে “লোকবিভাগ” এর লেখক বলেছেন – এই সব তত্ত্ব আমরা বহুকাল আগে থেকেই জানি, সেই মুনি সর্বনন্দিন এর সময় থেকেই। আর এই বিশেষ মুনিবরের সময়কাল? সেটা আবারও আমাদের অজানা।

ভারত থেকে বহির্বিশ্বে শূন্যের চলন

ভারতীয় গণিতের এই রত্নখনির সন্ধান পেয়েছিল আরবেরা। পারস্যদেশের খলিফাদের রাজসভার সভাপণ্ডিত গণিতজ্ঞদের হাতে অনুদিত হয়ে টিকে গিয়েছিল এই প্রাচীন সভ্যতার গণিত-জ্ঞানভাণ্ডার। পরবর্তী সময়ে নবজাগরণের সূচনায় ল্যাটিনে অনুবাদ হয়ে এই শূন্যসহ দশমিক সংখ্যাতন্ত্র ক্রমশ প্রবেশ করেছিল ইউরোপে। সে যাত্রাপথ খুব মসৃণ ছিল, এমনটা নয়। এই কারনেই ইউরোপে এই সেদিন পর্যন্ত এইসব সংখ্যাচিহ্নদের বলত আরবিক সংখ্যাচিহ্ন। এখন অবশ্য সেই ভুল আর কেউ করেনা। ভারতের অবদান স্বীকার করে এর নতুন নাম হয়েছে হিন্দু-আরবিয় সংখ্যাচিহ্ন।

প্রাচীন ভারতে গাণিতিক শূন্যের সবচেয়ে চালু নাম ছিল ‘খ’, অর্থাৎ আকাশ অথবা গগন, অন্তরীক্ষ বা জলধরপথ, ইত্যাদি কত বিচিত্র প্রতিশব্দ – পরিভাষায় যাদের বলে ‘ভূতসংখ্যা’ (word numerals)। কেমন ছিল ভারতীয় শূন্যের আদি চেহারা? বরাহমিহিরের ‘সূর্যসিদ্ধান্তে’ বা সুবন্ধুর নাটক ‘বাসবদত্তায়’ রয়েছে শূন্যকে বিন্দুর সঙ্গে তুলনা (শূন্যবিন্দবহ্), অমরকোষের কোষকার অমরসিংহ বলেছেন, শূন্য হলো ফাঁকা, তুচ্ছ বা রিক্তক। কেউ এর নাম দিয়েছেন ‘ছিদ্র’। অন্যত্র পাওয়া যায় ‘রন্ধ্র’। নাম-মাহাত্ম্য থেকে এর আকৃতির গোল ছাঁচ সহজেই অনুমেয়। তবে শুরুতে সম্ভবত গোলের ভেতরটা ফাঁকা থাকত না, ভরাট করে দেওয়া হত। পরে কোন এক সময় থেকে, হয়ত বা সময় বাঁচাতেই সেই প্রথা উঠে যায়।

শূন্যের লিখিত প্রমাণ – যা পাওয়া যায়

এই ভরাট শূন্যকে লিখিত আকারে দেখা যায় বার্চ গাছের ছালে লেখা বকশালি পান্ডুলিপিতে, বর্তমানে অক্সফোর্ডের এক বিশেষ পাঠাগারে যা সংরক্ষিত রয়েছে। এর রচনার সময়কাল নিয়েও যথারীতি নানা মুনির নানা মত। কেউ একে দ্বিতীয় শতকে লেখা বলেন, তো কেউ বলেন একেবারে দ্বাদশ শতকে, অন্য অনেকে আবার এর মাঝামাঝি কোথাও। এদিকে গত বছর সেপ্টেম্বর মাসে ঘোষিত এক রেডিও-কার্বন পরীক্ষার ফলাফল অনুযায়ী এটা নাকি কোন এক বিশেষ সময়ের রচনা নয়। সব মিলিয়ে এই বিতর্ক এখন জমজমাট।

পাথরে খোদাই করা প্রাচীনতম শূন্য সংখ্যা দেখতে হলে যেতে হবে মধ্যপ্রদেশের গোয়ালিয়র দুর্গে। সেখানকার চতুর্ভুজ বিষ্ণু মন্দিরের উৎকীর্ণ শিলালিপিতে দেখা যায় নবম শতাব্দীর কোন এক রাজা ভোজদেব ওই মন্দির সংলগ্ন একখণ্ড জমি দেবত্র করেছেন। যেখানে ফুলের চাষ হবে, সেই ফুল উৎসর্গ হবে ভগবান বিষ্ণুর পূজায়। জমির মাপ বোঝাতে গুপ্ত যুগের নাগরি লিপিতে লেখা ২৭০ হস্ত দৈর্ঘ্য ও ৫০ হস্ত প্রস্থের কথা, যা আন্তর্জাতিকভাবে স্বীকৃত আমাদের জানা আধুনিক শূন্যের বর্তমান চেহারার সবচেয়ে প্রাচীন লিখিত লিপির নিদর্শন। বর্তমান চেহারার লিখিত শূন্য আরও অনেক আছে, তবে তা তাম্রপত্রে খোদাই করা এবং এদের সময়কাল অপেক্ষাকৃত বেশী পুরানো হলেও এগুলোর সময়কালের দাবীর সত্যতা নিয়ে পণ্ডিতেরা একমত নন।

শূন্য থেকে জিরো

বস্তুত শুধুমাত্র ভারতীয় প্রসঙ্গে শূন্যকে সব দিক থেকে দেখাতে হলে যা লিখতে হবে, তা একটা গোটা বইয়ের উপজীব্য হতে পারে। সংস্কৃত শব্দ ‘শূন্য’ এসেছে শুনা (+যৎ প্রত্যয়) থেকে, যা মূল ধাতু ‘শ্বি’- এর পুরাঘটিত অতীত রূপ। মূল ধাতুর প্রত্যক্ষ অর্থ ছিল ‘ফুলে ওঠা ফাঁপা গহ্বর’, যে অর্থে ‘শুনম্’ শব্দ ব্যবহৃত হয়েছে ঋগ্বেদে, নিহত পশুদের পচনশীল ফুলে ওঠা দেহাবশেষের বর্ণনায়। সময়ের সাথে এর অর্থ বিস্তারিত হয়েছে ‘অভাব’ বোঝাতে – এমন কিছু, যা থাকার কথা ছিল কিন্তু বাস্তবে নেই! ভাষা বিজ্ঞানীরা বলেন ‘সেমান্টিক এক্সটেন্সন’। এই না থাকা, অর্থাৎ ‘নেই’, যতটা নঞর্থক, ততটাই অস্ত্যর্থক – আপাত অভাব যেন অসীম সম্ভাবনার উদ্ভাসের প্রতিক্ষায় উন্মুখ তাকে বরণ করে নিতে – যেমনটা হয় মাতৃগর্ভের শূন্যতা।

আরবদের অনুবাদ ‘শূন্য’ শব্দের এই দার্শনিক দ্যোতনাকে ধরতে পারেনি – ভারতীয় দর্শনের আত্মার সন্ধান ছাড়া তা ধরা সম্ভবও ছিলনা। তাই আরবিয় আক্ষরিক অনুবাদে ‘শূন্য’ হয়েছিল ‘সিফ্র’ (sfr), যা শুধুই অভাব বোধের নঞর্থক প্রতিধ্বনি। পরবর্তী সময়ে ল্যাটিন অনুবাদকদের হাতে পড়ে বদলাতে বদলাতে এর নাম দাঁড়ায় সিফ্রা, সিফ্রে, জিফ্রা, জাইফ্রা ইত্যাদি নানান রকম। ইতালির পিসা অঞ্চলের ব্যবসায়ী বোনাচ্চিওর গণিতজ্ঞ ছেলে লিওনার্দো, যিনি গণিত জগতে ফিবনাচ্চি নামেই বেশী পরিচিত, তিনি ছোটবেলায় আফ্রিকার আরব উপনিবেশে ঘুরে বেড়িয়েছেন ব্যবসায়ী বাবার সঙ্গে। সেখানেই আরবদের কাছে তাঁর এই সংখ্যা পদ্ধতিতে হাতেখড়ি, সঙ্গে শেখা মাত্র দশটা সংখ্যাচিহ্ন ব্যবহার করে যত বড় খুশি সংখ্যা লিখতে পারার দশমিক পদ্ধতি। বড় হয়ে ত্রয়োদশ শতকে তিনি যখন রচনা করলেন ‘লিবের আবাচি’ অর্থাৎ সংখ্যাদের বই, সেখানে তিনি বললেন আরবদের এই অসামান্য সংখ্যাতন্ত্রের কথা – তাঁর লেখনীতে জিফ্রা দাঁড়ালো ‘জেফিরাম’, ল্যাটিনে যার মানে ‘পশ্চিমের মলয় বাতাস’, খুবই হালকা, তুচ্ছ – প্রায় অনুভুতই হয় না এত মৃদু। এই জেফিরাম থেকে ভেনিসিয় কথ্য ভাষায় একদিন তৈরি হোল নতুন প্রতিশব্দ ‘জেফিরো’ – ক্রমশ ‘জেরো’, যার ইংরেজি তুতভাই হোল ‘জিরো’ – আমাদের আধুনিক শূন্য।

উপসংহার

গণিত ইতিহাসের এই অংশের পুনরুদ্ধারের বিষয়টা অনেকটা যেন বাচ্চাদের সেই ধাঁধার খেলার মতন, যেখানে অনেকগুলো টুকরো জুড়ে তৈরি করতে হয় প্রকৃত চিত্রকে – তফাতের মধ্যে এক্ষেত্রে বেশ কিছু টুকরোই গেছে হারিয়ে, হয়ত বরাবরের মতন। তাই যুক্তির সঙ্গে কল্পনার মিশেল দিয়ে পণ্ডিতেরা তৈরি করেন নতুন নতুন চিত্রকল্প। কখনও আবিষ্কৃত হয় নতুন একটা টুকরো, যা আগে সকলের কাছেই ছিল অজানা। অমনি বদলে যায় চিত্রকল্প, বিকশিত হয় নতুন সম্ভাবনা। এ খেলার কোন শেষ নেই।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/zero-02

print