শূন্য (প্রথম পর্ব)

পার্থসারথি মুখোপাধ্যায়

(Narendrapur Ramkrishna Mission College)

 

11 May 2018

Link: https://bigyan.org.in/zero-01

মনে করুন আপনার কাছে দুটো কলম আছে। আপনি তার থেকে একটা কাউকে দিয়ে দিলেন। এবার যদি প্রশ্ন হয় আপনার কাছে ক’টা কলম আছে, আপনি নিশ্চয়ই উত্তরে বলবেন – একটা আছে। ধরুন এরপর সেই কলমটাও আপনি দিয়ে দিলেন। এবার যদি একই প্রশ্ন আপনাকে আবার করি ? অবশ্যই আপনি বলবেন – একটাও নেই। একটু খুঁটিয়ে উত্তরের ভাষাদুটোকে লক্ষ্য করুন। প্রথমবার ‘আছে’ দিয়ে করা প্রশ্নের উত্তর ‘আছে’ দিয়ে দিলেও দ্বিতীয়বারে কিন্তু উত্তর হয়েছে ‘নেই’ দিয়ে। এই দ্বিতীয় উত্তরটাকেও যদি ‘আছে’ দিয়ে বলতে হয়, তাহলে যে সংখ্যার ধারণা কাজে লাগে তা হলো শূন্য। অর্থাৎ ‘একটাও নেই’ কথাটা পুরোপুরি ভাষায় বলা। সংখ্যার ধারণা ব্যবহার করে হ্যাঁ-বোধক বাক্যে উত্তরটা দিতে হলে বলতে হবে ‘শূন্যটা আছে’ – যা আমরা বাস্তবে বা ব্যবহারিক জীবনে কখনোই বলি না, বস্তুতঃ বলার দরকার পড়ে না। আর এই দরকার না পড়ার ব্যাপারটা মিলিয়ে নেওয়া যায় প্রাগৈতিহাসিক যুগ থেকে সময়ের স্রোতে গা ভাসালে।

আজ থেকে হাজার পঁচিশ বছর আগেকার কথা। পৃথিবীর নানান কোণে ছড়িয়ে-ছিটিয়ে থাকা প্রাচীন মানুষেরা তখনও তথাকথিত সভ্যতার আলোয় আলোকিত হননি। সেই সময় থেকেই মানুষ গুণতে শিখেছে প্রয়োজনের তাগিদে, হয়তো বা পালিত পশুর হিসেব রাখতে গিয়ে। সময়ের বিবর্তনে একদিন এই বস্তুগণনার ধারণা থেকেই জন্ম হয়েছে সংখ্যার ধারণার – দেশ কালের বিচারে নানান প্রাচীন সভ্যতায়, নানান রূপে, নানান নামে, নানান গাণিতিক পরিকাঠামোয়। এই সুপ্রাচীন সভ্যতাগুলোর ভৌগোলিক অবস্থান ও ইতিহাস ঘেঁটে দেখা যায় যে এদের অনেকেই অন্যদের সম্বন্ধে কিছুই জানতেন না, জানা সম্ভবই ছিলো না। তবুও কি আশ্চর্য কথা, এরা প্রত্যেকেই নিজেদের মতন করে সৃষ্টি করেছিলেন একান্ত নিজস্ব সংখ্যাতন্ত্র এবং তার প্রয়োগ করেছিলেন তাঁদের একান্ত নিজস্ব ব্যবহারিক ও সামাজিক সমস্যার সমাধানে। আর এই প্রয়োগের সার্থকতায় উজ্জ্বল হয়ে উঠেছিলো এই সব অসামান্য সভ্যতা, সৃষ্টির নানান আঙ্গিকে – কেউ স্থাপত্যে, কেউ জ্ঞানচর্চায়, কেউ বা গ্রহ-নক্ষত্রের অবস্থান পূর্বানুমানে।

শূন্যের প্রয়োজন

প্রাথমিকভাবে তখনকার দিনে ‘সংখ্যা’ বলতে আজকের পরিভাষায় বললে মূলতঃ ধনাত্মক পূর্ণসংখ্যাদেরই বোঝাতো। কোন সভ্যতায় কে এদের আবিষ্কর্তা তা কেউ জানে না। এক আধুনিক গণিতজ্ঞের কথায়, “God created Natural numbers, everything else is man’s handiwork” (ভগবান প্রাকৃতিক সংখ্যা সৃষ্টি করেছিলেন, বাকিসব মানুষের কীর্তি)।

আর এই মানুষের কীর্তির মধ্যেই পড়ে শূন্য। মানুষকে এর আবিষ্কার করতে হয়েছে আলাদা করে, সভ্যতার অনেক বিকশিত পর্যায়ে এসে – বাধ্য হয়ে, প্রয়োজনের তাগিদে। কি ছিলো সেই প্রয়োজন ? ‘শূন্য’-কে সংখ্যা হিসেবে ব্যবহার করতে শেখার আগে কিভাবেই বা সেই প্রয়োজন সামাল দিতেন প্রাচীন মানুষেরা? নাকি বেসামাল হয়ে পড়তো তাদের গণনাকার্য? এর উত্তর জানতে গেলে মানব-সভ্যতার অন্ততঃ পাঁচ হাজার বছরব্যাপী সময়ের ইতিহাস ঘাঁটতে হবে। সে ইতিহাস যেমন রোমাঞ্চকর, তেমনই কৌতূহল জাগানো। বর্তমান আলোচনার সংক্ষিপ্ত পরিসরে সে বিস্তৃতির অবকাশ নেই। বড়োজোর কিছু কিছু পরিপ্রেক্ষিতকে ওপর ওপর ছুঁয়ে দেখা যেতে পারে মাত্র।

শূন্যের ধারণা প্রথমেই আসেনি

সভ্যতার বিবর্তনের এই বিশেষ প্রেক্ষাপটকে সময়ের মাপকাঠিতে ফেলে, তার সমান্তরালে যদি লক্ষ্য করেন আজকের যুগের একজন মানবশিশুর সংখ্যার ধারণা বা বোধকে আত্মস্থ করার প্রক্রিয়া, তাহলে এক অদ্ভুত মিল খুঁজে পাবেন।

ছোটবেলার রঙচঙে বইগুলোতে সংখ্যার প্রাথমিক ধারণা দেওয়া হয় ধরা-ছোঁয়ার মধ্যে থাকা বস্তুদের গুনতে শেখার সূত্রে। মনে পড়ে, দুটো রঙীন ঘুড়ির পাশে লেখা ‘২’ বা তিনটে আপেলের পাশে লেখা ‘৩’-কে? খেয়াল করে দেখুন, এই পর্যায়ের আলোচনায় কখনোই শূন্যের কথা আসে না। আসবে কি করে ? ধরা-ছোঁয়ার বস্তুজগতের উদাহরণে শূন্যকে ধরা যায় না যে। শুধুমাত্র মানসিক বিকাশের আরোও অনেকটা উঁচু ধাপে এসে তবেই বোঝা সম্ভব গাণিতিক সংখ্যা হিসেবে শূন্যের প্রয়োজনকে – যেমনটা এই লেখার শুরুতে আমরা আলোচনা করেছি। মানবসভ্যতার বিকাশের নিরিখেও ঘটনাটা অনেকটা এমনধারাই ঘটেছিলো – শুধু সময়ের মাপকাঠিটাই ছিলো যা আলাদা। আজকের শিশু যেটা বুঝে নেয় কয়েক বছরের পরিণত বুদ্ধিতে, অতীত ইতিহাস বলে, মানবসভ্যতার জন্য সেই সময়টা লেগেছিলো কয়েক হাজার বছরের।

শূন্য ছাড়া বড় সংখ্যা লিখতে গেলে

সংখ্যার ধারণা তৈরী হবার পর, ধাপে ধাপে উঠে এসেছিলো ক্রমশঃ বড় বড় সংখ্যাদের চিন্তা, তাদের নতুন নতুন নাম, আর তাদের তৈরী করার নানান প্রকরণ। কোথাও লিখিত আকারে, কোথাও বা শুধুই মুখে মুখে। এর ফলে তৈরী হয়েছিলো নানান সংখ্যাপাতন পদ্ধতি। কখনো সেটা হয়েছিলো স্থানীয় মান অনুসারে, কখনো বা পাশাপাশি বসানো নানান সংখ্যাচিহ্নর মধ্যে যোগ (বা বিয়োগ)-কে ভিত্তি করে নতুন নতুন সংখ্যার ধারণা তৈরী হয়েছিলো।

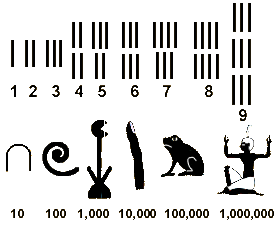
যেমন মিশরের চিত্রলিপি ঘেঁটে পন্ডিতরা দেখেছেন তাদের সংখ্যাপাতন পদ্ধতি ছিলো যোগ-ভিত্তিক। অর্থাৎ পাশাপাশি যে সংখ্যাচিহ্ন দেখা যাচ্ছে তাদের মানের মোট যোগফলই হলো বলতে চাওয়া সংখ্যা। ব্যাপারটা অনেকটা রোমান সংখ্যাপাতনের মতন (যদিও রোমান সংখ্যাপাতনে বিয়োগের ভূমিকাও রয়েছে)। অর্থাৎ, উদাহরণ হিসেবে আজকের সংখ্যাতন্ত্রের সংখ্যা-চিহ্নদের ধার করে যদি ১১ লিখি, মিশরীয় মতে তা এগারো বোঝাবে না, বোঝাবে ১+১ = ২ (দুই)। যেমন রোমান মতে ৫১ (VI) বলতে বোঝায় ৬ (ছয়, অর্থাৎ ৫+১) আবার ১৫ (IV) বলতে বোঝায় ৪ (চার, অর্থাৎ ৫-১), ইত্যাদি। অর্থাৎ এই ধরণের সংখ্যাতন্ত্রে সংখ্যার স্থানীয়মানের (যেমন, আধুনিক দশমিক সংখ্যাতন্ত্রের এককের ঘর, দশকের ঘর, শতকের ঘর ইত্যাদির) কোনো ভূমিকা ছিলো না। ফলে যত নতুন সংখ্যার কথা ভাবতে হতো ততই নতুন নতুন সংখ্যা-চিহ্নের দরকার পড়তো, আর সংখ্যাদের মধ্যে সাধারণ পাটিগণিতও হয়ে উঠতো ক্রমশঃ জটিল থেকে জটিলতর।

এই সব সংখ্যাতন্ত্রে শূন্যের কোনো জায়গা ছিলো না। ভাবতে পারেন, অমন যে অসামান্য গ্রীক সভ্যতা, যাদের পথে শেখা জ্যামিতির প্রমাণশৈলী আজও পৃথিবীর সর্বত্র গাণিতিক যুক্তিগ্রাহ্যতার প্রাথমিক পাঠ হিসেবে সমাদৃত হয়, তাদের সংখ্যাতন্ত্রে সবচেয়ে বড়ো সংখ্যা ছিলো মোটে দশ হাজার (মিরিয়াড বা মিরিওরাই)। ভাবছেন দশ হাজার লিখতে গেলেই তো শূন্য লাগতো! মোটেই নয়। ওঁরা লিখতেন ‘M’- আর এই চিহ্নের মানেই ছিলো দশ হাজার!

মাঠে নামলেন আর্কিমিডিস

একসময় গণিতজ্ঞ আর্কিমিডিস-এর মাথায় ঢুকলো সমগ্র বিশ্ব বালির দানা দিয়ে ভরে ফেলতে হলে কত দানা বালি লাগবে তা গণনা করে বার করবেন! তখনকার দিনে বিশ্ব-ব্রহ্মাণ্ড বলতে ওরা বুঝতেন খালি চোখে দেখা আকাশের গোলককে। কিন্তু সেই গোলকের আয়তনকে বালির দানা দিয়ে ভরাতে গেলে যে আয়তনভিত্তিক অঙ্ক কষতে হবে, তা ‘দশ হাজার’ সংখ্যায় তো কুলোবে না! দশ হাজার বালির আয়তন কতই বা হবে!

কিন্তু তিনি তো আর্কিমিডিস। তিনি তৈরী করে নিলেন নতুন এক সংখ্যাতন্ত্র। ঘোষণা করলেন যে দশ হাজার থেকে একটা দ্বিতীয় ধাপ শুরু হচ্ছে। প্রথম ধাপে দশ হাজারকে দ্বিতীয় ধাপের “এক” হিসেবে ধরা হচ্ছে। অর্থাৎ, গণনাটা এইরকম:

(ধাপ ১: ১), (ধাপ ১: ২), (ধাপ ১: ৩), …, (ধাপ ১: ১০০০০ = ধাপ ২: ১), (ধাপ ২: ২), (ধাপ ২: ৩), …, (ধাপ ২: ১০০০০),…

আর এখান থেকে গুনতে শুরু করে দ্বিতীয় ধাপে যখন ‘দশ হাজার’ হবে, সেটা হলো তৃতীয় ধাপের ‘এক’। এই সংখ্যাতন্ত্রে দশ হাজারের থেকে বড়ো সংখ্যা বোঝাতে আসলে দুটি সংখ্যার ব্যবহার হচ্ছে: প্রথমটা হলো ‘ধাপ’-সম্পর্কিত সংখ্যাটা, দ্বিতীয়টা সেই ‘ধাপ’-এ কতদূর এগোনো হয়েছে, সেই সংখ্যাটা। কিন্তু দুটো সংখ্যাই নিজেরা দশ হাজারের কম, তাই হাতে মজুত সংখ্যাচিহ্নের সাহায্যেই এদের বোঝানো যায়।

এইভাবে চলবে দশ হাজার ‘দশ হাজার’ অব্দি (অর্থাৎ – মিরিয়াড মিরিয়াড, যা আজকের সংখ্যাচিহ্নে ১০৮ এর সমতুল্য)। দশ হাজারতম ধাপে যখন দশ হাজার আসবে, সেই সংখ্যাটিকে আর এভাবে বোঝানো যাবে না। আর্কিমিডিস করলেন কি, ওই অব্দি পাওয়া সংখ্যাগুলোকে তিনি করলেন প্রথম পর্বভুক্ত। অর্থাৎ, ‘পর্ব’ বলে একটা নতুন স্তরের সৃষ্টি হলো। প্রথম পর্বের দশ হাজারতম ধাপের দশ হাজার সংখ্যাটিকে দ্বিতীয় পর্বের ‘এক’ ধরে তারপর আবার নতুন করে শুরু হলো উচ্চতর পর্ব গণনা। গণনাটা হলো এইরকম:

(পর্ব ১: ধাপ ১: ১), (পর্ব ১: ধাপ ১: ২), …, (পর্ব ১: ধাপ ১: ১০০০০),
(পর্ব ১: ধাপ ২: ১), (পর্ব ১: ধাপ ২: ২), …, (পর্ব ১: ধাপ ২: ১০০০০),
…..
(পর্ব ১: ধাপ ১০০০০: ১), (পর্ব ১: ধাপ ১০০০০: ২), …, (পর্ব ১: ধাপ ১০০০০: ১০০০০)
(পর্ব ২: ধাপ ১: ১), (পর্ব ২: ধাপ ১: ২), …, (পর্ব ২: ধাপ ১০০০০: ১০০০০), ….

অর্থাৎ, এবার একটা সংখ্যাকে বোঝাতে তিনটে সংখ্যার ব্যবহার হলো: পর্ব, ধাপ, ধাপ-এর মধ্যে সংখ্যা। তিনটে সংখ্যা-র কোনোটাই দশ হাজার ছাড়াবে না, তাই হাতে মজুত সংখ্যাচিহ্নে কুলিয়ে যাবে। এইভাবে গণনা চলতে থাকবে।

অসামান্য কল্পনাশক্তি নিঃসন্দেহে, কিন্তু এরই মধ্যে দেখতে পাওয়া যাচ্ছে শূন্যের ধারণার অভাবজনিত বিভ্রান্তি।

আর্কিমিডিস-এর মতো সংখ্যাতন্ত্র আমরাও অজান্তে ব্যবহার করি

ব্যাপারটা বুঝিয়ে বলতে আজকের দশমিক স্থানীয়মান-ভিত্তিক সংখ্যাতন্ত্রে সংখ্যাপাতন সাপেক্ষে একটা উদাহরণ দেওয়া যাক। দশমিক সংখ্যাতন্ত্রে একক, দশক (অর্থাৎ ১০ এর ঘর, যা দ্বিতীয় ঘর), শতক (অর্থাৎ একশো, মানে দশ এর বর্গের ঘর, যা তৃতীয় ঘর) ইত্যাদি হয়ে কোটি (অর্থাৎ ১ এর পর সাতটা শূন্য, মানে অষ্টম ঘর) পর্যন্ত আমরা সবাই স্বচ্ছন্দ। কিন্তু তারপর? আরও বড় সংখ্যার জন্য বরাদ্দ ঘর রয়েছে বইকি। বস্তুত এর কোনো শেষ নেই।

এবার শুধু শূন্য বসিয়ে ক্ষান্ত না হয়ে যদি আলাদা আলাদা নাম চান, তাও আছে ১৯৪ তম (মতান্তরে ২৫০ তম) ঘর পর্যন্ত, শাস্ত্রে যার নাম ‘শীর্ষপ্রহেলিকা’! কিন্তু বাস্তবে আমরা কোটি ছাড়িয়ে গেলে ব্যাপারটাকে ওই আর্কিমিডিসের মতন করেই ঘুরিয়ে নি। তাই তো আজকের যুগে খবরের কাগজ খুললে মাঝে মধ্যেই হাজার কোটি ছাড়িয়ে কয়েক ‘লক্ষ কোটি’ টাকার কেলেঙ্কারির কথাও চোখে পড়ে! সংখ্যাটা ‘কোটি কোটি’ হওয়া শুধু সময়ের অপেক্ষা।

তবে আর্কিমিডিসের সময়ের সাথে এর একটা মৌলিক তফাৎ আছে। আমরা এক কোটিকেই ‘এক’ ধরে পরের ধাপ শুরু করি না, শুরু করি এক কোটি এক থেকে। ‘এক কোটি’ আমাদের কাছে পরের ধাপের ‘শূন্য’, যা আর্কিমিডিস জানতেন না। জানতেন না? নাকি, মানতেন না? বিশেষজ্ঞদের মত বলে – মানতেন না। জানতেন, কিন্তু শূন্যকে সংখ্যা হিসাবে ওঁরা মানতেন না।

শূন্য দিয়ে ফাঁক বোঝাই

মেসোপটেমিয়া তথা ব্যাবিলনিয় সভ্যতার গণিত ঘরানার স্বাভাবিক উত্তরাধিকারী ছিলেন গ্রীক সভ্যতার দিকপালেরা্‌, যারা সমগ্র মানবজাতির জ্ঞান-বিজ্ঞান-দর্শন চর্চার ইতিহাসে অন্যতম পুরোধা পুরুষ ছিলেন। আর ব্যাবিলনিয়রা খ্রিস্টজন্মের প্রায় চারশো বছর আগেই ঠেকে শিখেছিলেন শূন্যের গুরুত্ত্ব! ওঁদের সংখ্যাপাতন পদ্ধতি ছিল ষষ্টিক, অর্থাৎ পরিভাষায় সেক্সাজেসিমাল, মানে ষাট এর এককে স্থানীয়মান-ভিত্তিক। অর্থাৎ ওদের সংখ্যা-চিহ্নের দুটো ১-কে পাশাপাশি লিখলে তার মানে বোঝাতো ১×৬০+১, অর্থাৎ একষট্টি, আমাদের মতন এগারো নয়।

প্রাথমিক পর্যায়ে হাজার খানেকেরও অনেক বেশী বছর কোন শূন্য ছিলনা এই পদ্ধতিতে। ফলে প্রায়ই পড়তে হতো গভীর গাড্ডায়। ব্যাপারটা বুঝতে আজকের দশমিক সংখ্যাতন্ত্র ব্যবহার করে একটা সমান্তরাল সমস্যার কথা বলি। ধরুন ‘শূন্য’ নেই। তাহলে এগারো আর একশো একের তফাৎ করবেন কি করে? অথবা এক হাজার এক? ব্যাবিলনিয়রা যা করতেন (প্রাক সেলুসিড যুগে ৩১২-৬৩ খ্রিস্টপূর্বাব্দে) তা করলে লিখতে হবে যথাক্রমে ১১, ১ ১ এবং ১ ১।

বুঝুন ব্যাপারটা। ফাঁক দিয়ে সমস্যা সামাল দেওয়ার চেষ্টা। বুঝতেই পারছেন এর অর্থ বা তাৎপর্য কখনোই অনন্য বা সুনির্দিষ্টভাবে সকলের পক্ষে বোঝা সম্ভব নয়, একমাত্র যে লিখেছে সে বাদে্‌, এমনকি অনেক সময় তার পক্ষেও নয়, বিশেষত যদি ফাঁকটা বেশ বড় হয়!

ফল যা হবার তাই হতো। বিপত্তি, বিভ্রান্তি, হিসেবের গোলমাল। হাজার বছরের বেশী সময় লেগেছিল একথা বুঝতে যে ওই ফাঁককে বোঝাই করতে কোন একটা চিহ্ন লাগবে। মোটামুটি চারশো খ্রিস্টপূর্বাব্দ নাগাদ ব্যাবিলনিয়রা এই ফাঁক বোঝাই করার জন্য এক বিশেষ চিহ্ন ব্যবহার শুরু করেন। মানবসভ্যতার ইতিহাসে এই চিহ্নকেই অনেকে শূন্যের পূর্বপুরুষ বলে অভিহিত করেন।

তবে এই শূন্য আজকের আধুনিক গণিতের শূন্য নয়, চেহারাতেও নয়, গাণিতিক ধর্মেও নয়। বস্তুত স্থানীয়মান পদ্ধতিতে শূন্যের দুটো ভূমিকা থাকে। একটা হলো এই ফাঁক বোঝাই করা, যাকে পরিভাষায় বলে প্লেসহোল্ডার শূন্য – যার কাজ হোল অন্য সংখ্যা চিহ্নদের ঠেলে ঠুলে নিজের “স্থানে” বা নিজের ঘরে পাঠানো; যেমন ১০১ বা ১০০১-এর বেলায় শূন্যের ব্যবহার। আর দ্বিতীয়টা হলো অন্য যেকোনো সংখ্যার মত নিজের জোরে সংখ্যা হিসেবে তার পরিচয়, যেমনটা হয় ২-২ = ০ হলে। শূন্যের এই দ্বিতীয় চরিত্র ‘ব্যাবিলনিয় শূন্যে’ ছিলনা। ওই বিশেষ শূন্য-চিহ্ন শুধুই প্লেস হোল্ডার হিসেবে ব্যবহৃত হত। কিন্তু তাহলেও এই শূন্যের ধারণার এই প্রাথমিক বীজ নিশ্চিতভাবেই ব্যাবিলনিয়দের হাত ঘুরে পৌঁছেছিল গ্রিক সভ্যতায়। অসামান্য গ্রিক পণ্ডিতদের হাতে তার পূর্ণ বিকাশ ঘটাই ছিল স্বাভাবিক। কিন্তু তা হয়নি।

শূন্যের প্রতি গ্রীক দার্শনিকদের তীব্র অনীহা

টলেমী বা থিয়নের মত জ্যোতির্বিদের হাতে নক্ষত্রের অবস্থান নির্ণয়ের কাজে ব্যবহৃত ফাঁক-বোঝাই করার ‘হেলেনিয় শূন্য’ আজকের আধুনিক শূন্য হয়ে উঠতে পারেনি। কেন? তার নানান কৌতূহল জাগানো কারণ রয়েছে।

গ্রিক সভ্যতার জ্যামিতি নির্ভরতা ছিল এর অন্যতম প্রধান কারণ। জ্যামিতি চর্চা ছিল গ্রিক যুগে বিজ্ঞান চর্চার অবিসংবাদী সর্বোচ্চ ধারা। এতোটাই যে, দার্শনিক প্লেটোর জ্ঞানচর্চার আখড়া জিমনাসিয়াম-এর প্রবেশ পথে খোদাই করা ছিল: জ্যামিতি-অজ্ঞদের প্রবেশ নিষেধ। প্রত্যেকটা (ধনাত্মক) পূর্ণসংখ্যাকেই কল্পনা করা হত এক বা একাধিক জ্যামিতিক আকারে – কেউ ত্রিভুজাকার, কেউ চতুর্ভুজাকার, কেউ বা পঞ্চভুজাকার ইত্যাদি। প্রশ্ন উঠেছিল শূন্যের আকার কি হবে? কোন ধরনের জ্যামিতিক চিত্রের সাথে জড়িয়ে ভাবা যাবে এই প্রস্তাবিত ‘সংখ্যা’ কে? সাথে যোগ হয়েছিল দার্শনিক জটিলতা। শূন্য মানে যদি ‘কিছুই নয়’, তবে যা ‘কিছু নয়’ তাকে আবার কোনোকিছু দিয়ে বোঝানো যায় নাকি? বোঝাতে যাওয়া কি অযৌক্তিক হবেনা?

ইতিমধ্যে পাইথাগরাস আবিষ্কার করে ফেলেছেন দুটো সংখ্যার অনুপাতের ধারণা। একতারা (মনোকর্ড) বাজাতে গিয়ে মূল সুর এবং তার অষ্টক (অক্টেভ)-এর খোঁজ পেয়েছেন টানটান করা তারের উপযুক্ত স্থানে দৈর্ঘ্য বিভাজন করে। গাণিতিক অনুপাতের এমন চমৎকার প্রয়োগ খুঁজে পেয়ে উল্লসিত পাইথাগরাস একে কাজে লাগিয়ে ঘোষণা করেছেন তার নিজস্ব বিচিত্র বিশ্বতত্ত্ব – All is number। এর মূল বক্তব্য দাঁড়িয়ে আছে সংখ্যার অনুপাতের ধারণার ওপর ভিত্তি করে। এখন যদি শূন্যকে সংখ্যা বলে মানতে হয় তাহলে ত সর্বনাশ! কারণ, কোন সংখ্যার সাথে শূন্যের অনুপাত কি হবে? সমগ্র গণিতের জগতকে তছনছ করে দিতে পারে এই প্রস্তাবিত নতুন সংখ্যা!

এর মধ্যে মহাপণ্ডিত অ্যারিস্টটল আবার ঘোষণা করলেন প্রকৃতিতে শূন্যস্থান বলে কিছু হয়না – ‘nature abhors a vacuum’, এবং এই বিশ্বের সব কিছুই সসীম – সীমাহীন বলেও কিছু হয়না! আর এইসব দার্শনিক কুটকচালির ফাঁদে পড়ে তাবড় গ্রিক জ্যামিতিবিদ তথা গণিতজ্ঞেরা মুখ ফিরিয়ে নিলেন শূন্যের থেকে, আর হ্যাঁ, অসীমতার থেকেও। না হলে আর্কিমিডিস তো প্রায় সমাকলনের (integral calculus) সাহায্যে ক্ষেত্রফল বের করার মতন পদ্ধতি আবিষ্কার করেই ফেলেছিলেন – তবে সে অন্য গল্প।

শূন্যের প্রতি এই গ্রিক অনীহার ঐতিহ্য প্রায় দু’হাজার বছর ধরে বহন করেছিল গোটা ইউরোপ, কারণ চার্চ মাথায় করে রেখেছিলেন টলেমীর ভুকেন্দ্রিক বিশ্বতত্ত্বের ধারণায় পুষ্ট অ্যারিস্টটলীয় দর্শনকে। অ্যারিস্টটলের বিরোধিতা ছিল চার্চের বিরোধিতার সমার্থক। মধ্যযুগে যার শাস্তি হতে পারতো এমনকি মৃত্যুদণ্ড পর্যন্ত! ভাবতে পারেন প্রথম লিখিত আকারে আজকের গানিতিক শূন্যকে (যার ইংরেজি নাম ‘zero’) যে ইউরোপীয় বইতে পাওয়া যায় সেটা মোটে ১৪৯১ সালে লেখা! ল্যাটিন-এ লেখা সেই বইয়ের নাম ছিল ‘দি আরিথমাতিকা অপুস্কুলাম’ (De Arithmetica opusculum)। এমনকি একসময় এই শূন্য সহ দশমিক সংখ্যাকে আইন করে নিষিদ্ধ করাও হয়েছিল ইউরোপের কোন কোন অঞ্চলে। রাষ্ট্রের বিরুদ্ধে গিয়ে, সঙ্গোপনে এই সংখ্যাতন্ত্র কে ব্যবহার করতেন তখনকার ব্যবসায়ীরা – কারণ এতে হিসেব করা ছিল অনেক সোজা – রোমান পদ্ধতির মত তা দুরূহ নয়। কি করে এইসব দুর্দিন কাটিয়ে উঠে স্ব-মহিমায় প্রতিষ্ঠিত হয়েছিল শূন্য, সেই কাহিনী কোন উপন্যাসের থেকে কম রোমাঞ্চকর নয়।

শূন্য নিয়ে অধ্যাপক মুখোপাধ্যায়ের বক্তৃতা:

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/zero-01

print