30-10-2024 12:34:39 pm

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

উলট পুরাণ: বস্তুর উল্টে যাওয়ার বিজ্ঞান

সৌরভ কান্তি দে

(মিরগোদা মৃত্যুঞ্জয় বাণীপীঠ)

প্রদীপ্ত পঞ্চাধ্যায়ী

(কাঁথি প্রভাত কুমার কলেজ)

19 May 2023

Link: https://bigyan.org.in/why-things-overturn

%e0%a6%89%e0%a6%b2%e0%a6%9f-%e0%a6%aa%e0%a7%81%e0%a6%b0%e0%a6%be%e0%a6%a3-%e0%a6%ac%e0%a6%b8%e0%a7%8d%e0%a6%a4%e0%a7%81%e0%a6%b0-%e0%a6%89%e0%a6%b2%e0%a7%8d%e0%a6%9f%e0%a7%87-%e0%a6%af%e0%a6%be

আচমকা আমাকে পেছন থেকে ঘাড়ধাক্কা দিলে কী হবে? সোজা দাঁড়ানো অবস্থায় সরসর করে পিছলে সামনে সরে যাবো কি? নাকি একই জায়গায় হুমড়ি খেয়ে পড়বো? নিশ্চয় দ্বিতীয়টা। কিন্তু আমার বদলে একটা কাঠের মোটাসোটা চৌকো বাক্সকে একই ঠেলা মারলে সে কিন্তু হুমড়ি খাবে না, সরেই যাবে। এইসব খুব গুরুত্বপূর্ণ প্রশ্ন নিয়ে মাথা চুলকোচ্ছিলো রাহুল। সৌভাগ্যবশতঃ হাতের কাছেই ছিলেন তার ফিজিক্স টিচার বড়মামা। কখন একটা জিনিস পাল্টি খায় আর কখন সরে যায় সেইটা সহজ কিছু অঙ্ক কষে একদম ঠিকঠিক বাতলে দিলেন তিনি। চলো তাঁদের মধ্যে কী কথা হলো আড়ি পেতে শুনি।

পড়ার টেবিলে জলের বোতলটা হাতে ধাক্কা লেগে উল্টে পড়ল। রাহুল ব্যাপারটা লক্ষ্য করল। সে বোতলটা তুলে রাখল। কয়েকবার বোতলের নীচ থেকে বেশ খানিকটা উপরে ঠেলা দিল এবং দেখা গেল সহজেই বোতলটা উল্টে পড়ছে। রাহুলের মাথায় রোখ চেপে গেল। আস্তে আস্তে বোতলের গা বেয়ে ও হাত নীচে নামাতে থাকল, আর প্রতিবারে বোতলটা ঠেলতে লাগল। এবার দেখল, টেবিলের ওপর থেকে বোতলের একটি নির্দিষ্ট উচ্চতার নীচে যে কোনো জায়গায় বোতলটাকে ঠেলা মারলে বোতলটা আর আগের মত উল্টে যাচ্ছে না। বরং সামনের দিকে এগিয়ে যাচ্ছে। মাথায় চেপে বসল ভাবনা: কেন এমন ঘটছে?

ভাবতে গিয়েই কেমন যেন সব তালগোল পাকিয়ে গেল। কাল বিলম্ব না করে রাহুল সটান ছুটে গেল বড় মামার কাছে। পাশের ঘরেই ছিলেন বড় মামা। তিনি আবার একটা হাই স্কুলের ফিজিক্সের শিক্ষক। বড়দিনের ছুটিতে কালই রাহুলদের বাড়িতে পৌঁছেছেন। বড় মামা রাহুলের ধাত চেনেন। রাহুলকে জিজ্ঞেস করেই বসলেন —- কি ভাগ্নে আবার কী সমস্যা হল?

রাহুল – না, মামা আসলে পড়তে পড়তে হঠাৎ আমার হাতটা বোতলের মাথায় লেগে বোতল উল্টে পড়ল। তারপর আমি বোতলের মাথার দিকে কয়েকবার ঠেলে দেখলাম বোতল সহজে উল্টে যাচ্ছে, কিন্তু নীচের দিকে ঠেলতে বোতল না উল্টে সামনের দিকে এগিয়ে যাচ্ছে। এই ব্যাপারটা কেন হচ্ছে আমি ঠিক ধরতে পারছি না তুমি যদি একটু বুঝিয়ে বলতে।

মামা – চল তোর পড়ার টেবিলে। সেখানেই ব্যাপারটা নিয়ে আলোচনা করি।

দুজনেই পড়ার টেবিলে চলে এল। দুটি চেয়ারে বসে পড়ল। রাহুল খাতা কলম মামার দিকে বাড়িয়ে দিল।

মামা – আচ্ছা বলতো! বোতলে যখন ঠেলা হচ্ছে না, তখন বোতলে কী কী বল কাজ করছে?

রাহুল – দুটো বল কাজ করছে। একটা হল বোতলের ওজন যা বোতলের ভারকেন্দ্র বরাবর নীচের দিকে কাজ করছে। অন্যটা কাজ করছে ঠিক উল্টো দিকে। তা হল টেবিল দ্বারা বোতলের ওপর লম্ব প্রতিক্রিয়া।

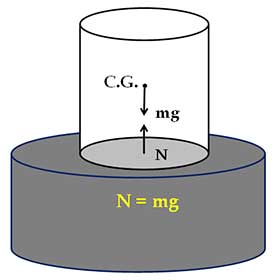
চিত্র ১: গোল টেবিলের ওপর একটি $m$ ভরের এক বেলনাকার বস্তু। $N$ হল লম্ব প্রতিক্রিয়া।

মামা– ঠিকই বলেছিস। আর দেখ, এই দুটো বল মিলে কেমন বোতলের একটা সাম্যাবস্থা তৈরি করেছে। অর্থাৎ, এক্ষেত্রে লম্ব প্রতিক্রিয়া $(N)$ = ওজন ( $mg$ )। এক্ষেত্রে আরেকটা কথা বলি, লম্ব প্রতিক্রিয়াও কিন্তু ভারকেন্দ্রের মধ্য দিয়ে ক্রিয়া করে।

রাহুল – হ্যাঁ মামা, বুঝতে পারছি ।

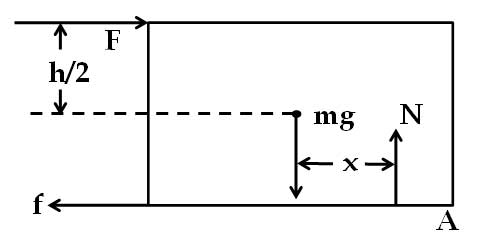
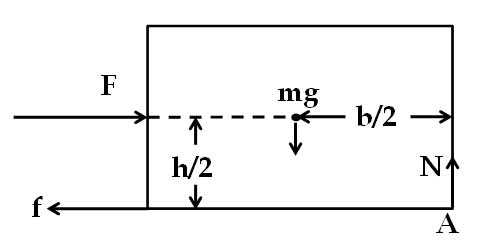
মামা – এবার মনে কর, বোতলের সবচেয়ে উপরের কোনো এক বিন্দুতে একটা বল $F$ দিয়ে তুই বোতলটাকে ঠেলছিস। কিন্তু বোতলটা সরছেও না কিংবা বাঁকছেও না। বোঝার সুবিধার জন্য এখানে বোতলের জায়গায় আমি একটা আয়তাকার বস্তু নিচ্ছি। আর একটা ছবি আঁকছি। ছবিটার দিকে লক্ষ্য কর (চিত্র ২)।

এক্ষেত্রে খুব স্বাভাবিক যে, বোতল ও টেবিলের স্পর্শতলে স্থিত ঘর্ষণ বল ( $f$ ), $F$ বলের বিপরীতে কাজ করে। আর সাম্যাবস্থায় এই দুটি অনুভূমিক বল সমান ও বিপরীতমুখী। যখন উপরের ঠেলা বলটা বস্তু ও মেঝের সীমাস্থ ঘর্ষণ এর থেকে কম, তখনও তো স্থিত ঘর্ষণ ঠেলা বলের মানের সমান হয়। কিন্তু এদের ক্রিয়ারেখাগুলির মাঝে একটা ফাঁক থেকে যায়। ফলে ভারকেন্দ্রের সাপেক্ষে এই দুটি বলের জন্য বস্তুর মধ্যে ঘড়ির কাঁটার দিকে একটি ঘূর্ণন প্রবণতা জন্মায়। সে ক্ষেত্রে একটা কিন্তু টর্ক তৈরি হচ্ছে।

রাহুল – হ্যাঁ, তা ঠিক। কিন্তু উল্লম্ব বলের কথা তুলছো না কেন? আর একটু খুলে বলো প্লিজ।

মামা – আরে, আসছি রে বাবা। যদি উল্লম্ব বলের কথা ধরি, ভারকেন্দ্রের সাপেক্ষে বস্তুর নিম্নমুখী ওজন ( $mg$ ) কোনো টর্ক সৃষ্টি করে না। সাম্যাবস্থায় লম্ব প্রতিক্রিয়া $(N) = mg$ বলতে পারি। আচ্ছা! এবার ধর, এই $F$ বল তুই আস্তে আস্তে বাড়াতে থাকলি। এখন বস্তুকে উল্টাতে না দিলে ভারকেন্দ্রের সাপেক্ষে ঘড়ির কাঁটার দিকের টর্ককে প্রশমিত করতে হবে। এর জন্য ঘড়ির কাঁটার বিপরীতে একটা টর্ক এর প্রয়োজন হয়। তার জন্যই লম্ব প্রতিক্রিয়াকে $(N)$ ডানদিকে সরতে হয়। ঠিক তো?

রাহুল – না ! তাও পুরো বুঝলাম না।

মামা – আচ্ছা একটু অঙ্কের ভাষায় বলি,

রৈখিক সাম্যাবস্থার জন্য, $N = mg$ এবং $F = f$ .

কৌণিক সাম্যাবস্থার জন্য, ভারকেন্দ্রের সাপেক্ষে সমস্ত বলের ভ্রামকের লব্ধি শূন্য।

দুইদিকে বলগুলির ভ্রামক (চিত্র ২) মনে মনে ভেবে নিলে বলতে পারি,

$- F \cdot (h/2) - f \cdot (h/2) + N \cdot x = 0$ যেখানে $x$ হচ্ছে লম্ব প্রতিক্রিয়ার সরণ। এখানে ঘড়ির কাঁটার দিকে টর্ক ‘-‘ চিহ্ন দ্বারা বোঝানো হয়েছে, আর ‘+’ চিহ্ন প্রয়োগ করা হয়েছে ঘড়ির কাঁটার বিপরীত দিকের টর্কের ক্ষেত্রে। বা, $x = Fh/N = Fh/mg$ ।

চিত্র ২:একটি আয়তঘনাকার বস্তুর চূড়োয় (ভারকেন্দ্র থেকে $h/2$ উপরে) প্রযুক্ত $F$ বল বাড়ানোয় লম্ব প্রতিক্রিয়া ভারকেন্দ্র থেকে বস্তুর প্রান্তবিন্দু $A$ এর দিকে সরে যাচ্ছে। $f$ ঘর্ষণবল।

চিত্র ২:একটি আয়তঘনাকার বস্তুর চূড়োয় (ভারকেন্দ্র থেকে $h/2$ উপরে) প্রযুক্ত $F$ বল বাড়ানোয় লম্ব প্রতিক্রিয়া ভারকেন্দ্র থেকে বস্তুর প্রান্তবিন্দু $A$ এর দিকে সরে যাচ্ছে। $f$ ঘর্ষণবল।

রাহুল – এইবার বুঝলাম। তাহলে ঠেলা বল এর মান যত বাড়বে $N$ ক্রমশ ডান দিকে সরে যাওয়ার কথা। আর শেষ পর্যন্ত কি $N$ একেবারে ডান দিকের প্রান্তরেখা বরাবর কাজ করবে?

মামা – আরেব্বাস ! জিও ভাগ্নে। সত্যিই তাই। ঠেলা বল এর মান ক্রমশ বাড়তে থাকলে $N$ ক্রমশ ডান দিকে সরতে সরতে শেষ পর্যন্ত প্রান্তবিন্দু $A$ বরাবর একেবারে খাড়া উপরের দিকে কাজ করবে।

রাহুল – মামা ! মামা ! এক মিনিট দাঁড়াও। আচ্ছা তাহলে প্রান্তবিন্দু $A$ ধরে হিসেব করলে $x$ এর মান কি একই বেরোবে?

মামা – আমি বলব না। হিসেবে কর।

রাহুল – হোক। তথাস্তু ! $A$ বিন্দুর সাপেক্ষে যদি টর্কের হিসেব (চিত্র ২) করতে চাই তাহলে প্রথমে লিখি, ঐ বিন্দুর সাপেক্ষে সমস্ত বলের ভ্রামকের লব্ধি শূন্য।

$- F \cdot h - N \cdot (b/2 - x) + mg \cdot (b/2) = 0,$

$N$ এর মান সেই $mg$ বসালে ফল গিয়ে দাঁড়াল, $x = Fh/mg$ . চমৎকার রেজাল্ট কিন্তু বেরোল মামা। এবার একটু কেমন যেন নিজের ওপর একটু গব্ববোধ হচ্ছে।

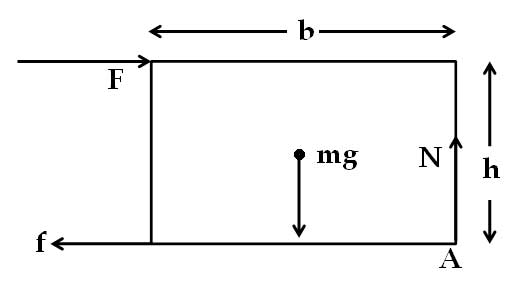
মামা – বেড়ে পাকা হয়েছিস তুই। যাইহোক, একটা দিক খেয়াল কর। এখনো আমরা ধরছি যে বস্তুটির সরণ নেই এবং তা টেবিলের ওপর লম্বভাবে বসে আছে। এরপর যদি ঠেলা বলটিকে আমরা বাড়াই, লম্ব প্রতিক্রিয়া ডানদিকে আরও সরে যাওয়ার উপায় থাকে না। তখন ঠেলা বলের জন্য ঘড়ির কাঁটার দিকে যে টর্ক সৃষ্টি হয়, তার জন্য বস্তু A বিন্দুর সাপেক্ষে পাল্টি খেয়ে যায়।

তাই এই সাম্য অবস্থা (চিত্র ৩) বিবেচনায় আনলে সেই আবার লিখতে পারি: $F = f$ ও $N = mg$ এবং $A$ (প্রান্ত) বিন্দুর সাপেক্ষে সমস্ত বলের ভ্রামকের লব্ধি শূন্য। আর এক্ষেত্রে ঠিক আগের সমীকরণে (বলগুলির ভ্রামক নিয়ে তৈরি) $x = x_{max} = b/2$ বসিয়ে পাই, $F_{max} = mgb/2h$ .

চিত্র ৩: উল্টে যাওয়ার ক্ষেত্রে প্রযুক্ত ঠেলা বলের সীমামান ( $F_{max}$ ) যার জন্য প্রান্তবিন্দু $A$ তে লম্ব প্রতিক্রিয়া ( $N$ ) এর অবস্থান।

রাহুল – বস্তুর কোনোভাবে নাড়াচাড়া না ঘটিয়ে কি F এই মান অব্দি বাড়ানো যায়?

মামা – একেবারে! এটাই $F$ এর সর্বোচ্চ মান( $F_{max}$ ) যার জন্য $N$ একেবারে ডানদিকের শেষপ্রান্তে সরে যাবে ও প্রান্তরেখা বরাবর কাজ করবে। এবার একটি $F$ এর মান ধরি যা অবশ্যই $mgb/2h$ অপেক্ষা বেশি এবং এক্ষেত্রে টর্কগুলো প্রান্তবিন্দু $A$ এর সাপেক্ষে বিবেচনা করি। যদি $hF$ (ঘড়ির কাঁটার দিকের টর্ক যা বস্তুকে উল্টাতে সাহায্য করে) $> mgb/2$ (ঘড়ির কাঁটার বিপরীত দিকের টর্ক যা বস্তুকে উল্টাতে বাধা দেয়) হয়, তাহলে বস্তু অবধারিতভাবে পাল্টি খেয়ে যায়।

রাহুল – পাল্টি হল বুঝলাম। পিছলে যাওয়ার ঘটনা ঘটা কি সম্ভব? তখন কি ঠেলা বল বস্তু ও মেঝের সীমাস্থ ঘর্ষণের থেকে বেশি হবে?

মামা – আরিব্বাস! এখন তো দারুণ প্রশ্ন করছিস! যাক আমার লক্ষ্য আস্তে আস্তে পূরণ হচ্ছে দেখছি। যাইহোক, কাজের কথায় ফিরি। সীমাস্থ ঘর্ষণের ক্ষেত্রে, $f = \mu mg$ । তাই $F$ এর মান $\mu mg$ অপেক্ষা বেশি হলে বস্তু পিছলে যাবে। এবার যদি $mgb/2h > \mu mg$ হয়, তবে বস্তুটি পাল্টি খাওয়ার আগেই পিছলে যাবে আর যদি $mgb/2h < \mu mg$ হয় বস্তু পিছলে যাওয়ার আগেই পাল্টি খাবে। কিরে বোঝাতে পারছি?

রাহুল – একদম। একটা জিনিস ভাবছি মামা— ঠেলা বলটি যদি সীমাস্থ ঘর্ষণ ( $\mu mg$ ) এবং পাল্টি না খাওয়ার জন্য সর্বোচ্চ বল ( $mgb/2h$ ) দুটোর থেকেই কম হয় তাহলে বস্তু স্থির থাকবে, পিছলে যাওয়া বা পাল্টি খাওয়া কিছুই ঘটবে না। আর একটা ব্যাপার মামা! দেখো $\mu$ এর মান যত বেশি হবে, সীমাস্থ ঘর্ষণ তত বেশি হবে। সেক্ষেত্রে বস্তুর পিছলে যাওয়ার থেকে পাল্টি খাওয়ার সম্ভাবনা কিন্তু বেড়ে যাবে। আবার ( $b/h$ ) অনুপাত যত কম হবে, সীমাস্থ ঘর্ষণ বলের তুলনায় $mgb/2h$ বলের মান‌ও কমে যাবে। এর ফল হচ্ছে বস্তুর পিছলে যাওয়ার আগেই পাল্টি খাওয়ার সম্ভাবনা বাড়তে থাকবে। ঠিক বলছি মামা?

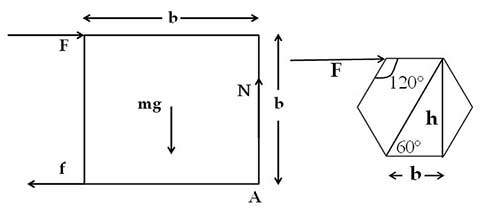
চিত্র ৪: F_maxএর হিসেবে ধরতে হবে – একটি বর্গাকার বস্তুর ক্ষেত্রে b = h, ও একটি সুষম ষড়ভুজাকার বস্তুর ক্ষেত্রে h = b.tan60° = b√3 ।

মামা – দারুণ বুঝেছিস ভাগ্নে। এই যে ব্যাপারটা তুই যেটা অঙ্কের মাধ্যমে ধরে ফেললি সেটা একটু বাস্তবে দেখাই। (চিত্র ৪) একটি বর্গাকার বস্তুর ক্ষেত্রে $b = h$ , তখন $F_{max} = mg/2$ । একটি সুষম ষড়ভুজাকার বস্তুর ক্ষেত্রে, $h = b \cdot tan60^{\circ}= b\sqrt{3}$ , তখন $F_{max} = mg/(2 \sqrt{3})$ । দেখ দ্বিতীয়টির ক্ষেত্রে পাল্টি খাওয়ার জন্য কম বলই লাগছে। বাস্তবেও তুই দেখবি বর্গাকার বস্তুর তুলনায় সুষম ষড়ভুজাকার বস্তুকে সহজে পাল্টি খাওয়ানো যাচ্ছে। এভাবে যত বাহু সংখ্যা বাড়বে তত সহজে বস্তু পাল্টি খাবে। একটা বৃত্তাকার বস্তু, যেমন চাকার কথাই ভাব না! ধরি, মাটির উপরে একটি চাকা দাঁড় করিয়ে রাখা আছে। একটা বৃত্তকে আমরা অসংখ্য অতি ক্ষুদ্র ক্ষুদ্র বাহুর সমন্বয় ভাবতে পারি, অর্থাৎ b এর মান অত্যন্ত কম হয়। সেক্ষেত্রে মাটির সাথে চাকার খুব কম অংশ সংস্পর্শে থাকে, অর্থাৎ এর মান শূন্যের কাছাকাছি হয়। আদর্শ ক্ষেত্রে $b = 0$ বলে ধরতে পারি। আর তার জন্য $F$ এর মানও শূন্য হয়। এর অর্থ দাঁড়ায়, চাকাকে অল্প টোকা দিলেই চাকা গড়াতে শুরু করে দেয়।

রাহুল – মামা, তার মানে যা দাঁড়াল তাতে বলা যায় বিশুদ্ধ গড়ানো হল ক্রমাগত পাল্টি খেয়ে যাওয়া!!

মামা – যা বলেছিস।

রাহুল – আচ্ছা মামা চাকা কি কখনোই পিছলে যাবে না, শুধুমাত্র গড়াবে?

মামা – তা কেন? ঘর্ষণ একেবারেই না থাকলে এবং ভারকেন্দ্র বরাবর ঠেললে চাকা শুধুমাত্র পিছলেই যাবে, একদম গড়াবে না। কেন বুঝতে পারছিস?

রাহুল – হ্যাঁ বুঝেছি। আচ্ছা মামা, এই যে $F_{max}= mgb/2h$ রাশিমালা থেকে তো বলাই যায় যে, $h$ এর মান যত বাড়বে, $F_{max}$ এর মান তত কমবে। অর্থাৎ বস্তুর যত উপরের দিকে ঠেলা হবে বস্তুকে তত বেশি সহজে উল্টানো যাবে। আচ্ছা মামা, যখন একদম বস্তুর ভারকেন্দ্র বরাবর ঠেলা হবে তখন কী হতে পারে?

মামা – অত্যন্ত প্রাসঙ্গিক ভাবনা ভাগ্নে! দেখ, ঠেলা বলটির ক্রিয়ারেখা উপর থেকে যত ভারকেন্দ্রের দিকে নামতে থাকবে, এই বলের জন্য সৃষ্ট ঘড়ির কাঁটার দিকের টর্কও কমতে থাকবে। এর কারণ ভারকেন্দ্র থেকে ঠেলা বলের ক্রিয়ারেখার দূরত্ব কমে যায়। চিত্র ৫ লক্ষ্য কর।

রৈখিক সাম্যাবস্থার জন্য, $N = mg$ এবং $F = f$ ।

ভারকেন্দ্রের সাপেক্ষে কৌণিক সাম্যাবস্থার জন্য,

$- F \cdot y - f \cdot (h/2) + N \cdot (b/2) = 0$

বা, $F(y + h/2) = mg \cdot (b/2)$

বা, $F = mg \cdot (b/2)/(y + h/2)$

অতএব, $F_{max} = mg \cdot b/(2y + h)$ ।

চিত্র ৫: ভারকেন্দ্র থেকে $y$ লম্বদূরত্ব উপরে ঠেলা বল $F$ প্রযুক্ত হচ্ছে। যদি ঠেলা বল ভারকেন্দ্র থেকে $y$ লম্বদূরত্ব নীচে প্রয়োগ করি, তবে $y$ এর চিহ্ন ঋণাত্মক ধরতে হবে।

এবার আমি নিজে থেকেই সন্দেহের নিরসন করে দিই। প্রান্তবিন্দু $A$ এর সাপেক্ষে কৌণিক সাম্য খেয়াল কর।

রাহুল- আরে হ্যাঁ ! এবার বিশারদ হয়ে গেছি।

$A$ এর সাপেক্ষে বলতে পারি, $- F(y + h/2) + mg \cdot (b/2) = 0$

বা, $F(y + h/2) = mg \cdot (b/2)$

তাহলে, $F_{max} = mg \cdot b/(2y + h)$ ।

আবার দেখো মামা, ভারকেন্দ্র ও প্রান্তবিন্দু এই দুইয়ের সাপেক্ষে বস্তুর উল্টানোর জন্য সর্বাধিক বলের রাশিমালা একেবারে সমান। সে হল না হয়! এবার এর ফলশ্রুতি রূপে কী কী দেখতে পাই, সেটা বলো।

মামা – লক্ষ করে দেখ, $mgb/2h$ এর মান অপেক্ষা $mgb/(2y + h)$ এর মান বড় (যেহেতু, $y < h/2$ , বা $2y < h$ )। তার মানে পাল্টি খাওয়ার জন্য সীমাস্থ মান আরও বেড়ে যায়। অর্থাৎ বস্তুর পাল্টি খাওয়ার সম্ভাবনা কমে যায়। আরো লক্ষ কর ঠেলা বল যখন ভারকেন্দ্র বরাবর হয়, অর্থাৎ $y = 0$ তখন $F_{max} = mgb/h$ হয়। এর মানে দাঁড়ায় পাল্টি খাওয়ার জন্য ঠেলা বলের সীমাস্থ মান আরো বেড়ে যায় অর্থাৎ বস্তুর উল্টে পড়ার সম্ভাবনা আগের থেকে আরো কমে যায়।

রাহুল – তার মানে মামা ভারকেন্দ্র বরাবর ঠেললেও বস্তু পাল্টি খেতে পারে।

কিন্তু আমরা যে পড়েছিলাম ভরকেন্দ্র বরাবর বল প্রযুক্ত হলে বস্তুর কেবলমাত্র রৈখিক গতি থাকে, কোনো কৌণিক গতি থাকবে না। তবে এখানে ছোট্ট একটা খটকা মনে আসছিল। আসলে আলোচনাটা শুরু হয়েছিল ভারকেন্দ্র দিয়ে, আবার রৈখিক বা কৌণিক গতির প্রসঙ্গে ভরকেন্দ্রের ধারণাটাও মনে এল। সংশয়টাও দূর করলাম নিজে থেকেই এটা মনে করে যে, ছোটখাটো থেকে মাঝারি মানের সাধারণ বস্তুর ক্ষেত্রে ভরকেন্দ্র ও ভারকেন্দ্র এক জিনিস। যাই হোক, এখানে ভারকেন্দ্র বা ভরকেন্দ্র বরাবর ঠেলা দিলে কৌণিক গতি কী করে সম্ভব হচ্ছে?

চিত্র ৬: ভারকেন্দ্র বরাবর বল প্রয়োগ করলে বলের সাম্য।

মামা – ঠিকই ধরেছিস। কিন্তু একটা ভুল হচ্ছে তোর। সেটা হল— ভারকেন্দ্র বা ভরকেন্দ্র যাই বলিস, তা বরাবর বল প্রয়োগ করলে শুধু রৈখিক গতি সৃষ্টি হয়। তবে যদি ঐ বলটি ছাড়া আর কোনো বল না থাকে। কিন্তু এখানে তো ঠেলা বল ছাড়াও স্থিতঘর্ষণ কাজ করছে। ভারকেন্দ্রের সাপেক্ষে বলগুলির ভ্রামক নিলে কী হয় দেখ এবার,

$- F \cdot 0 - f \cdot (h/2) + N \cdot (b/2) = 0$

$F = f$ ও $N = mg$ বসিয়ে পাই, $F = mgb/h$ ।

আর এর জন্য ভারকেন্দ্রের সাপেক্ষে ঘড়ির কাঁটার দিকে একটা টর্ক থেকে যায়। ফলে এর উপস্থিতির জন্য বস্তু পাল্টি খেয়ে যায়।

রাহুল – ঠিক বলেছো মামা। এটা আমি ভেবে দেখিনি।

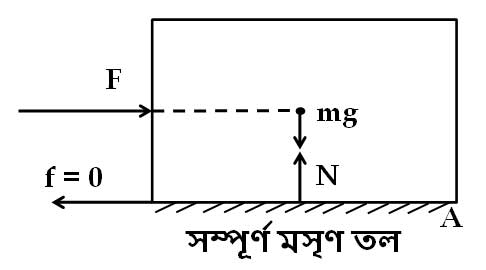
মামা – বেশ এবার তোর কথায় আসি। মনে কর, একেবারে মসৃণ একটি তলে বস্তুকে রেখে ভারকেন্দ্র বরাবর ঠেলা হল। এখন ঘড়ির কাঁটার দিকে মোটের ওপর টর্ক শূন্য হয়। কেন বলতো?

রাহুল – হ্যাঁ বুঝতে পেরেছি। ঠেলা বল তো ভারকেন্দ্র বরাবর কাজ করে। ভারকেন্দ্রের সাপেক্ষে এর ভ্রামক শূন্য। আবার তল একেবারে মসৃণ হওয়ায় এখানে ঘর্ষণও কাজ করে না। তাই ভারকেন্দ্রের সাপেক্ষে মোট টর্ক শূন্য।

মামা – বাহ! তাহলে লম্ব প্রতিক্রিয়া ও ভারকেন্দ্র বরাবর ঊর্ধ্বমুখী হবে, ডানদিকে সরার প্রয়োজন হয় না। দেখ বস্তুর শুধু ঠেলা বলের জন্য রৈখিক গতিই থাকে। ভারকেন্দ্রের ধারণাটা এবার মেলাতে পারছিস।

চিত্র ৭: সম্পূর্ণ মসৃণ তলে ভারকেন্দ্র বরাবর $F$ বল দিলে কেবল রৈখিক গতির সৃষ্টি।

রাহুল – হ্যাঁ মামা। এবারে জলের মত পরিষ্কার হল বিষয়টা।বেশ কিছুক্ষণ চুপ থাকার পর রাহুল আবার জিজ্ঞাসা করল— মামা, বস্তুকে ভারকেন্দ্রের নীচের কোনো বিন্দু বরাবর ঠেললে কী হবে?

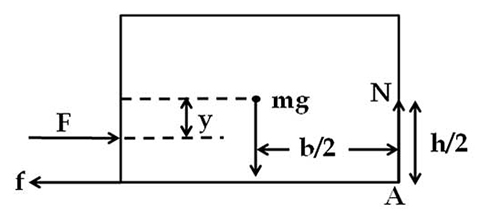
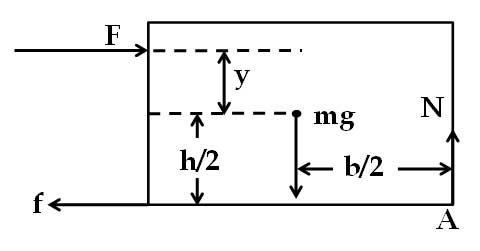
চিত্র ৮: ভারকেন্দ্র থেকে $y$ দূরত্ব নীচে $F$ বল প্রযুক্ত হলে বলগুলির বিন্যাস।

মামা – বাহ! পর পর বেশ প্রশ্ন বেরোচ্ছে ! মনে কর, ভারকেন্দ্র থেকে কিছুটা ( $y$ ) দূরত্ব নীচে ঠেলা বল $F$ দেওয়া হল। এক্ষেত্রেও রৈখিক সাম্যাবস্থার জন্য $F = f$ এবং $N = mg$ হয়। কৌণিক সাম্যাবস্থার জন্য ভারকেন্দ্রের সাপেক্ষে নেট বলের ভ্রামক শূন্য হবে। তাই,

$F \cdot y - f \cdot (h/2) + N \cdot x = 0$

বা, $x = F \cdot (h/2 - y)/N= F \cdot (h/2-y)/mg$ ।

$y$ এর মান $h/2$ এর চেয়ে কম হওয়ায়, $F$ এর মান বাড়াতে থাকলে $x$ এর মান ক্রমশ বাড়তে থাকবে অর্থাৎ লম্ব প্রতিক্রিয়া ভারকেন্দ্রের সাপেক্ষে ডানদিকে সরতে থাকবে কিন্তু আগের থেকে কম দূরত্বে সরবে। এভাবে লম্ব প্রতিক্রিয়া সরতে সরতে একেবারেই ডানপ্রান্তে থাকলে ( $A$ বিন্দুতে) অর্থাৎ $x = b/2$ হলে, $A$ বিন্দু সাপেক্ষে কৌণিক সাম্যব্যবস্থা বিবেচনা করলে দাঁড়ায়,

$F \cdot (h/2 - y) = mg \cdot b/2$

তাই, $F_{max} = mgb/(h - 2y)$ ।

বুঝতেই পারছিস, বস্তুকে উল্টানোর জন্য আগের থেকে আরো অনেক বেশি বল দিয়ে ঠেলতে হবে। এর অর্থ, বস্তুর পাল্টি খাওয়ার সম্ভাবনা আগের থেকে অনেকটাই কমে যাচ্ছে। অন্যদিকে সীমাস্থ ঘর্ষণের ( $\mu mg$ ) মানের কিন্তু কোনো পরিবর্তন হচ্ছে না। সাধারণত $\mu$ এর মান $1$ এর থেকে কম হয়, আর সাধারণ বস্তুগুলোর ক্ষেত্রে $b/(h-2y)$ এর মান $1$ এর কাছাকাছি বা তার বেশি হয়ে যায়। সুতরাং, $F_{max} = mgb/(h - 2y)$ বলটি সীমাস্থ ঘর্ষণ থেকে বেশ খানিকটা বেশি হওয়ায় এই ক্ষেত্রে বস্তুকে ঠেললেই বস্তু পিছলে যাবে। অন্যদিকে, খুব লম্বাটে বস্তুর ক্ষেত্রে যখন $\mu > b/(h-2y)$ হয় তখন কিন্তু বস্তুকে ঠেললে বস্তু পাল্টি খাবে। (ভাবা যেতে পারে, উচ্চ ঘর্ষণযুক্ত তল $\mu$ এর মান $1$ এর কাছাকাছি আর বেশ লম্বাটে বস্তু যার ক্ষেত্রে $b < (h-2y)$ হয়।

এখন যদি একেবারে স্পর্শতল বরাবর বস্তুকে ঠেলা যায়, অর্থাৎ $y = h/2$ বা, $h = 2y$ হলে $F$ এর মান অনির্ণেয়। সুতরাং বলা যায়, যত বড় মাপের বল দিয়ে স্পর্শতল বরাবর বস্তুকে ঠেলে থাক না কেন, কোনোভাবেই উল্টানো যাবে না। এক্ষেত্রে ঘর্ষণ যতই বাড়ুক এবং বস্তু যতই লম্বা হোক, বস্তু কেবলই পিছলে যাবে।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/why-things-overturn

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম An online Bengali Popular Science magazine

https://bigyan.org.in

উলট পুরাণ: বস্তুর উল্টে যাওয়ার বিজ্ঞান

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine