30-12-2024 16:52:06 pm

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

বিশৃঙ্খলার গতিবিদ্যা

জয়ন্ত ভট্টাচার্য

(IACS)

22 Oct 2018

Link: https://bigyan.org.in/uncertainty-in-dynamics

%e0%a6%ac%e0%a6%bf%e0%a6%b6%e0%a7%83%e0%a6%99%e0%a7%8d%e0%a6%96%e0%a6%b2%e0%a6%be%e0%a6%b0-%e0%a6%97%e0%a6%a4%e0%a6%bf%e0%a6%ac%e0%a6%bf%e0%a6%a6%e0%a7%8d%e0%a6%af%e0%a6%be

আবহাওয়ার পূর্বাভাস তো অঙ্ক কষেই দেওয়া হয়। এ কেমনধারা অঙ্ক যেখানে কোনো নিশ্চয়তা নেই?

আমাদের ছোটবেলায় আবহাওয়া অফিসে যাঁরা কাজ করতেন, তাদের নিয়ে ঠাট্টা তামাশার অন্ত ছিল না। রেডিওতে (যন্ত্রটি আজকাল আর দেখা যায় না) যেই শোনা যেত “আবহাওয়ার পূর্বাভাস বলা হচ্ছে …”, অনেক শ্রোতা রেডিও বন্ধ করে দিতেন অথবা খোলা রাখতেন মন্তব্য করার জন্য। “গাঁজায় দম দিয়ে এসেছেন”, “এখানকার আবহাওয়াটা ওর মাথার জন্য ভালো নয়”, ইত্যাদি শুনতে খুব মজাই লাগতো। অর্ধ শতকেরও বেশি পরে বুঝতে পেরেছি তাদের কোনো দোষ ছিল না। তাদের দেওয়া হয়েছিল তখনকার দিনের একটা প্রায় অসম্ভব কাজ। তাঁদের কাজটা কেন এত কঠিন ছিল, সেটাই এই লেখায় বোঝানোর চেষ্টা করবো।

নিউটনের সূত্রের সমীকরণ

ধরা যাক, আমি $980cm/s$ গতিতে সরাসরি উপরের দিকে একটা ছোট নুড়ি ছুঁড়ে দিলাম। আমি জানতে চাই কতক্ষণ পর সেই নুড়িটা আমার হাতে এসে পড়বে। নিউটন-এর সূত্রের সাহায্যে এর উত্তর বার করতে সকলেই জানে। নুড়িটির ভর যদি $m$ হয়, তাহলে উপরে ওঠার সময় নিউটন-এর দ্বিতীয় সূত্র অনুযায়ী:

$m \frac{dv}{dt} = m \frac{d^2z}{dt^2} = -mg$

সমীকরণের শেষে রয়েছে নুড়িটির ওপর মাধ্যাকর্ষণ বল। বলের সাথে মাইনাস চিহ্ন দেওয়া হলো কারণ আমাদের কোঅর্ডিনেট সিস্টেম (coordinate system) এমন যে আমার থেকে নুড়ির দূরত্ব ( $z$ ) উপর দিকে বাড়ছে। যে সমীকরণটি লেখা হলো, তাকে বলে অবকল সমীকরণ (differential equation)। গতিবিধির বর্ণনা সচরাচর এই অবকল সমীকরণের মাধ্যমেই করা হয়। উপরের সমীকরণটার সমাধান সকলেরই জানা:

$v(t) = v(0) - gt$

$z(t) = v(0)t - \frac{1}{2} gt^2 + z(0)$

যেখান থেকে নুড়িটি ছোঁড়া হলো, সেই বিন্দুটিকে কোঅর্ডিনেট সিস্টেম-এর মূলবিন্দু $z(0) = 0$ বললে আর যেহেতু আমাদের দেওয়া আছে $v(0) = 980cm/s$ , অতএব:

$v(t) = 980 - gt$

$z(t) = 980t - \frac{1}{2} gt^2$

নুড়িটি ততক্ষণ উপরে উঠবে যতক্ষণ না তার গতিবেগ শূন্য হয়ে যাচ্ছে। আমরা জানি $g$ -এর মান $980cm/s^2$ , তাই গতিবেগ শূন্য হবে $t= 1s$ -এর মাথায় এবং তখন নুড়ির উচ্চতা:

$z = 980 - \frac{1}{2} 980= 490cm$

গতিবেগ শূন্য হয়ে গেলে সে মাধ্যাকর্ষণের জন্য নেমে আসতে শুরু করবে। এখনো $v(t)$ আর $z(t)$ -র সমীকরণগুলো প্রযোজ্য কিন্তু এবার $z(0)= 490cm$ এবং $v(0)= 0$ । আমাদের জানবার বিষয় কখন $z(0)= 0$ হবে, অর্থাৎ নুড়িটি আমার হাতে ফিরে আসবে। $z(t)$ -র সমীকরণটি ব্যবহার করলে

$0= -490 t^2 + 490$

যার থেকে পাই

$t= 1s$

আমি ছুঁড়ে দেওয়ার $1+1= 2s$ পরে নুড়িটি আবার আমার হাতে ফিরে আসবে। $v(t)$ -র সমীকরণ অনুযায়ী $t= 1$ -এ নুড়িটির গতিবেগ $980cm/s$ নিচের দিকে, অর্থাৎ একই গতিবেগ (কিন্তু পরিবর্তিত চিহ্ন) নিয়ে নুড়িটি ফিরে আসবে।

শুরুর মাপের ভুলচুকে সমীকরণের প্রভাব

আমি ইচ্ছে করে নুড়িটি $980cm/s$ গতিতে ছুঁড়েছিলাম যাতে সে ঠিক দু’সেকেন্ড পরে আমার হাতে ফিরে আসতে পারে। নুড়িটি যে আমি $980cm/s$ গতিবেগে ছুঁড়েছি সেটা জানার জন্য আমার গতিবেগ মাপার যন্ত্র লেগেছিল। সমস্ত যন্ত্রের একটা সীমাবদ্ধতা (margin of error) আছে — ধরা যাক আমার যন্ত্রের সীমাবদ্ধতা $1\%$ – অর্থাৎ $980cm/s$ এবং $989.8cm/s$ -এর মধ্যে সেই যন্ত্র তফাৎ করতে পারে না। অতএব এটা হতেই পারে যে আমি ভাবলাম সঠিক $980cm/s$ -এ ছুঁড়েছি কিন্তু আসলে নুড়িটির গতিবেগ ছিল $985/s$ । তাহলে নুড়িটি $2s$ পরে না ফিরে $2\frac{985}{980}s$ , অর্থাৎ $2.012s$ পরে ফিরবে। প্রথমে অনিশ্চয়তা ছিল $0.5\%$ , এবং নিউটনের দ্বিতীয় সূত্রের সমীকরণ এমনই একটা সমীকরণ যার শুরুর মাপজোখে $0.5\%$ অনিশ্চয়তা থাকলে, শেষেও ঐ $0.5\%$ অনিশ্চয়তাই থাকছে। সাধারণত আমরা গতিবিদ্যায় যেসব অঙ্ক কষি তাতে শুরুর মাপজোখে সামান্য ভুলের মাশুল বিশাল আকার ধারণ করে না।

ধরা যাক নুড়িটির ওপরে ওঠা এবং নীচে নামাটা নিউটনের দ্বিতীয় সূত্রের সমীকরণের পরিবর্তে এমন কোনো সমীকরণ দিয়ে বর্ণিত হত যার জন্য সামান্য ভুলের মাশুল সামান্য নয়। এমন যদি হত যে $980cm/s$ -এর পরিবর্তে যন্ত্রের ভুল বশতঃ আমি $985cm/s$ -এ ছুঁড়েছি এবং তার চলন এমন যে $980cm/s$ -এ ছুঁড়লে $2s$ পরে ফেরত আসে কিন্তু $985cm/s$ -এ ছুঁড়লে $200s$ পরে ফেরত আসবে? তাহলে কি ঘটতে পারত? আমি অংক করবো $980cm/s$ অনুযায়ী এবং আশা করব $2s$ পরে ফেরত আসবে। নুড়ি কিন্তু চলবে $985cm/s$ অনুযায়ী। দুই সেকেন্ড পেরিয়ে গেলে নুড়ি ফিরল না দেখে আমি যখন মাথার চুল ছিঁড়তে বাকি রেখেছি তখন নুড়ি এসে পড়বে আমার মাথার ওপর!

আমাদের সৌভাগ্য যে নুড়ির জন্য যে গতিসূত্র, অর্থাৎ নিউটনের দ্বিতীয় সূত্র, তাতে এই ধরণের কোনো সমস্যা নেই। কিন্তু বায়ুমণ্ডলের যে গতি-সংক্রান্ত সমীকরণ, অর্থাৎ হাওয়ার দ্রুতি, বায়ুচাপ, আর্দ্রতা ইত্যাদির সময়ের সাথে পরিবর্তন বর্ণনা করার জন্য যে “নিউটনের সূত্র” প্রযোজ্য, সেগুলো ব্যবহার করলে এই দুর্ভোগের সম্মুখীন হতে হয়। এই কারণে আজ থেকে চল্লিশ পঞ্চাশ বছর আগে আবহাওয়াবিদদের কাজটা ছিল প্রায় অসম্ভব। কারণ অবকল সমীকরণগুলোর এই ধর্মটা — শুরুর মানগুলোতে সামান্য ভুল থাকলেও আখেরে ভুলের পরিমাণ বিশাল হয়ে যায় অর্থাৎ কিনা সমীকরণের সমাধানটা ভয়ঙ্করভাবে শুরুর মানগুলোর উপর নির্ভরশীল। একে বলে প্রাথমিক পরিস্থিতির উপর অতিনির্ভরশীলতা (sensitivity to initial conditions)। এই লেখার বাকি অংশে আমার কাজ হবে একটি অত্যন্ত সহজ উদাহরণের সাহায্যে বুঝিয়ে দেওয়া কিভাবে এই প্রাথমিক পরিস্থিতির উপর অতিনির্ভরশীলতার সৃষ্টি হতে পারে।

প্রাথমিক পরিস্থিতির উপর অতিনির্ভরশীলতার উদাহরণ

চলাফেরার বর্ণনা অবকল সমীকরণ দিয়ে না করে একটু অন্যরকম ভাবে করলে ব্যাপারটা বোঝাতে সুবিধে হবে। এই “অন্যরকম” বর্ণনার আবিষ্কারক অঁরি পোঁয়াকারে (Henri Poincare)। মহাকাশে তিন-চার বা ততোধিক গ্রহতারার চলাফেরার বিশ্লেষণ করতে গিয়ে ১৮৯০ নাগাদ পোঁয়াকারে দেখলেন যে সরাসরি নিউটনের সূত্র লেখা দুরূহ – তাই ঐ দশকে তিনি বার করলেন এক নতুন পদ্ধতি যাকে বলে পোঁয়াকারে ম্যাপ (Poincare map)। ধরা যাক একটা সমতলের ( $X-Y$ plane) ওপর একটি কণার গতিবিধি দেখা হচ্ছে – ঐ কণাটির জন্য নিউটনের সূত্র থেকে শুরু করে তার গতিপথ বার করা কোন কারণবশত অত্যন্ত কঠিন, কিন্তু আমাকে জানতে হবে তার গতিপথের বিশেষত্ব কি। ঐ বিশেষত্ব বোঝার জন্য পোঁয়াকারে বললেন পুরো গতিপথটা দেখার দরকার নেই; কেবলমাত্র একটি বিশেষ সরলরেখার সঙ্গে তার ছেদ বিন্দুগুলিই (intersection) যথেষ্ট।

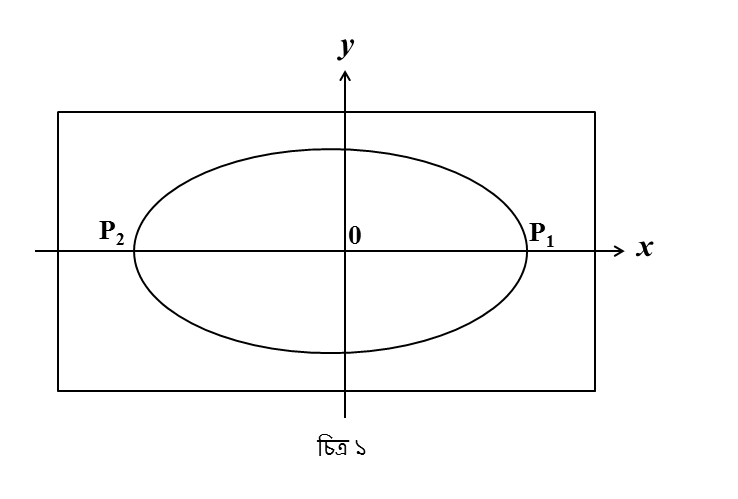
আমাদের পৃথিবী যেমন সূর্যের চারিদিকে একটি উপবৃত্তাকার গতিপথে ঘুরপাক খায়, ঐ কণার গতিপথ যদি সেইরকম হত (চিত্র ১) এবং চিত্রে পূর্বোক্ত সরলরেখাটা যদি হয় $X$ – অক্ষ, তাহলে যদি আমি পোঁয়াকারে-র দৃষ্টিভঙ্গি থেকে দেখি, গোটা উপবৃত্ত ছেড়ে আমি দেখবো শুধু দুটো বিন্দু: $P_1$ ও $P_2$ ।

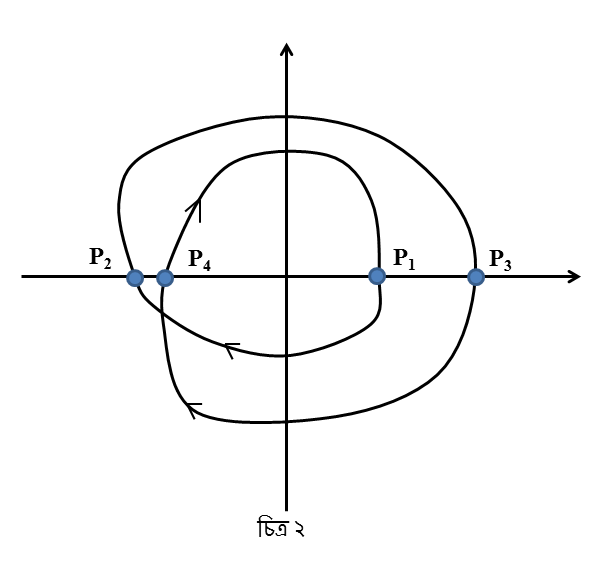
যদি উপবৃত্ত না হয়ে গতিপথটা হত আরও গোলমেলে, যেমন চিত্র ২-এ দেখানো হয়েছে, সেরকম হলে আমি চারটে বিন্দু $P_1, P_2, P_3, P_4$ দেখতে পেতাম।

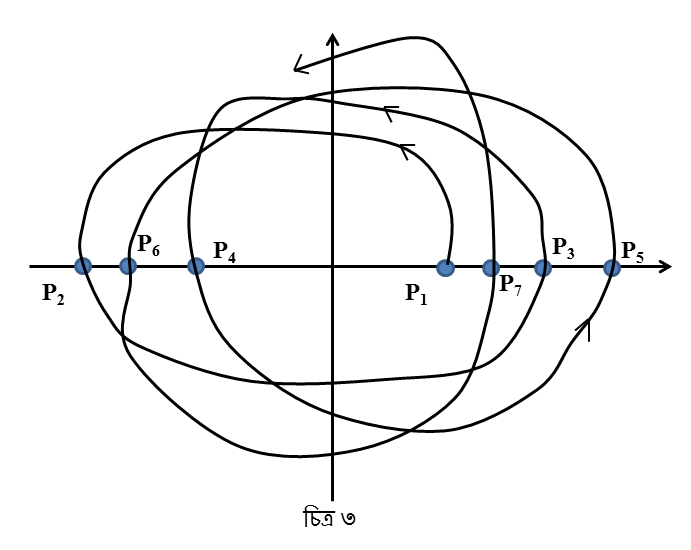
আর যদি এমন হয় যে কক্ষপথ আরও অনেক বেশি অচেনা যেমন চিত্র ৩-এ দেখানো আছে, তাহলে দেখব পরপর কিছু বিন্দু $P_1, P_2, P_3, P_4, P_5, P_6, P_7, \cdots$ ।

প্রথম বিন্দু $P_1$ জানা থাকলে নিউটনের সূত্রের সাহায্যে $P_2$ বেরোবে, $P_2$ জানা থাকলে $P_3$ নির্ণয় করা যাবে এবং এইভাবে এগোনো সম্ভব। পোঁয়াকারে বললেন যে আসলে কক্ষপথটি নির্ণয় করা যখন এত কঠিন তখন $P_1$ থেকে $P_2$ , $P_2$ থেকে $P_3$ না বের করে, কেবল $P_1, P_2, \cdots , P_n$ এর ক্রম (sequence) দেখে লেখা যাক

$P_{n+1}= f(P_n)$

একেই বলে পোঁয়াকারে ম্যাপ। পোঁয়াকারে বললেন যে আমি যদি সাধারণ সূত্রের সাহায্যে $f(x)$ -এর চেহারা বার করতে পারি তাহলে ঐ ক্রম $P_1, P_2, \cdots , P_n$ -এর বিশেষত্বও বুঝতে পারবো। ব্যাপারটাকে আরও সহজ করার জন্য আমি কেবলমাত্র ধনাত্মক $X$ -অক্ষের অংশটাই দেখতে পারি অর্থাৎ চিত্র ৩-এ দেখব কেবল $P_1, P_3, P_5, P_7, \cdots$ বিন্দুগুলি। যদি কোন কক্ষপথ সীমাহীন ভাবে বেড়ে যায় তাহলে তার ব্যাপারে আমাদের কোন মাথাব্যথা নেই। আমরা কেবল মাত্র সেইসব কক্ষপথ নিয়ে চিন্তিত যাদের মূলবিন্দু থেকে একটি সর্বাধিক দূরত্ব $N$ রয়েছে এবং সেক্ষেত্রে আমরা $P_n$ -এর পরিবর্তে ব্যবহার করবো একটা নতুন চলরাশি (variable):

$X_n= \frac{P_n}{N}$

এর মান কখনো এক-এর বেশি হতে পারেনা, অর্থাৎ $0 \leq X_n \leq 1$ । আমাদের আলোচ্য বিষয় তাহলে হবে:

$X_{n+1}= f(X_n)$ [ $0 \leq X_n \leq 1$ ], যেকোনো $n$ -এর জন্য।

এইবার আমরা আলোচনাটাকে আরেকটু ফোকাস করতে $f(x)$ -এর একটা বিশেষ চেহারা ধরে নেবো (এর সাথে পৃথিবীর কক্ষপথের সম্পর্ক অনেকটাই কাল্পনিক):

$f(x)= rX(1-X)$

উপরোক্ত সমীকরণে $r$ একটি পূর্বনির্ধারিত সংখ্যা। যেহেতু $f(x) \leq 1$ এবং $X(1-X)$ -এর সর্বোচ্চ মান $\frac{1}{4}$ , $r$ সংখ্যাটির সবচেয়ে বেশি মান হতে পারে $4$ । আমরা যে ম্যাপটাকে বিশ্লেষণ করবো তাকে বলা হয় লজিস্টিক ম্যাপ (logistic map)। এবং এটিকে আমরা লিখবো এইভাবে:

$X_{n+1}= f(X_n)= rX_n(1-X_n)$

ফিক্সড পয়েন্ট বা স্থির বিন্দু

আমরা প্রথম ছবিটিতে দেখেছিলাম, পৃথিবীর কক্ষপথ এমন যে $X_n$ -এর মানের কোনো পরিবর্তন হচ্ছে না। বারবার পৃথিবী $X$ -অক্ষ পার হচ্ছে একই $X$ -এ। প্রথমেই তাহলে এই প্রশ্নটা স্বাভাবিক: কোন ক্ষেত্রে $f(X_n)= X_n$ । এইধরণের $X_n$ -কে বলা হয় ফিক্সড পয়েন্ট (fixed point)। একে নির্ণয় করা হয়

$X^*= f(X^*)$

এই সমীকরণটির সাহায্যে। লজিস্টিক ম্যাপ-এর ক্ষেত্রে $f(X^*)= rX^*(1-X^*)$ এই সমীকরণটার দুটো সমাধান আছে। অর্থাৎ ম্যাপটার দুটো ফিক্সড পয়েন্ট আছে:

$X^*= 0$ , $X^*= 1 - \frac{1}{r}$

এইবার প্রথম ছবিটা দেখা যাক। পৃথিবীর সূর্য প্রদক্ষিণের কক্ষপথ বারবার $X$ -অক্ষকে একই বিন্দুতে ছেদ করছে। অতএব কক্ষপথটি পোঁয়াকারে ম্যাপ (Poincare map)-এর একটি ফিক্সড পয়েন্ট। যেহেতু প্রদক্ষিণের সময় ছেদের মান $X^*$ শূন্য নয়, তাই পৃথিবীর কক্ষপথের সঠিক ফিক্সড পয়েন্ট হবে:

$X^*= 1- \frac{1}{r}$

ফিক্সড পয়েন্ট থাকাই কিন্তু যথেষ্ট নয়। গতি শুরু হওয়ার সাথে সাথেই তো কেউ ফিক্সড পয়েন্ট-এ বসে থাকবে না। সময়ের সাথে ফিক্সড পয়েন্ট-এ পৌঁছবে। অতএব প্রশ্ন হলো: কোথাও একটা শুরু করিয়ে দিলে ফিক্সড পয়েন্ট-এ পৌঁছে যাবে কি?

এর উত্তর পাওয়ার জন্য দেখা হয় ফিক্সড পয়েন্ট কাছাকাছি $X^*$ -এর কাছাকাছি পৌঁছলে ঠিক কি হবে। যদি হয় $X_n= X^* + \delta X_n$ যেখানে $\delta X_n$ খুব ছোট, তাহলে যে $X_{n+1}= X^* + \delta X_{n+1}$ পাওয়া যাবে, সেখানে $|\delta X_{n+1}|$ কি $|\delta X_n|$ -এর চেয়ে ছোট হবে? যদি না হয়, তাহলে তো কোনোদিনই $X^*$ -এ পৌঁছবে না। $X^*$ -এ পৌঁছোবার প্রথম শর্ত অর্থাৎ $|\delta X_{n+1}| < |\delta X_n|$ , এটা মানলে ফিক্সড পয়েন্ট-টাকে স্টেবল ফিক্সড পয়েন্ট (stable fixed point) বলে।

আগের সমীকরণগুলোর সাহায্যে লেখা যায়:

$X_{n+1}= f(X_n)= f(X^* + \delta X_n)= f(X^*) + \delta X_n \frac{df}{dX}|_{X^*} + \cdots$

ওপরের টেলর এক্সপ্যানশন (Taylor expansion)-এ $(\delta X_n)^2$ ইত্যাদি পরের টার্মগুলো খুব ছোট বলে ছেড়ে দেওয়া হলো। অতএব, যাকে $\delta X_{n+1}$ বলছি, সেটা হলো

$\delta X_{n+1}= \delta X_n \frac{df}{dX}|_{X^*}$

এবং স্টেবল ফিক্সড পয়েন্ট –এর জন্য চাই:

$\frac{df}{dX}|_{X^*} < 1$

এইবার দেখা যাক $X^*= 1- \frac{1}{r}$ স্টেবল কিনা। $X^*$ -এর মান বসালে দেখা যায়:

$\frac{df}{dX}|_{X^*}= r(1-2X^*)= 2-r$

স্টেবিলিটির জন্য চাই $|2-r| < 1$ অর্থাৎ $1<r<3$ । অতএব লজিস্টিক ম্যাপকে যদি পৃথিবীর কক্ষ পথে সঠিক ম্যাপ হতে হয় তাহলে $r$ -এর মান $1$ এবং $3$ -এর মধ্যে থাকতে হবে।

একাধিক ফিক্সড পয়েন্ট-এর মধ্যে চরকিপাক

চিত্র ২-তে যে কক্ষপথটি দেখলাম, সেটি কি লজিস্টিক ম্যাপ-এর সাহায্যে পেতে পারব? এই কক্ষপথের বিশেষত্ব দুটি বিন্দু ( $P_1$ এবং $P_3$ ) যাদের $X$ -অক্ষের সাথে ছেদ $X_1^*$ এবং $X_2^*$ , তারা এই ক্রমে আসবে $X_1^*, X_2^*, X_1^*, X_2^*, \cdots$ । অর্থাৎ এই $P_1, P_3, P_1, P_3, \cdots$ দুটো বিন্দুর মধ্যে কণাটি ঘুরপাক খাবে।

গতিপথ $f(x)$ -এর কথা ভাবলে:

$X^*_2= f(X^*_1)$ এবং $X^*_1= f(X^*_2)$

এর থেকে সহজেই দেখতে পাই:

$X^*_1= f(X^*_2 )=f(f(X^*_1))$ এবং $X^*_2= f(X^*_1 )=f(f(X^*_2))$

অতএব $X^*_1, X^*_2$ বিন্দু দুটি $f(f(X))$ অপেক্ষকটির ফিক্সড পয়েন্ট।

লজিস্টিক ম্যাপের জন্য $f(X)= rX(1-X)$ , তাই

$f(f(X))= rf(1-f)=r^2 X(1-X)[1-rX(1-X)]$

এই অপেক্ষকটির ফিক্সড পয়েন্ট $X^*$ নির্ণয় করতে হ’লে আমাকে সমাধান করতে হবে:

$X^*=r^2 X^* (1-X^* )[1-rX^* (1-X^*)]$

পরিষ্কার দেখা যাচ্ছে উপরোক্ত দ্বিঘাত সমীকরণের দুটি সমাধান $X^* = 0$ এবং $1- \frac{1}{r}$ । অন্য দুটি সমাধান হচ্ছে যে $X^*_1$ এবং $X^*_2$ আমাদের প্রয়োজন। এই $X^*_1, X^*_2$ আমাদের চিত্র ২ এর $P_1, P_3$ বিন্দু দুটি। এই সনাক্তকরণ সম্পূর্ণ সঠিক হওয়ার জন্য $X^*_1, X^*_2$ কে স্টেবল ফিক্সড পয়েন্ট হতে হবে – নিজেদের হাত পাকানোর জন্য প্রমাণ করে নেবে যে $X^*_1, X^*_2$ স্টেবল যদি এইটা ঠিক হয়:

$3<r< \sqrt 6+1$

শুরুর অল্প তফাৎ যখন চটজলদি বেড়ে যায়

এইবার আমরা দেখতে চাই লজিস্টিক ম্যাপ কি কখনো এমন একটি কক্ষপথ $X_1, X_2, X_3, \cdots, X_n$ দিতে পারে যেখানে ওই প্রাথমিক পরিস্থিতি-র উপর অতিনির্ভরশীলতা (sensitivity to initial conditions) দেখা যাবে। সুবিধের জন্য আমরা $r=4$ ধরে নিই। অর্থাৎ:

$X_{n+1}= 4x_n(1-x_n)$

একটা রূপান্তর (transformation) করা যাক:

$X_n= \sin^2{\theta_{n}}$ , $0 \leq \theta \leq \frac{\pi}{2}$

রূপান্তরটা করলে দাঁড়ায়:

$\sin^2{\theta_{n+1}}= 4\sin^2\theta_n \cos^2\theta_n= \sin^2 2\theta_n$

যার থেকে পাই
$\theta_{n+1}= 2\theta_n, 0 \leq \theta_n \leq \frac{\pi}{4}$ ,
$\theta_{n+1}= \pi - 2\theta_n, \frac{\pi}{4} \leq \theta_n \leq \frac{\pi}{2}$

যদি বলি $Y_n= \frac{2}{\pi}\theta_n$ , তাহলে: $0 \leq Y_n \leq 1$ ,

এবং

$Y_{n+1}= 2Y_n, 0 \leq Y_n \leq \frac{1}{2}$ ,

$Y_{n+1}= 2(1-Y_n), \frac{1}{2} \leq Y_n \leq 1$

এই ম্যাপটি যাকে আমরা লিখব:

$Y_{n+1}= g(Y_n)$

একে বলা হয় টেন্ট ম্যাপ (tent map) কারণ এর গ্রাফ হচ্ছে এইরকম তাঁবুর মতো:

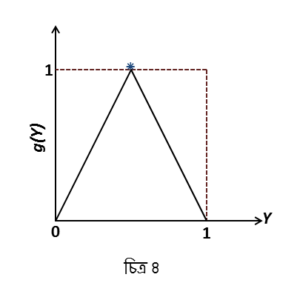
এবার প্রশ্ন, আমি যদি $Y=Y_0$ দিয়ে শুরু করি তাহলে $N$ -খানা ধাপের পরে কোথায় পৌঁছব? প্রথম ধাপে:

$Y_1= g(Y_0)$

তারপর $Y_2= g(Y_1)= g(g(Y_0))$

তারপর $Y_3= g(Y_2)= g(g(g(Y_0)))$

তারপর $Y_n= g(g(\cdots g(Y_0) \cdots))$

উত্তরটা জানতে হলে আঁকতে হবে $g(g(Y)), g(g(g(Y)))$ ইত্যাদি-র গ্রাফগুলোকে। একটু ভাবলেই দেখবে ছবিগুলো হচ্ছে এইরকম (আমরা $g(g(Y))$ -কে লিখবো $g^2(Y)$ , $g(g(g(Y)))$ -কে লিখবো : $g^3(Y)$ )

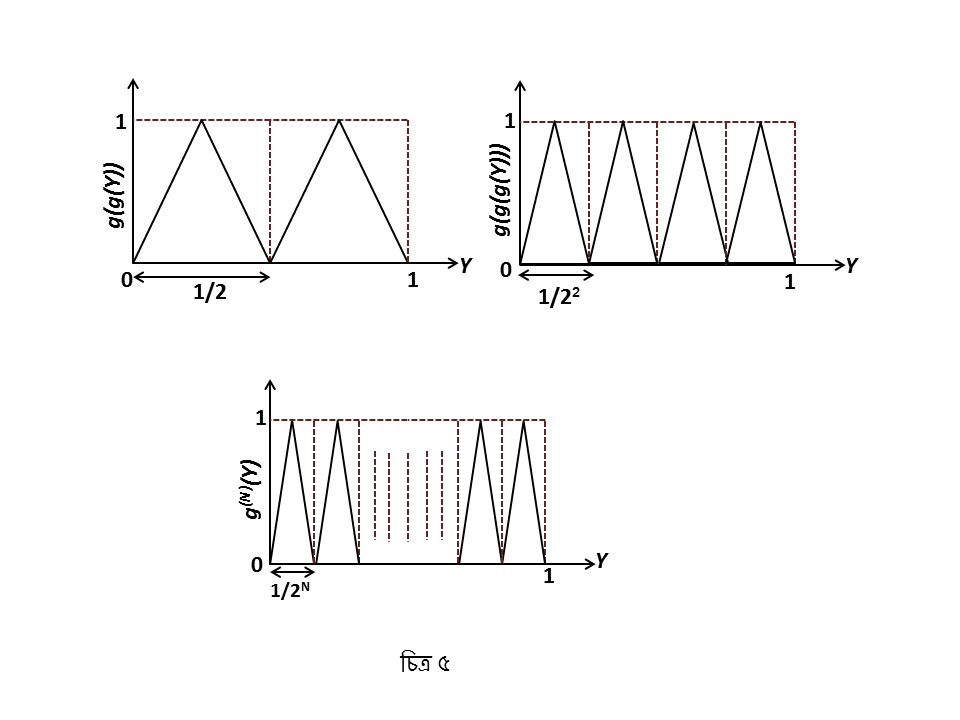
উপরের ছবিগুলোর সাহায্যে দেখা যাচ্ছে

$Y_0$ যদি হয় $\frac{1}{8}$ , তাহলে $Y_1= \frac{1}{4}, Y_2= \frac{1}{2}, Y_3= 1$

যদি $Y_0$ হয় $\frac{1}{16}$ , তাহলে $Y_1= \frac {1}{8}, Y_2= \frac{1}{4}, Y_3= \frac{1}{2}, Y_4= 1$

অতএব কণাটির অবস্থার বিবর্তন যদি হয় $Y_{n+1}= g(Y_n)$ অনুযায়ী, তাহলে $Y_0= \frac{1}{8}$ হলে তিনধাপ পরে $Y_3= 1$ । কণাটি $Y'_0= \frac{1}{16}$ −এ থাকলে, তিন ধাপ পরে সে থাকবে $Y'_3= \frac{1}{2}$ -এ। তার মানে শুরুতে যদি মাপজোখের ফলে কণাটির অবস্থার তফাৎ হয় $\delta Y_0= Y'_0 - Y_0= \frac{1}{16}$ , তিনধাপ পরে সেটা দাঁড়িয়েছে $\delta Y_3= Y'_3-Y_3= \frac{1}{2}$ ।

ধরা যাক, শুরুর তফাৎ-টা আরো ছোট:

$Y_0= \frac{1}{8}+\frac{1}{2^{10}}$

$Y'_0= \frac{1}{8}+\frac{1}{2^{11}}$

তাহলে দশটা ধাপ পরে $Y_{10}$ হবে $1$ আর হবে $0.5$ । প্রথমে তফাৎ ছিল $Y_0-Y'_0= 0.00048 \cdots$ আর দশ ধাপ পরে সেটা দাঁড়িয়েছে $0.5$ ! তার মানে দুটো প্রাথমিক অবস্থার তফাৎ যেখানে ছিল $2^{-11}$ , দশ ধাপ পর তাদের তফাৎ অর্থাৎ 1024 গুন বেড়েছে। এই ধরণের অকল্পনীয় চলনকে ‘প্রাথমিক অবস্থার উপর অতিনির্ভরশীল’ বলা হয়। এই অতিনির্ভরশীলতার একটা মাপকাঠি আছে যাকে বলে লিয়াপুনভ ইনডেক্স (Lyapunov index)। দুটি প্রাথমিক অবস্থার তফাৎ $t= 0$ -তে অর্থাৎ একদম শুরুতে যদি $d_0$ হয় আর $N$ -খানা ধাপের পরে হয় $d_N$ , তাহলে এইভাবে লিয়াপুনভ ইনডেক্স $\lambda$ বার করা যায়:

$\lambda= \displaystyle \lim_{\substack{N\to\infty \\ d_0\to0}}\frac{1}{N}\ln (\frac{d_N}{d_0})$

এই লিয়াপুনভ ইনডেক্স যদি ধনাত্মক হয়, তাহলে কণাটির চলন প্রাথমিক অবস্থার উপর অতিনির্ভরশীল বা কেওটিক (chaotic) হবে। যে বিষয়ে এই ধরণের কেওটিক চলন অন্তর্ভুক্ত তাকে কেয়স (chaos) বলে। আমরা যে টেন্ট ম্যাপটি দেখলাম, তার জন্য যদি $d_0$ হয়

$d_0= \frac{1}{2^{N+1}}$

তাহলে $d_N$ হবে $\frac{1}{2}$ । সেক্ষেত্রে লিয়াপুনভ ইনডেক্স হবে $\lambda= ln(2) > 0$ । তাই টেন্ট ম্যাপ থেকে যে চলন পাওয়া যায়, সেটা কেওটিক।

এইবার ফিরে আসা যাক আবহাওয়ার পূর্বাভাস সম্বন্ধে। হাওয়ার গতিবেগের জন্য নিউটনের সূত্র লিখলে তার থেকে যে পোঁয়াকারে ম্যাপ বেরোবে, সেটা আমাদের টেন্ট ম্যাপ-এর মতন সহজ না হলেও, টেন্ট ম্যাপের যে বিশেষত্ব আসে, বায়ুমণ্ডলেও প্রায়শঃই সেই বিশেষত্ব থাকে। আবহাওয়া সম্বন্ধে সঠিক পূর্বাভাসের জন্যে প্রথমেই প্রয়োজন চারদিকের বায়ুর গতিবেগ ও বায়ুচাপ সম্বন্ধে প্রায় নির্ভুল জ্ঞান এবং দ্বিতীয়ত প্রয়োজন উচ্চমানের গণনার সুব্যবস্থা। এই দুটি হলে পরেও কেওটিক চলনের ফলে পূর্বাভাসে ভুলভ্রান্তি হতে পারে। আজ থেকে পঞ্চাশ বছর আগে আমাদের দেশে কেন হয়তো গোটা পৃথিবীতেই ভালো বায়ুমণ্ডল-সংক্রান্ত তথ্য জোগাড় করা অত্যন্ত কঠিন ছিল। আজকে উচ্চমানের কৃত্রিম উপগ্রহের কল্যাণে এ ব্যাপারে ততটা সমস্যা নেই, সুপারকম্পিউটারও সর্বত্র। তাই আজকের আওহাওয়াবিদদের জীবন অনেক সহজ। কিন্তু তবুও দেখবে কালকের আবহাওয়ার পূর্বাভাস যতটা বিশ্বাসযোগ্য, দুই তিন দিনের বেশি হয়ে গেলে ততটা নয়। সেখানে এখনো কেওটিক চলনের অনিশ্চয়তা তার ছাপ রেখে যায়।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.