রঙসংখ্যার খোঁজ - একটি অবিচ্ছিন্ন ট্রেইলিং পথ ধ'রে …

শঙ্কর বসু

(Asutosh College)

 

17 Apr 2020

Link: https://bigyan.org.in/trailing-the-chromatic-numbers

কম্বিনেটোরিয়াল অপ্টিমাইজেশন এবং গ্রাফ তত্ত্বের এক দূরতিক্রম সমস্যা ‘গ্রাফকে রঙ করার সমস্যা’র সমাধানের সন্ধান।

হিসেব-নিকেষের উপক্রমণিকা

ছোটবেলায় বড়দের কাছে একটা ধাঁধা আমরা সবাই শুনেছি । সে এক হৈদর মাঝি, হাট থেকে একটা আস্ত বাঘ, একটা নধর ছাগল আর এক মস্ত আঁটি ঘাস কিনেছে । ধরে নেওয়া যাক, মগনলাল মেঘরাজের মতো সেও এক ‘প্রাইভেট সার্কাস’ খুলতে চায় । তো, এখন তাদের নিয়ে সে তার ছোট্ট আদরের নৌকোটিতে দেবে মারের সাগর পাড়ি । অথচ, “ঠাঁই নাই ঠাঁই নাই ছোটো সে তরী … ” । আর সেই স্থানসংকুলানগত কারণেই প্রত্যেকবার তিনটির যেকোনো একটিকেই সে নৌকোয় তুলতে পারে । দুটিকে পারেনা । তা, এখন কি পারম্পর্য্যে তাদের একাধিক্রমে সঙ্গে নিলে বাঘ ছাগল’কে একা পাবেনা, আর, ‘কি-না-খায়’ ছাগলেরও মওকা মিলবেনা একা পেয়ে ঘাসের আঁটিটি কচকচ ক’রে চিবুনোর । 

একটা ক্রম বা একটা উত্তর এরকম হতে পারে । 

(১) প্রথমে ছাগল নিয়ে ওপারে যাওয়া, এপারে, বাঘের ঘাসে অরুচি । 

(২) খালি নৌকো নিয়ে ফেরত এসে, তারপর, বাঘকে তুলে নিয়ে পাড়ি জমানো । ওপারে বাঘ রেখে, নৌকোয় ছাগল তুলে নিয়ে দ্বিতীয়বার ফেরত আসা ।

(৩) অতঃপর, এপারে ছাগল রেখে, ঘাসের আঁটি তুলে নিয়ে ওপারে রেখে আসা (ফলত এখন ওপারে, বাঘের ঘাসে অরুচি) ।

(৪) খালি নৌকো নিয়ে ফেরত এসে এবার ‘শেষ পারানির কড়ি’ ছাগল নিয়ে শেষবারের মতো পাড়ি জমানো । 

এভাবে নিয়ে গেলে সবদিক রক্ষা পায় । আবার এই ক্রমের (sequence) উনিশ-বিশ অদল-বদল ক’রে নিয়ে বিকল্প ক্রমও থাকতে পারে । থাকতে পারে বিকল্প সমাধান । গণিত ও অ্যালগরিদমে ‘কম্বিনেটোরিক্স’ (Combinatorics) শাখাভুক্ত এই ধরণের সমস্যাকে বলা হয় – কম্বিনেটোরিয়াল অপ্টিমাইজেশান (ছোটো ক’রে, CO) । অর্থাৎ নানান সম্ভাবনার মধ্যে থেকে উপযুক্ত সমবায়টি (combination) খুঁজে বের করতে হবে, যাতে প্রদত্ত সমস্যাটির একটি যথাযোগ্য উত্তম সমাধান (optimized solution) মেলে । কিন্তু, সেই সমাধানটিই যে নির্ভুল ভাবে সর্বোত্তম সমাধান (best solution) হবে, তা হলফ ক’রে বলা যাবে না । উড়িয়ে দেওয়া যাবেনা  বিকল্প সমাধানের সম্ভাবনার কথা । তার যথার্থ কারণ হ’ল এই যে, এই জাতের সমস্যার কোনও সর্বগ্রাহ্য বিশ্লেষণাত্মক (analytical) সমাধান হয়না ।

যেকোনো ধরনের বহুমাত্রিক সংযোগে  কে কার সঙ্গে সম্পর্কিত (অর্থাৎ যুক্ত) জানলেই তাদেরকে “গ্রাফ” হিসেবে উপস্থাপন করা যায়।

অর্থাৎ, খাতা কলমে, ফর্মুলায় ফেলে, ক’ষে বের করা যায়না এদের উত্তর । পারিভাষিক ভাবে বলতে গেলে, এই জাতের সমস্যাগুলিকে সাধারণ সমীকরণভুক্ত করা যায়না(i.e., without having a  general solution) । বরং, সমস্যাগুলি ভীষণ রকম প্রসঙ্গ-নির্ভর (context dependent) । ফলত, কোনও একটি বিশেষ উদাহরণের ক্ষেত্রে উত্তর মিলিয়ে দ্যাখবার উপায় নেই । উত্তরের ঠিক-ভুলের বিচার পারতপক্ষেই নির্ভর করছে একধরণের যুক্তিনিষ্ঠ কল্পনা-প্রতিভার (বা সহজাত বুদ্ধির) ওপর – সাহেবরা যাকে তারিফ ক’রে পেয়ারের নামে ডাকেন –  “ইণ্টুইশন (Intuition)” !

গ্রাফ তত্ত্বের গোড়ার কথা

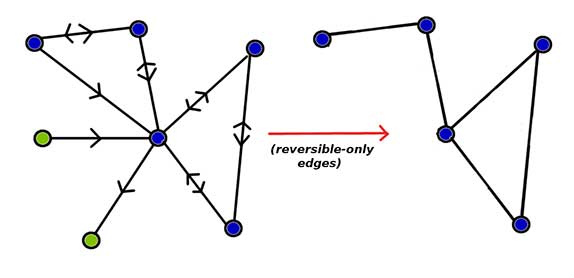
গ্রাফকে রঙ করার সমস্যা (the ‘Graph Coloring Problem’) এই জাতের একটি প্রায় ২০০ বছরের পুরোনো সমস্যা । যেখানে, “গ্রাফ” হ’ল চলিত কথায় নেটওয়ার্ক বা বহুমাত্রিক সংযোগের এক জাল-সদৃশ বিমূূর্ত চিত্রায়ণ (an abstract representation of contextual interconnections) ! এই জালের সংযোগবিন্দুগুলিকে বলে “নোড (Node)” বা “শীর্ষ” (vertex) আর তাদের মধ্যের আকর সুতলিগুলিকে বলা হয় “এজ (edge)” বা “বাহু” (link) ! যেকোনো ধরনের বহুমাত্রিক সংযোগ তা সে বন্ধুত্বের হোক বা শত্রুতার, অন্তর্দেশীয় হোক বা জীবকোষের ভেতর প্রোটিনের − শুধুমাত্র কে কার সঙ্গে সম্পর্কিত (অর্থাৎ যুক্ত) জানলেই তাদেরকে “গ্রাফ” হিসেবে উপস্থাপন করা যায় । এই যোগাযোগ আবার নির্দিষ্ট অভিমুখ যুক্ত  (directed graphs) অথবা নির্দিষ্ট অভিমুখহীন (undirected) – দুই’ই হতে পারে ।   প্রথম ধরণের গ্রাফের ক্ষেত্রে (for directed graphs) বাহুগুলির একেকটি নির্দিষ্ট অভিমুখ থাকে, কেননা সংজ্ঞানুসারে তারা স্বভাবত যেকোনো একতরফের যোগাযোগকেই (ক থেকে খ; অথবা, খ থেকে ক) বোঝায় । ধরা যাক, দেশের বিভিন্ন বিমানবন্দরের মধ্যে বিমান যাতায়াতের নেটওয়ার্ক । এখন কোলকাতা (ক) থেকে বাগডোগরার (খ) সরাসরি বিমান থাকলেও উল্টোটা নেই । আবার কোলকাতা ও মুম্বাইয়ের (গ) মধ্যে সরাসরি বিমানের যাতায়াত দুদিকেই । এইধরনের উভয়-সম্ভাবনায় (একতরফা বা দ্বিমুখী) সম্মৃদ্ধ সংযোগের সংগ্রহকে গ্রাফ হিসেবে দেখাতে গেলে সেখানে এই দুধরনের বাহুকে যথাক্রমে একমুখী তীরচিহ্ন (ক→খ) ও উভমুখী তীরচিহ্ন (ক↔গ) দিয়ে আঁকা হয়ে থাকে । দ্বিতীয় প্রকার গ্রাফের ক্ষেত্রে (for undirected graphs) আগের উদাহরণটির সাথে সাযুজ্য রেখে আমরা আগের নেটওয়ার্কটির সেইসমস্ত বাহুগুলিকে ছেঁকে নিতে পারি, যারা উভয়দিকেই সরাসরি বিমানের যাতায়াতকে নির্দেশ করে । অর্থাৎ এইধরনের গ্রাফের সমস্ত বাহুই কার্যত দ্বিমুখী বা উভমুখী । এভাবে ছেঁকে নেওয়া দ্বিমুখী বাহুগুলির সম্মিলিত সংগ্রহ (the collective ensemble of reversible edges) একটি অভিমুখহীন (undirected) গ্রাফের জন্ম দেবে । এবং এক্ষেত্রে, অভিমুখের প্রশ্ন অপ্রাসঙ্গিক হয়ে পড়ায় বাহুগুলিকে আঁকা হয় অনুভূমিক দাঁড়িচিহ্ন (—) বা সোজা কথায়, ‘ড্যাশ’ দিয়ে ।

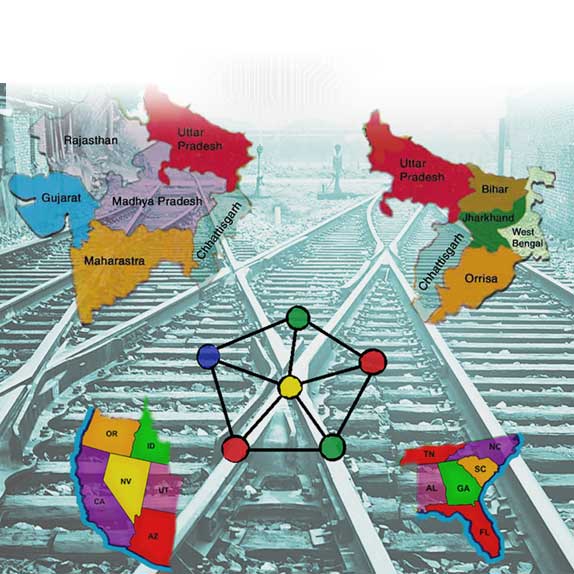
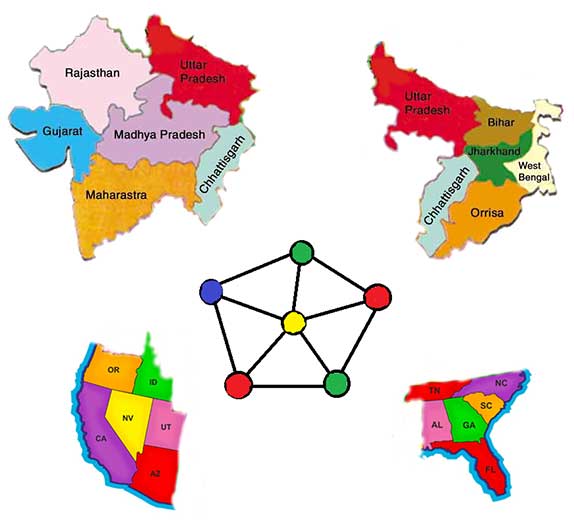
১৮৫২ সালে ইংলিশম্যান ফ্রান্সিস গাথ্রি সাহেব মহান ব্রিটেনের কাউণ্টিগুলির “ম্যাপ” (অর্থাৎ মানচিত্র) বানাতে গিয়ে দেখলেন যে পাশাপাশি কাউণ্টিগুলির রঙ আলাদা না রাখলে চোখের এক-দেখায় তাদের চট্ ক’রে আলাদা ক’রে চেনা যায়না । চিন্তাশীল গাথ্রি সাহেব ভাবতে বসলেন, তা যদি হয়, তবে রঙের অপচয় না ক’রে ন্যূনতম কতগুলি রঙ দিয়ে এই ম্যাপ আঁকা সম্ভব ! এই অন্বেষণ জন্ম দিল ম্যাপ’কে রঙ করার সমস্যার (Map coloring problem) । বিস্তৃত বৈচিত্রে সম্মৃদ্ধ নানা জাতের ম্যাপ’কে এভাবে রঙ করতে গিয়ে গাথ্রি সাহেব দেখলেন যে ম্যাপ যেমনই হোক, চারটের বেশী রঙ কোথাও লাগছেনা । এভাবে বহু বহু ম্যাপ পরীক্ষা করার পরেও যখন এই ফলাফলের কোনো ব্যত্যয় হলনা, তখন গাথ্রি সাহেব পেশ করলেন তাঁর বিখ্যাত চার রঙের স্বতঃসিদ্ধ (four color conjecture) ।

চারটি ভূভাগের যে কোনও একটি থেকে শুরু করে প্রতিটি সেতু কেবলমাত্র একবার পেরিয়ে এবং বাকি তিনটি অঞ্চলের প্রতিটিকে ঠিক একবার ক’রে ছুঁয়ে আবার শুরুর জায়গায় ফিরতে হবে।

যার মূল প্রস্তাবনাটি হল এই যে যেকোনো দেশের (বা মহাদেশের বা পৃথিবীর – যা খুশি) মানচিত্রকে (অর্থাৎ তার অঙ্গরাজ্য বা দেশ বা মহাদেশগুলিকে) রঙ করার ক্ষেত্রে চারটি রঙই যথেষ্ট, যাতে করে কোনও দুটি সংলগ্ন (adjacent) বা পড়শি (neighboring) অঞ্চল (রাজ্য / দেশ / মহাদেশ – যেখানে যেমন) একই রঙে রঞ্জিত না হয় । অর্থাৎ এক দেখায় চট্ করে তাদের স্বতন্ত্র বলে চিনে নেওয়া যায় । যদিও ১২৫ বছরেরও বেশি সময় লেগেছিল স্বতঃসিদ্ধটিকে উপপাদ্য হিসেবে প্রতিষ্ঠিত করতে, অর্থাৎ স্বতঃসিদ্ধটির বিধিবৎ প্রমাণ (formal proof) খুঁজে বের করতে (১৯৭৭, কেনেথ অ্যাপেল, উলফ হ্যাকেন ) ।

কনিংসবার্গের সাতসেতুর সমস্যা

এরও এক শতাব্দী আগে, ১৭৩৬ সালে, এক সুইস গণিতজ্ঞ, লিওনার্ড অয়েলার কিংবদন্তী ‘কনিংসবার্গের সাতসেতুর সমস্যা’র (Konigsberg’s seven bridge problem) সমাধান করতে গিয়ে বিধিবদ্ধ ভাবে ‘গ্রাফ থিওরি’ শাখাটির প্রথাগত চর্চার জন্ম দেন । রাশিয়ার তৎকালীন প্রুশিয়া (বর্তমানে কালিনিনগ্রাদ) অঞ্চলে কনিংসবার্গ শহর ছিল প্রেজেল নদীর দুইপার জুড়ে এবং নদীর মাঝে নেইপহফ ও লোমসে নামের দুটি বড় দ্বীপ নিয়ে । শহরটির এই চারটি বিচ্ছিন্ন ভূখণ্ড ছিল মোট সাতটি সেতুর দ্বারা সংযুক্ত । এবং এই ‘সাতসেতুর সমস্যা’টি হল ওই চারটি ভূভাগের যে কোনও একটি থেকে শুরু করে প্রতিটি সেতু কেবলমাত্র একবার পেরিয়ে এবং বাকি তিনটি অঞ্চলের প্রতিটিকে ঠিক একবার ক’রে ছুঁয়ে আবার শুরুর জায়গায় ফিরে আসার সম্ভাব্য পথ খুঁজে বের করার সমস্যা ।

সমস্যাটির সমাধান করতে গিয়ে অয়েলার সাহেব প্রথম কনিংসবার্গের ম্যাপ’কে গ্রাফের বিমূর্ত প্রতিচিত্র হিসেবে উপস্থাপন করলেন – যেখানে পূর্বোক্ত প্রতিটি বিচ্ছিন্ন ভূখণ্ড হল একেকটি শীর্ষ এবং তাদের মাঝে সংযোগকারী সেতুগুলি হল বাহু । গ্রাফ থিওরি কাজে লাগিয়ে অয়েলার প্রমাণ করলেন যে ‘কনিংসবার্গের সাতসেতুর সমস্যা’র আদতেই কোনও সমাধান নেই ।

– সংখ্যক শীর্ষ, – সংখ্যক বাহু এবং – সংখ্যক পৃষ্ট (face) বিশিষ্ট সামতলিক গ্রাফের ক্ষেত্রে

অর্থাৎ এমন কোনো পথ’ই নেই (বা থাকতে পারেনা) যা ধ’রে চলতে থাকলে সমস্যাটির (পূর্বোক্ত) শর্তদুটি নির্ভুল ভাবে মেনে আবার শুরুর বিন্দুতে ফিরে আসা সম্ভব । এই কারণেই এটি একটি কিংবদন্তী ব্যাসকূট (paradox) হয়ে রয়েছে সেই থেকে ! এই সাতসেতুর সমস্যা নিয়ে ঘাঁটতে ঘাঁটতে অয়েলার সাহেব গ্রাফ থিওরির একটি প্রারম্ভিক পারিভাষিক শব্দকোষও বানিয়ে ফেললেন; যাতে ‘ম্যাপ’ বলতে বোঝায় বস্তুত সামতলিক গ্রাফ (planar graph) – যে গ্রাফের শীর্ষগুলি হ’ল ম্যাপটির সীমায় ঘেরা একেকটি ভৌগলিক অঞ্চল আর এরকম দুটি অঞ্চলের মধ্যে কাঁটাতারের সীমানা (border) থাকলে ওই শীর্ষদুটি সংযুক্ত হল বাহু’র দ্বারা । অধিকন্তু, এ হেন একটি সামতলিক গ্রাফের মধ্যে কোনো বিচ্ছিন্ন উপাংশ (disjoint component) না থাকলে তাদের বলা হল সংযুক্ত সামতলিক গ্রাফ (connected planar graph) । অয়েলার এও দেখালেন যে কোনও সংযুক্ত সামতলিক গ্রাফের (বা ম্যাপের) যদি  – সংখ্যক শীর্ষ, – সংখ্যক বাহু এবং – সংখ্যক পৃষ্ট (face) থাকে তবে, হয় । আর, এভাবেই, “ম্যাপ রঙ করার সমস্যা” থেকে আরো সাধারণ সমস্যা হিসেবে  উঠে এল “গ্রাফ রঙ করার সমস্যা” । কিম্বা, ঘুরিয়ে বললে, “ম্যাপ রঙ করার সমস্যা” আদতে এক বিশেষ শ্রেণীর গ্রাফকে (সামতলিক গ্রাফ) রঙ করার সমস্যা বই নয় ।

অন্যরকম গ্রাফ রঙ করার সমস্যা

এর বিপ্রতীপে, এক অন্য শ্রেণীর গ্রাফ’ও থেকে যায় যাদের ক্ষেত্রে অয়েলারের পূর্বোক্ত সূত্রটি খাটেনা, যাদের খাতার পাতায় আঁকতে গেলে নিদেনপক্ষে একজোড়া বাহু (edge) অবধারিত ভাবে পরষ্পরছেদী (intersecting) হয়ে পড়বে, ফলত, তারা আপাদমাস্তক আর ওই খাতার পাতার সমতলে থাকবে না – এরাই অসামতলিক (non-planar) গ্রাফ !

আমাদের মূল আলোচনা এই ‘গ্রাফ রঙ করার সমস্যা’টি নিয়েই । সমস্যাটির একেবারে হৃদকেন্দ্রে রয়েছে রঙসংখ্যা বা ক্রোম্যাটিক নাম্বারের খোঁজ – যা কিনা সেই ন্যূনতম সংখ্যা, যতগুলি রঙ দিয়ে একটি গ্রাফের শীর্ষগুলিকে চিহ্নিত (level) করা চলে, যাতে ক’রে কখনোই কোনও দুটি সংযুক্ত শীর্ষ একই রঙ না পায় (no two adjacent nodes share the same color) ! আবারো স্মরণ করা ভালো যে, এই জাতের সমস্যার কোনও বিশ্লেষণাত্মক সমাধান হয়না – এরা ভীষণ রকম প্রসঙ্গ নির্ভর ! ফলত সেক্ষেত্রে প্রয়োজন একটি দূরদর্শী সবজান্তা সিধুজ্যাঠাচিত মাস্টার প্ল্যানের অর্থাৎ অ্যালগরিদমের । এবং তাকে বাস্তবায়িত করতে দরকার উন্নত কম্পিউটার ও কোডিং স্কিল ! অর্থাৎ সোজা বাংলায় যাকে বলি, গণনা ! গণনা মানেই আবার সময়ের প্রশ্ন বা অন্য কথায় গণনাত্মক জটিলতার (computational complexity) প্রশ্ন ! যে গণনা যত জটিল, তার সমাধান তত সময়-সাপেক্ষ !

গণনার শ্রেণীবিভাগ

জটিলতার দৃষ্টিকোণ থেকে গণনার এই জটিলতা অনুযায়ী কোনো গণনাত্মক সমস্যাকে দুভাগে ভাগ করা যায়-

১) বহুঘাতে নির্নেয় (deterministic in polynomial time: )

২) বহুঘাতেও অনির্নেয় (Non deterministic in polynomial time: ) ।

মার্কিন বিজ্ঞানী রিচার্ড কার্প ১৯৭২ সালে তৈরী করেন তাঁর বিখ্যাত আগাগোড়া সমস্যার তালিকা।

কোনো গণনাত্মক সমস্যার জটিলতা (ধরা যাক, ) যদি  সমস্যাটির  ইনপুট আকারের দ্বিঘাত, ত্রিঘাত বা কোনো উচ্চতর বহুঘাতের অপেক্ষক (function: : যেখানে হল ঘাত) হিসেবে বাড়ে তবে তাকে বহুঘাতে নির্ণেয় বলা হয় । এভাবে নির্ণীত ঘাতটি ভগ্নাংশ (fractional exponent) হলেও ক্ষতি নেই । অন্যথায়, এই জটিলতা যদি অপরাপর কোনো উচ্চতর ক্রমের অপেক্ষক (higher order function, i.e., Non-polynomial, e.g., ) হিসেবে বাড়ে, সেইসব সমস্যাকে বহুঘাতেও অনির্ণেয় (NP) শ্রেণীর মধ্যে ফেলা হয় । সমস্যাগুলি স্বভাবতই ‘কঠিন’ এবং সময়সাপেক্ষ । বস্তুত, জরুরী ইনপুট আকারগুলির ক্ষেত্রে (where it really matters, say, ) NP, -এর চেয়ে এতটাই বেশি সময়সাপেক্ষ ( ) যে, প্রকৃতপ্রস্তাবে, এই দুই শ্রেণীর ( & ) সমস্যার গণনাত্মক জটিলতার মধ্যে কোনো সত্যিকারের তুলনাই চলেনা (নিচের ছবিটি দ্রষ্টব্য) । লক্ষণীয়, ইনপুট আকার ১০ থেকেই শুরু হয় এই ভিন্নতা – যা (ইনপুট আকার বাড়ার সাথে সাথে) ক্রমশ শুধু বেড়েই চলে (i.e., two divergent functions) । এই কারণে, কোনো সমস্যাকে সময়ের মধ্যে সমাধান করতে পারা পারতপক্ষে গণনাত্মক গণিতের একটি মস্ত চ্যালেঞ্জ ! প্রসঙ্গত, ‘গ্রাফ রঙ করার সমস্যা’টিও পড়ে বহুঘাতেও অনির্ণেয় কঠিন ( ) সমস্যাগুলির মধ্যে ! এবং এক্ষেত্রে মুনশিয়ানা সেখানেই যেখানে সমাধানটি উত্তম গোত্রের হবে (reasonably accurate) আবার গণণার সময় কমিয়ে আনতে হবে বহুঘাতে নির্ণেয় () সমস্যাগুলির এলাকায় ।

বিশেষ ভাবে উল্লেখ্য, এইরকম ২১ টি কঠিন গণনাত্মক সমস্যা জড়ো ক’রে গণনাত্মক গণিতের অন্যতম কিংবদন্তি মার্কিন বিজ্ঞানী রিচার্ড কার্প ১৯৭২ সালে তৈরী করেন তাঁর বিখ্যাত আগাগোড়া NP সমস্যার তালিকা – যার মধ্যে আমাদের আলোচ্য ‘গ্রাফকে রঙ করার সমস্যাটি’ অন্যতম। মজার কথা হল এই যে, এই ২১ টি সমস্যার যেকোনো একটির সমাধান করতে পারলেই অনুরূপে নাকি বাকি কুড়িটিরও সমাধান সম্ভব।

এক বৈকালিক আড্ডার কথা

তো এ হেন গ্রাফ রঙ করার সমস্যা নিয়ে আজ থেকে দশ বছর আগে এক হঠাৎ পাওয়া আশ্বিন-বিকেলে কাঁকুড়গাছি কবরস্থানে আড্ডায় মেতে উঠেছিল দুই তরুণ ভাবুক – শঙ্কর আর অভিরূপ ! অভিরূপ তখন এন-আই-টি দুর্গাপুরে গণিতের কমপ্লেক্স সিস্টেম নিয়ে এম-টেক করছে, আর শঙ্করের ছিল সাহা ইন্সটিটিউটে পি-এইচ-ডির দ্বিতীয় বছর;   কাজের বিষয় প্রোটিন ফোল্ডিং (গণনাত্মক জীবপদার্থবিদ্যা / Computational Biophysics) !

কোনও একটি নির্দিষ্ট গ্রাফের ক্ষেত্রে তার রঙসংখ্যা কি হবে, তা, ক’ষে বের করা যেহেতু অসম্ভব।

মোদ্দা কথা হল, কেউ তারা সে অর্থে গ্রাফ-থিওরি বিশেষজ্ঞ ছিল না । কিন্তু তাতে কি ! আজ তাদেরই হাতে এই কঠিন সমস্যাটির সমাধানের রূপরেখা গেছে পাল্টে, হয়েছে নতুন দিঙ্মোচন ! নেহাত ভাবাবেগ আর উল্লম্ফন থেকেই যে পথ চলার শুরু, তা, দেখা যাচ্ছে, এ কাজ সে কাজ, এ দেশ সে দেশের ব্যাবধানে দশবছর পর হয়ে দাঁড়িয়েছে এক যাদু-বাস্তবতা, এক অসাধ্য সাধন । কাজটির শেষের দিকে একরকম দৈবযোগেই তারা পেয়ে যায় অমিত’কে (সেকালে, ত্রিপল আইটি এলাহাবাদ) যে বস্তুতই এক গ্রাফ থিওরি বিশেষজ্ঞ ! কাজটির বিভিন্ন জরুরী জায়গায় তার বিশেষজ্ঞ মতামত, তার পূর্ণ সহযোগিতা ব্যাতিরেকে এ কাজের শেষরক্ষা হত না  । 

অতি সম্প্রতি (আগস্ট, ২০১৯) তাদের কাজটি গণনাত্মক গণিতের (Computational Mathematics) অন্যতম সেরা জার্নাল সফট কম্পিউটিং-এ প্রকাশিত হয়েছে ! তারা খুঁজে বের করতে পেরেছে সেই মূল চাবিকাঠি (great key !) যা বস্তুত একটি অবিচ্ছিন্ন (trailing) পথ ও তার সাথে দুটি বিশেষ স্থিতিমাপকের (parameter) নিয়মনীতির (two rules of thumb) অন্তর্লীন সংশ্লেষ । এই প্রস্তাবিত যথাবিহিত নিয়মাবলী ধ’রে একটি গ্রাফকে (অর্থাৎ তার শীর্ষগুলিকে) রঙ করলে যে কোনও ধরনের গ্রাফের ক্ষেত্রেই সেই ন্যূনতম রঙসংখ্যাটির সবচেয়ে কাছাকাছি পৌঁছনো সম্ভব । আবারো স্মরণ করা যাক, যে, কোনও একটি নির্দিষ্ট গ্রাফের ক্ষেত্রে তার রঙসংখ্যা কি হবে, তা, ক’ষে বের করা যেহেতু অসম্ভব – তাই পূর্বোক্ত শর্ত মেনে, যে সেই অজানা ন্যূনতম সংখ্যাটির যত কাছাকাছি পৌঁছতে পারবে, সে ততো সঠিক । 

গ্রাফ তত্ত্ব এবং কম্পিউটার এর যোগাযোগ

কম্পিউটারের প্রথম আমল থেকেই, কিছু বহুচর্চিত অ্যালগোরিদমের (বা মাস্টার প্ল্যানের) মধ্যে গ্রাফ’কে রঙ করার সমস্যাটি উদযাপিত হয়েছে । এই দীর্ঘচর্চার মধ্যে একে একে উঠে এসছে ১) চিনা ডাকপিওনের সমস্যা (Chinese postman problem), ২) ভ্রাম্যমাণ ফেরিওলার সমস্যা (traveling salesman problem), ৩) হ্যানয় সৌধের সমস্যা (Hanoy tower’s problem), ৪) সুদোকু (SuDoKu) – ইত্যাদি জনপ্রিয় গল্পে বাঁধা ধাঁধা !

ফিরে আসা যাক ‘গ্রাফ’কে রঙ করার মূল সমস্যায় – যার বহুবিধ চর্চিত পদ্ধতির মধ্যে (এখনো পর্যন্ত) সবচেয়ে ফলপ্রদ দুটি পদ্ধতি হল – ১) ‘বৃহত্তর আগে বাড়ো ‘ (Largest First: LF) এবং ২) ‘রঙের সম্পৃক্তিই রাঙানোর ভিত্তি’  (DSATUR) পদ্ধতি । যদিও, এযাবৎ এ বিষয়ে গবেষণার পূর্ণচিত্রটি চোখে আঙুল দিয়ে দেখায় যে যেকোনো ধরণের গ্রাফ’কে রঙ করার ক্ষেত্রে এরকম কোনও একটি বিশেষ পদ্ধতি সর্বাত্মকভাবে কার্যকরী হয়ে উঠতে পারেনি । ফলত, এমন একটি অ্যালগোরিদমের প্রয়োজন ছিল যা স্বাধীনভাবে, সম্ভাব্য সমস্ত রকমের গ্রাফের ক্ষেত্রে ‘রঙ-করার-সমস্যাটি’কে উপযুক্ত দক্ষতায় (with desired efficiency) যথাযথভাবে (with optimum accuracy) সমাধান করে ।

আমাদের মূল আলোচ্য শঙ্কর ও অভিরূপের এই অবিচ্ছিন্ন ট্রেইলিং পথের অ্যালগোরিদম (the trailing path algorithm) বা মাস্টার প্ল্যান’টির নকশা বস্তুত এই প্রয়োজনের কথা মাথায় রেখেই বোনা হয়েছিল । বুনতে গিয়ে দেখা গেল বর্তমান অ্যালগোরিদমটি কার্যত পূর্বোক্ত দুটি পরষ্পর নিরপেক্ষ (mutually independent) পদ্ধতির সন্ধানপ্রণালীর সুচিন্তিত সংকরায়ণ (a meticulous amalgamation of the two search patterns of LF & DSATUR) । 

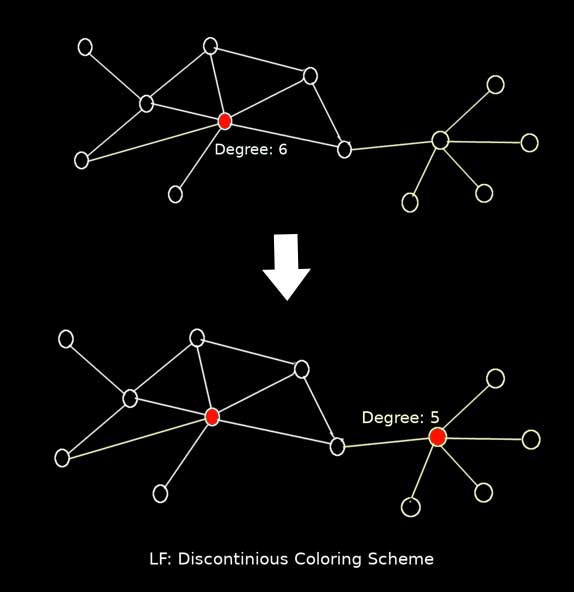
“বৃহত্তর আগে বাড়ো” LF (Largest First) হল একটি গ্রাফের শীর্ষের যোজ্যতার অধঃক্রমে (in the descending order of degrees of nodes) রঙ করতে করতে যাওয়া । অর্থাৎ যদি কোনো গ্রাফের সর্বাধিক যোজ্যতাবিশিষ্ঠ শীর্ষটির যোজ্যতা ৫ হয়, তবে তাকে রঙ দিতে হবে চতুর্যোজী শীর্ষগুলির আগে এবং এভাবে রঙ করতে করতে যদি একাধিক একই যোজ্যতাবিশিষ্ট শীর্ষ পাওয়া যায় সেক্ষেত্রে তাদের রঙ দিতে হবে বিধিবহির্ভূতভাবে ইচ্ছামত (randomly or arbitrarily) !

রঙসংখ্যা বা ক্রোম্যাটিক নাম্বারের তাত্বিক উর্দ্ধসীমা (theoretical upper limit) গ্রাফটির শীর্ষের সংখ্যা।

সহজেই অনুমেয় যে এভাবে রঙ করার পদ্ধতিটি বিচ্ছিন্ন (discontinuous coloring scheme) বা অন্যকথায় এভাবে ক্রমান্বয়ে রঞ্জিত শীর্ষগুলি যে গ্রাফ বরাবর একটি যুক্ত পথের হদিশ দেবে এমন কোনো গ্যারাণ্টি নেই। বরং শতকরা ৯৯ ভাগ ক্ষেত্রেই তেমনটা হবেনা (নিচের ছবিটি দ্রষ্টব্য); হলে নেহাতই হবে ভাগ্যবলে (purely by chance) !

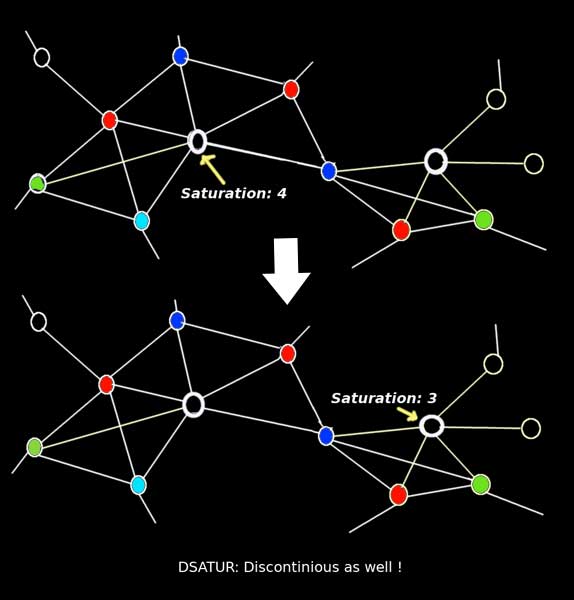
DSATUR

DSATUR বা ‘রঙের সম্পৃক্তিই রাঙানোর ভিত্তি’ -এ ‘SATUR’ কথাটি আসছে ‘SATURATION’ বা সম্পৃক্তি থেকে । কিসের সম্পৃক্তি ? রঙের । কি অর্থ এই কথার ? প্রথমেই মাথায় রাখতে হবে গ্রাফ রঙ করার ক্ষেত্রে একটি শীর্ষ লাল (বা হলুদ – যা খুশি) রঙ পেলে তার সঙ্গে যুক্ত শীর্ষগুলি কখনোই আর সেই লাল (বা হলুদ) রঙটি পাবেনা । এই মূল শর্তটি মাথায় রেখে এই পদ্ধতিতে কোনো গ্রাফকে রঙ করার ক্ষেত্রে প্রতিটি ধাপে তাদের শীর্ষগুলির কোনটিকে কোন রঙ আর কিছুতেই দেওয়া চলবেনা তার জরিপ রাখা হয় । এখন, রঙসংখ্যা বা ক্রোম্যাটিক নাম্বারের তাত্বিক উর্দ্ধসীমা (theoretical upper limit) যেহেতু গ্রাফটির শীর্ষের সংখ্যা বই আর কিছু নয় (যেহেতু ১০ টি শীর্ষের গ্রাফকে রঙ করতে কোনো অবস্থাতেই ১১ টি রঙ লাগতে পারেনা), তাই, একটি গ্রাফের কোনো শীর্ষকে এই ‘দেওয়া চলবেনা রঙের সংখ্যা’ পারতপক্ষে বোঝায় ওই শীর্ষটির রঙের সম্পৃক্তি । অর্থাৎ কোন শীর্ষটি ওই ‘দেওয়া চলবেনা রঙের সংখ্যার’ বিচারে কতটা সম্পৃক্ত বা রঙসংখ্যার পূর্বোক্ত তাত্বিক উর্দ্ধসীমার কত কাছাকাছি ! সেই হিসেবে যে শীর্ষটি (দেওয়া চলবেনা এমন রঙের দ্বারা) বেশী সম্পৃক্ত তাকে আগে রঙ করতে হবে, এবং এই রঙ করা চলবে এই রঙের সম্পৃক্তির অধঃক্রমে । স্বাভাবিকভাবেই, এভাবে রঙ করার পদ্ধতিটিও বিচ্ছিন্ন (discontinuous coloring scheme) । অর্থাৎ পরের ধাপে রঞ্জিত শীর্ষটি যে আগের ধাপে রঞ্জিত শীর্ষটির সঙ্গে যুক্ত থাকবে, এমন কোনো বাধ্যবাধকতা নেই (নিচের ছবিটি দ্রষ্টব্য)।

ফিরে আসা যাক, আমাদের মূল আলোচ্য, অবিচ্ছিন্ন ট্রেইলিং পথের অ্যালগোরিদমটিতে (the trailing path algorithm) । নাম থেকেই অনুমেয় যে এটি একটি অবিচ্ছিন্ন (ট্রেইলিং) পথ ধরে (কিছু সুনির্দিষ্ট নিয়ম মেনে) গ্রাফ (বা তার শীর্ষগুলিকে) রঙ করার পদ্ধতি । অর্থাৎ কোনো একটি ধাপে রঙ করার জন্যে বেছে নেওয়া শীর্ষটিকে অতিঅবশ্যই ঠিক তার আগের ধাপে রঞ্জিত শীর্ষটির সাথে যুক্ত থাকতে হবে । এবং এইদিক দিয়ে বিচার করলে অ্যালগোরিদমটির অবস্থান মৌলিক এবং উপরোক্ত পদ্ধতিদুটির সম্পূর্ণ বিপরীতে । মজার কথা হচ্ছে, এই মূল বৈপরীত্য রেখেও  একইসাথে অ্যালগোরিদমটি আবার ওদেরই (LF & DSATUR) সন্ধানপ্রণালী-দুটির সুচিন্তিত সংকরায়ণ !

অবিচ্ছিন্ন ট্রেইলিং পথের অ্যালগোরিদম

গোটা ব্যাপারটা তাহলে ঠিক কিরকম ?

১) প্রথমেই ঠিক (conventionalize) করে নিতে হবে একটি সুনির্দিষ্ট  রঙ-যাজকতন্ত্র (color hierarchy) অর্থাৎ, রঙ-ক লভ্য (available) হ’লে ক’-কেই নিতে হবে, ক অলভ্য হ’লে তখন ডাক পড়বে রঙ-খ’এর, খ’ অলভ্য হ’লে গ-এর – এভাবে  । ক’ হাজির থাকলে খ’কে কোনওভাবেই বাছা যাবেনা ।  অন্য  কথায়, লাল > কমলা > হলুদ > সবুজ > আশমানি > নীল > বেগুনি; বা, উল্টোটা । অর্থাৎ যা হয় একটা কোনো ক্রম, আগে থেকে ঠিক করে নেওয়া চাই । যা-ই ঠিক করা হোক, একটি বা একগুচ্ছ গ্রাফের আগাগোড়া রঙ করার মধ্যে এই ‘কে বেশী রঙিনের ক্রম’টিকে আর পাল্টানো যাবেনা । 

২) এবার, যেকোনো একটি প্রদত্ত গ্রাফের ক্ষেত্রে প্রথমেই খুঁজে বের করে নিতে হবে কোন শীর্ষের বাহুর সংখ্যা সর্বোচ্চ – অন্যকথায়, কোনটি সবচেয়ে বেশি সংযুক্ত শীর্ষ (the maximally connected node) । সেটিকে চোখ বন্ধ করে পূর্বনির্ধারিত রঙ-যাজকতন্ত্রের প্রথম রঙটি (ধরা যাক, লাল) দিয়ে রাঙাতে হবে । স্বাভাবিকভাবেই, এই উচ্চ যোজ্যতার শীর্ষটির সাথে সংযুক্ত বাকি শীর্ষগুলিকে আর ওই রঙটি (লাল) দিয়ে রাঙানো চলবেনা (যেহেতু যুক্ত শীর্ষগুলিকে একই রঙ দেওয়া চলবেনা) । এর অব্যবহিত পরেই, লাল রঙে যে রাঙানো চলবে না, এই তথ্যটি পৌঁছে দিতে হবে যুক্ত শীর্ষগুলির দ্বারে দ্বারে । যাতে ক’রে, পরেরবার রঙের মিস্ত্রি এলে সে রঙ চিনতে ভুল না ক’রে বসে । যাতে ক’রে, প্রতিটি শীর্ষ’কে রঙ দেওয়ার ক্ষেত্রে লভ্য রঙগুলির নির্ভুল তালিকা তার হাতে আসে । এর জন্যে প্রথমেই গ্রাফটির প্রতিটি শীর্ষের সঙ্গে জুড়ে দিতে হবে একটি রঙ-তথ্যের খালি খেরোখাতা (an empty color-info-array) । এবং একেকবার একেকটি শীর্ষ’কে একেকটি রঙে রাঙানোর পর তার সঙ্গে যুক্ত শীর্ষগুলির আপন আপন খেরোখাতার একেকটি পাতায় লিখে রাখতে হবে ওই ওই রঙগুলির নাম । লেখা শেষ হলে রঞ্জিত শীর্ষটিকে তার বাহু সমেত মুছে ফেলতে হবে । প্রতিটি ধাপে এই রঙ দেওয়া ও মুছে ফেলার পর, ফলত, একেকটি নতুন গ্রাফ জন্ম নেবে ।

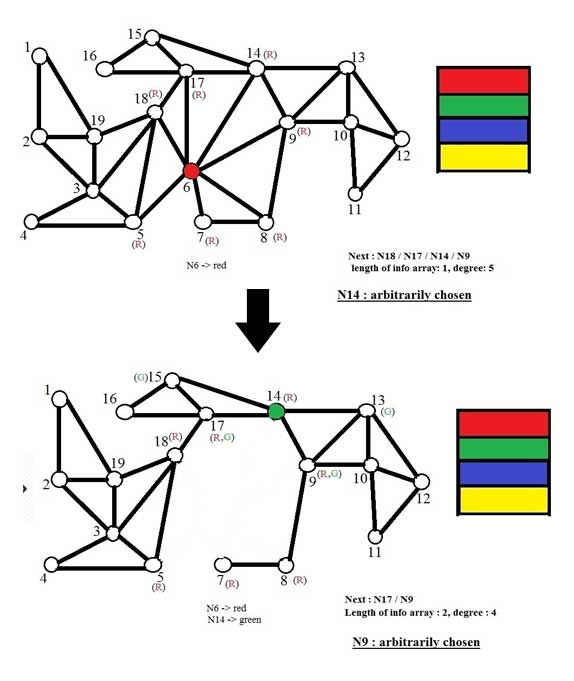
৩) এরপর স্বাভাবিক ভাবেই প্রশ্ন এসে পড়ে যে কোন পথ (path) ধ’রে এই ক্রমান্বয়ে রঙ করা চলতে থাকবে ! এখানে, অ্যালগোরিদমটির প্রথম নিয়মটি (যা তার একটি মৌলিক ও বিশেষ বৈশিষ্ট্য)  তৈরী করা হল এই, যে এই ‘পথ’ হতে হবে অবিচ্ছিন্ন (trailing) ।

উচ্চ-যোজ্যতা সম্পন্ন  শীর্ষর অগ্রাধিকার এবং তারপর রঙের সম্পৃক্তি – এই দুইটি নিয়মই মেনে চলতে হবে।

অর্থাৎ যেকোনো একটি শীর্ষকে রঙ করার পর, শুধুমাত্র তার সঙ্গে যুক্ত শীর্ষগুলিকেই পরের ধাপে রঙ করার জন্যে বেছে নেওয়া যেতে পারে – দূরের কোনও বিযুক্ত শীর্ষকে বাছা চলবেনা । এবং, এই অবিচ্ছিন্ন পথটির নথি রাখতে হবে রঞ্জিত শীর্ষগুলির একটি অনুক্রম (sequence) হিসেবে । যদি, একান্তই আর কোনও যুক্ত শীর্ষ অবশিষ্ট না থাকে তবে গ্রাফটি কতকগুলি অসংলগ্ন গ্রাফ-উপাংশের সংগ্রহে (collection of disjoint components or sub-graphs) পর্যবসিত হবে এবং সেক্ষেত্রে তাদের যেকোনো একটি থেকে আবার নতুন করে রঙ করা শুরু করতে হবে । 

৪) এবার, এই অবিচ্ছিন্ন পথ ধরে রঙ করতে করতে এগোনোর জন্য চাই একটি শীর্ষ-নির্বাচন নীতি (selection rule for the node to be colored next) ! অর্থাৎ, একটি শীর্ষকে রঙ করার পরের ধাপে তার সঙ্গে যুক্ত সম্ভাব্য একাধিক শীর্ষের মধ্যে কোনটিকে বেছে নেওয়া হবে, তার কি নিয়ম ! এখানে সামিল করা হল দুটি গ্রাফরঙ-স্থিতিমাপক (graph coloring parameters): (১) শীর্ষের যোজ্যতা (degree) – অর্থাৎ, একটি শীর্ষ কতগুলি অন্য শীর্ষ’র সাথে যুক্ত, সেই সংখ্যা, আর, (২) রঙের সম্পৃক্তি: অর্থাৎ গ্রাফ রঙ করার যেকোনো ধাপে কতগুলি রঙ একটি শীর্ষকে দেওয়া চলবেনা বলে ইতমধ্যেই নির্ধারিত হয়েছে, এবং যার পরিমাপ রাখা হয়েছে ওই শীর্ষের সঙ্গে সংযুক্ত পূর্বোক্ত রঙ-তথ্যের খেরোখাতাটির ব্যবহৃত পৃষ্ঠার সংখ্যা  দিয়ে (i.e., the length of the color-info-array) ! এর মধ্যে প্রথম নির্নায়কটি হল শীর্ষের যোজ্যতা – যার অধোগামী ক্রমে (descending order of degree) যেতে হবে ! অর্থাৎ সম্ভাব্য দুটি শীর্ষের মধ্যে উচ্চ-যোজ্যতা সম্পন্ন  শীর্ষটি অগ্রাধিকার পাবে অপেক্ষাকৃত নিম্ন- যোজ্যতা সম্পন্ন শীর্ষটির চেয়ে ! তাতে ক’রে যদি কোনও ধাপে দুটি শীর্ষের যোজ্যতা সমান হয়ে যায় (‘tie’ in degree), তাহলে ডাক পড়বে দ্বিতীয় স্থিতিমাপক অর্থাৎ রঙের সম্পৃক্তির । একই যোজ্যতার সেই শীর্ষটি অগ্রাধিকার পাবে যে বেশী সম্পৃক্ত । ব্যাস । নিয়ম শুধুমাত্র এ দুটিই । এরপরেও যদি একাধিক সম্ভাবনা থেকে যায়, অর্থাৎ, একাধিক শীর্ষের মধ্যে উভয় স্থিতিমাপকের মান’ই ঘটনাচক্রে সমান হয়ে যায়, তখন যেকোনো একটি শীর্ষকে বিধিবহির্ভূতভাবে ইচ্ছামত (randomly or arbitrarily) বেছে নিতে হবে ! আর এভাবেই অ্যালগোরিদমটি হয়ে দাঁড়াল পূর্বোক্ত বিচ্ছিন্ন  (discontinuous) পদ্ধতিদুটির (LF & DSATUR) সন্ধানপ্রণালীর সুবিবেচনাপূর্ণ সংমিশ্রণ । স্বাভাবিকভাবেই, এভাবে এই অবিচ্ছিন্ন পথানুসরণ ক’রে একটানা রঙ করতে থাকলে (following a continuous coloring scheme) কখনোই কোনও গ্রাফের ক্ষেত্রে পাশাপাশি বা যুক্ত দুটি শীর্ষ (connected / adjacent nodes) এক রঙ পাবেনা এবং শুধু তাই নয়, ন্যূনতম রঙ খরচ করেই গ্রাফটিকে রঙ করা সম্ভব হবে । অন্য কথায়, হদিশ মিলবে, ক্রোম্যাটিক নাম্বার বা যথার্থ রঙ-সংখ্যাটির ! উপরন্তু এভাবে রঙ করার আরেকটি সুবিধে হল এই যে কোনও ধাপে যদি গ্রাফটি উপাংশে বিশ্লিষ্ট (split into disjoint components) হয়, তখন তাদের একাধিক উপাংশকে একসাথে বা একধাপে রঙ করলেও ক্ষতি নেই – যেহেতু তাদের রঙ করার সমস্যা পরষ্পর নির্ভরশীল নয়, বা, অন্য কথায় স্বাধীন ! সেভাবে কম্পিউটার কোড’টি লিখতে পারলে এতে করে সময়েরও সাশ্রয় ।

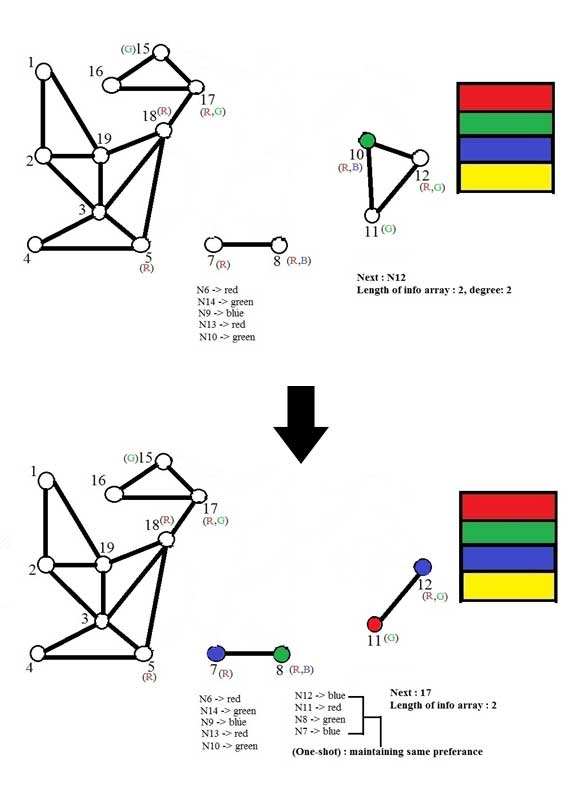
এমনও হতে পারে যে কোনও একটি অবিচ্ছিন্ন পথ বরাবর রঙ করতে করতে পৌঁছে গেছি একেবারে প্রান্তশীর্ষে ! অথচ, পাখীর চোখ দিয়ে দেখলে (from a ‘birds eye view’) স্পষ্টতই ধরা পড়বে যে অন্য প্রান্তগুলি তখনও রঙ পায়নি । সেক্ষেত্রে, লেনিনের ‘এক-পা এগোনোর জন্যে গোড়ায় দুই পা পিছনোর থিওরি’র মতোই করতে হবে পশ্চাদাপসরণ (back-track), যতক্ষণ না সেই অবিচ্ছিন্ন পথের (trailing path) সংলগ্ন কোনও অরঞ্জিত শীর্ষ অবশিষ্ট থাকে । 

বিশেষভাবে এও উল্লেখ্য, যে রঙ করার প্রতিটি ধাপেই যেহেতু (স্থিতিমাপক দুটির বিচারে অভিন্ন) একাধিক শীর্ষের অনুরূপ জোরালো আবেদন থাকতে পারে, বা, অন্যকথায়, প্রতি রাস্তার মোড়েই যেহেতু একাধিক পথের সমতুল অহ্বান থেকে যায়, তাই একই গ্রাফের ক্ষেত্রে ন্যূনতম রঙসংখ্যাটিকে অক্ষুণ্ণ রেখেও নানান বিকল্প শীর্ষ – ও – রঙের সম্বন্ধ (degenerate alternative mapping of “node → color”) তৈরী হবার মুক্ত সম্ভাবনা থেকে যায়।  অর্থাৎ, যুগপৎ, ‘যত মত তত পথ’, আবার, ‘সব পথ শেষে / মিলে গেল এসে / তোমারই দুখানি নয়নে …’  উদাহরণ হিসেবে আমরা নিচের ছবিটি নিতে পারি – যেখানে রঙ করার (শুধুমাত্র) দ্বিতীয় ধাপেই এরকম চারটি সম্ভাবনা পাওয়া যায় ! বলা বাহুল্য, পরবর্তী ধাপগুলিতে এই সম্ভাবনা ক্রমবর্ধমান । যদিও, এর প্রতিটি পথ ধরে রঙ করা শেষ করলে শেষটায় দেখা যাবে, যে, ক্রোম্যাটিক নাম্বার বা রঙসংখ্যা প্রতিটি ক্ষেত্রেই, ‘তিন’ – যা কিনা অব্যর্থ ও ন্যূনতম ।

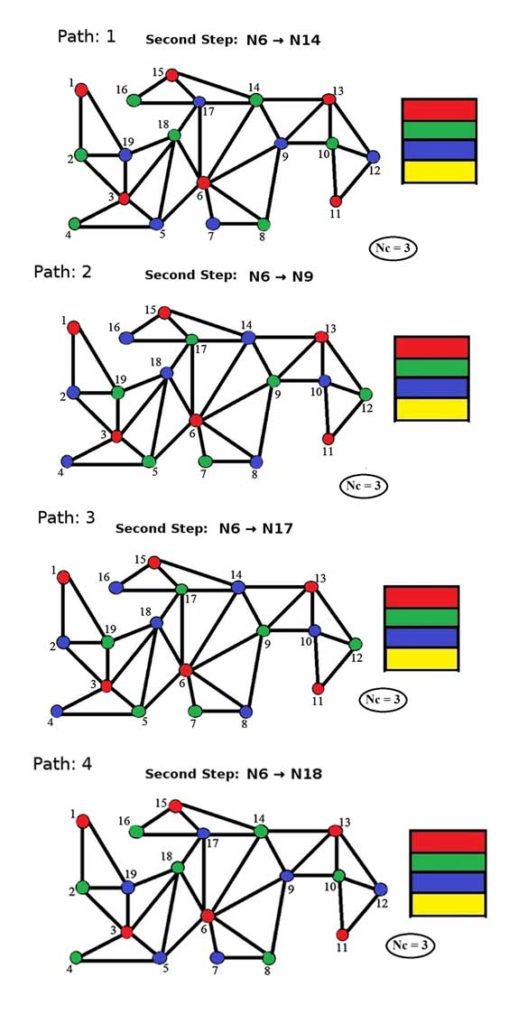
অ্যালগরিদমটিকে বাস্তবায়িত করতে ব্যাবহৃত হয়েছে MATLAB (MATrix LABoratory) এবং ছাত্র-বান্ধব অবানিজ্যিক অনুরূপ ইন্টারফেস ‘Octave’ ! Chromnum কম্পিউটার কোড’টি বিনামূল্যে যে কেউ ডাউনলোড করে চালাতে পারেন নিজের সিস্টেমে  । 

অ্যালগোরিদমটির গণনামূলক সুবিধা

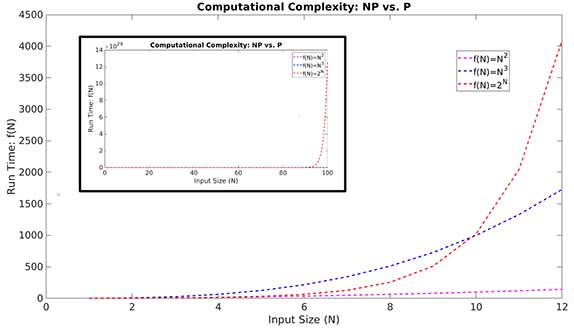
রঙসংখ্যার গণনার ক্ষেত্রে সবচেয়ে কঠিন ও জটিল গ্রাফগুলি হল নিয়মিত গোত্রের (regular graphs) – কেননা তাদের প্রতিটি শীর্ষের যোজ্যতা সমান – ফলত দুটি পূর্বনির্ধারিত স্থিতিমাপকের একটির নিরিখে (শীর্ষের যোজ্যতা) তারা গোড়াতেই এক স্তরের অভেদ রচনা করে বসে আছে ! রইল বাকি অন্য স্থিতিমাপক’টি – যা কিনা – রঙের সম্পৃক্তি । ফলত, রঙ করতে গিয়ে দুই বা ততোধিক শীর্ষের মধ্যে সর্বস্তরের অভেদ বস্তুত হামেশাই রচিত হতে পারে, এবং, সেক্ষেত্রে, প্রতিবার, অ্যালগরিদমটির নির্ধারিত নিয়মানুযায়ী একটি ইচ্ছেমত শীর্ষকে বেছে নিয়ে এগোতে হবে ! এভাবে সম্ভাব্য সবগুলি ইচ্ছেমত পথ দেখেশুনে ঘুরে এসে তার মধ্যে ন্যূনতম রঙসংখ্যার পথটি বেছে নিতে হলে গণনার জটিলতা বাড়তে বাড়তে বহুঘাতেও অনির্ণেয় (Non-deterministic in Polynomial time: NP-Hard) ধরণের কঠিন সমস্যার তালিকায় পড়ার গুরুতর সম্ভাবনা থেকে যায় ! এই জট ছাড়াতে ব্যাবহার করা হয় (সময়ের) খরচ (computational cost) ও দক্ষতার (efficiency / accuracy) একটি যথোপযুক্ত দাঁড়িপাল্লা (trade-off) ! পদ্ধতিগত ভাবে গ্রাফটিকে প্রথম থেকে শেষ পর্যন্ত পূর্বনির্ধারিত একটি সসীম বড় সংখ্যা (a fixed finite large number) পর্যন্ত বারবার (in an iterative manner) রঙ করা হয় এবং নেওয়া হয় তার মধ্যে ন্যূনতম রঙসংখ্যার পথ’টি । এরকম অসংখ্য নিয়মিত গ্রাফের ওপর গণনা করে দেখা গেছে যে, অপরাপর পদ্ধতিগুলির তুলনায় নির্ভুল ও দ্বর্থ্যহীন ভাবে ট্রেলিং পথের অ্যালগরিদমটি এমনকি এই আপাত কঠিন গ্রাফগুলির ক্ষেত্রেও অপেক্ষাকৃত সঠিক (অর্থাৎ নিম্নতর) রঙসংখ্যাটিকে তুলনায় অনেক কম খরচে খুঁজে বের করতে সক্ষম, এবং গণনার জটিলতাও অনায়াসেই বহুঘাতে নির্ণেয় (NP → P) – র পরিধির মধ্যে পড়ে  (নিচের ছবিটি দ্রষ্টব্য) ।

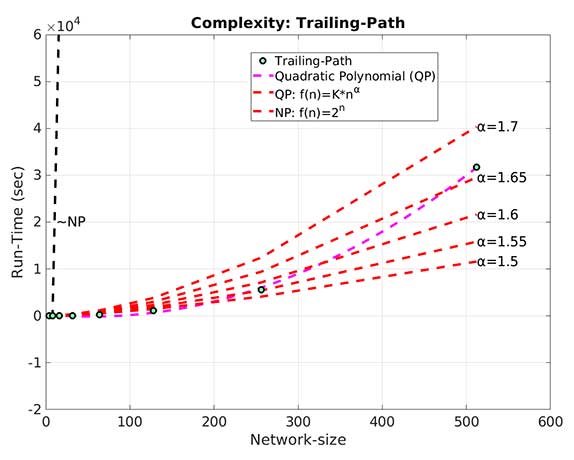
উপরের ছবিটির বাঁদিকে প্যানেলে পরীক্ষিত গণনাত্মক জটিলতাকে (calculated computational complexity, ) নীল কাটা কাটা রেখায় (the blue dashed line) প্লট করা হয়েছে নিয়মিত গ্রাফের আকারের (size: ) অপেক্ষক হিসেবে – যা একটি দ্বিঘাত সমীকরণকে নির্দেশ করে । যেখানে ২-এর সাধারণ অনুপাতের গুণোত্তর প্রগতিতে নির্মিত ৪ থেকে ৫১২ শীর্ষের নিয়মিত গ্রাফের প্রস্তাবিত রঙসংখ্যা পাওয়া যাচ্ছে যথাক্রমে ২, ৪, ৬, ১১, ২২, ৪৫, ৮৯, ১৭৮ ! লাল রেখা গুলি বহুঘাতের অপেক্ষকটির ভগ্নাংশ ঘাত (α) কে চিহ্নিত করে যেগুলি জটিলতার পরিলেখটিকে (complexity profile) আচ্ছাদিত (envelope) করতে প্লট করা হয়েছে – যার নিরিখে, গণনাত্মক জটিলতার সবচেয়ে কাছের (optimal) ঘাত’টি দেখা যাচ্ছে ১.৭ ! 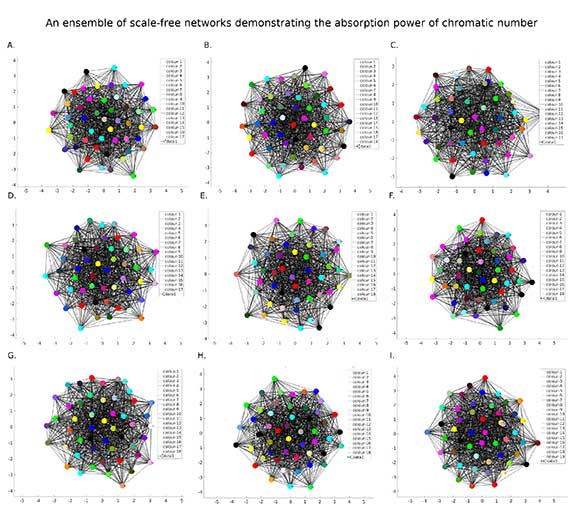বিশেষভাবে লক্ষনীয় এই যে বহুঘাতেও অনির্ণেয় ( ) জটিলতার পরিলেখ’টি (কালো রেখা) গোড়াতেই হু হু করে বেড়ে অচিরেই অন্তর্ধান করেছে প্লট থেকে ।  বিজ্ঞানের প্রচলিত ভাষা নিয়েও কিছু প্রশ্ন তুলে ধরার চেষ্টা করা হয়েছে পেপারটিতে। নানাবিধ গ্রাফের (small-world:  যুক্ত-জগত, scale-free: পাল্লা-মুক্ত, modular: শাখান্বিত, regular: নিয়মিত, random: যা-খুশি) ক্ষেত্রে ধ’রে ধ’রে নিয়মানুগভাবে রঙসংখ্যার গণনা করতে গিয়ে নিশ্চিত হওয়া গেছে ‘রঙসংখ্যা’ – এই গ্রাফ-ধর্মটির বিস্ময়কর স্থায়িত্ব আর ধারণক্ষমতা (stability and absorptive property of graph coloring) সম্বন্ধেও ! উদাহরণ স্বরূপ বলা যায় নিচের বিমিশ্র ছবিটিতে (composite figure) প্রদর্শিত পাল্লা-মুক্ত গ্রাফের সংকলনটির কথা – যেখানে গ্রাফগুলির প্রতিটির আকার ৫০ (অর্থাৎ, প্রতিটি গ্রাফ ৫০ টি শীর্ষ দিয়ে গড়া), এবং তাদের শীর্ষগুলির গড় যোজ্যতা ৪১ থেকে ৪৯ ওব্দি বাড়ানো হয়েছে । যার ফলে তাদের বাহুর সংখ্যা  ৮৮৫ থেকে  বেড়ে  হয়েছে  ৯৬৭, অথচ, যাদের (ন্যূনতম) রঙসংখ্যা বেড়েছে মোটে ১৭ থেকে ১৯ ।  অর্থাৎ নতুন ৮২ টি বাহু’কে ধারণ করতে লেগেছে মাত্র দুটি নতুন রঙ ।

আশার আলো – ব্যবহারিক প্রয়োগ

পেপারটিতে “গ্রাফ রঙ করার” নানান ব্যাবহারিক প্রয়োগ আলোচিত হয়েছে – যার মধ্যে সবচেয়ে  বিশদালোচিত হয়েছে বায়োফিজিক্সের আরেকটি অন্যতম জরুরী, ব্যাবহারিক ও কঠিন সমস্যা – ইচ্ছে ও প্রয়োজন মতো প্রোটিনের নক্সা তৈরীর (protein design) ক্ষেত্রে রঙসংখ্যার সম্ভাব্য ব্যাবহারের কথা ।  এছাড়াও বহুস্তরের (জাতীয় / আন্তর্জাতিক / স্থানীয়) সুরক্ষা ও নজরদারীর (security / surveillance) ক্ষেত্রে, কোলকাতার মতো মহানগরের যানজট নিয়ন্ত্রণের ক্ষেত্রে, একটি রসায়নাগারের নক্সা তৈরীর ক্ষেত্রে (যেখানে দুটি বিশেষ গ্যাসের সংযোগে বিস্ফোরণের সম্ভাবনা থেকে যায়) – বস্তুত যেকোনো ধরণের বিভাজনগত সমস্যার (partitioning problem) ক্ষেত্রেই “গ্রাফ রঙ করার সমস্যাটির” ব্যাবহার সুদূর সম্ভাবনাময় !

বর্তমানে, অভিরূপ ফ্রান্সের মার্সেই শহরে, ‘ইন্সটিটিউট দে নিউরোসাইন্সেস দে লা টাইমন’ – এ পোষ্টডক্টরাল স্তরে গবেষণারত, শঙ্কর আশুতোষ কলেজে, অমিত আই-আই-টি ভিলাইয়ে অধ্যাপনারত । এই আর্যভট্ট, নাগার্জুন, মাধবা, রামানুজনের দেশের জলহাওয়ায় বড় হতে পেরে শঙ্কর (ডঃ শঙ্কর বসু), অভিরূপ (ডঃ অভিরূপ বন্দ্যোপাধ্যায়), অমিত (ডঃ অমিত কুমার ধর) চিরকৃতজ্ঞ । এই কাজটি তাদের অপরিশোধ্য গুরুঋণের প্রতি সেই বিনম্র কৃতজ্ঞচিত্তের উৎসর্গ ।

প্রচ্ছদের ছবি: Bandyopadhyay, A., Dhar, A.. & Basu, S. Soft Comput (2020) 24: 603.

https://doi.org/10.1007/s00500-019-04278-8 উপযুক্ত স্বত্ব-অনুমতি সহ মূল পেপার থেকে সংগৃহিত ও পরিমার্জিত

টীকা :

বিনিমেয় পরিভাষা (Interchangeable terms):
১) গ্রাফ / নেটোয়ার্ক
২) শীর্ষ / নোড / ভার্টেক্স
৩) বাহু / এজ / লিঙ্ক
৪) যোজ্যতা / ডিগ্রি

পথ – গ্রাফ থিওরিতে পথ (path) বলতে বোঝায় সংযুক্ত শীর্ষ ও সংলগ্ন বাহুগুলি ছুঁয়ে ছুঁয়ে চলা একটি ক্রম ।

পরিশিষ্ট

• কাজটির সংবাদমাধ্যম সম্প্রচারের একটি দলিল (media coverage) পাওয়া যাবে নিচের লিঙ্কে – https://www.anandabazar.com/others/science/three-bengali-scientist-achieved-success-in-combinatorial-optimization-or-combinatorics-1.1058891
• একটি মৌখিক উপস্থাপনাও (talk) পাওয়া যাবে নিচের লিঙ্কে – https://www.youtube.com/watch?v=r33EC4DAMUA

বিজ্ঞানকৃত বাংলা সাবটাইটেলে ‘কোয়েনিসবার্গের সাতটি ব্রিজের সমস্যা’

লেখাটা পড়তে এখানে ক্লিক করো

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/trailing-the-chromatic-numbers

print