21-12-2024 16:59:28 pm

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

প্রতিক্রিয়া আর টানের ব্যাখ্যা: কিছু জটিল সমস্যা

ধীরঞ্জন রায়

(যাদবপুর বিশ্ববিদ্যালয়)

26 Feb 2021

Link: https://bigyan.org.in/tension-reaction-complex-problems

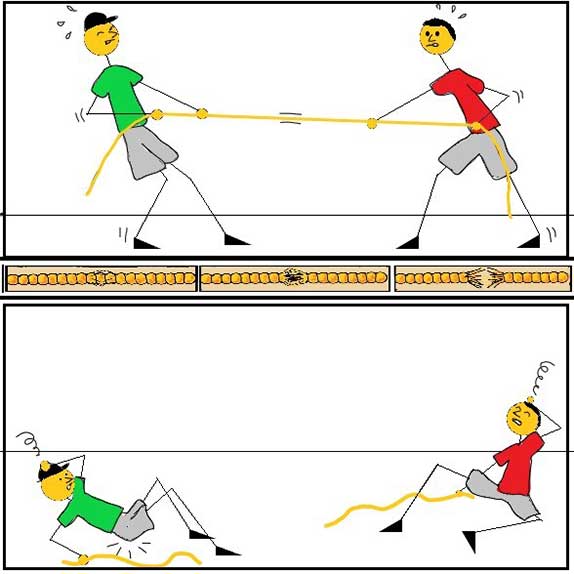
%e0%a6%aa%e0%a7%8d%e0%a6%b0%e0%a6%a4%e0%a6%bf%e0%a6%95%e0%a7%8d%e0%a6%b0%e0%a6%bf%e0%a7%9f%e0%a6%be-%e0%a6%86%e0%a6%b0-%e0%a6%9f%e0%a6%be%e0%a6%a8%e0%a7%87%e0%a6%b0-%e0%a6%ac%e0%a7%8d%e0%a6%af

ভরহীন সুতোয় টানের অঙ্ক কষা যত সোজা, সে সুতো না হয়ে দড়ি হলে আর দড়ির ভর ধরতে হলে তখন আর ব্যাপারটা অতটা সোজা থাকে না। একে তো সেই দড়ির সর্বত্র টান (tension) একই হয়না। তার ওপর সে দড়ি যদি আগাগোড়া একইরকম না হয়, তখন সমস্যাটা আরো কঠিন হয়ে যায়। অথচ সে দড়ি না হয়ে হালকা সুতো হলে তাকে একেবারে ভরহীন ধরে যে উত্তর পাওয়া যায়, সেটা খুব একটা ভুল না। এরকম সরলীকরণ কখন খাটে আর কখন খাটে না, সেই নিয়ে আলোচনা করেছেন পদার্থবিদ্যার অধ্যাপক ধীরঞ্জন রায়।

আগের পর্বে জমির প্রতিক্রিয়া আর টান নিয়ে আলোচনা করা হয়েছিল। এই পর্বে সেই টানের অঙ্কটাকেই আরেকটু প্যাঁচালো করা হলো।

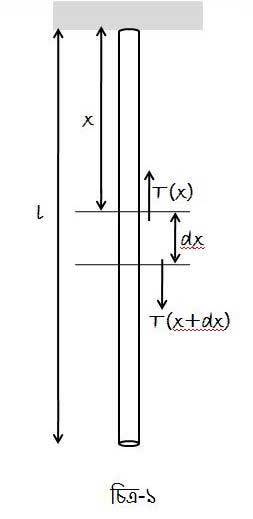
ধরা যাক, $m$ ভর এবং দৈর্ঘ্যের একটি সুতো উল্লম্বভাবে একটি কীলক (pivot) থেকে ঝোলানো হল (চিত্র-১)। এটাও ধরা যাক যে সুতোটা আগাগোড়া একইরকম। এখন প্রশ্ন হলো, এই সুতোর কোন এক বিন্দুতে কিরকম টান অনুভূত হবে?

ধরা যাক, সুতোর বিন্দুর নিচের অংশে একটা বল প্রয়োগ করা হলো সুতোর সাম্যাবস্থা বজায় রাখার জন্য। সুতরাং

$T(x)= \frac{mg}{l}(l-x)= mg(1-\frac{x}{l})$

যেখানে

$\frac{m}{l}=\rho$

অর্থাৎ সুতোর রৈখিক ঘনত্ব (linear density) সর্বত্র সমান ধরা যেতে পারে।

এখন প্রশ্ন হলো, যদি সুতোটা আগাগোড়া একইরকম না হয়, তাহলে এই টান কিভাবে গণনা করা যাবে? সেক্ষেত্রে, সুতোর রৈখিক ঘনত্ব $\rho$ -এর মান সুতোর কোনখানটা ধরছি, তার উপর নির্ভর করবে। অর্থাৎ, ঘনত্বটাকে এবার $\rho(x)$ বলতে হবে। তবে সুতোটাকে অনেকগুলি ছোট ছোট অংশের সমষ্টি বলে ধরা যেতে পারে এবং একেকটা ছোট অংশের মধ্যে সুতোটার পরিবর্তন উপেক্ষা করা যেতে পারে। সুতোর $x$ এবং $(x+dx)$ বিন্দুতে টান যদি যথাক্রমে $T(x)$ এবং $T(x+dx)$ হয়, সাম্যবস্থা বজায় রাখার জন্য নিচের সমীকরণটি মেনে চলতে হবে।

$T(x)= T(x+dx) + \rho(x)gdx$

বা

$\frac{dT}{dx}= -\rho(x)g$

এখানে $\rho(x)$ জানা থাকলে ওপরের ডিফারেনশিয়াল সমীকরণ সমাধান করা যাবে। এরকম একটা সমীকরণের সম্পূর্ণ সমাধান করতে কোথাও একটা টান জানা থাকা প্রয়োজন। এটাকে প্রাথমিক শর্ত (initial condition) বলে। ধরা যাক, সুতোর নিচে কিছু ঝুলে নেই। তাহলে, সুতোর মুক্ত প্রান্তে কোন টান অনুভূত হবে না। এই শর্তটি অর্থাৎ

$T(l)= 0$

প্রয়োগ করলে $T(x)$ এর একটি ফর্মুলা পাওয়া যাবে (কষে দেখ)। সেই ফর্মুলাতে যদি আগের সেই সর্বত্র সমান ঘনত্বের সুতো বসিয়ে দি, অর্থাৎ যদি

$\rho(x)= \frac{m}{l}$

বসাই, তাহলেও আগের সমাধানে ফিরে যাওয়া যাবে (তোমার সমাধানটা ঠিক হলো কিনা, সেটাও যাচাই করতে পারবে)।

দড়ি ধরে মারো টান

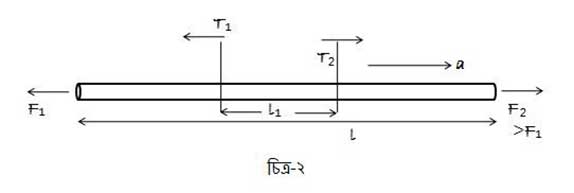
এতক্ষণ পর্যন্ত আমরা শুধু সাম্যবস্থায় থাকা স্থির সুতোর কথাই ধরেছি। এবার দড়ি টানাটানি খেলার কথা দেখা যাক, যেখানে দড়ি একবার এদিকে যাচ্ছে, একবার ওদিকে (চিত্র-২)। দড়ির দুই প্রান্তে যথাক্রমে $F_{1}$ এবং $F_{2}$ বল প্রয়োগ করা হলো, যেখানে

$F_{2}>F_{1}$

একদিকের বল বেশি হওয়ার কারণে সুতোটি কিছুটা সেইদিকে সরে যাবে সাম্যবস্থায় পৌঁছানোর জন্য। অর্থাৎ সেদিকে তার একটা ত্বরণ (acceleration) সৃষ্টি হবে। যদি দড়ির ভর $m$ হয় এবং সুতোটির ডানদিকে $a$ ত্বরণ থাকে তাহলে:

$F_{2} - F_{1}= ma$

এটা গেল সম্পূর্ণ দড়িটা কিভাবে নড়বে, তার সমীকরণ। এবার দড়িটার একটা অংশের কথা ভাবা যাক। দড়ির $l_{1}$ দৈর্ঘ্যের একটি অংশে এই সমীকরণটি কেমন হবে দেখা যাক। যদি এই $l_{1}$ দৈর্ঘ্যের অংশের দুই প্রান্তে যথাক্রমে $T_{1}$ এবং $T_2$ টান অনুভূত হয় তাহলে:

$T_{2} - T_{1}= \frac{ml_{1}}{l}a$

যেখানে $l$ হলো পুরো দড়ির দৈর্ঘ্য। এই সমীকরণটা দেখেই বোঝা যাচ্ছে যে সুতোর বিভিন্ন বিন্দুতে টান বিভিন্ন হবে। সমীকরণটা যে ঠিক সেটা যাচাই করতে সাম্যাবস্থা অর্থাৎ $a= 0$ বসানো যাক। পাওয়া যাবে যে

$T_{1}= T_{2}$

মনে রাখতে হবে যে সুতোটি এখানে অনুভূমিক, তাই ওজনের প্রশ্ন আসে না কারণ মাধ্যাকর্ষণ কাজ করে সুতোটার সাথে উল্লম্বভাবে। অর্থাৎ ত্বরণ না থাকলে দড়ির সর্বত্র টান সমান হওয়াই স্বাভাবিক।

এখানে লক্ষণীয় হল যে $a= 0$ না হলেও $T_{1}= T_{2}$ হবে যদি দড়ি না হয়ে টানাটানির জিনিসটা একটা ভরশূন্য সুতো হয়। এবার কয়েকটি কপিকল (pulley) এর কথা ধরা যাক যারা পরস্পর সুতো দিয়ে যুক্ত। এখানে সুতোটি ভরহীন বলে ধরে নিলে সমস্যাটির সরলীকরণ করা যাবে, যেহেতু এইক্ষেত্রে সুতোর সমস্ত বিন্দুতে টান সমান হবে। এক্ষেত্রে সুতোর নির্দিষ্ট ভর ধরা হলে আগে উল্লেখ করা সমীকরণের মতো একাধিক সমীকরণের সমাধান বের করতে হবে সুতোর প্রান্ত বিন্দুতে টান নির্ণয় করার জন্য।

যাইহোক, যদি সুতোর ভর ব্লক বা কপিকলের ভরের তুলনায় খুব ছোট হয়, তাহলে ভরহীন সুতোর ধারণা এই ধরনের সমস্যাকে সরলীকরণ করে । সরলীকরণ করা সত্ত্বেও যথেষ্ট ভালো সমাধান পাওয়া যায়। অনেক ক্ষেত্রেই আমরা এই ধরনের ধারণা বা assumption প্রয়োগ করি। একটি বাস্তব সমস্যাকে সরল রাখার জন্য এই ধরনের assumption ওই সমস্যার গভীরে পৌঁছাতে সাহায্য করে।

অঙ্ক বাগে আনতে সমস্যার সরলীকরণ করলে কোথায় অসুবিধে হতে পারে

কিন্তু অনেক ক্ষেত্রেই আবার এই ধরনের সরলীকরণের থেকে সঠিক সমাধান পাওয়া যায় না। উদাহরণ হিসাবে বলা যেতে পারে মেকানিক্স-এর অনেক সমস্যার কথা, যেখানে আমরা এমন বস্তুর কথা ধরি যা একেবারে নিখুঁতভাবে কঠিন, অর্থাৎ চাপ পড়লেও যার কোন রকম বিকৃতি হয় না। আসলে যখন এরকম দুটো বস্তু পরস্পরের সংস্পর্শে আসে তখন সবসময়ই কিছুটা বিকৃতি ঘটে। এটা পরিষ্কার ভাবে দেখা যায় যখন কোন ভারী বস্তুকে একটা নরম গদির উপর রাখা হয় বা কোনো ত্বরণ যুক্ত গতিশীল বস্তু মেঝের ওপর চলার সময় বিকৃত হয়। কিন্তু আমরা বিকৃতি ভুলে তর্কের খাতিরে ধরতে পারি যে বস্তুদুটো একটা বিন্দুতে একে অপরের সংস্পর্শে আসছে, এবং সেই সংস্পর্শ বিন্দুতে একজোড়া বল উৎপন্ন হচ্ছে। সেই বলের উৎস নিয়ে মাথা ঘামানোর দরকার নেই।

এই কথাগুলো মাথায় রেখে একটা পরিচিত সমস্যার কথা ধরা যাক। একটা কড়িকাঠ দুই প্রান্তে দুটো অবলম্বনের ওপর রাখা হলো। এখানে কড়িকাঠ, প্রান্তের অবলম্বনগুলো, সবাইকে নিখুঁতভাবে কঠিন ধরা যাক, অর্থাৎ সংস্পর্শ বিন্দুতে বল উৎপন্ন হচ্ছে। যদি কড়িকাঠের ওজন $W$ হয়, অবলম্বন দুটোর প্রতিক্রিয়া সমান এবং বিপরীতমুখী হবে, অর্থাৎ প্রত্যেক অবলম্বনের প্রতিক্রিয়া হবে

$\frac{W}{2}$

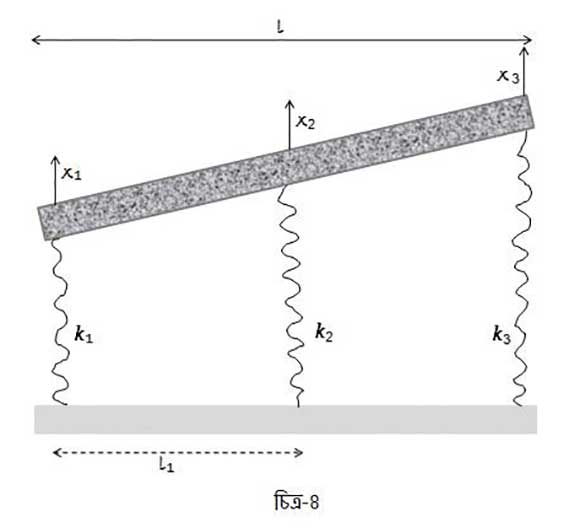
এখন কড়িকাঠের নিচে একেবারে মধ্যিখানে তৃতীয় একটা অবলম্বন রাখা হলো (চিত্র-৩)। কিভাবে তিনটি অবলম্বনের প্রতিক্রিয়া বের করা যাবে?

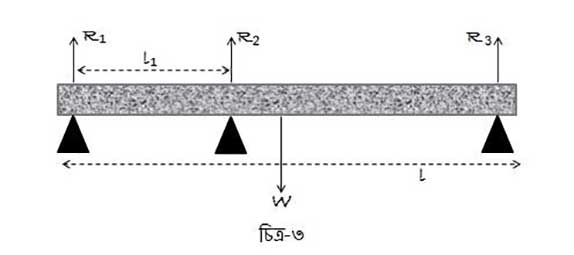
তিনটি অবলম্বনের থেকে প্রতিক্রিয়া ধরা যাক যথাক্রমে $R_{1}$ , $R_2$ এবং $R_3$ । কড়িকাঠের সাম্যাবস্থা বজায় রাখতে হলে তার ওপর কার্যকরী মোট বল এবং টর্ক (torque) শূন্য হবে। বল শূন্য অর্থাৎ ঊর্ধ্বমুখী আর নিম্নমুখী বল সমান:

$R_{1}+ R_{2}+ R_{3}= W$

আর টর্ক শূন্য মানে যেকোনো একটা বিন্দু ধরে মোমেন্ট (moment) বার করলে দু’তরফের মোমেন্ট এক হবে। বাঁদিকের অবলম্বনের ওপর কার্যকরী বলের মোমেন্ট ধরে আমরা লিখতে পারি:

$R_{2}l_{1}+ R_{3}l= \frac{Wl}{2}$

সুতরাং দেখা যাচ্ছে আমাদের কাছে তিনটি অজানা রাশি ( $R_{1}$ , $R_2$ এবং $R_3$ ) আর কেবলমাত্র দুটি সমীকরণ আছে। এখানে লক্ষ্যণীয় যে যদি বলের মোমেন্ট অন্য কোন বিন্দুর পরিপ্রেক্ষিতে ধরা হয় তাহলেও কিন্তু আমরা নতুন কোনো সমীকরণ পাবো না। এর থেকে বলা যায় যে এই সমস্যাটির অসীম সংখ্যক সমাধান হতে পারে।

কেন এই সমস্যার নির্দিষ্ট কোনো সমাধান নেই সেটা বোঝার জন্য আমরা অবলম্বনগুলোর জায়গায় স্প্রিং ব্যবহার করতে পারি (যদিও কড়িকাঠটাকে তখনও কঠিনই ধরছি)। ধরা যাক, এই তিনটি স্প্রিং এর স্প্রিং ধ্রুবক , $k_{1}$ , $k_2$ এবং $k_3$ (নিচের চিত্র-৪) এবং স্প্রিং তিনটে যথাক্রমে $x_{1}$ , $x_2$ এবং $x_3$ সংকুচিত হয়েছে।

তাহলে, আগের দুটো সমীকরণকে লেখা যায়:

$k_{1}x_{1} + k_{2}x_{2} + k_{3}x_{3}= W$

$k_{2}x_{2}l_{1} + k_{3}x_{3}l= \frac{Wl}{2}$

যেহেতু আমরা কড়িকাঠটিকে একটি নিখুঁতভাবে কঠিন বস্তু বলে ধরেছি, সুতরাং আমরা নিম্নলিখিত শর্তগুলি পাব:

$\frac{x_{1} - x_{3}}{l} = \frac{x_{1} - x_{2}}{l_{1}}$

বা:

$(l - l_{1})x_{1} - lx_{2} + l_{1}x_{3} = 0$

আমরা এখন ওপরের সমীকরণগুলিকে সমাধান করতে পারি $x_{1}$ , $x_2$ এবং $x_3$ এর জন্য। ক্র্যামার-এর সূত্র (Cramer’s rule) প্রয়োগ করে পাই:

$x_{1}= \frac{\begin{vmatrix}W&k_{2}&k_{3}\\\frac{W_{1}}{2}&k_{2}l_{1}&k_{3}l\\0&-l&l_{1}\end{vmatrix}}{\begin{vmatrix}k_{1}&k_{2}&k_{3}\\0&k_{2}l_{1}&k_{3}l\\l-l_{1}&-l&l_{1}\end{vmatrix}}$

$x_{2}= \frac{\begin{vmatrix}k_{1}&W&k_{3}\\0&\frac{W_{1}}{2}&k_{3}l\\l-l_{1}&0&l_{1}\end{vmatrix}}{\begin{vmatrix}k_{1}&k_{2}&k_{3}\\0&k_{2}l_{1}&k_{3}l\\l-l_{1}&-l&l_{1}\end{vmatrix}}$

$x_{3}= \frac{\begin{vmatrix}k_{1}&k_{2}&W\\0&k_{2}l_{1}&\frac{Wl}{2}\\l-l_{1}&-l&0\end{vmatrix}}{\begin{vmatrix}k_{1}&k_{2}&k_{3}\\0&k_{2}l_{1}&k_{3}l\\l-l_{1}&-l&l_{1}\end{vmatrix}}$

এই ডিটারমিনেন্টগুলির বিস্তার কষলে আমরা পাব:

$R_{1}= k_{1}x_{1}= \frac{W}{2}\frac{k_{1}k_{3}l^2 - k_{1}k_{2}l_{1}(l-2l_{1})}{k_1k_2l_{1}^2 + k_{1}k_{3}l^2 + k_{2}k_{3}(l-l_{1})^2}$

$R_{2}= k_{2}x_{2}= \frac{W}{2}\frac{k_{1}k_{2}ll_{1} + k_{2}k_{3}l_{1}(l-l_{1})}{k_1k_2l_{1}^2 + k_{1}k_{3}l^2 + k_{2}k_{3}(l-l_{1})^2}$

$R_{3}= k_{3}x_{3}= \frac{W}{2}\frac{k_{1}k_{3}l^2 + k_{2}k_{3}l_{1}(l-l_{1})(l-2l_{1})}{k_1k_2l_{1}^2 + k_{1}k_{3}l^2 + k_{2}k_{3}(l-l_{1})^2}$

উপরের ফর্মুলাগুলো অনেক সহজ হয়ে যায় যদি ধরি

$l_{1}= \frac{l}{2}$

তখন পাই:

$R_1= R_3= W\frac{2k_1k_3}{k_1k_2 + k_2k_3 + 4k_1k_3}$

$R_2 = W\frac{k_1k_2 + k_2k_3}{k_1k_2 + k_2k_3 + 4k_1k_3}$

কঠিন অবলম্বনের ওপর রাখা একটি লম্বা কড়িকাঠের সমস্যাটি বোঝার জন্য আমরা -এর মান সীমিত রেখে $k_i \to \infty$ এবং $x_i \to 0$ এই সীমা পর্যন্ত যেতে পারি (এখানে $i= 1, 2, 3$ )। সরলীকরণের জন্য আমরা $l_1$ কে $\frac{l}{2}$ তেই স্থির এর মধ্যেই সীমাবদ্ধ রাখব।

সমস্ত স্প্রিং গুলি যদি একই ক্ষমতাসম্পন্ন হয় তাহলে আগের সমীকরণ থেকে পাই:

$R_1= R_2= R_3= \frac{W}{3}$

আবার যদি $k_2= k_3$ হয় এবং $k_1$ এর মান $k_2$ বা $k_3$ -এর থেকে অনেকটা বড় হয়, তাহলে:

$\frac{k_2}{k_1}$ বা $\frac{k_3}{k_1}$

যে পদগুলি থাকবে তাদের মান খুব ছোট হওয়ার জন্য সেগুলোকে আমরা বাদ দিতে পারি। সুতরাং:

$R_1= R_3= 2W\frac{k_3}{k_2+4k_3+k_2\frac{k_3}{k_1}}= 2W\frac{k_2}{k_2+4k_2}= \frac{2}{5}W$

$R_2= W\frac{k_2+k_2\frac{k_3}{k_1}}{k_2+4k_3+k_2\frac{k_3}{k_1}}= W\frac{k_2}{k_2+4k_2}= \frac{1}{5}W$

অন্যদিকে আবার যদি $k_1= k_3$ হয় এবং $k_2$ এর মান $k_1$ বা $k_3$ এর থেকে অনেকটা বড় হয়, তাহলে আমরা পাব:

$R_1= R_3= 2W\frac{k_1\frac{k_3}{k_2}}{k_1+k_3+4k_1\frac{k_3}{k_2}}= 0$

$R_2= W\frac{k_1+k_3}{k_1+k_3+4k_1\frac{k_3}{k_2}}= W$

এর মানে হল, যদি মাঝের স্প্রিংটি প্রান্তস্থ দুটি দুই স্প্রিং-এর থেকে অনেকটা বেশী শক্তিশালী হয়, তাহলে প্রান্তস্থ স্প্রিংগুলির কার্যত কোন ভুমিকা থাকেনা। এখানে লক্ষ্যণীয় যে সমস্ত সমাধানই ওপরের বল ও টর্ক এর সমীকরণগুলি মেনে চলে।

অর্থাৎ একেকটা অবলম্বন কতটা ওজন বইছে, সেটা নির্ভর করছে কিভাবে আমরা

$k_i \to \infty$ এবং $x_i \to 0$ সীমার দিকে যাচ্ছি, তার ওপর। কোনো একটা নির্দিষ্ট উত্তর নেই। সমস্যাটাকে সহজ করতে কড়িকাঠ অবলম্বন উভয়কেই কঠিন বস্তু হিসেবে ধরা যায় কিন্তু সেটা করলে আর কোনো সমাধানই পাওয়া যায়না। আসলে ইঞ্জিনিয়ারদের থামের উপর কড়িকাঠ বানানোর সময় থামের প্রতিক্রিয়ার একটা আন্দাজ দিতে হয়। এটা করার সময় তারা কিন্তু কড়িকাঠ থাম কাউকেই একেবারে নিখুঁতভাবে কঠিন ধরে না।

প্রচ্ছদ ও অন্যান্য ছবি: বনানী মণ্ডল

(এই লেখাটি মূল ইংরাজি থেকে বাংলায় অনুবাদ করেছে ‘বিজ্ঞান’ টীম-এর ঝুমা সন্নিগ্রাহী আর অনির্বাণ গঙ্গোপাধ্যায়।)

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.