04-03-2026 23:16:16 pm
বিজ্ঞান - Bigyan
বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine
https://bigyan.org.in
ক্যাওসেও সমলয়ন!
Link: https://bigyan.org.in/synchronization-in-chaos

গোপন সংকেত পাঠানো এবং আড়ি পেতে সেই সংকেত পড়ে ফেলা, দ্বিতীয় বিশ্বযুদ্ধের বোমাবাজির আড়ালে চলছিল আরেক যুদ্ধ। কে তাদের গোপন সংকেতকে কতটা সুরক্ষিত করতে পারে আর কে শত্রুর সংকেত-এর সুরক্ষাকে ভাঙতে পারে, সেই লড়াই চলছিল মিত্রশক্তি (ব্রিটেন, আমেরিকা) আর অক্ষশক্তির (জার্মানি, জাপান) মধ্যে। সেই যুদ্ধে যে জিতবে, বোমাবাজির যুদ্ধেও এগিয়ে সে। শত্রু কোথায় হামলা করবে, আগে থাকতে জেনে যাচ্ছে যে!
কিন্তু সেই সংকেতকে যদি এমন সুরক্ষা দেওয়া যেতো যে যাকে পাঠানো হচ্ছে, তার বাইরে আর কেউ সেটা পড়তে পারবে না, তাহলে কেমন হতো? তখন নিশ্চিন্ত হওয়া যেতো যে গোপন সংকেত গোপনই থাকছে। এই সংকেত গোপন রাখার অনেক ফিকির বেরিয়েছে। এর মধ্যে একটা হলো সংকেতটাকে একটা ক্যাওটিক (chaotic) সিগনালের মধ্যে লুকিয়ে রাখা।
সংকেত গোপন রাখার অনেক ফিকির বেরিয়েছে। এর মধ্যে একটা হলো সংকেতটাকে একটা ক্যাওটিক (chaotic) সিগনালের মধ্যে লুকিয়ে রাখা।
ক্যাওস (chaos)
স্কুলে পদার্থবিদ্যার ক্লাসে আমরা যেসব সিস্টেম দেখি, (যেমন- সরল পেন্ডুলাম) তাদের ক্ষেত্রে প্রাথমিক অবস্থার সামান্য পরিবর্তন হলে চলপথেরও সামান্যই পরিবর্তন ঘটে।
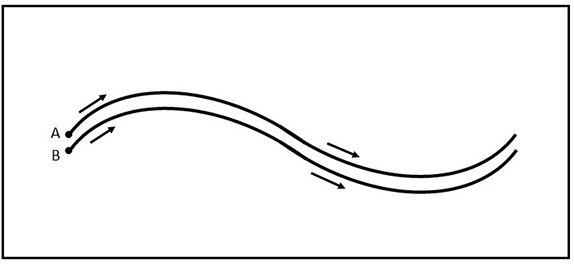
(A থেকে B) চলপথেরও সামান্যই পরিবর্তন ঘটছে।
কিন্তু ক্যাওটিক সিস্টেমে এটা খাটে না। সেক্ষেত্রে প্রাথমিক অবস্থার সামান্য পরিবর্তন করলেই চলপথের চেহারা পুরোপুরি বদলে যেতে পারে।
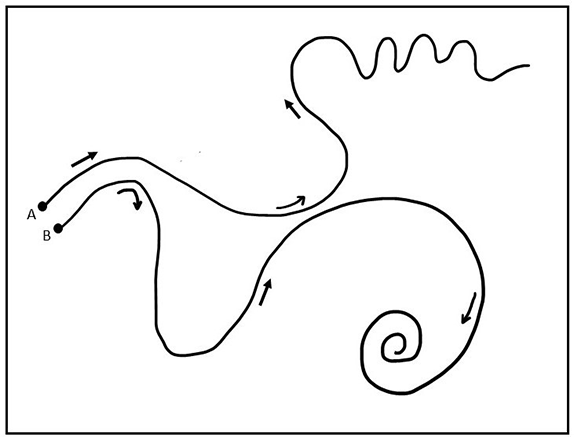
(A থেকে B) চলপথের চেহারা পুরোপুরি বদলে যাচ্ছে।
যে কোনো একটা ক্যাওটিক চলপথ লক্ষ্য করলেও একটা অদ্ভুত জিনিস নজরে পড়বে। তার চলার কোনো মাথামুন্ডু নেই। হঠাৎ কোথায় কখন বাঁক নেবে কি চরকিপাক ঘুরবে বলা অসম্ভব।
বিজ্ঞানীরা অঙ্ক কষে দেখিয়েছেন যে দুটো ক্যাওটিক সিস্টেমের মধ্যে যদি আন্তঃক্রিয়া থাকে তাহলে অনেক সময় তারা বেশ আলাদা আলাদা অবস্থা থেকে শুরু করলেও একটু পর একই তালে চলতে থাকে।
সমলয়ন
সমলয়ন হলো এমন একটা ব্যাপার যেখানে অনেকগুলো সিস্টেম আলাদা আলাদা অবস্থা থেকে শুরু করলেও একটু পর সবাই একই ছন্দে বাঁধা পড়ে যায়। এইটা সম্ভব হওয়ার জন্যে সিস্টেমগুলোর মধ্যে আন্তঃক্রিয়া (interaction) থাকা জরুরি।
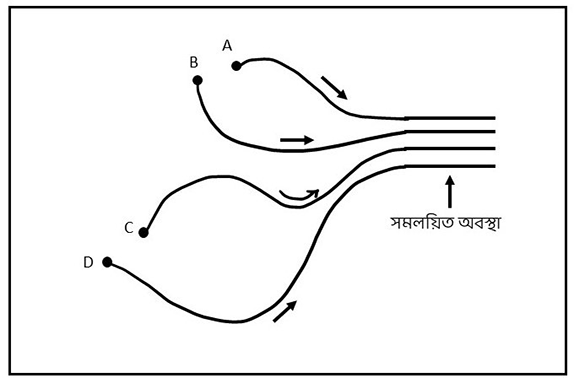
শুরু করলেও (A, B, C, এবং D) একটু পর সবাই একই ছন্দে বাঁধা পড়ে যাচ্ছে।
সমলয়িত ক্যাওস
ওপরের ছবিগুলো দেখে মনে হবে ক্যাওস আর সমলয়ন দুটো পরস্পর বিরোধী জিনিস। ক্যাওসে দুটো সিস্টেম কিছুতেই একসাথে চলতে চায় না, শুরুর অবস্থার একটু হেরফের হলেই একে অন্যের থেকে একদম আলাদাভাবে চলতে থাকে। অন্যদিকে সবাই মিলে এক তালে চলারই আরেক নাম হলো সমলয়ন। কিন্তু বিজ্ঞানীরা অঙ্ক কষে দেখিয়েছেন যে দুটো ক্যাওটিক সিস্টেমের মধ্যে যদি আন্তঃক্রিয়া থাকে তাহলে অনেক সময় তারা বেশ আলাদা আলাদা অবস্থা থেকে শুরু করলেও একটু পর একই তালে চলতে থাকে। এই চলাটা আগের মতোই মাথামুন্ডুহীন ক্যাওটিক পথেই হয়, কিন্তু দুটো সিস্টেমই একই ক্যাওটিক পথে চলতে থাকে। অর্থাৎ ক্যাওস আর সমলয়নের মেলবন্ধন ঘটে [1]।
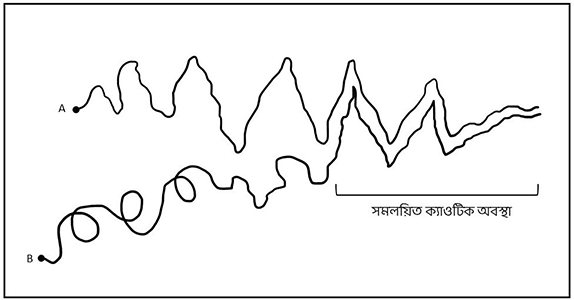
শুরু করলেও (A আর B) শেষমেষ একই তালে কিন্তু ক্যাওটিক পথে চলছে।
এইসব করে লাভ কী ?
আপাত দৃষ্টিতে তোমাদের মনে হতেই পারে এইরকম ভীষণ তাত্ত্বিক গবেষণা আমাদের দৈনন্দিন জীবনে কোনো কাজে লাগে না। এসব তাত্ত্বিক গবেষণা বিজ্ঞানীদের আকাশকুসুম মাত্র। কিন্তু এই ক্যাওস এবং সমলয়ন মেলবন্ধনের অসাধারণ এক প্রয়োগও বিজ্ঞানীরা ভেবে বার করেছেন [2]।
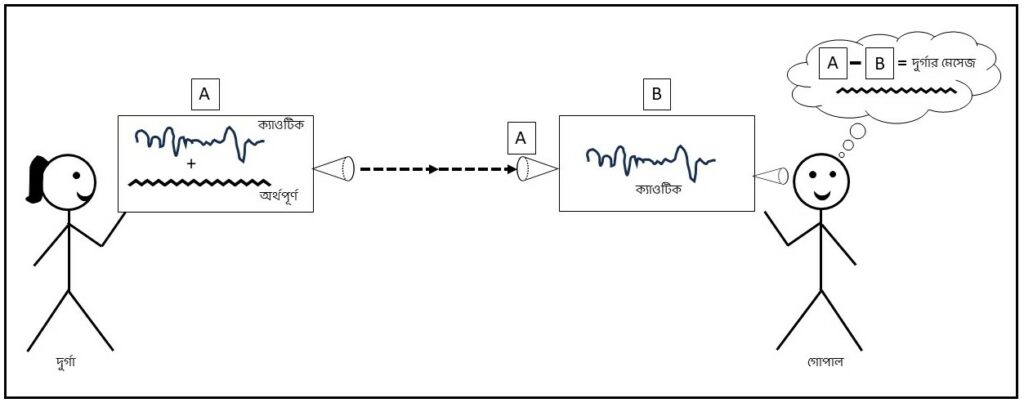
প্রয়োগটা বুঝতে সুবিধা হবে যদি ধরো A আর B আসলে দুটো বস্তুকণা নয়, বরং দুটো লেজার রশ্মি। আর ছবিতে দুটো বস্তুর চলপথ নয়, বরং সময়ের সাথে সাথে ওই লেজার দুটোর তীব্রতার পরিবর্তনকে দেখাচ্ছে (X-অক্ষ: সময়, Y-অক্ষ: রশ্মির তীব্রতা)। অর্থাৎ লেজার দুটোর তীব্রতা সময়ের সাথে ক্যাওটিক ভাবে বাড়ছে-কমছে। আরও ভাবো A লেজার যন্ত্রটা দুর্গার হাতে ধরা আছে যা থেকে সে রশ্মি পাঠাচ্ছে অনেক দূরে বসা গোপালকে। গোপালের হাতে ধরা রয়েছে B লেজার যন্ত্র। B-যন্ত্রের ওপর A-রশ্মি পড়ে তাকে উত্তেজিত করছে যার ফলে তার থেকে নিজস্ব B-রশ্মি বেরোচ্ছে। এবং সমলয়নটা ঘটছে এইভাবে দুটো রশ্মির আন্তঃক্রিয়ার ফলে। অর্থাৎ শুরুর একটু সময় পর থেকে A-রশ্মি আর B-রশ্মির তীব্রতা সমান তালে কিন্তু ক্যাওটিকভাবে ওঠা নামা করছে।
এইবার মনে করো দুর্গা গোপালকে একটা গোপন সংকেত পাঠাতে চায় তার A লেজার রশ্মির মাধ্যমে। ধরো সে খুব সহজেই A-রশ্মির ক্যাওটিক ওঠা নামার সাথে আরও একটু-আধটু পরিবর্তন জুড়ে দিতে পারে। অর্থাৎ মূল ক্যাওটিক রশ্মির সাথে কম তীব্রতাসম্পন্ন সাধারণ (অর্থাৎ ক্যাওটিক নয়) একটা আলোকতরঙ্গের উপরিপাত (superposition) ঘটিয়ে দিতে পারে। এই ক্যাওটিক নয় যে পরিবর্তনটুকু সেইটার মধ্যেই দুর্গার গোপন সংকেতটা আছে।
এই অর্থপূর্ণ সংকেতটুকু তৃতীয় কোনো লোকের পক্ষে জানা অসম্ভব কারণ ওই সামান্য পরিবর্তনগুলো বিদঘুটে মাথামুন্ডুহীন ক্যাওটিক সংকেতের সাথে মিশিয়ে আছে। কিন্তু গোপালের কথা আলাদা। তার নিজের B-রশ্মি সমলয়নের কারণে A-রশ্মির ক্যাওটিক অংশটুকুর সাথে তাল মিলিয়ে চলছে। মজাটা হলো A-রশ্মিতে দুর্গার ওই ইচ্ছাকৃত একটু-আধটু নন-ক্যাওটিক পরিবর্তনগুলো কিন্তু B-রশ্মির সাথে সমলয়িত হয় না, খালি ক্যাওটিক অংশটুকুই হয়। এইটা বিজ্ঞানীরা অঙ্ক কষে প্রমাণ করেছেন। সুতরাং গোপাল দুর্গার থেকে আসা A-রশ্মির থেকে নিজের হাতে থাকা B-রশ্মি বিয়োগ করলেই দুর্গার ওই ইচ্ছাকৃত একটু-আধটু পরিবর্তনগুলো ধরে ফেলবে। অর্থাৎ দুর্গার পাঠানো গোপন সংকেত বুঝে যাবে!
ক্যাওটিক সংকেতের সাথে অর্থপূর্ণ সংকেত মিশিয়ে এইভাবে গোপন তথ্য আদানপ্রদানের উপায়টা বছর তিরিশ আগে বিজ্ঞানীরা তাত্ত্বিক ভাবে ভেবেছিলেন। ল্যাবরেটরিতে কয়েকটা ছোট পরীক্ষা করেও এটা যাচাই করা হয়েছিল। কিন্তু 2005 সালে গ্রিসের এথেন্স শহরে একদল বিজ্ঞানী অপটিক্যাল ফাইবার আর লেজার রশ্মি ব্যবহার করে 120 কিলোমিটার দূরে গোপন তথ্য আদানপ্রদানে সক্ষম হয়েছেন [3] !
সুতরাং বুঝতেই পারছো অদূর ভবিষ্যতে হয়তো তোমার ব্যাঙ্কের জমা-খরচের হিসেব বা ইমেল -এর মেসেজের গোপনীয়তা রক্ষা করা যায় ক্যাওস আর সমলয়নের মেলবন্ধনের মাধ্যমেই।
(প্রচ্ছদের ছবির সূত্র: Nature )
রেফারেন্স:
[1] Pecora, L. M. & Carroll, T. L., Synchronization in chaotic systems. Phys. Rev. Lett. 64, 821 (1990)
[4] Roy, R. Chaos down the line. Nature 438, 298 (2005)
লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।
Scan the above code to read the post online.
Link: https://bigyan.org.in/synchronization-in-chaos
