07-03-2026 01:59:19 am
বিজ্ঞান - Bigyan
বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine
https://bigyan.org.in
বৃষ্টির মধ্যে পড়লে কি ছোটা উচিত?
Link: https://bigyan.org.in/should-we-run-in-rain

বৃষ্টির মধ্যে ভূপতি
ভূপতি গ্রামের হাইস্কুলে পড়ে। এবারে উচ্চমাধ্যমিক দেবে। পদার্থবিদ্যা ওর খুব ভালো লাগে। এ-বিষয়টা পড়ান সুলতানা দিদিমণি। পই পই করে ছাত্রদের তিনি বলেন, চারপাশে যা কিছু ঘটতে দেখছো, সেগুলোকে ক্লাসে শেখানো পদার্থবিদ্যার সূত্রগুলো দিয়ে ব্যাখ্যা করার চেষ্টা করো। এতে দারুণ মজা পাবে। আগে নিজে চেষ্টা করে দেখো। না পারলে আমি তো রয়েইছি। কেন জানি না দিদিমণির উপদেশটা ভূপতির খুব মনে ধরলো।
একদিন স্কুল ছুটির পর ভূপতি বাড়ির দিকে হাঁটা দিয়েছে। একটু যেতেই হঠাৎ দেখলো আকাশ জুড়ে ঘন কালো মেঘ। যাঃ! ছাতা নিতেও গেছে ভুলে। ঝমঝম করে নামলো বৃষ্টি। পুরো কাকভেজা হয়ে বাড়ি ফিরতে হলো। ওদের পাশেই চারুদের বাড়ি। সেও ভূপতির সঙ্গে পড়ে। একসাথেই ছুটি হয়েছে। কিছুক্ষণ আগে ফিরেছে সেও। তারও নিশ্চয় একই অবস্থা, ভূপতি ভাবলো।
জিজ্ঞেস করতে চারু বললো, কই! তোর মতো অমন ভিজিনি বাপু। আসলে আমার সাইকেল ছিলো তো, তাই রক্ষে। বৃষ্টি শুরু হতেই জোরে প্যাডেল করে সোজা ঘর। নাহলে অবস্থা কাহিল হতো।
রাতে পড়তে বসে ব্যাপারটা নিয়ে ভাবতে লাগলো ভূপতি। কীভাবে ব্যাখ্যা করা যায় ঘটনাটাকে? ও আর চারু দু-জনেই বৃষ্টির মধ্যে প্রায় একই পথ এসেছে। খালি তফাৎটা হচ্ছে চারু এসছে সাইকেল চড়ে আর ও হেঁটে। তাই, চারু ওর থেকে অনেক তাড়াতাড়ি বাড়ি পৌঁছেছে। মানে ওর ওপর চারুর তুলনায় খানিকটা বেশি সময় ধরে বৃষ্টি পড়েছে। স্বাভাবিক, ও তো বেশি ভিজবেই। এই সব সাত-পাঁচ ভাবতে ভাবতে ঘুমিয়ে পড়লো ভূপতি।
বৃষ্টি কোনদিকে পড়ে?
পরদিন আবার স্কুল। প্রথম পিরিয়ডে সুলতানা দিদিমণির ক্লাস। উনি এখন ভেক্টর পড়াচ্ছেন। গতিবেগ যে ভেক্টর সেটা মানতে ওর একটুও অস্বস্তি হলো না। এর মান আছে, সঙ্গে দিশাও। কিন্তু, খটকা লাগলো যখন দিদিমণি ভেক্টরের উদাহরণ দিতে গিয়ে ক্ষেত্রফলের প্রসঙ্গ টানলেন। জ্যামিতি ক্লাসে ভূপতি বিভিন্ন সুষম জিনিসের ক্ষেত্রফলের মান বার করার সূত্র শিখেছে। কিন্তু তার দিশা জানার কী রীতি?
সুলতানা বললেন, তোমাদের অঙ্ক খাতার একটা পাতা ছিঁড়ে সেটাকে একদম টানটান করে ধরো। এটাকে এখন সমতল ভাবতে পারি। এর দুটো দিকই খোলা। সুন্দর একটা সীমানা আছে যার দৈর্ঘ্য বা প্রস্থ কোনোটারই মান অসীম নয়। কারণ সীমানাটা বদ্ধ (closed)। এবার মনে করো ঐ সীমানা ধরে ডান পাকের একটা screw ঘোরানো হচ্ছে।[1] তাহলে তার মাথাটা কোন দিকে এগোবে? ঠিক পাতার সাথে লম্ব বরাবর নয় কি? হ্যাঁ, ওটাই হলো পাতাটার ক্ষেত্রফলের দিশা।
এবার আর ভূপতির মনে কোনো ধন্দ রইলো না।
পরদিন ক্লাসে সুলতানা বললেন, মনে করো, চারু নিজের বেঞ্চে ঠায় বসে আছে। এই অবস্থায় সে জানলা দিয়ে দেখলো বৃষ্টির জলের ফোঁটাগুলো আকাশ থেকে একদম খাড়াভাবে মাটিতে পড়ছে। মনে করো তার সাপেক্ষে ফোঁটাগুলোর গতিবেগ ।
ভূপতি জিজ্ঞেস করলো, আচ্ছা দিদিমণি, এটা কি সত্যি সম্ভব? বর্ষাকালে তো দেখেছি প্রায় সবসময় কমবেশি হাওয়া চলে। তখন তো মাটিতে দাঁড়িয়ে স্পষ্ট বোঝা যায় জলের ফোঁটাগুলো খাড়া ভাবে পড়ছে না। হাওয়ার দিক অনুযায়ী এঁকেবেঁকে যাচ্ছে। তাহলে?
সুলতানা বললেন, হ্যাঁ, সে তো বটেই। শুরুতে অত জটিলতার মধ্যে ঢুকতে চাইছি না।
ভুপতি শুধোলো, দিদিমণি, বৃষ্টির সময় সব জলের ফোঁটার গতি কি একই হয়? কেন?
সুলতানা বললেন, মোটেই না। মাটিতে পড়ার সময় কোন ফোঁটার গতি কতটা হবে, সেটা নির্ভর করে তার আকারের ওপর। যত বড় আকারের ফোঁটা, তার গতিও তত বেশি। আরও কয়েকটা জিনিসের ওপর এই গতি নির্ভর করে। কিন্তু সেটা অন্য আলোচনা।
এখন মনে করো চারুর সাপেক্ষে ভূপতি বৃষ্টির মধ্যে স্রেফ দাঁড়িয়ে আছে। তাহলে সে-ও জলের ফোঁটাগুলো একই বেগে পড়তে দেখে। তাই বৃষ্টিতে ওর শুধু মাথাটুকু ভিজবে, বড়জোর কাঁধ। শরীরের আর কোনো অংশ ভিজবে না। কিন্তু যদি মনে করো চারু দেখলো ভূপতি ঐ বৃষ্টির মধ্যে বেগে সাইকেল চালিয়ে যাচ্ছে। তাহলে, ভূপতির সাপেক্ষে জলের ফোঁটার গতিবেগ আগের মতো হবে না। কি হবে?
এই বলে সুলতানা বোর্ডে লিখলেন:
সাথে সাথে বললেন, এটাই হচ্ছে আপেক্ষিক বেগ বার করার নিয়ম। মনে রাখবে, ভেক্টরগুলোর মধ্যে যোগ-বিয়োগ কিন্তু বীজগণিতের চেনা নিয়মে হয় না। এরপর তিনি বোর্ডে সুন্দরভাবে অঙ্ক করে দেখিয়ে দিলেন -এর মান আর দিশা বার করার সূত্র হলো:
এরপর তিনি বোর্ডে এই ছবিটা আঁকলেন।
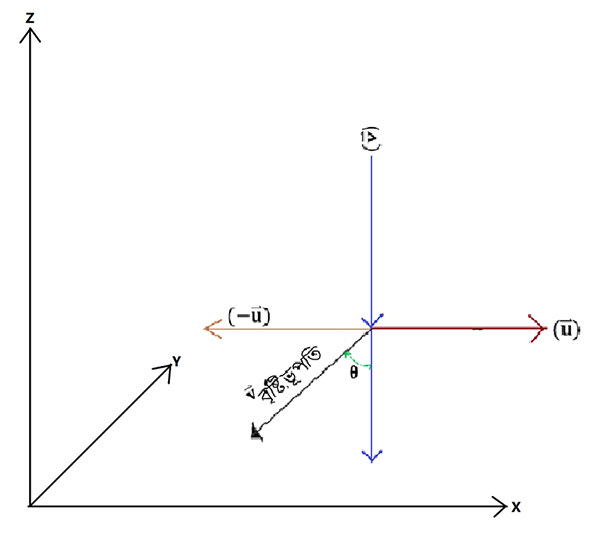
সেই সাথে বলে চললেন, এখন অঙ্ক কষার সুবিধের জন্য একটা ত্রিমাত্রিক কার্তেসীয় নির্দেশতন্ত্র (3D Cartesian Reference Frame) নেওয়া যাক। মনে মনে ভেবে নাও, চারুর সাপেক্ষে ভূপতি এই নির্দেশতন্ত্রের -অক্ষের পজিটিভ দিকে যাচ্ছে আর জলের ফোঁটাগুলো পড়ছে
-অক্ষের নেগেটিভ দিকে। তাহলে,
কে দুটো উপাংশে ভাগ করে নেওয়া যায়। এর অনুভূমিক উপাংশ
আর উলম্ব উপাংশ
একটু থেমে সুলতানা বললেন, আজ বাড়ি গিয়ে চট করে একটা অঙ্ক কষে ফেলো তো। মনে করো, চারু মাপলো -এর মান সেকেন্ডে 8 m/s। ঠিক আছে? খুব আস্তে আস্তে হেঁটে গেলে সচরাচর
হয় 1 m/s। আর সাইকেল নিলে হয় 10 m/s। কেমন? এবার, এই দুই ক্ষেত্রে অঙ্ক কষে বার করো দেখি ভূপতির সাপেক্ষে জলের ফোঁটার দিশা কী হবে?
সন্ধেবেলা ভূপতি অঙ্কটা নিয়ে বসলো। কঠিন কিছু নয়। সূত্রটা আজই দিদিমণি বলে দিয়েছেন। এখন একটু ত্রিকোণমিতি ঘাঁটলেই হবে। ও বার করলো হাঁটার সময় জলের ফোঁটা ঠিক খাড়া ভাবে না, খুব সামান্য (প্রায় ) হেলে পড়ে। তাই মোটামুটিভাবে বৃষ্টির মধ্যে দাঁড়িয়ে থাকা আর আস্তে হেঁটে যাওয়ার মধ্যে বড় ফারাক নেই।
কিন্তু সাইকেলে গেলে জলের ফোঁটা আগের চেয়ে অনেক বেশি () তেরচা ভাবে পড়ে।
পরদিন সুলতানা প্রিয় ছাত্রের থেকে উত্তরটা পেয়ে খুব খুশি হলেন। বললেন, বুঝতেই পারছো যত বেশি হয়, জলের ফোঁটাগুলো তত তেরচা ভাবে তোমার ওপর পড়ে।
বৃষ্টিতে হাঁটবো না ছুটবো?
রাতে ভূপতি আজকের পড়ার সাথে দিন কয়েক আগে বৃষ্টিতে ভেজার ঘটনাটা নিয়ে আবার চিন্তা করতে লাগলো। মোদ্দা কথা হচ্ছে বৃষ্টির মধ্যে ধীরে ধীরে হেঁটে এলে শরীরে বেশি জলের ফোঁটা লাগে বটে। কিন্তু শুধু উপরটা ভেজে। আর সাইকেল চড়ে এলে জল যতই কম লাগুক, মাথা তো ভেজেই, সঙ্গে নাক-মুখ সহ শরীরের সামনের অংশটাতেও জলের ঝাপটা লাগে। কোনটা কী পরিমাণে ভিজবে সেটা যদিও নির্ভর করে ওর শরীরের কোন অংশের কী রকম মাপ আর জল কতটা গায়ে লাগছে তার ওপর। যাই হোক, মাথা আর কতটুকু? সামনের অংশটা তো অনেকখানি জায়গা। তাহলে লাভ কীসে? হেঁটে না ছুটে? ধুর ছাই! কিছুই বুঝতে পারছে না ও। আজকের ক্লাস করে কেমন যেন সব গুলিয়ে গেছে। নাহ, কাল দিদিমণিকে আবার ধরতে হবে, ভূপতি ভাবলো।
পরদিন টিফিনের সময় সুলতানাকে পাওয়া গেলো। ভূপতি তার সমস্যাটা খুলে বলতে সুলতানা তো দারুণ উত্তেজিত।
তিনি বললেন, একটা কায়দা শিখিয়ে দিচ্ছি। তাত্ত্বিক ভাবে কোনো বাস্তব সমস্যার মীমাংসা করতে এটা সবসময় কাজে লাগবে। গোড়াতে, সমস্যাটার কাছাকাছি একটা গাণিতিক মডেল ধরে নিতে হয়। এর মধ্যে কেবলমাত্র সমস্যাটার সবচেয়ে গুরুত্বপূর্ণ বিষয়গুলো বলা থাকে। বাকিগুলো আসল সমস্যাটার ওপর উপযুক্ত কিছু শর্ত চাপিয়ে ছেঁটে ফেলা হয়। ফলে মডেলটা অনেক সরল হয়। এরপর সেটা দিয়ে অঙ্ক কষে পাওয়া ফলাফল থেকে হরে-দরে একটা ধারণা গড়ে তোলার চেষ্টা করা হয়। যদি সেটা সত্যি পারা যায়, তাহলে ধাপে ধাপে শুরুর মডেলের ওপর চাপানো শর্তগুলোকে সরিয়ে রেখে আসল সমস্যাটার দিকে এগোতে হয়। এতে মডেলটা আরও উন্নত, বেশি কাজের হয়ে ওঠে। তোমাকেও তাই করতে হবে।
মনে মনে ভাবো, মাটিতে দাঁড়িয়ে চারু দেখছে — গোটা রাস্তা জুড়ে এমনভাবে বৃষ্টি হচ্ছে যাতে যেকোনো জায়গায় একটা বাটি বসিয়ে দিলে নির্দিষ্ট সময় পর তাতে একই পরিমাণ জল জমা হয়। সবকটা জলের ফোঁটা পড়ছে একদম খাড়াভাবে। আর তাদের গতি একই। শুধু তাই নয়, সময়ের সঙ্গে তা পাল্টাচ্ছে না।
একটু দম নিয়ে সুলতানা বললেন, এবার কল্পনা করো তুমি যে রাস্তা দিয়ে যাচ্ছো, সেটা এক্কেবারে সোজা। তাতে কোনো বাঁক নেই। আর সেটা দারুণ মসৃণ। কোনো খানা-খন্দের বালাই নেই।
অবাক হয়ে ভূপতি জিজ্ঞেস করলো, বলেন কী? দুনিয়ায় কোনো রাস্তা এমন আছে?
উত্তরে সুলতানা বললেন, নেই জানি। কিন্তু ভাবতে তো দোষ নেই।
ভূপতি বললো, আচ্ছা। কিন্তু রাস্তা টেরাবাঁকা হলে কি অঙ্কটা করা যাবে না?
সুলতানা বললেন, যাবে না তো বলিনি। অবশ্যই যাবে। তখন ওই বাঁকা রাস্তাটাকে অনেকগুলো টুকরো টুকরো সোজা রাস্তাতে ভেঙে নিতে হবে। জ্যামিতিতে পড়োনি যে বৃত্তের চাপকে অনেক গুলো ছোট ছোট সরলরেখার অংশ হিসেবে দেখা হয়? সেরকম। তবে আপাতত ব্যাপারটাকে অত জটিল করতে চাইছি না। এবার আমার একটা প্রশ্ন আছে। ভেক্টর ক্ষেত্র কাকে বলে জানো?
ভূপতি বললো, হ্যাঁ, আপনিই তো পড়িয়েছেন — মহাকর্ষ ক্ষেত্র, তড়িৎ ক্ষেত্র, চৌম্বক ক্ষেত্র। বিশেষ একটা ভেক্টর ক্ষেত্রের মধ্যে থাকা কোনো অঞ্চলের প্রতিটা বিন্দুতে ঐ ভেক্টরটার মান এবং দিশা বার করা যায়।
সুলতানা খুব সন্তুষ্ট হলেন। বললেন, ঠিক, এবার তবে আসল আলোচনায় ফেরা যাক। এই অঙ্কটা কষতে হলে তোমাকে নতুন একটা ভেক্টর ক্ষেত্র নিতে হবে। বুঝলে? ‘বৃষ্টি-ক্ষেত্র’। আগে কাগজ-কলম নিয়ে এসো তো। মুখে মুখে এসব হয়? সেটা দিতে তিনি বললেন, মনে করো, এই ক্ষেত্রের প্রতিটা বিন্দুতে বৃষ্টি-ঘনত্ব() আছে। এর সংজ্ঞা দিতে পারো:
ভূপতি জিজ্ঞেস করলো, টা কী? জলের ঘনত্ব?
সুলতানা বললেন, আরে না। এর মানে হলো প্রতি সেকেন্ডে বাতাসের প্রতি ঘনমিটারে কত kg বৃষ্টির জল রয়েছে। আপাতত: এর মান 1 ধরে নাও। কোনো অসুবিধে নেই। তাহলে, আমাদের ধরে নেওয়া শর্ত অনুযায়ী ভেক্টর ক্ষেত্রটা সুষম এবং সময়ের সঙ্গে এর কোনো পরিবর্তন হচ্ছে না। এখন দেখো, একেও উপাংশে ভাগ করা যায়।
,
এবং
তাই না? বেশ, এই ভেক্টর ক্ষেত্রটায় রাখা কোনো মুক্ত তলের মধ্য দিয়ে -এর Flux মাপতে হবে। পারবে তো? এর জন্য শুধু জানতে হবে ওই তলের ক্ষেত্রফলের দিশা বরাবর
-এর উপাংশটা কী? তার সাথে ক্ষেত্রফলের মান পাতি গুণ করে দিলেই Flux পাওয়া যায়[টীকা]। তাহলে, যাওয়ার সময় তোমার শরীরের যে তলগুলো ভিজেছে, তার মধ্য দিয়ে
-এর Flux (
) বার করে ফেলো।
কি হে? ঘাবড়ে গেলে যে? তোমাদের যে ইতিমধ্যে পড়ালাম ভেজা তল কোন-কোনটা হবে?
ভূপতি বললো, সেটা নিয়ে ভাবছি না। জ্যামিতির বইতে এরম তলের ক্ষেত্রফল মাপার কোনো ধরা-বাঁধা সূত্র তো পড়িনি।
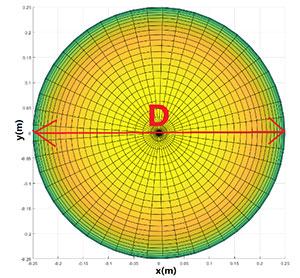
একটু গম্ভীর গলায় সুলতানা বললেন, হুম, তা ঠিক। মানুষের শরীরের গঠন বেশ জটিল। সেইজন্য আবার একটা জিনিস কল্পনা করতে হবে। ধরে নাও, তোমার শরীরের জ্যামিতিটা অনেকটা লম্ব বৃত্তাকার চোঙের মত। একে -এর পজিটিভ দিকে খাড়া করে মাটিতে বসিয়েছো। তোমায় শুধু ধরে নিতে হবে চোঙটা এত শক্ত যে এক জায়গা থেকে অন্য জায়গায় সরলে মোটেই মচকায় না।
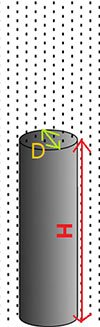
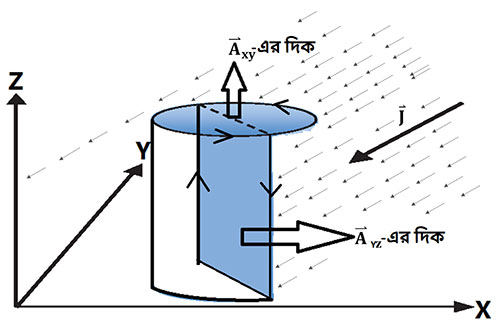
এবার ভূপতি একটু বিরক্ত হলো। বললো, আর পারছি না। সাইকেল চালানোর সময় কি তাই হয়? প্যাডেল করলে শরীর তো বেঁকবেই। তার গড়নও পাল্টাবে। সুলতানা ওকে সান্ত্বনা দিয়ে বললেন, রাগ করো না। বলছি না শুরুটা করতে হয় সহজ ভাবে। এতে ভেজা তল দুটোর ক্ষেত্রফল বার করতে দারুণ সুবিধা হবে। কী রকম? তোমার মাথায় কতটা জায়গা জুড়ে জল পড়ছে, সেটা মাপতে চাইলে তুমি চোঙের ওপরের ভূমির ক্ষেত্রফলটা (ধরে নাও, ) নেবে। চোঙের ব্যাস (
) জানলেই এটা বেরিয়ে আসবে। আর সামনের দিকে কতটা জায়গা ভিজেছে জানতে হলে একটা কাজ করতে পারো। চোঙটার মাঝখানে
বরাবর আড়াআড়ি কেটে ফেললে একটা আয়তাকার অংশ পাওয়া যায়। চোঙের উচ্চতা (
) হচ্ছে ঐ আয়তক্ষেত্রের দৈর্ঘ্য আর
হলো প্রস্থ। এর ক্ষেত্রফলটা (ধরে নাও,
) বার করলেই কাজ হয়ে যাবে। আর দিশা কেমন হবে সে তো আগের ক্লাসে বলে দিয়েছি। একটু খুঁটিয়ে দেখো
এবং
-এর দিশা হবে যথা:
ও
অক্ষের +ve দিক বরাবর।
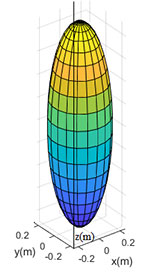
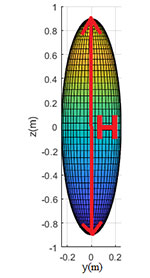
ভূপতি বললো, দিদিমণি, মানুষের শরীর কি চোঙের মত? আটপৌরে জিনিস গুলোর সঙ্গে যদি তুলনা টানতে বলেন, তাহলে কতকটা পটলের মতো বলা যায়।
সুলতানা বললেন, হ্যাঁ, সেরমও নিতে পারো। জ্যামিতিতে একে বলে Ellipsoid। তাহলে বলো এক্ষেত্রে ,
কত হবে?
পারলে না তো। প্রথমে এটাকে বরাবর দেখো। কার মতো দেখাচ্ছে? ভূপতি মাথা চুলকে বললো, বৃত্তের মত। ও বুঝেছি, তাহলে
সুলতানা বললেন, ঠিক। ওই আগের চোঙটার মতই। এবার Ellipsoid-টাকে -বরাবর দেখো। কেমন লাগছে?
ভূপতি বললো, এতো উপবৃত্ত (Ellipse)। দাঁড়ান, তার মানে
সুলতানা বললেন, বাঃ, আর তক্কো না বাড়িয়ে অঙ্কটা কষে ফেলো গিয়ে। প্রথমে তুমি তোমার মাথার তলের মধ্যে দিয়ে -এর Flux (
) কীভাবে বার করবে দেখাও। একটু চিন্তা করে ভূপতি খাতায় লিখলো,
সুলতানা গদগদ হয়ে বললেন, একদম ঠিক লিখেছো। এই তলের দিশা বরাবর -এর উপাংশ হচ্ছে
। ঘুরিয়ে বলা যেতে পারে, এই তলে শুধুমাত্র
-এর জন্য flux থাকে। এখন
আর
-এর মানটা সমীকরণে বসিয়ে তুমি লিখতেই পারো
তাই-তো? এবার দেখাও তো তোমার সামনের ভেজা তলের মধ্যে দিয়ে -এর Flux (
) কত?
ভূপতি জানে এর দিশা বরাবর -এর উপাংশ হচ্ছে
। তাই এক ঝটকায় লিখে ফেললো
সুলতানা বললেন, দারুণ আয়ত্ত করেছো দেখছি। আর ভাবনা কী? দুটো Flux যোগ করে দাও। তাহলে পাওয়া যাবে। Flux তো স্কেলার রাশি। কোনো ঝামেলা নেই। ভূপতি লিখলো
সুলতানা বললেন, এটা বলে দেয় বৃষ্টি ক্ষেত্রের মধ্য দিয়ে যাওয়ার সময় প্রতি সেকেন্ডে তোমার শরীরে কত kg জলের ফোঁটা এসে পড়েছে। কেমন? এখন বার করতে হবে, গোটা রাস্তাটা পেরোলে মোট কত kg জল জমেছে। খুব সোজা। চারু তো জানে তুমি কী গতি নিয়ে যাচ্ছো। তাহলে বৃষ্টির মধ্যে একটা নির্দ্দিষ্ট পথ (ধরো ) যেতে তোমার কতটা সময় লাগবে (
) সে বার করতে পারবে না?
ভূপতি বললো, নিশ্চয় পারবে।
সুলতানা সঙ্গে সঙ্গে বলে উঠলেন, মানে ঠিক এই সময় ধরে তুমি ভিজেছো। তাহলে, তুমি যখন গন্তব্যে পৌঁছেছো, তখন তোমার শরীরে যতগুলো জলের ফোঁটা ধাক্কা মেরেছে তার মোট ভর হবে:
সমীকরণটাতে এক পলক তাকালেই পরিষ্কার বুঝতে পারবে -এর মান পুরোপুরি নির্ভর করে
-এর ওপর। আরও দেখো,
বাড়লে
-এর পরিমাণটা কমে। তাই তো? এবার মীমাংসা হলো তাহলে? আগের দিনের মতো বাড়ি ফেরার সময় দেখলে ঝেঁপে বৃষ্টি নেমেছে। ছাতা নেই কাছে। কী করবে?
ভূপতি প্রচণ্ড আবেগ নিয়ে বললো, রুদ্ধশ্বাসে ছুটবো। মনে আর কোনো দ্বিধা নেই।
সুলতানা বললেন, একদম। যত জোরে পারবে দৌড় লাগাবে। সাইকেল থাকলে ভালো। মোটরবাইক হলে কথাই নেই। খুব সামান্য ছাট গায়ে লাগবে।
ঠিক কত জোরে ছুটবো?
ভূপতি জিজ্ঞেস করলো, আচ্ছা দিদিমণি, u-টাকে যদি ক্রমশ বাড়াতেই থাকি, তাহলে নিশ্চয় এমন একটা পর্যায় আসবে, যখন আমি আর ভিজবোই না। শুকনো খটখটে অবস্থায় বাড়ি চলে আসবো। সেইরকম গতি কি আদৌ সম্ভব? সুলতানা খুব মন দিয়ে ভূপতির প্রশ্নটা শুনলেন। তারপর বললেন, গতি তুমি বাড়াতেই পারো। তবে, তোমার প্রশ্নটার উত্তর পেতে হলে আজ বাড়িতে গিয়ে ফের একটু খাটতে হবে। একটা অঙ্ক দিচ্ছি। করো। তুমি তো ভালই লম্বা। 6 ফুট হবে। আর তোমার ছাতি বিশ ইঞ্চি মনে হচ্ছে। এবার তোমার শরীরটাকে আমাদের কল্পনা করা Ellipsoid-টার সাথে তুলনা করো। তুমি বলতে পারো = 1.8 m আর
= 0.5 m। কোনো আপত্তি থাকা উচিত না। এই অবস্থায়, মনে করো
= 1 km।
-এর মান তো আগের দিন ক্লাসে বলে দিয়েছি। খুব আস্তে হাঁটলে
কত হয় তাও বলেছিলাম। এবার, কল্পনা করো
শুরুতে হচ্ছে ওরম। স্কুলে দৌড় প্রতিযোগিতায় যারা পদক জেতে, তাদের গতি মোটামুটি 5 m/s হয়। অলিম্পিকের অ্যাথলিট 10 m/s গতি নিয়ে দৌড়তে পারে। আর, জোরে মোটরবাইক চালালে গতি হয় 25 m/s। এবার প্রতিটা ক্ষেত্রে
বার করো তো। দিয়ে দেখো ভেজার পরিমাণ আগের থেকে কত শতাংশ করে কমছে। দেখবে তোমার প্রশ্নের উত্তর নিজেই পেয়ে যাবে।
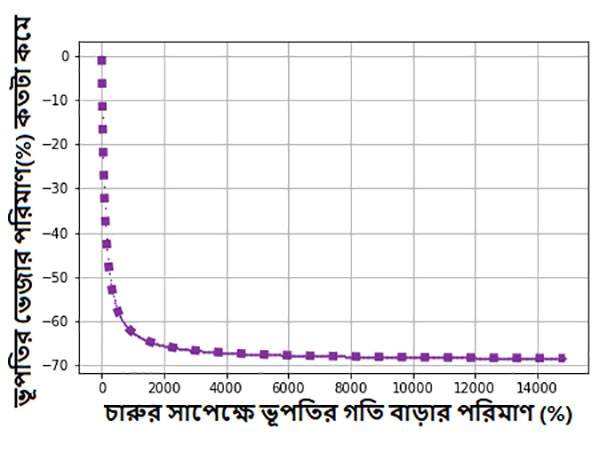
সন্ধে বেলাতেই ভূপতি আবার বাধ্য ছাত্রের মতো অঙ্কটা নিয়ে বসে গেলো। সূত্র তো জানা আছে। দেখা যাক উত্তর কী পাওয়া যায়। ভূপতি দেখলো প্রথম ক্ষেত্রে চারুর সাপেক্ষে ওর গতি আগের চেয়ে 400% বেড়েছে। ভেজার পরিমাণও অর্ধেকের বেশি (55.172 %) কমে গেছে। দ্বিতীয় ক্ষেত্রে এই গতি আরও 500% বেড়েছে। কিন্তু এবার ভেজার পরিমাণ আগের থেকে কমছে মাত্র 7% এর কাছাকাছি। তৃতীয় ক্ষেত্রে ওর গতি আগের চেয়ে 1500% বাড়লেও ভেজার পরিমাণ আগের চেয়ে কমেছে মাত্র 4%। সুতরাং, এককথায় সিদ্ধান্তে আসা যায় — বৃষ্টির মধ্যে হাঁটার চেয়ে ছুটলে ও কম ভেজে ঠিকই, কিন্তু এমন নয় পেল্লায় গতিতে গেলে এক্কেবারে না ভিজেই বাড়ি পৌঁছে যাবে। একটা সময় পর দেখা যাবে — গতি প্রচণ্ড পরিমাণে বাড়ছে। কিন্তু ভেজার পরিমাণ বড় একটা কমছে না।
একটি নির্দিষ্ট মানের পরে গতি যথেষ্ট পরিমাণ বাড়ালেও ভেজার পরিমাণ বড় একটা কমবে না। অর্থাৎ, বৃষ্টি তোমাকে কিছুটা তো ভেজাবেই।
পরদিন ভূপতির একগাল হাসি দেখে সুলতানা আন্দাজ করে নিলেন। তিনিও মুচকি হেসে বললেন, সব হেঁয়ালির জবাব পেলে তাহলে?
ভূপতি তার সব হিসেবনিকেশ আর উপরে লেখচিত্রটা দিদিমণিকে দেখালো। সব দেখে দিদিমণি খুব খুশি।
এরপর সুলতানা একটু মুচকি হেসে বললেন, একটা জিনিস কিন্তু ইচ্ছে করেই তোমাকে গতকাল বলিনি। আসলে এতো কাঠ-খড় না পুড়িয়েও কিন্তু তোমার সিদ্ধান্তে পৌঁছনো যায়। ভেবে দেখো, যত বাড়াবে,
অপেক্ষকের সমীকরণে
তত শূন্যের কাছাকাছি যাবে। কিন্তু সমীকরণের বাকি রাশিগুলো একই থাকবে। সুতরাং,
যা কিন্তু শূন্য নয়!

আবার এটাকে নিছক ছবি এঁকেও বোঝা যায়। চারুর দৃষ্টিভঙ্গি থেকে দেখলে তুমি -দিকে অতিক্রম করছো
পরিমাণ দূরত্ব। তোমার সামনের লম্বচ্ছেদের ক্ষেত্রফল
। অর্থাৎ তুমি
আয়তনের একটা অঞ্চল অতিক্রম করে যাচ্ছো। যেহেতু বৃষ্টি কেবল উল্লম্ব ভাবে পড়ছে তাই তোমার সামনেটা কতটা ভিজবে সেই গণনা করতে গেলে বৃষ্টির জলকে স্থিতিশীল ধরে নেওয়া যায়। অর্থাৎ এই অঞ্চলে যতটা জল রয়েছে তার পুরোটাই তোমার সামনেটাকে ভেজাবে। সে যত আস্তেই বা জোরেই তুমি যাও না কেন। যেহেতু আমরা
ধরে নিয়েছি আগে, তাই —
আরও আরও প্রশ্ন
দিদিমণির প্রশ্নের শেষ নেই। তিনি এরপর বললেন, আরেকটা জিনিস করে দেখতে পারো। -টা শুধু
নয়, তোমার
ও
-এর অনুপাতের ওপরও নির্ভর করে। কিন্তু ঠিক কীভাবে?
একজন রোগা, লম্বা লোক আর একজন মোটা খাটো লোক বৃষ্টিতে পাশাপাশি হাঁটলে বা ছুটলে কে বেশি ভিজবে?
শেষে দিদিমণি বললেন, আমরা কিন্তু সহজ একটা সমস্যা দিয়ে শুরু করেছিলাম। এবার আসল সমস্যাটার দিকে এগোতে পারো। যদি হাওয়া চলে, তাহলে নির্ভর করবে জলের ফোঁটা হাওয়ার দিক অনুযায়ী কোনদিকে বাঁক নিয়েছে তার ওপর। ফলে, -এর উপাংশগুলো আর আগের মতো থাকবে না। তবে,
ও
গণনা করার নিয়ম একই থাকবে। জটিলতা এড়াতে আমরা ধরে নিয়েছিলাম,
আর
একই সমতলে
আছে। চারুর সাপেক্ষে ভূপতি যেদিকে যাচ্ছে, হাওয়া তার আড়ে চললে সেই শর্তও মানা হয় না। তখন
। আগের Flux গুলোর সাথে
-ও বার করতে হয়। এরপর তিনটে Flux যোগ করে আগের মতো
হিসাব করতে হবে। যাকগে, আজ আর কোনো কাজ নয়। বাড়ি গিয়ে মনটাকে আরাম দাও। অনেক অঙ্ক হয়েছে। ভূপতি দিদিমণির কাছে বিদায় নিলো। কিন্তু ওর বেশ চাঙ্গা লাগছে। খিদে এখনও মেটেনি। ওর এক বন্ধু আছে অমল। অঙ্কে চোস্ত। ও ঠিক করলো দিদিমণির পরের প্রশ্নটা নিয়ে অমলের সাথে বসতে হবে।
টীকা:
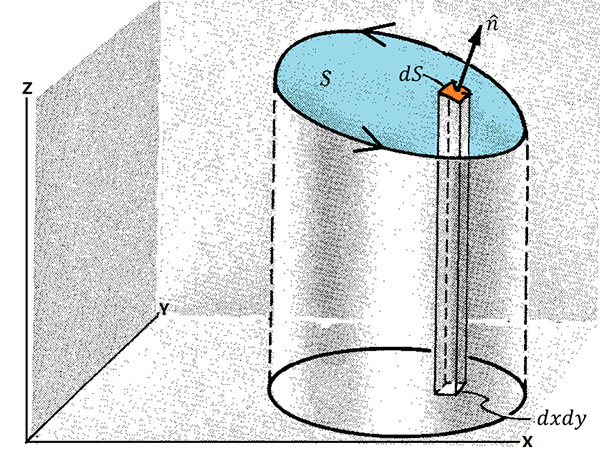
ধরা যাক, ক্ষেত্রের মধ্যে একটা মুক্ত তল(
) আছে। প্রথমে, ঐ তলের একটা খুব ছোট্ট অংশ নেওয়া হয়েছে। এত ছোট যে এটা পুরো সমতল।
এর ক্ষেত্রফল [
হলো
-এর দিকে একক ভেক্টর]
তবে, -এর মধ্য দিয়ে
-এর Flux
[যেখানে, বরাবর
-এর উপাংশ
]
মনে করি, ,
ও
অক্ষের +ve দিশা বরাবর একক ভেক্টর যথা:
,
এবং
। তবে,
ফলে, গোটা -এর মধ্য দিয়ে
ক্ষেত্রের Flux:
প্রচ্ছদের ছবি: অনিন্দ্য চট্টোপাধ্যায় (BCCL)
কৃতজ্ঞতা স্বীকার:
১। Franco Bocci 2012 Eur. J. Phys. 33 1321
২। SCHAUM’S OUTlines VECTOR ANALYSIS, M.R.SPIEGEL
লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।
Scan the above code to read the post online.
Link: https://bigyan.org.in/should-we-run-in-rain
