21-11-2024 09:48:50 am

print

 

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

 

সঙ্গীত স্বরগ্রামের বিজ্ঞান: পাশ্চাত্য সঙ্গীত

%e0%a6%b6%e0%a7%81%e0%a6%ad%e0%a6%be-%e0%a6%b8%e0%a6%be%e0%a6%ae%e0%a6%a8%e0%a7%8d%e0%a6%a4
শুভা সামন্ত

(স্কটিশ চার্চ কলেজ)

 
09 Sep 2022
 

Link: https://bigyan.org.in/science-of-music-western-01

%e0%a6%b8%e0%a6%99%e0%a7%8d%e0%a6%97%e0%a7%80%e0%a6%a4-%e0%a6%b8%e0%a7%8d%e0%a6%ac%e0%a6%b0%e0%a6%97%e0%a7%8d%e0%a6%b0%e0%a6%be%e0%a6%ae%e0%a7%87%e0%a6%b0-%e0%a6%ac%e0%a6%bf%e0%a6%9c%e0%a7%8d%e0%a6%9e

যেকোনো একটি সাঙ্গীতিক স্বর (যেমন হারমোনিয়ামের “সা” অথবা “রে” অথবা “গা”) আসলে অনেকগুলো সুরের সমন্বয়ে তৈরী যাদের কম্পাঙ্ক f, 2f, 3f,⋯ এই শ্রেণীতে বাড়তে থাকে। এই একেকটি সুর হলো শব্দের একেকটি সাইন-তরঙ্গ (sine wave)। কোনো একটি স্বরে সর্বনিম্ন কম্পাঙ্কের (f) সুরটি সবথেকে জোরালো হয় এবং পরবর্তী কম্পাঙ্কের সুরগুলো উত্তরোত্তর কম জোরালো হতে থাকে। এই f কে বলা হয় স্বরটির মূলকম্পাঙ্ক (fundamental frequency) এবং পরবর্তী সুরগুলোকে বলা হয় সমমেল (harmonic)। এখন দুটি স্বরের মূলকম্পাঙ্কের অনুপাত যদি 2/1, 3/2, 4/3, 5/4,⋯ এইরকম দুটো ছোট ছোট পূর্ণসংখ্যার অনুপাত হিসেবে লেখা যায়, তাহলে তাদের কিছু অপেক্ষাকৃত জোরালো সমমেলের কম্পাঙ্ক মিলে যাবে। এইরকম দুটি স্বর একসাথে বা একটির পর আর একটি খুব তাড়াতাড়ি বাজালে আমাদের কানে তাদের সঙ্গতি মধুর শোনায়। আশ্চর্যের বিষয় হলো এই সুন্দর গাণিতিক-নিয়ম-মানা স্বর-সঙ্গতিই সঙ্গীতসৃষ্টির মূল উপাদান, তা পাশ্চাত্য সঙ্গীত হোক বা ভারতীয় সঙ্গীত। এই গাণিতিক নিয়মটি থেকেই স্বরগুলির অবস্থান (অর্থাৎ মূলকম্পাঙ্ক) নির্ণয়ের তত্ত্ব থেকে শুরু করে আরও নানা সাঙ্গীতিক ধারণার উৎপত্তি হয়েছে। আজকের পর্বে লেখিকা পাশ্চাত্য সঙ্গীতের পটভূমিতে গণিত ও পদার্থবিজ্ঞানের এই আশ্চর্য প্রয়োগ নিয়ে আলোচনা করেছেন। আগামী পর্বে থাকবে ভারতীয় সঙ্গীত নিয়ে আলোচনা।

‘আমি শুনব ধ্বনি কানে,
আমি ভরব ধ্বনি প্রাণে,
সেই ধ্বনিতে চিত্তবীণায় তার বাঁধিব বারে বারে।।’

সুর ও স্বর

আমরা সকলেই জানি সঙ্গীত হলো স্বরসমূহের এমন এক বৈশিষ্ট্যপূর্ণ রচনা যা মানুষের চিত্তকে প্রসন্ন করতে সক্ষম। কিন্তু প্রতিদিনের কথাবার্তায় “স্বর” শব্দটা আমরা নানাভাবে ব্যবহার করলেও সঙ্গীত ও শব্দবিজ্ঞানের (acoustics) চর্চায় এর একটা বিশেষ অর্থ আছে। সেই অর্থটা শুরুতে ছোট্ট করে জেনে নেওয়া যাক।

একটিমাত্র কম্পাঙ্কবিশিষ্ট শব্দকে বলে সুর আর বিভিন্ন কম্পাঙ্কের কয়েকটি সুর একসাথে ধ্বনিত হলে যে শব্দের সৃষ্টি হয়, তাকে বলা হয় স্বর। উদাহরণ হিসাবে বলা যায়, সুরশলাকার কম্পনে সৃষ্ট শব্দ হলো সুর আর বিভিন্ন সাঙ্গীতিক যন্ত্র থেকে উদ্ভূত শব্দ হলো স্বর। তাহলে, যেকোনো স্বর অনেকগুলি পৃথক পৃথক কম্পাঙ্কের সুরের সমন্বয়ে গঠিত। সর্বনিম্ন মানের কম্পাঙ্কটিকে, যার মান ধরা যাক f_1, মূলকম্পাঙ্ক বলা হয়। মূলকম্পাঙ্ক ব্যতীত অন্যান্য কম্পাঙ্কের সুরগুলিকে বলা হয় উপসুর বা overtone। আবার যেসমস্ত সুরগুলির কম্পাঙ্ক মূলকম্পাঙ্কের পূর্ণ গুণিতক (অর্থাৎ 2f_1, 3f_1, \cdots) তাদের সমমেল বা harmonic বলে। তাহলে বলা যায়, মূলকম্পনই হলো প্রথম সমমেল। স্পষ্টত সব সমমেলই উপসুর, কিন্তু সব উপসুর সমমেল নয়। যেমন কোনো ধ্বনিতে উপস্থিত একটি সুরের কম্পাঙ্ক যদি মূলকম্পাঙ্কের দেড় (1.5f_1) বা আড়াই গুণ (2.5f_1) হয়, তাহলে তাদের সমমেল বলা যাবে না, বলতে হবে উপসুর।

সব সমমেলই (harmonic) উপসুর (overtone), কিন্তু সব উপসুর সমমেল নয়। কিন্তু একটি সাঙ্গীতিক স্বরের ক্ষেত্রে সবকটি উপসসুরই সমমেল হয়। সমমেলগুলির উপস্থিতিই সাঙ্গীতিক ধ্বনির শ্রুতিমধুরতার কারণ।

কিন্তু একটি সাঙ্গীতিক স্বরের ক্ষেত্রে সবকটি উপসসুরই সমমেল হয়। অর্থাৎ যেকোনো একটি সাঙ্গীতিক স্বরে উপস্থিত সুরগুলির কম্পাঙ্ক মূলকম্পাঙ্কের পূর্ণ গুণিতক। সমমেলগুলির উপস্থিতিই সাঙ্গীতিক ধ্বনির শ্রুতিমধুরতার কারণ। তবে স্বরের কম্পাঙ্ক বলতে মূলসুরটির কম্পাঙ্ককেই বোঝানো হয়। স্বরের একাধিক কম্পনের মধ্যে মূলকম্পাঙ্কের কম্পনটি সবচেয়ে জোরালো এবং অন্যান্য কম্পনগুলির জোর ক্রমশ কমতে থাকে । প্রসঙ্গত, এই (f_1, 2f_1, 3f_1, \cdots) শ্রেণিটিকে স্বরটির সমমেল-শ্রেণী বলা হয়।

অঙ্কের ভাষায় দেখলে, একটি সাঙ্গীতিক স্বরের তরঙ্গরূপটি সময়ের সাথে পর্যায়বৃত্ত হয় (periodic in time)। সুতরাং Fourier শ্রেণীর তত্ত্ব অনুযায়ী তরঙ্গরূপটিকে অনেকগুলি sine এবং cosine তরঙ্গে ভেঙে ফেলা যায়, যাদের সবার কম্পাঙ্ক একটা মূলকম্পাঙ্কের পূর্ণ গুণিতক। এই sine ও cosine তরঙ্গগুলোই এক-একটা সুর। দেখা যাচ্ছে এক্ষেত্রে মূলকম্পন ব্যতীত অন্য সবকটি উপসুরই সমমেল। 

পাশ্চাত্য সঙ্গীতের পরিভাষা

পাশ্চাত্য সঙ্গীতের ভিত্তি গঠন করেছে সাতটি “শুদ্ধ” স্বর যেগুলি চিহ্নিত করার জন্য ইংরাজী বর্ণমালার A থেকে G পর্যন্ত অক্ষর এবং ক্ষেত্রবিশেষে সংখ্যার রোমক চিহ্ন ব্যবহৃত হয়। সাতটি স্বরের সাধারণ নাম হলো Do, Re, Mi, Fa, Sol, La, Ti। স্বরগুলির সাধারণ ক্রম নিম্নরূপ:

CDEFGAB
IIIIIIIVVVIVII

এর মানে অবশ্য এই নয় যে, সবসময়ই Do মানে C, Re মানে D ইত্যাদি।  Do, Re, Mi, Fa ইত্যাদি যথাক্রমে B, C, D, E এই ক্রমেও হতে পারে। স্বরকে ইংরাজীতে বলা হয় নোট (note) । রোমক চিহ্ন I দ্বারা সূচিত প্রথম নোট (এখানে C) কে বলা হয় টোনিক (tonic)। উপরের সারিতে টোনিক থেকে শুরু করে স্বরগুলোর কম্পাঙ্ক ক্রমশ বাড়তে থাকে। B-এর পরবর্তী স্বরটিকে আবার C দিয়ে চিহ্নিত করা হয় এবং এই C এর কম্পাঙ্ক আগের C এর কম্পাঙ্কের ঠিক দ্বিগুণ হয়। C থেকে পরের C পর্যন্ত আটটি স্বরের সমষ্টি নিয়ে তৈরী হয় অক্টেভ (octave)। তাছাড়া, যেকোনো স্বরের দ্বিগুণ কম্পাঙ্কের স্বরটিকেও প্রথমোক্ত স্বরের অক্টেভ বলা হয়। 

শুদ্ধ স্বরের পাশাপাশি আছে কড়ি বা তীব্র স্বর এবং কোমল স্বর। ইংরাজীতে কড়িকে বলা হয় শার্প (sharp) এবং কোমলকে বলা হয় ফ্ল্যাট (flat)। কোনো একটি শুদ্ধ স্বরের সাপেক্ষে উচ্চতর কম্পাঙ্কের স্বর বোঝাতে ব্যবহৃত শার্প শব্দটির প্রতীক ♯ এবং নিম্নতর কম্পাঙ্কের স্বর বোঝাতে ব্যবহৃত ফ্ল্যাট শব্দটির প্রতীক ♭। প্রত্যেকটি স্বরকেই কড়ি বা কোমল করা যেতে পারে। শুদ্ধ স্বরগুলিকে বলা হয় ন্যাচারাল (natural)।

স্কেল বা স্বরগ্রাম

সঙ্গীত রচনা বা পরিবেশন করার সময় কয়েকটি বিশেষ স্বরকে বেছে নিয়ে কেবল সেইগুলি রচনাটিতে ব্যবহার করা হয়। ভাষার যেমন বর্ণমালা থাকে এও ঠিক সেরকম একধরনের সাঙ্গীতিক বর্ণমালা। সঙ্গীতে ব্যবহৃত স্বরসমূহের একটি সুবিন্যস্ত ক্রমকে স্কেল বা স্বরগ্রাম বলা হয়। সঙ্গীত স্বরগ্রামের উৎপত্তির ইতিহাস পদার্থবিদ্যার সঙ্গে অঙ্গাঙ্গীভাবে জড়িত এবং এটি তরঙ্গগতিবিদ্যার একটি আকর্ষণীয় প্রয়োগ। এই বিষয়টা নিয়েই আমরা আজ আলোচনা করবো।

আমাদের শ্রবণযন্ত্রে শব্দ লগারিদমিক স্কেলে অনুভূত হয় অর্থাৎ বিভিন্ন স্বর তাদের কম্পাঙ্কের পার্থক্যের বদলে কম্পাঙ্কের অনুপাত দ্বারা আমাদের মস্তিষ্কে সম্বন্ধযুক্ত থাকে। তাই, সঙ্গীতের সমস্ত স্কেলকেই একটি প্রাথমিক স্বরের সাপেক্ষে অন্যান্য স্বরের কম্পাঙ্কের অনুপাত দ্বারা সংজ্ঞায়িত করা হয়।

আমাদের শ্রবণযন্ত্রে শব্দ লগারিদমিক স্কেলে অনুভূত হয় অর্থাৎ বিভিন্ন স্বর তাদের কম্পাঙ্কের পার্থক্যের বদলে কম্পাঙ্কের অনুপাত দ্বারা আমাদের মস্তিষ্কে সম্বন্ধযুক্ত থাকে।

স্বরের কম্পাঙ্ক সম্পর্কিত আলোচনায় আমরা মূলকম্পাঙ্কটিরই উল্লেখ করবো। তাহলে বলা যায় যে প্রতিটি স্বরের একটি নির্দিষ্ট কম্পাঙ্ক আছে। একই কম্পাঙ্কের দুটি স্বর যুগপৎ অনুরণিত হলে তাদের বলা হয় ঐক্যবদ্ধ স্বর (notes in unison)। আবার দ্বিতীয় স্বরের কম্পাঙ্ক প্রথম স্বরের কম্পাঙ্কের দ্বিগুণের কাছাকাছি হলে আমাদের মস্তিষ্কের অনুভূতিতে সেইদুটি স্বরের স্বাতন্ত্র্য লুপ্ত হয়। সঙ্গীতে এই স্বরদুটিকে একই স্বর হিসাবে ধরা হয়, যদিও তাদের কম্পাঙ্ক আলাদা। পাশ্চাত্য সঙ্গীতে এই স্বরদুটিকে বলা হয় এক অক্টেভ দূরবর্তী দুটি স্বর। দুটি স্বরের কম্পাঙ্কের ব্যবধান যদি অক্টেভ বা অষ্টকের পূর্ণ গুণিতক হয়, তাহলে সঙ্গীতের ভাষায় তারা সমতুল্য এবং সঙ্গীতের স্বরলিপিতে তাদের একই নাম দ্বারা চিহ্নিত করা হয়।  

সঙ্গীতের একটি গুরুত্বপূর্ণ বিষয় হলো স্বরসঙ্গতি। যদি দুটি স্বরের যুগপৎ ধ্বনি আমাদের কানে মধুর শোনায়, তাহলে তাদের বলা হয় সঙ্গতিপূর্ণ স্বর। একটি স্বরের সঙ্গে অপর একটি স্বরের সামঞ্জস্যপূর্ণ মধুর সঙ্গতিকে বলা হয় শুভ স্বর-সম্বাদ। ইংরাজী ভাষায় একে বলা হয় consonance। এই স্বর-সম্মেলন আমাদের কাছে মনোরঞ্জক। যদি দুটি স্বরের সঙ্গতির মধ্যে মাধুর্য না থাকে, তবে সেই ঘটনাকে বলা হয় বিসম্বাদ বা dissonance। স্কেল গঠনকারী স্বরগুলি এমনভাবে বিন্যস্ত থাকে যাতে দুটি বা তার বেশি স্বরকে একসাথে বা একটি স্বরের পর আর একটি স্বর অতিশীঘ্র ধ্বনিত করলে সম্ভাব্য সঙ্গতিপূর্ণ সমবায় সর্বোচ্চ সংখ্যায় উপস্থিত থাকে বা বিসম্বাদের নজির ন্যূনতম হয়। তবে বিসম্বাদ বা dissonance খানিক অস্বস্তি তৈরী করলেও ক্ষেত্রবিশেষে সঙ্গীতের মেজাজ সৃষ্টি করতে এরও প্রয়োগ করা হয়।  Consonant এবং dissonant স্বর উভয়েই সঙ্গীতে গুরুত্বপূর্ণ ভূমিকা পালন করে। Consonance এবং dissonance এর উদাহরণ কানে শুনতে এই ভিডিওটি দেখুন।

স্কেলের ধারণা তৈরী হয়েছে স্বরসঙ্গতির ওপর ভিত্তি করে। সঙ্গতির বিষয়টি beats বা স্বরকম্পের ঘটনা দ্বারা ব্যাখ্যা করা যায়। এখন তাহলে এই স্বরকম্প ব্যাপারটা কী, তা একটু জেনে নেওয়া যাক। 

শব্দের একটি বৈশিষ্ট্য হলো তার প্রাবল্য। প্রাবল্য বলতে বোঝায় শব্দ কতটা জোরালোভাবে আমাদের কানে এসে পৌঁছাচ্ছে। প্রাবল্য নির্ভর করে শব্দতরঙ্গের বিস্তারের (amplitude) ওপর। আবার সুরযুক্ত শব্দের যে বৈশিষ্ট্যের জন্য একই প্রাবল্যের চড়া (সরু) এবং খাদের (মোটা) সুরের মধ্যে পার্থক্য বোঝা যায়, তাকে শব্দের তীক্ষ্ণতা বলে। এটি শব্দতরঙ্গের কম্পাঙ্কের সঙ্গে সম্বন্ধযুক্ত একটি ধারণা। কম্পাঙ্ক বাড়লে তীক্ষ্ণতা বাড়ে, ফলে সুর চড়া শোনায়। অন্যদিকে কম্পাঙ্ক কমলে তীক্ষ্ণতা কমে, ফলে সুর মোটা হয়।

খাদের স্বর
চড়ার স্বর

প্রায় সমান তীক্ষ্ণতা এবং সমান বা প্রায় সমান প্রাবল্যের দুটি সুর যদি একসঙ্গে উৎপন্ন করা যায়, তবে শ্রুত শব্দের প্রাবল্য পর্যায়ক্রমে বাড়তে ও কমতে থাকে। শব্দের প্রাবল্যের এই বাড়া-কমাকে স্বরকম্প বলা হয়।

স্বরকম্প

লব্ধি তরঙ্গের বিস্তারের একবার বাড়া ও একবার কমা নিয়ে একটি স্বরকম্প গঠিত হয়। প্রমাণ করা যায় যে, প্রতি সেকেণ্ডে স্বরকম্পের সংখ্যা বা স্বরকম্পাঙ্ক, উপরিপাতিত তরঙ্গদুটির কম্পাঙ্কের পার্থক্যের সমান হয়। শব্দতরঙ্গের ক্ষেত্রে তরঙ্গদুটির কম্পাঙ্কের পার্থক্য 10 হার্ৎসের বেশি না হলে তবেই স্বরকম্প স্পষ্ট শোনা যায়। কারণ স্বরকম্পাঙ্ক খুব বেশি হলে আমাদের কান প্রাবল্যের বাড়া-কমা আলাদাভাবে বুঝতে পারে না। তখন এই শব্দ একটি একটানা স্বর হিসাবে শ্রুত হয়।  আবার দুটি শব্দতরঙ্গের বিস্তারের পার্থক্য যত বেশি হয় অর্থাৎ একটি শব্দ অপরটির তুলনায় যত ক্ষীণ হয়, তাদের যুগপৎ ধ্বনির বিস্তারের বাড়া-কমা তত কম হয়। প্রাবল্যের হেরফের খুব কম হওয়ার দরুন স্বরকম্পগুলি সাধারণত শ্রুতিবোধ্য হয় না। 

স্বরদ্বয়ের কম্পাঙ্ককে যদি দুটি ক্ষুদ্র পূর্ণসংখ্যার অনুপাত দ্বারা প্রকাশ করা যায়, তাহলে তাদের যুগপৎ ধ্বনি শুভ স্বর-সম্বাদ সৃষ্টি করে। এইরকম তিনটি সর্বাধিক গুরুত্বপূর্ণ অনুপাত হলো 2/1, 3/2 এবং 4/3। তবে অনুপাতগুলো কিন্তু কাঁটায় কাঁটায় হওয়া চাই। সেক্ষেত্রে দুটি স্বরের একাধিক সমমেল সমাপতিত হয়। এই অনুপাতের সামান্য অসঙ্গতি হলেই দুটি স্বরের অনুরূপ সমমেলগুলির মধ্যে কম্পাঙ্কের নিরিখে স্বল্প দূরত্ব সৃষ্টি হয় এবং স্বরকম্পের দরুন বিসম্বাদ ঘটতে পারে।

শুভ স্বর-সম্বাদ এবং বিসম্বাদের ঘটনাটি সংশ্লিষ্ট স্বরগুলির সমমেলের বিন্যাসের ওপর নির্ভর করে। আগের অনুচ্ছেদে উল্লিখিত সমমেল সমাপতনের বিষয়টি বোঝার জন্য f_1 এবং f_2 = \frac{3}{2}f_1 কম্পাঙ্ক-বিশিষ্ট দুটি স্বর বিবেচনা করা যাক। সঙ্গীতের পরিভাষায় প্রথম স্বরের সাপেক্ষে দ্বিতীয় স্বরটিকে বলা হয় সাঙ্গীতিক পঞ্চম বা musical fifth। f_1 মূলকম্পাঙ্ক-বিশিষ্ট স্বরের সমমেল গুলির কম্পাঙ্ক f_1, 2f_1, 3f_1, \cdots। অনুরূপভাবে f_2 মূলকম্পাঙ্ক-বিশিষ্ট স্বরের সমমেল গুলির কম্পাঙ্ক f_2, 2f_2, 3f_2, \cdots।  ১ নং ছবিতে দুটি স্বরের সমমেলগুলির বিন্যাস ও তাদের উপরিপাতের দরুন সৃষ্ট ধ্বনিতে উপস্থিত উপসুরগুলির বিন্যাস দেখানো হয়েছে। যথাযথ পঞ্চমভাবযুক্ত দুটি  স্বরের  কতিপয়  সমাপতিত

১ নং ছবি: f_1 ও f_2 = (\frac{3}{2}f_1) মূলকম্পাঙ্ক-বিশিষ্ট স্বরে উপস্থিত সমমেল এবং তাদের উপরিপাতিত স্বরে বিদ্যমান উপসুরগুলির বিন্যাস।

সমমেল ছবি থেকে দেখা যাচ্ছে। যেমন f_1 কম্পাঙ্কের স্বরের তৃতীয় সমমেলের এবং f_2 কম্পাঙ্কের স্বরের দ্বিতীয় সমমেলের কম্পাঙ্ক সমান। এরপর, f_1 কম্পাঙ্কের স্বরের ষষ্ঠ সমমেলের কম্পাঙ্ক f_2 কম্পাঙ্কের স্বরের চতুর্থ সমমেলের কম্পাঙ্কের সমান। এইভাবে আরও সমাপতিত সমমেল গণনা করা যেতে পারে। তবে আগেই বলা হয়েছে, যেকোনো স্বরেরই উচ্চতর সমমেলগুলির জোর ক্রমশ কমতে থাকে। তাই, প্রথম কয়েকটির পর বাকি সমমেলগুলির অস্তিত্ব প্রায় থাকে না বললেই চলে।

এখন, f_1 এবং  f_2 কম্পাঙ্কের যেকোনো দুটি স্বরের যুগপৎ উপস্থিতিতে আর একটা অদ্ভুত ঘটনা ঘটে। সেক্ষেত্রে এই দুটি স্বরের কম্পাঙ্কের অন্তরফল \Delta f = f_2 - f_1 বিশিষ্ট কম্পাঙ্কের একটা আরও একটা শব্দ শুনতে পাওয়া যায়। এটা যে ঠিক কেন হয় তা আজও বিজ্ঞানীদের গবেষণার বিষয়, তবে মনে করা হয় আমাদের শ্রবণযন্ত্রের অরৈখিক প্রতিক্রিয়ার (nonlinear response) ফলেই এমনটা হয়ে থাকে। ইতালীয় বেহালাবাদক তারতিনির (Giuseppe Tartini) নামে এই সুরের নাম দেওয়া হয়েছে তারতিনির সুর (Tartini’s tone)।

আমাদের বর্তমান আলোচনায় f_1 এবং f_2 = \frac{3}{2}f_1 এই দুটি স্বরের কম্পাঙ্কের অন্তরফল f_2 - f_1 = \frac{3}{2}f_1 - f_1 = \frac{1}{2}f_1 যা f_1 কম্পাঙ্কের স্বরের অক্টেভ সমতুল স্বরের কম্পাঙ্ক। সুতরাং, যথাযথ পঞ্চম-ভাব যুক্ত দুটি স্বরের যুগপৎ ধ্বনিতে উপস্থিত কম্পাঙ্ক সমূহের মধ্যে প্রথম তিনটি হলো (\frac{1}{2}f_1, f_1, \frac{3}{2}f_1), যা একটি সমমেল-শ্রেণী গঠন করে। তাই এই ধ্বনি মানুষের শ্রবণ-স্নায়ুতন্ত্রে শ্রুতিমধুর আওয়াজ রূপে অনুভূত হয়।  সাঙ্গীতিক স্কেলের অন্যান্য ব্যবধানযুক্ত স্বরের জন্যও অনুরূপ বিশ্লেষণ করে বলা যায় যে, সঙ্গতির ক্রমহ্রাসমান ব্যবধান বিন্যাস হলো 2/1 > 3/2 > 4/3 > 5/4 > 5/3। স্পষ্টতই এই বিন্যাসটি লেখা হয়েছে একটি স্বরের সঙ্গে অন্য স্বরের কতগুলো সমমেল সমাপতিত হয় (কম্পাঙ্কের একটি নির্দিষ্ট পরিসরে) তার নিরিখে। সর্বোপরি, দুটি স্বরের যুগপৎ ধ্বনিতে উপস্থিত উপসুরগুলির কম্পাঙ্কের ব্যবধান যত বেশি হয়, স্বরকম্পজনিত সমস্যা তত কম ঘটে। কারণ, দুটি সুরের কম্পাঙ্কের ব্যবধান বাড়লে, স্বরকম্পাঙ্ক বাড়ে, সেক্ষেত্রে মানুষের কান প্রাবল্যের বাড়া-কমা আলাদাভাবে বুঝতে পারে না।

3:2 আনুপাতিক কম্পাঙ্কের দুটি স্বরের যুগপৎ ধ্বনি
16:15 আনুপাতিক কম্পাঙ্কের দুটি স্বরের যুগপৎ ধ্বনি

সুতরাং, মানুষের শ্রবণযন্ত্রের শব্দ অনুভবের বিষয়টি সঙ্গীতের স্কেল বা স্বরগ্রাম গঠনের মূল। আগেই বলা হয়েছে সাঙ্গীতিক স্কেল হলো কয়েকটি স্বরের সমাহার যা সঙ্গীতের ভিত্তি হিসাবে কাজ করে। বিভিন্ন বর্ণ যেমন ভাষার ভিত গঠন করে, স্বরগুলি তেমনি সঙ্গীতের ভিত তৈরি করে। এক্ষেত্রে দুটি স্বরের উপরিপাতের ফলে সৃষ্ট স্বরকম্পের ধারণা সর্বাধিক গুরুত্বপূর্ণ। স্বরকম্পের ঘটনাটি যাতে সঙ্গীতের মাধুর্য নষ্ট না করে, তা নিশ্চিত করতেই বিভিন্ন স্কেলের সৃষ্টি হয়েছে।

মানুষের শ্রবণযন্ত্রের শব্দ অনুভবের বিষয়টি সঙ্গীতের স্কেল বা স্বরগ্রাম গঠনের মূল। স্বরকম্পের ঘটনাটি যাতে সঙ্গীতের মাধুর্য নষ্ট না করে, তা নিশ্চিত করতেই বিভিন্ন স্কেলের সৃষ্টি হয়েছে।

সাঙ্গীতিক স্কেলের বিভিন্ন স্বরগুলি তাদের কম্পাঙ্কের ভিত্তিতে ক্রমানুসারে সাজানো থাকে। যে স্কেলে স্বরগুলি ক্রমবর্ধমান কম্পাঙ্ক অনুযায়ী সাজানো থাকে, তাকে আরোহ এবং ক্রমহ্রাসমান কম্পাঙ্ক অনুযায়ী সাজানো স্বরগুলি দিয়ে গঠিত স্কেলকে অবরোহ বলা হয়। একটি স্কেলের বিস্তার হয় এক অষ্টক। অর্থাৎ সাঙ্গীতিক স্কেল একটি অষ্টকের ব্যবধানকে নির্দিষ্ট সংখ্যক ভাগে ভাগ করে।  এই ভাগগুলি অর্থাৎ পরপর দুটি স্বরের মধ্যবর্তী ব্যবধান সমান বা অসমান দুইই হতে পারে। এখানে বিশেষভাবে উল্লেখ করা প্রয়োজন যে, দুটি স্বরের মধ্যবর্তী ব্যবধান বা স্বরান্তর মাপা হয় স্বরদুটির কম্পাঙ্কের অনুপাত দিয়ে। অষ্টকের অন্তর্গত স্বরের সংখ্যা ও তাদের ব্যবধানের ভিত্তিতে গঠিত একাধিক স্কেলের অস্তিত্ব আছে যেগুলি আমরা একে একে আলোচনা করবো।

পিথাগোরীয় স্কেল  

বাদ্যযন্ত্রকে বাঞ্ছিত সুরে বাঁধার জন্য উদ্ভূত প্রাচীন স্কেলগুলির মধ্যে অন্যতম হলো পিথাগোরীয় স্কেল। বিখ্যাত গণিতবিদ ও দার্শনিক পিথাগোরাস দুটি মূলনীতির ওপর ভিত্তি করে অষ্টকের অন্তর্গত সঙ্গতিপূর্ণ স্বরসমূহের অবস্থান স্থির করেন—নীতিদুটি হলো অক্টেভ সমতুল্যতা এবং পঞ্চম সঙ্গতি। অর্থাৎ পিথাগোরীয় স্কেল যে দুটি অনুপাতের ভিত্তিতে গড়ে উঠেছে তা হলো 2/1 এবং 3/2। এবার এই স্কেলের স্বরগুলি কিভাবে পাওয়া যায় দেখা যাক।  ধরা যাক, প্রাথমিক স্বরের মূলকম্পাঙ্ক f। পঞ্চম ভাবযুক্ত স্বরগুলির ব্যবধান যথাযথ রাখার জন্য প্রাথমিক স্বর থেকে শুরু করে পুনঃপুনঃ 3/2 গুণ বা ভাগ করা এই স্কেল গঠনের মূলনীতি। সেক্ষেত্রে কোনো কোনো ধাপে প্রাপ্ত কম্পাঙ্ক, প্রাথমিক স্বরের সাথে সংশ্লিষ্ট অষ্টকের উচ্চে বা নিম্নে অবস্থিত হবে। এই জায়গায় অষ্টক সমতুল্যতার নীতি কাজে লাগানো হয়। এই নীতি অনুযায়ী, 2-এর প্রয়োজনীয় ঘাত ভাগ বা গুণ করে প্রাথমিক স্বরের সাথে সংশ্লিষ্ট অষ্টকের মধ্যে কম্পাঙ্কগুলিকে ফিরিয়ে আনা হয়।

বিখ্যাত গণিতবিদ ও দার্শনিক পিথাগোরাস দুটি মূলনীতির ওপর ভিত্তি করে অষ্টকের অন্তর্গত সঙ্গতিপূর্ণ স্বরসমূহের অবস্থান স্থির করেন—নীতিদুটি হলো অক্টেভ সমতুল্যতা এবং পঞ্চম সঙ্গতি।

প্রথম ধাপ:

f মূলকম্পাঙ্ক-বিশিষ্ট প্রাথমিক স্বর থেকে শুরু করে সাঙ্গীতিক পঞ্চমের যে ক্রমোচ্চ বিন্যাস পাওয়া যায়, তা নিচে দেখানো হয়েছে।

f(3/2)f(3/2)^2f(3/2)^3f(3/2)^4f(3/2)^5f
f(3/2)f(9/4)f(27/8)f(81/16)f(243/32)f
(১)

দ্বিতীয় ধাপ:

উপরের সারি থেকে দেখা যাচ্ছে, সব স্বরগুলি আমাদের আলোচ্য অষ্টকের মধ্যে নেই। ১ নং বিন্যাস ক্রমের মধ্যে \frac{9}{4}f এবং তার পরবর্তী কম্পাঙ্কগুলি আলোচ্য অষ্টকের ঊর্ধ্বে অবস্থিত। সংশ্লিষ্ট অষ্টকের মধ্যে \frac{9}{4}f এবং \frac{27}{8}f কম্পাঙ্কের স্বরদুটির সমতুল স্বরের কম্পাঙ্ক যথাক্রমে \frac{9}{8}f ও \frac{27}{16}f। আবার \frac{81}{16}f ও \frac{243}{32}f কম্পাঙ্কের স্বর দুটির অবস্থান বিবেচ্য ব্যবধানের দুই অষ্টক ঊর্ধ্বে। সুতরাং, নির্ধারিত অষ্টকের মধ্যে এই দুই স্বরের সমতুল্য স্বর দুটি পেতে উক্ত কম্পাঙ্ক দুটিকে 4 দ্বারা ভাগ করতে হবে এবং তুল্য স্বর দুটির কম্পাঙ্ক হবে যথাক্রমে \frac{81}{64}f ও \frac{243}{128}f। তাহলে, এখন আমরা কম্পাঙ্কের যে ক্রমটি পেলাম তা হলো:

f(3/2)f(9/8)f(27/16)f(81/64)f(243/128)f2f

যেখানে 2f কম্পাঙ্কটি পরিকল্পিতভাবে স্থাপন করা হয়েছে। এখানে লক্ষণীয় যে, স্বরগুলি কম্পাঙ্কের ক্রমোচ্চ বিন্যাসে সাজানো নেই।  

তৃতীয় ধাপ:

স্বরগুলিকে কম্পাঙ্কের ক্রমোচ্চ বিন্যাসে সাজালে যা পাওয়া যাবে তা হলো:

f(9/8)f(81/64)f(3/2)f(27/16)f(243/128)f2f

চতুর্থ ধাপ:

প্রাথমিক স্বরের মূলকম্পাঙ্ক f থেকে এক পঞ্চম ব্যবধান অবতরণ করলে যে স্বরটি পাওয়া যাবে তার কম্পাঙ্ক হলো \frac{f}{3/2} = \frac{2}{3}f। আমাদের বিবেচ্য অষ্টকের মধ্যে এই স্বরের সমতুল্য স্বরের কম্পাঙ্ক হলো \frac{2}{3}f \times 2 = \frac{4}{3}f। তাহলে শেষপর্যন্ত কম্পাঙ্কের যে বিন্যাস দাঁড়ালো তা নিম্নরূপ:

f(9/8)f(81/64)f(4/3)f(3/2)f(27/16)f(243/128)f2f
(২)

এবার তাহলে স্বরগুলির ব্যবধান বা স্বরান্তরের ক্রমটি দেখা যাক। আগেই বলা হয়েছে যে এই স্বরান্তর মাপা হয় দুটি স্বরের কম্পাঙ্কের অনুপাত দিয়ে। পিথাগোরীয় স্কেলে দুটি ক্রমিক স্বরের কম্পাঙ্কের অনুপাতের ক্রম হলো:

(9/8)(9/8)(256/243)(9/8)(9/8)(9/8)(256/243)

অর্থাৎ এই বিন্যাসে কেবল দুটি পৃথক ব্যবধান আছে: 9/8 এবং 256/243। এখন 9/8 সংখ্যা দ্বারা সূচিত ব্যবধানকে W এবং 256/243 সংখ্যা দ্বারা সূচিত ব্যবধানকে H দিয়ে চিহ্নিত করলে এই স্কেলে ব্যবধানের ক্রমটি হবে WWHWWWH। হারমোনিয়াম বা পিয়ানোর C মেজর স্কেল এই ক্রমবিন্যাসটি মেনে চলে। ২ নং বিন্যাসে প্রদত্ত কম্পাঙ্কগুলিকে আমরা যদি C, D, E, F, G, A, B অর্থাৎ C মেজর স্কেলের স্বরগুলির সাথে সংযুক্ত করি, তাহলে সামঞ্জস্যের চিত্রটি পরিস্ফুট হবে। C থেকে B পর্যন্ত স্বরগুলিকে রোমক সংখ্যা I, II,⋯ দ্বারা ক্রমান্বয়ে চিহ্নিত করলে প্রারম্ভিক স্বরের সাপেক্ষে অন্যান্য স্বরগুলিকে যথাক্রমে Major second, Major third, Perfect fourth, Perfect fifth, Major sixth, Major seventh এবং Octave বলা হয়। হারমোনিয়ামের দুটি সাদা চাবির (reed) মধ্যে একটি কালো চাবি থাকলে সাদা চাবিদুটির ব্যবধানকে W এবং সাদা চাবিদ্বয়ের মধ্যে কোনো কালো চাবি না থাকলে সেক্ষেত্রে ব্যবধানকে H দ্বারা সূচিত করা হয়। যদিও হারমোনিয়াম বা পিয়ানোর চাবিগুলির জন্য এই W ও H গুণকদুটির মান এখানে উল্লিখিত মানের থেকে আলাদা। 

এখন দেখা দরকার এই স্কেল কতখানি যথাযথ। সঙ্গতির বিষয়টি সুনিশ্চিত করতে হলে কোনো স্কেলের স্বরদ্বয়ের ব্যবধানগুলি দুটি ক্ষুদ্র পূর্ণসংখ্যার অনুপাত হওয়া প্রয়োজন। ২ নং বিন্যাস থেকে দেখা যাচ্ছে, চতুর্থ এবং পঞ্চম ভাবের জন্য এই অনুপাত যথাযথভাবে পাওয়া গেলেও অন্যান্য ভাবযুক্ত ব্যবধানগুলি যথাযথ নয়। 

আমরা এই পদ্ধতি অবলম্বন করে আরও কিছুদূর অগ্রসর হতে পারি। প্রাথমিক স্বর থেকে আরম্ভ করে পঞ্চম ভাবযুক্ত স্বর নির্ণয় করার এই প্রক্রিয়াটির পুনরাবৃত্তি ঘটালে কেবলমাত্র H ব্যবধান বিশিষ্ট একটি স্কেল পাওয়া সম্ভব যা ক্রোম্যাটিক স্কেল নামে পরিচিত। এবার তাহলে এই ক্রোম্যাটিক স্কেল গঠনের ধাপগুলি একে একে দেখা যাক।

ক্রোম্যাটিক স্কেল

প্রথম ধাপ:

f মূলকম্পাঙ্ক-বিশিষ্ট প্রাথমিক স্বর থেকে আরম্ভ করে পূর্বোক্ত গুণক দ্বারা পর্যায়ক্রমে ছটি নিম্ন কম্পাঙ্কের স্বর এবং ছটি ঊর্ধ্ব কম্পাঙ্কের স্বর নির্ণয় করলে যে  কম্পাঙ্কগুলি পাওয়া যাবে তা নিচে দেওয়া হলো:

(\frac{2}{3})^6 f(\frac{2}{3})^5 f(\frac{2}{3})^4 f(\frac{2}{3})^3 f(\frac{2}{3})^2 f(\frac{2}{3}) ff(\frac{3}{2}) f(\frac{3}{2})^2 f(\frac{3}{2})^3 f(\frac{3}{2})^4 f(\frac{3}{2})^5 f(\frac{3}{2})^6 f
(\frac{64}{729}) f(\frac{32}{243}) f(\frac{16}{81}) f(\frac{8}{27}) f(\frac{4}{9}) f(\frac{2}{3}) ff(\frac{3}{2}) f(\frac{9}{4}) f(\frac{27}{8}) f(\frac{81}{16}) f(\frac{243}{32}) f(\frac{729}{64}) f

দ্বিতীয় ধাপ:

অষ্টক সমতুল্যতার নীতি কাজে লাগিয়ে 2-এর প্রয়োজনীয় ঘাত গুণ বা ভাগ করে সব স্বরগুলিকে এক অষ্টক ব্যবধানের অন্তর্ভুক্ত করলে প্রাপ্ত বিন্যাসটি হবে:

(\frac{1024}{729}) f(\frac{256}{243}) f(\frac{128}{81}) f(\frac{32}{27}) f(\frac{16}{9}) f(\frac{4}{3}) ff(\frac{3}{2}) f(\frac{9}{8}) f(\frac{27}{16}) f(\frac{81}{64}) f(\frac{243}{128}) f(\frac{729}{512}) f

তৃতীয় ধাপ:

পরবর্তী কাজ হবে স্বরগুলিকে কম্পাঙ্কের ক্রমোচ্চ বিন্যাসে সাজানো:

f(\frac{256}{243}) f(\frac{9}{8}) f(\frac{32}{27}) f(\frac{81}{64}) f(\frac{4}{3}) f((\frac{1024}{729}) f , (\frac{729}{512}) f)(\frac{3}{2}) f(\frac{128}{81}) f(\frac{27}{16}) f(\frac{16}{9}) f(\frac{243}{128}) f2f

বারোটি স্বরবিশিষ্ট ক্রোম্যাটিক স্কেলের ক্ষেত্রে, ত্রয়োদশ স্বরের কম্পাঙ্ক প্রাথমিক স্বরের কম্পাঙ্কের দ্বিগুণ। এখন স্বরব্যবধানগুলি লক্ষ্য করলেই দেখা যাচ্ছে যে, সব ব্যবধানগুলি সমান নয়। যে সমস্যাটি আরও গুরুতর তা হলো, বিন্যাসের কেন্দ্রে একই স্বরের জন্য দুটি পৃথক কম্পাঙ্ক পাওয়া যাচ্ছে— (\frac{1024}{729}) f এবং (\frac{729}{512}) f। আসলে এই স্কেলের বৈশিষ্ট্যসূচক গুণক 3/2-এর দ্বারা কখনোই অষ্টক বদ্ধ করা সম্ভব নয়। কারণ, (\frac{3}{2})^{12} = 129.7463379 যাকে 2-এর ঘাত সহযোগে লিখলে দাঁড়ায় মোটামুটি 1.01364 \times 2^7 অর্থাৎ:

(\frac{3}{2})^{12} = 129.7463379 \approx 1.01364 \times 2^7

তাছাড়া, পিথাগোরীয় স্কেল অনুযায়ী বাঁধা বাদ্যযন্ত্র সেইসব সঙ্গীতের জন্য উপযোগী যেখানে কেবল স্বরের পঞ্চম ব্যবধানের ওপরই গুরুত্ব আরোপ করা হয়। কিন্তু এই স্কেলে কিছু ব্যবধান সঙ্গতিপূর্ণ হলেও বেশিরভাগ ব্যবধানই চরম বিসঙ্গত। এই সমস্যা দূর করার জন্য অন্য একটি স্কেলের উদ্ভাবন হলো যার কথায় এবার আসছি। 

জাস্ট ডায়াটনিক স্কেল        

এক অষ্টকের মধ্যে সাতটি স্বরবিশিষ্ট স্কেলকে বোঝাতে ডায়াটনিক শব্দটি ব্যবহৃত হয়। এই Just scale বা যথাযথ স্কেল প্রাথমিক স্বরের সঙ্গে অন্যান্য স্বরের স্বরকম্প সৃষ্ট বিসম্বাদকে ন্যূনতম করে। এবার এই স্কেলটির গঠন ধাপে ধাপে আলোচনা করা যাক। 

প্রথম ধাপ:

প্রাথমিক স্বর এবং তার সাপেক্ষে তৃতীয় ও পঞ্চম—এই স্বরত্রয় বিবেচনা করা হলো। বিবেচ্য ত্রয়ীর কম্পাঙ্কের অনুপাত 1:5/4:3/2 বা 4:5:6।

4:5:6 আনুপাতিক কম্পাঙ্কের তিনটি স্বরের যুগপৎ ধ্বনি যাকে সঙ্গীতের পরিভাষায় বলা হয় major chord

দ্বিতীয় ধাপ:

f মূলকম্পাঙ্ক-বিশিষ্ট প্রাথমিক স্বর থেকে শুরু করে পর্যায়ক্রমে উচ্চ কম্পাঙ্কের দুটি ত্রয়ী এবং নিম্ন কম্পাঙ্কের একটি ত্রয়ী নির্ণয় করলে নিম্নে প্রদত্ত বিন্যাসটি পাওয়া যাবে।

(2/3) f(5/6) ff(5/4) f(3/2) f(15/8) f(9/8) f
(৩)

৩ নং বিন্যাসের প্রথম তিনটি রাশির অনুপাত 4:5:6। একইভাবে তৃতীয়, চতুর্থ ও পঞ্চম এবং পঞ্চম, ষষ্ঠ ও সপ্তম রাশিত্রয়ের অনুপাতদুটিও 4:5:6। 

তৃতীয় ধাপ:

পরবর্তী কাজ হলো সব স্বরগুলিকে একই অষ্টকের অন্তর্ভুক্ত করা। সেক্ষেত্রে ৩ নং বিন্যাসে প্রদত্ত কম্পাঙ্কগুলির সমতুল কম্পাঙ্ক হবে

(4/3) f(5/3) ff(5/4) f(3/2) f(15/8) f(9/8) f
(৪)

চতুর্থ ধাপ:

এরপর ৪ নং বিন্যাসের কম্পাঙ্কগুলিকে ক্রমোচ্চ বিন্যাসে সাজালে পাওয়া যায়:

f(9/8) f(5/4) f(4/3) f(3/2) f(5/3) f(15/8) f2f
(৫)

তাহলে, ক্রমিক স্বরদ্বয়ের মধ্যে ব্যবধানের ক্রম হলো:

(9/8)(10/9)(16/15)(9/8)(10/9)(9/8)(16/15)
(৬)

৬ নং বিন্যাসে দেখা যাচ্ছে যে, এখানে স্বরান্তরের তিনটি পৃথক মান আছে। আরও গুরুতর সমস্যাটি হলো স্কেল বরাবর একই ভাবযুক্ত স্বরগুলির ব্যবধান সর্বত্র সমান নয়। ৫ নং বিন্যাস অনুযায়ী, প্রারম্ভিক স্বরের সাপেক্ষে পঞ্চম স্বরের কম্পাঙ্ক 3/2 গুণ হলেও দ্বিতীয় ও ষষ্ঠ স্বরের (দ্বিতীয় স্বরের সাপেক্ষে ষষ্ঠ স্বরটিও পঞ্চম্ভাবযুক্ত) ক্ষেত্রে এই অনুপাতটি বজায় রাখা যায়নি, যা পরিবর্তিত স্কেলে সঙ্গীত সৃষ্টির পক্ষে স্কেলটিকে অনুপযোগী করে তুলেছে। অর্থাৎ C এর বদলে D স্বরটিকে টোনিক ধরে সঙ্গীতসৃষ্টি করলে এই অনুপাতগুলো পরিবর্তিত হয়ে যাবে আর স্কেলটি বেসুরো শোনাবে। 

এই সমস্যার সমাধান হিসাবে ইকোয়াল টেম্পার্ড স্কেলের (Equal Tempered scale) অবতারণা।

ইকোয়াল টেম্পার্ড স্কেল

আদর্শ স্কেল আমরা তাকেই বলি যেখানে সমস্ত স্বরান্তর অভিন্ন এবং সঙ্গতির বিচারে প্রত্যেকটি ব্যবধান যথাযথ। কিন্তু দেখা গেছে যে, বারোটি স্বরবিশিষ্ট এমন কোনো স্কেল গঠন করা অসম্ভব যেখানে ইতিপূর্বে বর্ণিত শুভ স্বর-সম্বাদগুলি পাওয়ার জন্য সংশ্লিষ্ট কম্পাঙ্কের অনুপাতগুলি কাঁটায় কাঁটায় রাখা যাবে। অগত্যা, কিছু বিষয়ে আপোষ করা প্রয়োজন। এক্ষেত্রে, বারোটি স্বরবিশিষ্ট অষ্টকের সমস্ত স্বরান্তরগুলি সমান রাখার বিষয়টিকে প্রাধান্য দেওয়া হয়েছে। আমরা যদি এই স্বরান্তরকে a দিয়ে চিহ্নিত করি, তাহলে ত্রয়োদশ স্বরের কম্পাঙ্ক হবে a^{12}f, যেখানে f হলো প্রাথমিক স্বরের কম্পাঙ্ক। আবার স্কেলের সংজ্ঞানুযায়ী, ত্রয়োদশ স্বরের কম্পাঙ্ক প্রাথমিক স্বরের কম্পাঙ্কের দ্বিগুণ। তাহলে:

a^{12}f = 2f অথবা a= 2^\frac{1}{12}

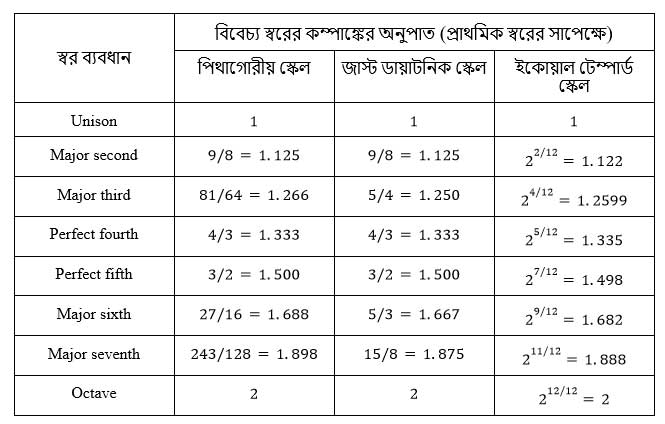
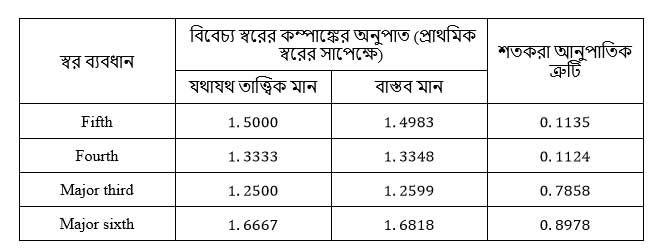
অর্থাৎ, এই স্কেলে পরপর যেকোনো দুটি স্বরের কম্পাঙ্কের অনুপাতটি হলো 2-এর দ্বাদশ মূল। এটি এমন এক সংখ্যা যাকে বারো বার গুণ করলে পাওয়া যায় 2 এবং এর মান মোটামুটি 1.05946। এইভাবে স্কেল গঠন করায় কম্পাঙ্কগুলি যথাযথ হলো না ঠিকই, কিন্তু এতে বিচ্যুতির পরিমাণ এতো কম যে, সাধারণত মানুষের কানে তা ধরা পড়ে না। ১ এবং ২ নং ছকে যথাক্রমে বিভিন্ন স্কেলে স্বরানুপাত ও কয়েকটি ব্যবধানের জন্য ইকোয়াল টেম্পার্ড স্কেলে কম্পাঙ্কগুলির শতকরা ত্রুটির পরিমাণ (যথাযথ মানের সাপেক্ষে) লিপিবদ্ধ করা হয়েছে। ১ নং ছকের ২, ৩ ও ৪ নং স্তম্ভে প্রদত্ত গুণকগুলির দ্বারা প্রাথমিক স্বরের কম্পাঙ্ককে গুণ করলে অন্যান্য স্বরের কম্পাঙ্ক পাওয়া যায়।

১ নং ছক: বিভিন্ন স্কেলে স্বরসমূহের কম্পাঙ্কের অনুপাত (প্রাথমিক স্বরের সাপেক্ষে)
২ নং ছক: ইকোয়াল টেম্পার্ড স্কেলে নির্বাচিত স্বরসমূহের কম্পাঙ্কের অনুপাত (প্রাথমিক স্বরের সাপেক্ষে) ও যথাযথ মানের সাপেক্ষে শতকরা ত্রুটি 

আধুনিক পাশ্চাত্য সংগীত

আধুনিক পাশ্চাত্য সঙ্গীত অর্কেস্ট্রেশন-প্রধান। অর্থাৎ অনেক বাদ্যযন্ত্র ও কন্ঠ একইসাথে নানা স্বরে বাজলে তাদের সমন্বয়ের (harmony) যে রস, তাকেই প্রধান গুরুত্ব দেওয়া হয়। ঐকবাদনের ক্ষেত্রে সুসমন্বয়সাধন বা orchestration এর প্রয়োজনে পিয়ানোর (ইকোয়াল টেম্পার্ড স্কেলে বাঁধা) চতুর্থ অক্টেভের A চাবির কম্পাঙ্ক বাঁধা হয়েছে 440 হার্ৎসে। সঙ্গীত পরিবেশনের মাঝে ইকোয়াল টেম্পার্ড স্কেলে টোনিক পরিবর্তন খুব সহজ, যেহেতু সবকটি স্বর সমান আনুপাতিক দূরত্বে অবস্থিত। এই সব কারণে আধুনিক পাশ্চাত্য সঙ্গীতে ইকোয়াল টেম্পার্ড স্কেল খুব জনপ্রিয়। যদিও অনেক সঙ্গীতস্রষ্টা এর পাশাপাশি অন্যান্য স্কেল নিয়েও নিরন্তর পরীক্ষানিরীক্ষা করে চলেছেন।

ভারতীয় সঙ্গীতের স্কেল বা ঠাটের তত্ত্ব নিয়ে আমরা পরের পর্বে বিশদে আলোচনা করবো।  

কৃতজ্ঞতা স্বীকার 

অধ্যাপক পলাশ বরন পাল পাণ্ডুলিপিটি খুঁটিয়ে পড়ে অনেক ভুলভ্রান্তি সংশোধন করে দিয়েছেন। নিরন্তর উৎসাহ জুগিয়েছেন অধ্যাপক নিখিল চক্রবর্তী এবং স্কটিশ চার্চ কলেজের পদার্থবিদ্যা বিভাগের সদস্যরা। এছাড়াও বিজ্ঞান পত্রিকার সম্পাদকমণ্ডলীর পরামর্শ ও সহায়তা লেখাটার মানোন্নয়নে বিশেষভাবে সহায়ক হয়েছে। 

প্রচ্ছদের ছবি: PixaBay

তথ্যসূত্র 

১. Good Vibrations: The Physics of Music, Barry Parker, The Johns Hopkins University Press (2009).

২. The physics of musical scales: Theory and experiment, Dallin S. Durfee and John S. Colton, American Journal of Physics 83, 835 (2015).

৩. Music: A Mathematical Offering, Dave Benson, Cambridge University Press (2006).    


৪.

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/science-of-music-western-01

print