কোয়ান্টাম কম্পিউটিং: ব্যাপারখানা কী! (২)

ওমর শেহাব

(IonQ)

 

16 Mar 2018

Link: https://bigyan.org.in/quantum-computing-2

এই লেখাটি পড়ার জন্য পাঠকদের যেসব জিনিস জানা থাকলে সুবিধা হবে সেগুলি হল: বীজগণিত ও বাইনারী বা দ্বিমিক সংখ্যা ব্যবস্থা। নিউটনের সূত্র ও কোয়ান্টাম মেকানিক্স জানা থাকলে সুবিধে, কিন্তু জানা না থাকলেও সমস্যা নেই।

প্রথম পর্বে আলোচিত হয়েছিল কম্প্যুটিং-এর সংক্ষিপ্ত ইতিহাস। হিলবার্টের দশম সমস্যার উত্তর খুঁজতে গিয়ে কম্পিউটার বিজ্ঞান আর তার মৌলিক গাণিতিক ভিত্তি ট্যুরিং যন্ত্রের জন্ম।

দ্বিতীয় পর্ব

অচেনা কোয়ান্টাম জগৎ

বিংশ শতাব্দীর শুরুতে বিজ্ঞানে ঘটে গেল যুগান্তর। এতদিনের চেনা জানা বিজ্ঞান, যেমন নিউটনের বলবিদ্যা বা আলোক বিজ্ঞান, কিছু প্রাকৃতিক ঘটনা ব্যাখ্যা করতে গিয়ে হুড়মুড়িয়ে পড়ল। আলো এবং পদার্থের ক্ষুদ্রাতিক্ষুদ্র কণিকার স্বরূপ বুঝতে দরকার পড়ল এক নতুন চিন্তাভাবনার – যার নাম হল কোয়ান্টাম বলবিদ্যা। আলোকে এতদিন আমরা তরঙ্গ বলে ভাবতাম, দেখা গেল সে কণিকার মত হয়ে যাচ্ছে কখনো! আবার যাকে এতদিন কণা বলে ভাবতাম, যেমন অণু-পরমাণু-ইলেকট্রন ইত্যাদি, তারা আলোর তরঙ্গের মত করেই এক জায়গা থেকে আরেক জায়গা ছুটে চলছে! আমাদের চেনা জগতের মূলে রয়েছে এক বিস্ময়কর অচেনা জগৎ, যেখানে এই কণা ও তরঙ্গের হিসেবটা গুলিয়ে যায়। ম্যাক্স প্লাঙ্ক, নীলস বোর, শ্রডিংগার, হাইজেনবার্গ, ডি ব্রইলি, আইনস্টাইন ইত্যাদি বিজ্ঞানীরা এই রহস্যময় জগতের চাবিকাঠি বের করা শুরু করলেন। ক্ল্যাসিক্যাল পদার্থবিদ্যা, যার মধ্যে নিউটন, ম্যাক্সওয়েল ইত্যাদি বিজ্ঞানীর আবিষ্কার ছিল, তাকে ফেলে দিতে হল না, কিন্তু বোঝা গেল কোয়ান্টাম বলবিদ্যার সাহায্য ছাড়া শুধু ক্ল্যাসিক্যাল পদার্থবিদ্যা দিয়ে জগত ব্যাখ্যা করা সম্ভব নয়। কোয়ান্টাম জগতের কথা পূর্ব প্রকাশিত এই লেখাটিতে পড়ে দেখতে পারেন।

কম্পিউটারের সাথে কোয়ান্টামের সম্পর্ক কোথায়? ফাস্ট ফরওয়ার্ড করে বিংশ শতাব্দীর শুরু থেকে শেষের দিকে চলে যাওয়া যাক এই গল্পটা শুনতে!

ফাইনম্যানের বুদ্ধি

আপনাদের নিয়ে যাব আশির দশকের শুরুতে। নোবেল বিজয়ী পদার্থবিজ্ঞানী রিচার্ড ফাইনম্যান প্রকাশ করলেন পর পর দুটি প্রবন্ধ – ঊনিশশো বিরাশি সালে ‘সিমুলেটিং ফিজিক্স উইথ কম্পিউটার’ ও ঊনিশশো পঁচাশি সালে ‘কোয়ান্টাম মেকানিক্যাল কম্পিউটারস’।

ততদিনে বিজ্ঞানীরা জানেন, ছোটখাট কোয়ান্টামতন্ত্রের¹ সিমুলেশনও² কম্পিউটারে করা ভারী কঠিন ব্যাপার।

কম্পিউটার আবিষ্কার হওয়ার পর প্রথমদিকে এটি ব্যবহার করতেন কেবল বিজ্ঞানী ও গণিতবিদরা। পদার্থবিজ্ঞানীরা যেসব কাজে ব্যবহার করা শুরু করলেন তার মধ্যে একটি হল ছোটখাট কোয়ান্টামতন্ত্রের সিমুলেশন বা মহড়া। যেমন ধরা যাক দশটি পানির অণু। প্রতিটি অণুর মধ্যে আছে হাইড্রোজেনের দুটি পরমাণু আর অক্সিজেনের একটি পরমাণু। কেউ যদি জানতে চায় কখন এই দশটি অণুর দলটি বরফ, পানি বা জলীয় বাষ্প হিসেবে থাকবে আমরা কি করে বলব? এটি নির্ভর করে তাদের বিভব শক্তি ও গতি শক্তির উপর। সেটি কিসের উপর নির্ভর করে? প্রতিটি অণুর ভিতরে পরমাণুগুলোর যে রাসায়নিক বন্ধন, কম্পন, আর গতিশক্তি তার উপর। বরফের চেয়ে জলীয় বাষ্পে হাত দিলে গরম বেশি লাগে কেন? কারণ জলীয় বাষ্পের অণুগুলোর গতিশক্তি অনেক বেশি।

অনেকে বলতে পারেন যে দশটি অণুর প্রতিটিতে তিনটি কণা। কাজেই আমরা মোট ত্রিশটি কণা নিয়ে নিউটনের গতিসূত্রে ফেলে দিলেই তো কাজ হয়, কোয়ান্টাম মেকানিক্সের কি দরকার? দরকার কারণ নিউটনের গতিসূত্রে ফেলে দিলে যে তাপমাত্রায় পানির দশা পরিবর্তন দেখবে বাস্তবে তার চেয়ে ভিন্ন তাপমাত্রায় ঘটে (২০০৬ সালে লেখা উইক এবং স্কেন্টারের একটি গবেষণাপত্রে পানির স্ফুটনাঙ্কে প্রায় ১৭ কেলভিন পার্থক্য পাওয়া গেছে)। তাহলে আমাদের আরো নিখুঁত পদার্থবিদ্যার নীতির প্রয়োজন হবে। সেটি হল কোয়ান্টাম মেকানিক্স।

সমস্যা শুধু এই নয় যে আশির দশকে কম্পিউটারগুলো দুর্বল ছিল। সে তো ছিলই। কিন্তু মূল সমস‌্যা আরো গভীরে। কোয়ান্টামতন্ত্রগুলির মহড়া চালানোর কাজটি এত জটিল যে কম্পিউটার আধুনিক হলেও খুব বেশি আগানো যায় না। এই জটিলতার মূল কারণ হল যে কোয়ান্টাম কণা তরঙ্গের মত একসাথে অনেক জায়গায় থাকতে পারে, তাই তাকে বর্ণনা করতে দরকার বিভিন্ন জায়গায় তাকে পাওয়ার সম্ভাব্যতার হিসেবনিকেশ। এই সম্ভাব্যতার হিসেব করার জন্য প্রয়োজন বিষমসূচক সমীকরণ বা ডিফারেন্সিয়াল সমীকরণ আর জটিল সংখ্যাতন্ত্র (complex numbers)। গণিতের এই শাখার সমস্যাগুলো যান্ত্রিক উপায়ে সমাধান করতে চাইলে অনেক সময় লাগে। এখনকার সবচেয়ে শক্তিশালী সুপারকম্পিটারেও পঞ্চাশটি বা তার বেশি কণা বিশিষ্ট কোয়ান্টামতন্ত্রের মহড়া দেয়া অনেক সময়ই সম্ভব না। কণা যত বেশি সেই কোয়ান্টামতন্ত্রের সিমুলেশনও তত বড় কাজ।

ফাইনম্যান ঠিক এখানেই নতুন একটি প্রস্তাব নিয়ে আসলেন। উনি বললেন, মানলাম আমাদের প্রথাগত বা ধ্রুপদী কম্পিউটার কোয়ান্টাম কণার মহড়া দিতে সুবিধে করতে পারবে না। কিন্তু কম্পিউটারটি নিজেই যদি কোয়ান্টাম মেকানিক্সের নীতি অনুসরণ করে চলে তাহলে কি লাভ হবে? ফাইনম্যান কিছু ধারণা দিলেন কম্পিউটারের মৌলিক কাজগুলো কি করে কোয়ান্টাম মেকানিক্স দিয়ে করা যায়।

কোয়ান্টাম ও ট্যুরিং যন্ত্র

কোয়ান্টাম মেকানিক্সের নীতির ভিত্তিতে ট্যুরিং যন্ত্রে কি পরিবর্তন আনতে হবে?
পাঠকদেরকে ‘কিউবিট’ কথাটির সাথে পরিচয় করিয়ে দেওয়ার এখন উপযুক্ত সময়। ধ্রুপদী কম্পিউটারে কি পরিমাণ তথ্য সংরক্ষণ করা যায় সেটি মাপা হয় বিট দিয়ে। একটি বিট ০ আর ১ – এই দুই অবস্থায় থাকতে পারে। কোয়ান্টাম কম্পিউটারে সেটির কাছাকাছি ধারণা হল কিউবিট। বিটের সাথে এর তফাৎ হল যে কিউবিট ০ আর ১ – এই দুটো অবস্থার যে কোন সুপারপোজিশান বা উপরিপাতন অবস্থায় থাকতে পারে। সুপারপোজিশান অবস্থা মানে একই সাথে তার ০-তে থাকার কিছু সম্ভাবনা আছে, আবার ১-এ থাকার কিছু সম্ভাবনা আছে। এই ধরণের সুপারপোজিশান কোয়ান্টাম মেকানিক্সের মূলে আছে, এবং ক্ল্যাসিক্যাল বা ধ্রুপদী জগতের সাথে কোয়ান্টামের তফাৎ এখানেই। ধ্রুপদী ট্যুরিং যন্ত্রের টেপে ১ আর ০ চিহ্ন দুটি লেখা হয়। কোয়ান্টাম বলবিদ্যা মেনে চলে এমন কণা দিয়ে একটি কোয়ান্টাম ট্যুরিং যন্ত্র বানানো হলে সেটির ‘টেপ’ ১ আর ০ এর উপরিপাতনে থাকতে পারবে।

ধ্রুপদী ট্যুরিং ও কোয়ান্টাম ট্যুরিং যন্ত্রের আরেকটি তফাৎ হল যে কোয়ান্টাম ট্যুরিং যন্ত্রের কোন পরিবর্তন প্রত্যাহার যোগ্য (reversible) হতে হবে। যেমন, ধ্রুপদী ট্যুরিং যন্ত্রের উদাহরণে আমরা ২ আর ৩ যোগ করে ৫ বের করেছিলাম। একবার ৫ বের করে ফেলার পর কিন্তু আর টেপটি দেখে বলার কোন উপায় নেই এটি ২ + ৩ থেকে এসেছে নাকি ১ + ৪ থেকে এসেছে। অর্থাৎ, এই পরিবর্তনটি প্রত্যাহারযোগ্য নয়। কোয়ান্টাম ট্যুরিং যন্ত্রে এইধরণের পরিবর্তন করা যাবে না। আমাদের শুধু যোগ করলে হবে না, কি কি যোগ করা হয়েছে সেই ইতিহাসটিও কোনভাবে রেখে দিতে হবে। একটি উপায় হতে পারে ২ আর ৩ এমন ভাবে যোগ করা যাতে ৩ এর জায়গায় যোগফল ৫ লেখা হয় কিন্তু ২ মুছে না যায়। তাহলে কেউ অন্য সংখ্যাটি জানতে চাইলে ৫ থেকে ২ বিয়োগ করেই পেয়ে যাবে। এ ধরণের ট‌্যুরিং যন্ত্র আমরা কি করে বানাবো? তখন আর বুলিয়ান বীজগণিতে আমাদের কাজ হবে না। আমাদের রৈখিক বীজগণিতকে ভিত্তি ধরে এগুতে হবে। কেন? (২, ৩) → (২, ৫) এই গাণিতিক প্রক্রিয়াটিকে বিন্যাসের ভাষায় খুব সহজে প্রকাশ করা যায়। আর বিন্যাসের বীজগণিতটি রৈখিক বীজগণিত দিয়ে খুব সহজে প্রকাশ করা যায়।

এখন আমাদের দরকার কোয়ান্টাম কম্পিউটার বিজ্ঞানের গাণিতিক ভিত্তি যেটি ধ্রুপদী কম্পিউটার বিজ্ঞানের জন্য অ্যালান ট্যুরিং তৈরি করেছিলেন। কেন দরকার এই ভিত্তি? দুটি কারণ বলতে পারি। প্রথমটি হল এই গাণিতিক ভিত্তি আমাদের কম্পিউটার বিজ্ঞানের সূক্ষ্মাতিসূক্ষ্ম বিষয় পরিষ্কারভাবে বর্ণনা করার ভাষা দেয়। দ্বিতীয়ত: এই গাণিতিক ভিত্তি আমাদেরকে কম্পিউটার অ্যালগরিদমের গুণগত মান পরিমাপের কাঠামো ও মাণদন্ড দেয়। গুণগত মান বলতে অ্যালগরিদমটি কত তাড়াতাড়ি কাজ শেষ করে, কী পরিমাণ তথ্য সংরক্ষণের জায়গা খরচ করে আর ফলাফল কতটুকু নিখুঁত এসব বোঝায়।

একটি উদাহরণ দেই। আমাদের দৈনন্দিন জীবনে নানা প্রয়োজনীয় জিনিস কেনার জন্য মুদি দোকানে যেতে হয়। মুদি দোকানে ঠিক জিনিস ঠিক পরিমাণে কেনা যেমন গুরুত্বপূর্ণ, কেনার পর লেনদেন নিখুঁত হয়েছে কিনা সেটি যাচাইও সমান গুরুত্বপূর্ণ। শুধু তাইই নয়, যদি একাধিক মুদি দোকান থাকে তাহলে কোন দোকানে কি কিনলে পকেটের টাকার সর্বোত্তম ব্যবহার হবে সেটি জানাও জরুরি। এসব কিছু ঠিকঠাক মত করার জন্য একটি সুন্দর গাণিতিক ভাষা ও ভিত্তি থাকা উচিৎ। সেটি কি? পাটিগণিত!

কোয়ান্টাম কম্পিউটিঙের গাণিতিক ভিত্তি

কোয়ান্টাম কম্পিউটিংয়ের জন্য সেই গাণিতিক ভিত্তি অর্থাৎ অ্যালান ট্যুরিঙের তত্ত্বের কোয়ান্টাম সংস্করণ এল ঊনিশশো পঁচাশি সালে ডেভিড ডয়েচের গবেষণাপত্রে।
ডেভিড ডয়েচ ট্যুরিং মেশিনের বর্ণনা একটু পরিবর্তন করে সেখানে কোয়ান্টাম বলবিদ্যা ঢুকিয়ে দিলেন। আগে বলেছি প্রোগ্রাম বা নির্দেশমালার বর্ণনা লেখার জন্য ‘০’ আর ‘১’ এই চিহ্ন দুটি ব্যবহার করা হত। কোয়ান্টাম বলবিদ্যার ধারণা ব্যবহার করে ডয়েচ প্রস্তাব করলেন ‘০’ আর ‘১’ এর উপরিপাতন বা সুপারপজিশন ব্যবহার করে প্রোগ্রামের বর্ণনা লিখতে। তার সাথে আরো কিছু পরিবর্তন করে তিনি কোয়ান্টাম ট্যুরিং যন্ত্রের ধারণাটি দাঁড় করালেন।

এখন আমাদের দেখতে হবে এই নতুন ধরণের কম্পিউটিং দিয়ে এমন কোন কাজ করা যায় কিনা যেটি ধ্রুপদী কম্পিউটিংয়ে করা যায় না। যদি কোন কাজ এই নতুন ধরনের কম্পিউটিংয়ে ধ্রুপদী কম্পিউটিংয়ের চেয়ে কম খরচে (কম সময়, কম তথ্য সংরক্ষণ, কম বিদ্যুৎ খরচ ইত্যাদি) করা যায় তাহলেও চলবে!

প্রথম কোয়ান্টাম ধারাক্রম বা অ্যালগরিদম

কোয়ান্টাম কম্পিউটিং দিয়ে ধ্রুপদী কম্পিউটিংয়ের চেয়ে বেশি কিছু করা যায় কিনা সেই প্রশ্নের উত্তরও আমরা পেলাম একই বছর – ডয়েচের অ্যালগরিদম। কি করে সেই অ্যালগরিদম? কি সেই কাজ?

কল্পনা করুন, আপনার কাছে একটি যন্ত্র আছে – দেখতে সব দিক দিয়ে বন্ধ একটি বাক্স। কেবল সামনে একটি ফুটো এবং পেছনে আরেকটি। কি কাজ করে এই বাক্স? প্রথম ফুটো দিয়ে এটি কেবল একটি রঙিন কাচের গোলক ভেতরে নেয় আর ভেতরে গোলকটিকে রং করে সামনের ফুটো দিয়ে বের করে দেয়। এই রঙেরও কিছু খুঁটিনাটি নিয়ম আছে। বাক্সটি কেবল লাল বা নীল রঙের গোলক ভেতরে নেয়। যেহেতু আমরা এই বাক্সটি বানাতে যাচ্ছি না কাজেই কি করে এই সব শর্ত নিশ্চিত করব এই আলোচনার জন্য সেটি গুরুত্বপূর্ণ নয়। এটি একটি কাল্পনিক পরীক্ষা। বাক্সটি গোলকটি ভেতরে নেয়ার পর হয় এটিকে লাল বা নীল রঙ করে সামনের ফুটো দিয়ে বের করে দেয়।

আমরা কেবল বাক্সের বর্ণনা শেষ করলাম। এখন কী সমস্যা আমরা সমাধান করতে যাচ্ছি?

একটা ব্যাপার খেয়াল করুন। উপরের বর্ণনা অনুযায়ী আমরা বড়জোর চার ধরণের যন্ত্রের কথা ভাবতে পারি। প্রথম দুটিকে আমরা বলতে পারি সুষম যন্ত্র। প্রথম সুষম যন্ত্রটিতে যে রঙের গোলক ঢুকবে যন্ত্রটি সেই রঙই আবার গোলকের উপর দিয়ে বের করে দিবে। অর্থাৎ লাল গোলক ঢুকলে লাল গোলক বের হবে, নীল গোলক ঢুকলে নীল। দ্বিতীয় সুষম যন্ত্রটি এমন হবে যেখানে বিপরীত রঙটি গোলকের উপর দেয়া হবে। অর্থাৎ লাল গোলক ঢুকলে নীল গোলক বের হবে আর নীল ঢুকলে লাল।

এছাড়া দুটি বিষম যন্ত্রও আমরা কল্পনা করতে পারি। প্রথম বিষম যন্ত্রটি যেই গোলকই ঢুকুক না কেন তার উপর নীল রঙ দিয়ে দিবে আর দ্বিতীয় বিষম যন্ত্রটি যেই গোলকই ঢুকুক না কেন তার উপর লাল রঙ দিয়ে দিবে।

সব বাক্সই বাইরে থেকে দেখতে একই রকম – কাল রঙের। এখন আপনাকে যদি একটি বাক্স দেয়া হয়, আপনি কি করে বলবেন এটি সুষম নাকি বিষম যন্ত্র?

কাজটি খুব বেশি কঠিন না। আপনি দুটি ভিন্ন রঙের বল নিবেন – লাল আর নীল। যদি দুটি বলই একই রঙ নিয়ে বাক্স থেকে বের হয় তাহলে বিষম আর ভিন্ন রঙ নিয়ে বের হয় তাহলে সুষম। এর অর্থ হল যন্ত্রটি দুবার ব্যবহার করতে পারলে আপনি বলতে পারবেন সেটি কোন ধরণের।

এই সহজ কাজটি ডেভিড ডয়েচ আরো সহজে করলেন কোয়ান্টাম কম্পিউটিং ব্যবহার করে। এটিই ইতিহাসের প্রথম কোয়ান্টাম অ্যালগরিদম – পাঠ্যবইয়ে ডয়েচের অ্যালগরিদম হিসেবে পাবেন।

কীভাবে সেটি কাজ করে? একদম খুলে বলতে গেলে কয়েকপাতা লেগে যাবে। অল্প জায়গায় যতটুকু পারি বলার চেষ্টা করি।

ডেভিড ডয়েচ কী করলেন, বাক্সটিতে লাল গোলক বা নীল গোলক পাঠালেন না! তিনি পাঠালেন লাল ও নীল গোলকের উপরিপাতন! যারা আমার জন্য পাগলা গারদের ডিসকাউন্টের খোঁজ শুরু করে দিয়েছেন তাদের অনুরোধ করছি আরেকটু ধৈর্য ধরার জন্য! তাহলে বাক্সটিতে যে গোলকটি ঢুকল সেটি একই সাথে লাল ও নীল। এখন এটি যদি প্রথম সুষম যন্ত্রটি হয় তাহলে সেটি লালকে লাল আর নীলকে নীল রঙ দিবে অর্থাৎ যে গোলকটি বের হবে সেটি হবে লাল ও নীল গোলকের উপরিপাতন। যদি দ্বিতীয় সুষম যন্ত্র হয় যেটি লালকে নীল আর নীলকে লাল রঙ দিবে তাহলেও যে গোলকটি বের হবে সেটি হবে লাল ও নীল গোলকের উপরিপাতন।

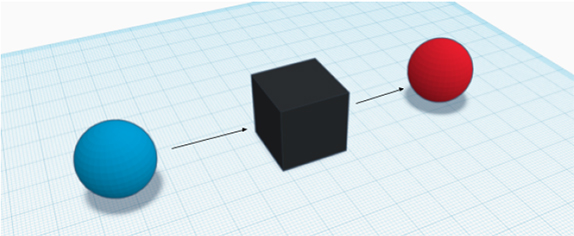
বিষম যন্ত্র হলে কি হবে? প্রথম বিষম যন্ত্রে যে রঙই আসুক না কেন তার উপর নীল রঙ দিয়ে দিবে। কাজেই যে গোলকটি বের হবে সেটি হবে নীল ও নীল রঙের গোলকের উপরিপাতন। তার মানে বের হবে নীল গোলক। একই ভাবে দ্বিতীয় বিষম যন্ত্র থেকে বের হবে লাল গোলক।

আপনারা কি ইতিমধ্যে একটি ব্যাপার খেয়াল করেছেন? যদি কোন গোলক উপরিপাতনে থাকে তাহলে একাধিক কাজ সমান্তরালে করা যায়। দ্বিতীয় সুষম যন্ত্রের কথাটি আবার মনে করুন। যেই গোলকই আসুক না কেন তার বিপরীত রং দেয়া হবে। কাজেই যদি গোলকটি নীল ও লাল রঙের উপরিপাতন হয় তাহলে একই সাথে সেটি লাল (নীল গোলককে) ও নীল (লাল গোলককে) রঙ দিবে। এর অর্থ হল যতক্ষণ পর্যন্ত আমরা উপরিপাতন বজায় রাখছি ততক্ষণ পর্যন্ত আমরা একাধিক কাজ সমান্তরালে করতে পারব।

ডেভিড ডয়েচ ঠিক এই বুদ্ধিটিই কাজে লাগালেন। তিনি দু’ধরণের রঙ করার ও যাচাইয়ের কাজ সব কিছুই করলেন উপরিপাতনে অর্থাৎ সমান্তরালে। তাই, ধ্রুপদী কম্পিউটার বিজ্ঞানে যেখানে দু’বার যন্ত্রটি ব্যবহার করতে হয় সুষমতা বা বিষমতা বের করার জন্য, ডয়েচ সেখানে যন্ত্রটি ব্যবহার করলেন মাত্র একবার। অর্থাৎ কাজের পরিমাণ তিনি অর্ধেকে নিয়ে আসলেন। যেকোন কোয়ান্টাম কম্পিউটারে যখন ফলাফল বের করা হয় তখন কিভাবে তথ্যটি পড়া হচ্ছে এটি খুব গুরুত্বপূূর্ণ। কাজেই আমাদের এই উদাহরণের ক্ষেত্রে সবশেষে কিভাবে ফলাফলটি পড়া হবে সেটি কিছু সুনির্দিষ্ট নিয়ম আছে। সেটির বিস্তারিত বর্ণনা অন্য কোথাও দেয়া যাবে।

ধাঁধাটি বাস্তব জীবনে হয়তো কোন কাজে লাগেনা কিন্তু সেটিও আমরা কোয়ান্টাম কম্পিউটিং দিয়ে সমাধান করলাম ধ্রুপদী কম্পিউটার বিজ্ঞানের চেয়ে আরো কম খরচে।

টীকা

1. কোয়ান্টামতন্ত্র বা কোয়ান্টাম সিস্টেম হল এমন একটি বস্তু যার ধর্ম কোয়ান্টাম বলবিদ্যা ছাড়া ব্যাখ্যা করা সম্ভব নয়। এর একটি উদাহরণ হল পানির অণু। পানির অণুর বিভিন্ন ধর্ম নিউটনীয় বলবিদ্যা দিয়ে ব্যাখ্যা করা যায় না। এর জন‌্য প্রয়োজন কোয়ান্টাম বলবিদ্যা।
2. কম্পিউটার সিমুলেশন বা কম্পিউটারের মহড়া বস্তুর ধর্ম সম্পর্কে জানার জন্য খুবই সস্তা পদ্ধতি। অনেক পদার্থ আছে যেগুলো নিয়ে পদার্থবিদ্যা বা রসায়ন গবেষণাগারে কাজ করা কঠিন বা ঝুঁকিপূর্ণ। কখনও কখনও আবার কেবল দামের জন্য সবসময় সেগুলো নিয়ে সবাই গবেষণাগারে কাজ করতে পারে না। কম্পিউটার মহড়ার মাধ্যমে গাণিতিক মডেল বা গাণিতিক আদল তৈরি করা হয় যে পদার্থটির অনেক ধর্মই ধারণ করে। এর পর বিভিন্ন প্রাথমিক শর্তের জন্য (যেমন উচ্চ তাপমাত্রা অথবা অন্য আরেকটি বিক্রিয়কের উপস্থিতি) গাণিতিক আদলটি ব্যবহার করে পদার্থটির বিভিন্ন ধরনের আচরণ পর্যবেক্ষণ করা হয়।

(চলবে)

উৎসর্গ: মুক্তচিন্তক শহীদ অভিজিৎ রায়
কৃতজ্ঞতা: মাহবুব আজাদ আজাদকে পরিভাষা ও বানানের ব্যাপারে সাহায্যের জন্য ধন্যবাদ।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/quantum-computing-2

print