21-12-2024 17:04:10 pm

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

সাইজের মাহাত্ম্য — প্রকৃতি থেকে প্রযুক্তিতে

কৌশিক দাস

(U Maryland, Eastern Shore)

ল্যারি গণিক

(Cartoonist)

07 Oct 2022

Link: https://bigyan.org.in/on-being-the-right-size-02

%e0%a6%b8%e0%a6%be%e0%a6%87%e0%a6%9c%e0%a7%87%e0%a6%b0-%e0%a6%ae%e0%a6%be%e0%a6%b9%e0%a6%be%e0%a6%a4%e0%a7%8d%e0%a6%ae%e0%a7%8d%e0%a6%af-%e2%80%94-%e0%a6%aa%e0%a7%8d%e0%a6%b0%e0%a6%95%e0%a7%83

প্রকৃতিতে অনেক ঘটনা কোনো একটা পৃষ্ঠতলের (surface) মধ্যে দিয়ে ঘটে। যেমন, খাদ্য কিম্বা অক্সিজেন শোষণ। তাই, সাইজে বেড়ে গেলে সেই অনুপাতে পৃষ্ঠতলও বাড়াতে হয়। পৃষ্ঠতল বাড়ানোর অনেকরকম ফন্দি প্রকৃতি ভেবে রেখেছে। এখন, সেইসব ফন্দি প্রযুক্তির জগতেও কাজে লাগছে।

প্রাণীজগতের বৈচিত্র অসাধারণ। ক্ষুদ্র কীটপতঙ্গ থেকে শুরু করে বৃহদাকার হাতি বা তিমির মতো প্রাণী, সবই রয়েছে তাতে।

এরকম একেবারেই নয় যে সাইজ যত বাড়ে, একই প্রাণী দৈর্ঘ্যে প্রস্থে উচ্চতায় বেড়ে যায়। সাইজ পাল্টালে প্রাণীর চেহারাছবিও পাল্টায়। হাতির সাইজের হরিণ বা ঘটোৎকচের সাইজের মানুষ আমরা কখনোই দেখতে পাই না। পাল্টায় ক্ষমতাও। আমরা পুকুরে বা নদীতে ডুব দিয়ে স্নান করে অনায়াসে পাড়ে উঠে আসতে পারি। কিন্তু একটা মাছি বা পতঙ্গ জলে ভিজে গেলে সেখান থেকে আর বেরিয়ে আসতে পারে না, তার মৃত্যু অনিবার্য।

শুধু বাহ্যিক শারীরিক গঠন বা আচার-আচরণ নয়, বিভিন্ন সাইজের প্রাণীগুলোর অভ্যন্তরীণ গঠনও আলাদা। একটা কেঁচোর পাচনতন্ত্র খুব সাধারণ — একটা সোজা নল যার মাধ্যমে সে জীবন ধারণের জন্য প্রয়োজনীয় খাদ্য শুষে নিতে পারে। কিন্তু সেই কেঁচোর সাইজের একশো দুশো গুন্ বড় প্রাণী হলে পাক প্রণালীটা আর সোজাসাপ্টা থাকেনা। যেমন মানুষ। মানুষ এবং সমগোত্রের প্রাণীদের অন্ত্র জটিল এবং প্যাঁচালো, মোটেই কেঁচোর মত সাধারণ সোজা নল নয়!

কেন এমন হয়? এই ধরণের আপাত সংযোগবিহীন ঘটনাগুলির মধ্যে কি কোন অন্তর্নিহিত সাদৃশ্য কাজ করে? বিজ্ঞান পত্রিকায় প্রকাশিত সাইজ এর মাহাত্ম্য লেখাটিতে এই বিষয়গুলি নিয়েই আলোচনা করা হয়েছে। আমরা দেখেছি কিভাবে একটা প্রাণীর শরীরের পৃষ্ঠতলের (surface area) ও আয়তনের (volume) অনুপাত, অথবা শরীরের প্রস্থচ্ছেদ (cross-sectional area) ও ওজনের (weight) অনুপাত আপাত জটিল বিবর্তনের কিছুটা হলেও দিগনির্দেশ করতে পারে।

শুধুমাত্র প্রাকৃতিক বিবর্তনই নয়, এই পৃষ্ঠতল ও আয়তনের অনুপাত প্রযুক্তির বিবর্তনকেও প্রভাবিত করতে পারে। আধুনিক ক্যাপাসিটরে (supercapacitor) কম উপাদান ব্যবহার করে অনেক চার্জ ধারণ করা যায়, বা তাপ পরিবহনের জন্য ন্যানোকণার ব্যবহার করে কম আয়তনের উপাদানে অনেক বেশি পৃষ্ঠতল তৈরী করা সম্ভব হয়।

তাই, কোন বস্তুর পৃষ্ঠতলের ক্ষেত্রফল বা প্রস্থচ্ছেদের পরিমাপ তার আয়তনের অনুপাতের উপর কিভাবে নির্ভর করে, সেটা জানা অত্যন্ত গুরুত্বপূর্ণ। এই কারণেই আমরা নিচের কার্টুন প্রশ্নমালা তৈরী করেছি। আশা করা যায়, প্রশ্নগুলোর উত্তর দিতে দিতে ধাপে ধাপে প্রাকৃতিক থেকে প্রযুক্তির বিবর্তনের গতিপথ কিছুটা হলেও অনুধাবন করতে পারবে।

[১]

অনিতা হঠাৎ করে একটা চিনির ঘনক (cube) পেল যেটার একটা বাহুর দৈর্ঘ্য 1 m। সে খুব সাবধানে চিনির বড় ঘনকটাকে কেটে কয়েকটা ছোটো ছোটো ঘনক তৈরী করলো। ধরে নাও, অনিতা লোভে পড়ে চিনির টুকরো খেয়ে ফেলেনি।

Loading ...

[২]

অনিতা তার 1 m বাহু চিনির ঘনকটাকে এমনভাবে কাটলো যাতে ঐ ছোটো ছোটো খণ্ডগুলো 10 cm বাহুর ঘনক হয়। বড় ঘনকটার পৃষ্ঠতলীয় ক্ষেত্রফলের (surface area) তুলনায় এই ছোটো ছোটো ঘনকগুলির সম্মিলিত পৃষ্ঠতলীয় ক্ষেত্রফল কত বেশি বা কম হবে?

1000 গুণ বেশি
100 গুণ বেশি
10 গুণ বেশি
1/10 গুণ
একই

[৩]

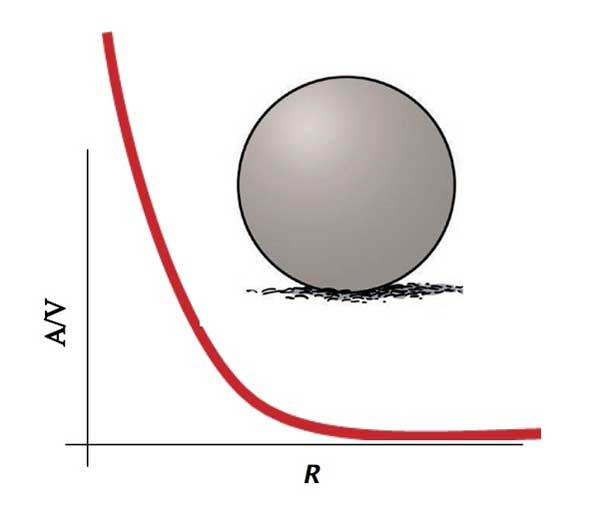
R ব্যাসার্ধের একটা লোহার গোলককে মাত্র কয়েক ন্যানোমিটার ব্যাসার্ধের খুব ছোটো ছোটো গোলকে ভেঙে ফেলা হলো। যদি ঐ ক্ষুদ্রাতিক্ষুদ্র গোলকগুলির সম্মিলিত পৃষ্ঠতলীয় ক্ষেত্রফল $A$ এবং আয়তন $V$ হয়, তাহলে $A$ আর $V$ -এর অনুপাত কত হবে যখন $R$ প্রায় শূন্যের কাছাকাছি ( $R \to 0$ )?

$A/V \to 0$
$A/V \to 1$
$A/V \to \infty$
$A/V \to R$

[৪]

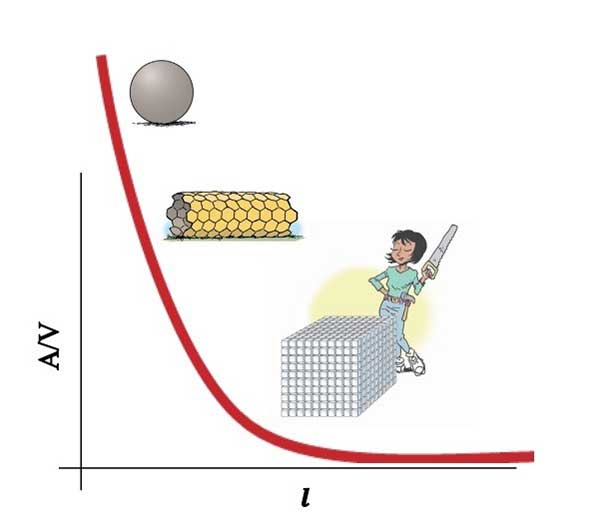
একটা গোলক, ঘনক বা সরু নলের মত বস্তু ধরা যাক। যদি এই আকৃতিগুলোকে একটা দৈর্ঘ্য দিয়েই ব্যাখ্যা করা যায়, ধরা যাক সেই দৈর্ঘ্য-টা $l$ । এটাকে বলে characteristic length scale। গোলকের ক্ষেত্রে এটা হবে ব্যাস, ঘনকের ক্ষেত্রে বাহু আর সরু নলের ক্ষেত্রে দৈর্ঘ্য। যদি $l$ শূন্যের কাছাকাছি যায় ( $l \to 0$ ), তাহলে দেখা যাচ্ছে $A/V$ অসীমের কাছাকাছি যাচ্ছে, অর্থাৎ $A/V \to \infty$ । এই কথাটার মানে কি ?

এর আসলে কোনো মানে নেই। এটা শুধু অঙ্কের ভাষা।
যদি বড় গোলক, ঘনক বা নলটাকে ছোট ছোট ন্যানোগোলক, ন্যানোঘনক কি ন্যানোনল-এ ভাঙ্গা হয়, এদের সম্মিলিত পৃষ্ঠতলের ক্ষেত্রফল অনেক, অনেক গুণ বেড়ে যাবে।
এর মানে কি, আমি জানি না।

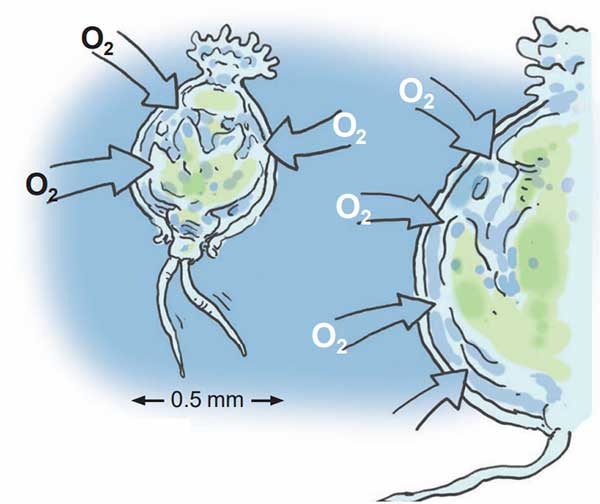
[৫]

এই ছোট্ট জীবটার নাম ‘রোটিফার’ (Rotifer)। এদের শ্বাস নেওয়া মানে সরাসরি চামড়ার মাধ্যমে অক্সিজেন শোষণ করা, তারপর সেটা ব্যাপন প্রক্রিয়ায় (diffusion) দেহের চতুর্দিকে চালান করা। Rotifer-এর বেঁচে থাকার জন্য শোষিত অক্সিজেনের পুরোটাই প্রয়োজন। এখন কোনো যাদুবলে যদি এই Rotifer-টার ব্যাস আগের দ্বিগুণ করে দেওয়া যায়, তাহলে কি সেটা বেঁচে থাকার জন্য প্রয়োজনীয় অক্সিজেন শোষণ করতে পারবে?

হ্যাঁ, কারণ ছোটো এবং বড়, দুটো Rotifer-এরই রাসায়নিক গঠন এক।
হ্যাঁ, কারণ বড় Rotifer-টার পৃষ্ঠতলীয় ক্ষেত্রফল বেশি হওয়ায় শোষিত অক্সিজেনের পরিমাণও বেশি হবে।
না, কারণ বড় Rotifer-টাকে আগের তুলনায় 8 গুণ বেশি অক্সিজেন সরবরাহ করতে হবে; কিন্তু তার পৃষ্ঠতলীয় ক্ষেত্রফল আগের তুলনায় মাত্র 4 গুণ হবে।
না, কারণ বড় Rotifer-এর দেহে অক্সিজেনকে বেশিটা পথ অতিক্রম করতে হবে।

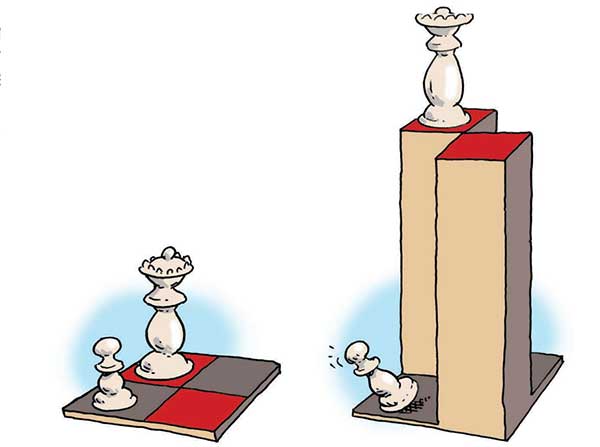
[৬]

এই অতিসাধারণ দাবা বোর্ডে মাত্র চারটে বর্গাকৃতির ঘর রয়েছে। একেকটা ঘরের বাহুর দৈর্ঘ্য 1 cm। যদি দু’টো বর্গাকৃতির ঘরকে ওপরের দিকে টেনে 5 cm লম্বা করে দেওয়া যায়, তাহলে পৃষ্ঠতলীয় ক্ষেত্রফলের কতটা বৃদ্ধি হবে? এক্ষেত্রে বোর্ডটার নিচের দিকটা উপেক্ষা করতে পারো।

50%
100%
400%
1000%

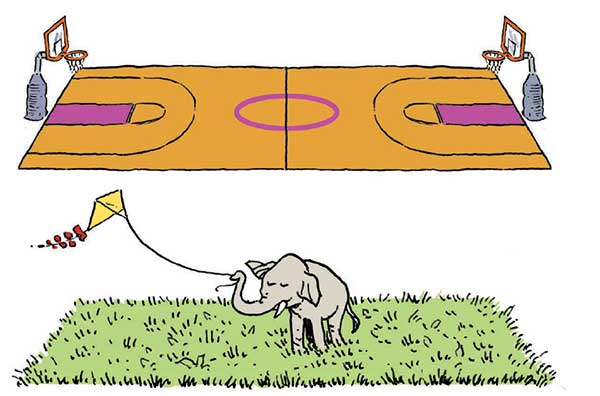
[৭]

কোনটার পৃষ্ঠতলীয় ক্ষেত্রফল বেশি হবে — মসৃণ কাঠের মেঝেওয়ালা একটা বাস্কেটবল কোর্ট নাকি সমান দৈর্ঘ্য-প্রস্থের একটা আয়তাকার (rectangular) ঘাসজমি?

দু’টো উদাহরণের ক্ষেত্রেই পৃষ্ঠতলীয় ক্ষেত্রফল এক।
বাস্কেটবল কোর্ট-টা।
ঘাসযুক্ত মাঠটা।
এই প্রশ্নের উত্তর দেওয়ার মতো যথেষ্ট তথ্য নেই।

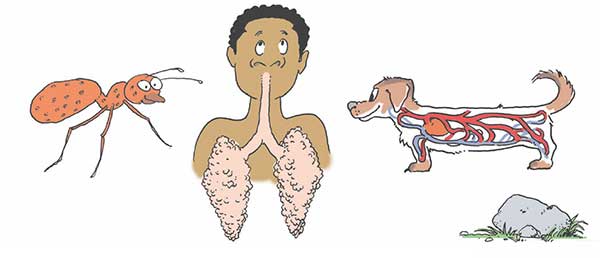
[৮]

কিছু ক্ষুদ্রাতিক্ষুদ্র প্রাণী ব্যাপন প্রক্রিয়ায় (diffusion) চামড়া দিয়ে অক্সিজেন নিয়ে শরীরের ভেতরকার কলাগুলিতে পাঠায়। কিন্তু, আকারে বড় হলে আর এই পদ্ধতি কাজ করে না, তখন অন্য ব্যবস্থা করতে হয়। নিচের কোন অভিযোজনটা একটা বড় প্রাণীকে যথেষ্ট অক্সিজেনের জোগান দিতে সাহায্য করতে পারে?

চামড়ায় অনেকগুলো ছোট ছোট ফুটো। ফুটোগুলি দিয়ে প্রাণীটা অনেকটা জায়গা জুড়ে বাইরে থেকে অক্সিজেন নিতে পারে।
শরীরে রক্তজালিকা (network of blood vessels)। এর মাধ্যমে অক্সিজেন-সমৃদ্ধ রক্ত প্রাণীটার দেহের অতি অভ্যন্তরীণ অংশেও পৌঁছে যেতে পারে।
ফুসফুসের জটিল এবং অসংখ্য বায়ুথলিযুক্ত গঠন। এই থলিগুলির পৃষ্ঠতলীয় ক্ষেত্রফল সবসুদ্ধ অনেকটাই হয়, ফলে অনেকটা জায়গা জুড়ে বায়ুর অক্সিজেন রক্তের সাথে মিশতে পারে।
ওপরের সবগুলিই।
ওপরের কোনোটাই নয়।

[৯]

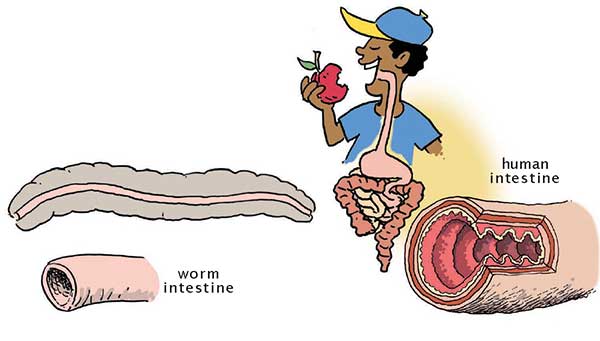
একটা প্রাণী তার অন্ত্রের (intestine) দেয়ালগুলো দিয়ে খাদ্যের পুষ্টি শরীরে গ্রহণ করে। একটা কেঁচোর অন্ত্র হয় সোজা, তার দেওয়াল মসৃণ। কিন্তু বিবর্তনের ফলে মানুষের অন্ত্র বেশ লম্বা এবং পাকানো, দেওয়ালগুলোতেও ভাঁজ রয়েছে। এরকম তফাৎ কেন?

কেঁচো শুধুমাত্র মাটি খায় বলে ওতেই চলে যায়।
মানুষের শরীর অনেকটা বড়। পুরো শরীরের মাপে পুষ্টি জোগান দিতে গেলে অন্ত্রের বেশি পৃষ্ঠতলীয় ক্ষেত্রফল প্রয়োজন। সরল সোজাসাপটা অন্ত্র থেকে যথেষ্ট পৃষ্ঠতলীয় ক্ষেত্রফল পাওয়া যাবে না।
মানুষের পেটে অনেকটা জায়গা রয়েছে, সেই জায়গাটা তো কিছু একটা দিয়ে ভরতে হবে।
কেঁচোর মুখ নেই।

[১০]

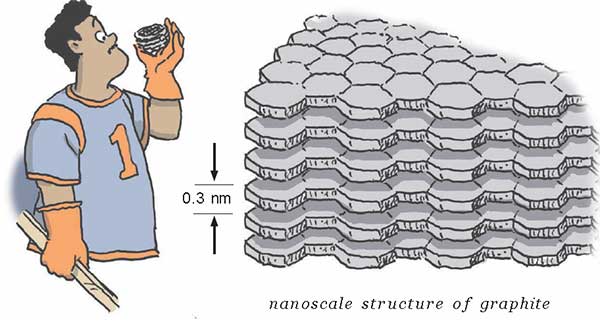
লেস্টার-এর কাছে একটা আইস হকি পাক (puck) আছে। সেটা একটা গ্রাফাইট-এর (graphite) তৈরী ঘনক (cube), তার বাহু 1 cm। গ্রাফাইট আসলে স্তরে স্তরে গ্রাফিন (graphene) বসিয়ে তৈরী, আর গ্রাফিন হলো কার্বন অণুর একটা বিশেষ দ্বিমাত্রিক সজ্জা। একেকটা স্তর 0.3 nm বা 3 X 10^-10 m পুরু। হকি পাক-টার পৃষ্ঠতলীয় ক্ষেত্রফল এখন কত, আর যদি সবকটা স্তরকে আলাদা করা হয়, তাহলে গোটা জিনিসটার উপর আর নিচের পৃষ্ঠতলীয় ক্ষেত্রফল কত হবে? একেকটা স্তরের ধারের দিকটা ধরার দরকার নেই।

স্তরগুলোর ক্ষেত্রফল = 6,667 m², মূল ঘনকটার ক্ষেত্রফল = 10^-4m²,
স্তরগুলোর ক্ষেত্রফল = 6,667 m², মূল ঘনকটার ক্ষেত্রফল = 6 X 10^-4m²,
স্তরগুলোর ক্ষেত্রফল = 3,333 m² , মূল ঘনকটার ক্ষেত্রফল = 6 X 10^-2m²,
স্তরগুলোর ক্ষেত্রফল = 6,66,667 m², মূল ঘনকটার ক্ষেত্রফল = 6 X 10^-4m²,

[১১]

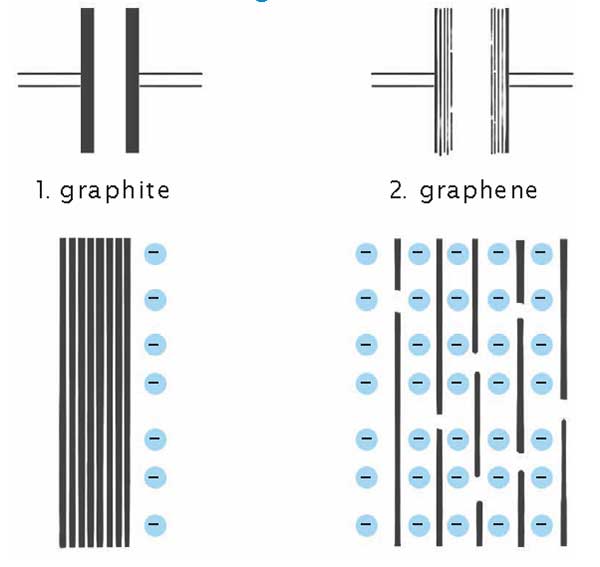
নিচে দুটো ধারক (capacitor) দেখানো হলো। প্রথম ধারকটা গ্রাফাইটের প্লেট দিয়ে তৈরী। দ্বিতীয় ধারকটার প্লেটদুটো পরস্পরের সাথে আলগা ভাবে যুক্ত graphene-এর পাতলা পাতলা স্তর দিয়ে গঠিত। graphene-এর স্তরগুলি ঐ গ্রাফাইটের টুকরো থেকেই পাওয়া গেছে। যদি ধারক দুটোর ভর এবং অন্যান্য চারিত্রিক বৈশিষ্ট্য একই হয়, কোন ধারকটা বেশি আধান (charge) ধরে রাখবে?

দুটো ধারকই একই পরিমাণ আধান ধরে রাখবে।
প্রথম ধারকটা, কারণ এর প্লেট-এর ঘনত্ব (density) বেশি।
দ্বিতীয় ধারকটা, কারণ এর পৃষ্ঠতলীয় ক্ষেত্রফল (surface area) বেশি।
প্রথম ধারকটা, কারণ গ্রাফিনের থেকে গ্রাফাইট বেশি পুরু।

[১২]

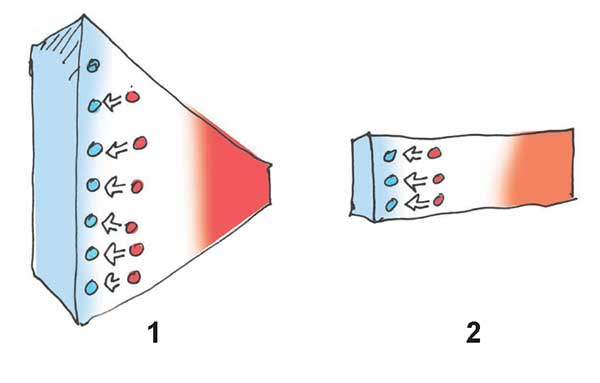
কোনো পদার্থের মধ্যে দিয়ে তাপ প্রবাহিত হয় যখন পদার্থের উচ্চশক্তিসম্পন্ন কণাগুলি নিম্নশক্তিসম্পন্ন কণা ও ফোননের সাথে সংঘর্ষ করে। নিচে দুটো ব্লক-এর ছবি দেওয়া হলো। এগুলোর বাঁদিক-টা ঠান্ডা, ডানদিকটা গরম। প্রথমটার ঠান্ডা দিকটার পৃষ্ঠতলীয় ক্ষেত্রফল অনেকটা বেশি। বাদবাকি সবকিছু, যেমন বস্তুদুটোর ভর, দৈর্ঘ্য, উপাদান, উষ্ণতার পার্থক্য, ইত্যাদি একই। এই দুটোর মধ্যে কোন ব্লক-টাতে গরম অংশ থেকে ঠান্ডা অংশে তাপপ্রবাহের হার বেশি?

প্রথমটাতে, কারণ ওতে সংঘর্ষ ঘটানোর জন্য বেশি পরিমাণে নিম্নশক্তিসম্পন্ন কণা রয়েছে।
দ্বিতীয়টাতে, কারণ ওতে তাপ বেশি ঘনীভূত রয়েছে।
দুটোর ক্ষেত্রে একই হবে কারণ উষ্ণতার পার্থক্য একই।
যা বলা হয়েছে, শুধু তার ভিত্তিতে এই প্রশ্নের উত্তর দেওয়া সম্ভব নয়।

[১৩]

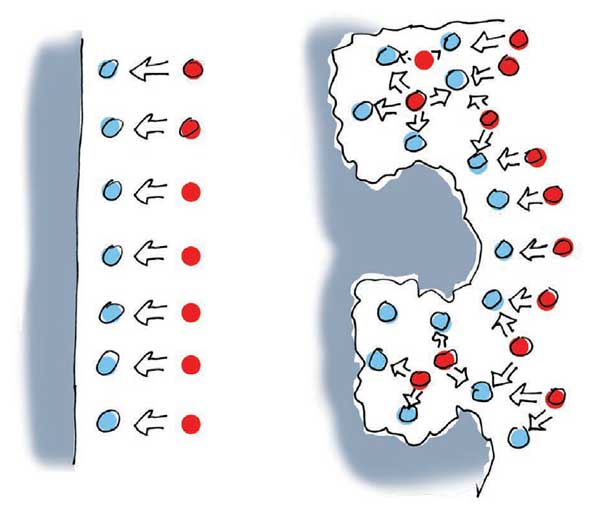
নিচে একই আকৃতির দুটো লোহার ব্লক দেখানো হলো। দুটোরই একদিকের উষ্ণতা 500°C এবং অন্যদিকের 0°C। প্রথম ব্লকের ঠান্ডা দিকটা এক্কেবারে মসৃণ, দ্বিতীয় ব্লকের ঠান্ডা দিকটা ন্যানোমিটার স্তরে দেখলে অমসৃণ। কোন ব্লকের ক্ষেত্রে তুলনামূলকভাবে দ্রুত তাপ প্রবাহিত হবে?

প্রথম ব্লকে তাপপ্রবাহ দ্রুততর হবে, কারণ দ্বিতীয় ব্লকে ন্যানোমিটার স্কেলের এবড়োখেবড়োগুলো তাপপ্রবাহে বাধা দেবে।
প্রথম ব্লকে তাপপ্রবাহ দ্রুততর হবে, কারণ দ্বিতীয় ব্লকটাকে আরো একটা ব্লকের সংস্পর্শে আনলে মাত্র কয়েকটা জায়গাতেই ছোঁয়াছুঁয়ি হওয়া সম্ভব হতো।
দ্বিতীয় ব্লকে দ্রুততর হবে কারণ দ্বিতীয় ব্লকটার ক্ষেত্রে কার্যকরী পৃষ্টতলটা (effective surface) অনেকটা বড়।
দুটো ব্লকের ক্ষেত্রেই একই হবে কারণ উভয়ের ক্ষেত্রেই তাপ নতিক্রম (temperature gradient) একই।

(প্রশ্নগুলো মূল ইংরাজি থেকে বাংলায় অনুবাদ করেছে কাঁথি-র প্রভাতকুমার কলেজ-এর পারমিতা গিরি ও বিদেশ চয়ন সাহু।)

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.