21-12-2024 15:46:23 pm

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

নিউরাল নেটওয়ার্ক-এর অঙ্ক কেমন দেখতে?

অনির্বিৎ

(University of Pennsylvania)

17 Aug 2019

Link: https://bigyan.org.in/mathematics-of-neural-networks

%e0%a6%a8%e0%a6%bf%e0%a6%89%e0%a6%b0%e0%a6%be%e0%a6%b2-%e0%a6%a8%e0%a7%87%e0%a6%9f%e0%a6%93%e0%a7%9f%e0%a6%be%e0%a6%b0%e0%a7%8d%e0%a6%95-%e0%a6%8f%e0%a6%b0-%e0%a6%85%e0%a6%99%e0%a7%8d%e0%a6%95

মেশিন লার্নিং-এর দৌলতে অনেক ক্ষেত্রেই যন্ত্রের সাথে মানুষের তফাৎ করা যায়না। যন্ত্র প্রশিক্ষণের মাধ্যমে বা বিনা প্রশিক্ষণেও অনেক কাজ করে ফেলতে পারে যেখানে এতদিন মানুষের একাধিপত্য ছিল। হাতের লেখা পড়া, ছবি দেখে চিনে ফেলা, দাবার ছক বার করা, এসবই এখন কৃত্রিম বুদ্ধিমত্তা বা আর্টিফিশিয়াল ইন্টেলিজেন্স-এর আওতায় এসে গেছে। আর্টিফিশিয়াল ইন্টেলিজেন্স দীর্ঘকাল ঝিমিয়ে থেকে এখন যে মাথা চাড়া দিয়ে উঠেছে, তার আড়ালে রয়েছে ডিপ নিউরাল নেটওয়ার্ক। কি এই নিউরাল নেটওয়ার্ক? কেমন হয় এর অঙ্ক?

কিংবদন্তি সত্যজিৎ রায়ের কাছে আমাদের বাঙালিদের ঋণের শেষ নেই। শুধু কালজয়ী চলচ্চিত্রেই সেই ঋণের ঝুলি শেষ হয়না। বইয়ে ঠাসা বাঙালি গৃহস্থালীতে বড় হতে হতে আমাদের ‘আর্টিফিশিয়াল ইন্টেলিজেন্স’ বা কৃত্রিম বুদ্ধিমত্তার সাথে পরিচয় ঘটে সত্যজিৎ রায়ের হাত ধরেই। কেন, প্রফেসর শঙ্কু-র গল্পের রোবু বা বিধুশেখর যখন প্রায় মানুষের মতো আচরণ করে, সেটাও একরকম কৃত্রিম বুদ্ধিমত্তা বৈকি!

একদিক দিয়ে দেখলে, প্রফেসর শঙ্কুর মিষ্টি রোবোটগুলোর সাথে আমাদের প্রথম আলাপ হয়ে ভালোই হয়েছে। নইলে আইজ্যাক অ্যাসিমভ-এর রোবোটিক্স-এর তিন তত্ত্বের সামনে পড়লে রোবটের দুনিয়াদখলের সম্ভাবনায় ভীত হয়ে থাকতে হতো [১]। তবে, এই ২০১৯-এও মিষ্টি-স্বৈরাচারী কোনো রোবট-ই কল্পনার জগৎ থেকে বাস্তবে আসেনি। কিন্তু গত পাঁচ-ছ বছরে এক নাটকীয় পরিবর্তন হয়েছে। সেই পরিবর্তনের কথাই আমরা এই লেখায় বোঝার চেষ্টা করবো।

প্রথমেই একটা স্বীকারোক্তি। হালে কৃত্রিম বুদ্ধিমত্তার জগতে যে বিপ্লবের সূচনা হয়েছে, সেই নিয়ে বিশেষজ্ঞদের মধ্যে নানারকমের মত রয়েছে। সবাই একইরকম আশাবাদী নয়। এবং আমি যা বলতে চলেছি, সেটাও একেবারে নিরপেক্ষ হবেনা। তাতে আমার নিজের গবেষণার কিছুটা ছায়া হয়তো পড়বে।

নিউরাল নেটওয়ার্ক-এর প্রভাব সর্বত্র

পাঠকের অনেকেই হয়তো শুনেছেন, সম্প্রতি AlphaZero-র মতো তথাকথিত যন্ত্র দাবার মতো খেলায় সবরকম রেকর্ড ছাপিয়ে গেছে। এমন সব ছকের সন্ধান পাওয়া গেছে যা দাবার ইতিহাসে আজ অব্দি কেউ দেখেনি। কিন্তু আক্ষেপের বিষয়, এই ধরণের কৃত্রিম বুদ্ধিমত্তা একেবারেই প্রফেসর শঙ্কুর রোবটের মতো নয়। একসাথে বিভিন্ন রকমের মেধা এরা দেখতে পারেনা।

তবে মানুষের বুদ্ধিমত্তাকে কোনো একটা সংকীর্ণ গণ্ডির মধ্যে বিচার করলে যন্ত্রের সাথে তফাৎ করা দায় হয়ে ওঠে। দাবা কিংবা পোকার-এর মতো খেলায় হাজার হিসেবনিকেশ করে চাল দিতে হবে? যন্ত্রও পারে। ভ্যান গো-র স্টাইল অনুকরণ করে ছবি আঁকতে হবে? এটাও যন্ত্র পারে। পটাপট একটা ভাষা থেকে আরেকটাতে অনুবাদ করতে হবে? এখানেও যন্ত্র জাঁকিয়ে বসেছে। গত কয়েক বছরে সবই অটোমেশন-এর আওতায় চলে এসেছে। যাকে বলে ‘ডিপ নিউরাল নেটওয়ার্ক’ বা ‘DNN’ বা ‘নিউরাল নেটওয়ার্ক’ বা ‘নিউরাল নেটস’ বা মাঝেমাঝে শুধুই ‘নেটস’ (nets), এর গণনাশক্তিকে হাতের মুঠোয় এনে তবেই এই চমৎকার সম্ভব হয়েছে। যেভাবে একটা নিউরাল নেটওয়ার্ক-কে “ট্রেন” করে একদম মানুষের মতো কাজ করানো যায়, তাকেই বলে “ডিপ লার্নিং” (deep learning)।

নিউরাল নেটওয়ার্ক নিয়ে নিজে ঘাঁটাঘাঁটি করতে চাইলে

নিউরাল নেটওয়ার্ক-এর এইসব চোখধাঁধানো কেরামতি দেখতে TensorFlow কিংবা PyTorch-এর মতো সফটওয়্যার বিনামূল্যে নিজের কম্পিউটার-এই বসানো যায়। এইসব সফটওয়্যার-এর স্রষ্টারা ক্রমশ চেষ্টা করছেন যাতে আরো বেশী লোকে চটপট হাত পাকিয়ে এইসব প্রযুক্তিকে কাজে লাগাতে পারেন। এর ফলে Google Colab-এর মতো প্ল্যাটফর্ম তৈরী হয়েছে যেখানে সরাসরি কোড লিখে ছোটোখাটো নিউরাল নেটওয়ার্ক চালানো যায়। একটা গোটা জবরজং সফটওয়্যার নিজের কম্পিউটার-এ বসাতে হয়না।

আপাতত ডিপ লার্নিং নিয়ে উৎসাহ আনতে চাইলে এই ওয়েবসাইট-টাতে ঘুরে আসতে পারেন: https://thispersondoesnotexist.com/। পাতাটা যতবার রিফ্রেশ করা হবে, একটা আপাত মানুষের ছবি দেখতে পাবেন, হয়তো মাঝেমধ্যে একটু খুঁত সমেত। কিন্তু বললে বিশ্বাস করবেন না, কৃত্রিমভাবে নিউরাল নেটওয়ার্ক-এর মাধ্যমে প্রত্যেকটা ছবির জন্ম হয়েছে! অন্যভাবে বললে, এই মানুষগুলো সম্পূর্ণরূপে ওই নেটওয়ার্ক-এর কল্পনার রাজ্যের বাসিন্দা, বাস্তবে এদের কোনো অস্তিত্বই নেই!

নিউরাল নেট-এর ম্যাজিক-এর আড়ালে কি হচ্ছে

কিভাবে একটা নেটওয়ার্ক এরকম জলজ্যান্ত মানুষের ছবি এঁকে ফেললো? কিভাবে, সেটা আমরা খুব ভালো বুঝিনা। যতটা অংশ বোধগম্য, তার নাগাল পেতেই গণিতের একটা উচ্চতর শাখার আশ্রয় নিতে হয়, তার নাম ‘অপটিমাল ট্রান্সপোর্ট’ (optimal transport)। এই শাখাতেই গবেষণা করে ২০১০-এ সেড্রিক ভিলানি ফিল্ডস মেডেল পেয়েছিলেন (অঙ্কের জগতে নোবেল-এর সামিল)। নিউরাল নেটওয়ার্ক-এর জগৎটাকে এই অজানা-অচেনা গণিতের প্রয়োগশালা হিসেবে ভাবা যেতে পারে। কিন্তু আমরা সবে এই গণিতে বুড়িছোঁয়া ছুঁয়েছি মাত্র।

আশা করছি কোনো একদিন এই জটিল শাখাটির ওপরও আলোকপাত করতে পারবো। কিন্তু এই লেখায় শুধু নিউরাল নেটওয়ার্ক-এর একদম গোড়ার গাণিতিক কাঠামোটা নিয়েই আলোচনা করবো।

কাজ যে করছে সেটা বুঝবো কিকরে

নিউরাল নেটওয়ার্ক-এর যে উন্নতিগুলোর কথা আগে বললাম, সেগুলো প্রয়োগের দিক থেকে একদম তাজা তাজা কালকের গবেষণা। কিন্তু নিউরাল নেটওয়ার্ক-এর কোনো তত্ত্ব যাচাই করতে এগুলো ব্যবহার করা হয়না। কোনো তত্ত্বের সাফল্য মাপতে আমরা কয়েক দশক পুরোনো কিছু স্ট্যান্ডার্ড পরীক্ষা করে থাকি। বাজারে কোনো নতুন তত্ত্ব এলেও এই পরীক্ষার মধ্যে দিয়ে যায়।

এক ধরণের পরীক্ষাতে একগোছা ছবি নিয়ে কোনো একটা অর্থবহ বিভাগে ভাগ করা হয়। এখানে ছবি বলতে ভিতরে ভিতরে একটা বহুমাত্রিক ভেক্টরের কথা বলা হচ্ছে (ছবির কোথায় কি রং, সেটা সংখ্যায় প্রকাশ করলে, যে সংখ্যার ম্যাট্রিক্স পাওয়া যায়, তার কথাই বলা হচ্ছে এখানে)। নিউরাল নেটওয়ার্ক (বা যে যন্ত্রকে নিউরাল নেটওয়ার্ক হিসেবে ভাবা হচ্ছে) সেইসব ভেক্টরে সমৃদ্ধ হয়ে ছবিগুলোর একটা বিভাগ স্থির করবে। এরপর নতুন কোনো ছবি এলে কোন ভাগে পড়বে সেটাও বলে দেবে এই নেটওয়ার্ক।

তুলনা করুন একটা ন’মাসের শিশুর সাথে যে অবলীলায় কোনো রোজকার সামগ্রীকে তার ছবির সাথে মেলাতে পারে। এই ন’মাসের শিশুর কাছে নিউরাল নেটওয়ার্ক হেরে ভূত! শিশু একটিবার একখান ফল দেখেই পরের বার ফলটা চিনতে প্রস্তুত হয়ে যেতে পারে। কিন্তু একটা নিউরাল নেটওয়ার্ক-কে অনেক অনেক ছবি দেখিয়ে তবেই সেই পর্যায়ের প্রস্তুতি দেওয়া যায়। কেন এই আকাশপাতাল তফাৎ? সেটাও রহস্য, গবেষণা সবেমাত্র চালু হয়েছে এবিষয়ে।

দুটো ছবির ভান্ডার বিশেষ করে এই পরীক্ষার কাজে ব্যবহৃত হয়ে থাকে। এরা হলো:

[১] CIFAR ডেটাবেস। CIFAR-এর পুরো কথাটা Canadian Institute For Advanced Research [২]।

[২] MNIST ডেটাবেস। MNIST-এর পুরো কথাটা Modified National Institute of Standards and Technology [৩]।

প্রথমটাতে অর্থাৎ CIFAR ডেটাবেস-এ লক্ষ লক্ষ অল্প রিসোলিউশন-এর ছবি রয়েছে, হাজার হাজার ভাগে বিভক্ত। যেমন, পাখি, এরোপ্লেন, গাড়ি, ইত্যাদি। এই ছবির ভান্ডার থেকে যে কোনো একটা ছবি দেওয়া হলে তাকে সঠিক ভাগে ফেলতে হবে। সেটাই নিউরাল নেটওয়ার্ক-এর সাফল্যের মাপকাঠি। নিচের ছবিতে MNIST সংগ্রহের একটা অংশ দেওয়া হলো। এটা আর কিছুই না, ০ থেকে ৯ অব্দি হাতে লেখা সংখ্যার সংগ্রহ। নিউরাল নেটওয়ার্ক-কে একবার প্রস্তুত করা হলে ওই সংগ্রহের মধ্যে থেকে যে কোনো একটা সংখ্যা দিলে তাকে চিনতে পারার কথা। আজও আমরা এই MNIST-কেই নিউরাল নেটওয়ার্ক-এর ন্যূনতম পরীক্ষা হিসেবে ব্যবহার করে থাকি। আর কিছু পরীক্ষা পারুক না পারুক, এই পরীক্ষায় উত্তীর্ণ হতে হবে। এখানে বলে রাখি, MNIST-এর বাংলা সংস্করণ-ও পাওয়া যায় কিন্তু!

একটা লক্ষ্যণীয় বিষয় হলো, CIFAR-ভিত্তিক পরীক্ষাটা অর্থাৎ ছবির বিভাগ নির্ণয় কিন্তু MNIST-ভিত্তিক পরীক্ষা অর্থাৎ হাতে লেখা সংখ্যা চেনার থেকে অনেক বেশি শক্ত। কিন্তু অঙ্কের দিক থেকে কেন একটা আরেকটার থেকে বেশি শক্ত হবে, সেটা এখনো অজানা। একটা নিউরাল নেটওয়ার্ক-এর কাছে কখন যে কাজটা সরল আর কখন শক্ত, এই সারল্যের তারতম্যটাও গবেষকদের কাছে রহস্য। এবিষয়ে সবেমাত্র গবেষণা চালু হয়েছে। একটা আশাব্যঞ্জক গবেষণার দিশা হলো, “t-SNE” (“t-distributed Stochastic Neighbor Embedding”) বলে একটা পদ্ধতির গাণিতিক সুতোর জট ছাড়ানোর। তবে এই নিয়ে আর কথা বাড়াচ্ছি না। উৎসাহী পাঠক এবিষয়ে আরো ঘেঁটে দেখতে পারেন।

আপাতত নিউরাল নেটওয়ার্ক-এর প্রয়োগ আর পরীক্ষা পেরিয়ে সবচেয়ে জনপ্রিয় নিউরাল নেটওয়ার্ক-এর আরো গভীরে যাওয়া যাক: ডিপ নিউরাল নেটওয়ার্ক বা DNN।

নিউরাল নেটওয়ার্ক-এর খুব সংক্ষিপ্ত একটা ইতিহাস

সেই ১৯৫৮-এ কর্নেল বিশ্ববিদ্যালয়ের এক মনস্তত্ত্ববিদ ফ্র্যাঙ্ক রোজেনব্ল্যাট একটা গবেষণাপত্রে DNN-এর ধারণাটা দিয়েছিলেন, তবে থেকে ধারণাটা কোনো না কোনো আকারে টিকে গেছে। উনি নাম দিয়েছিলেন ‘পারসেপট্রন’ (perceptron)। তবে অনেকে বলবেন, নিউরাল নেটওয়ার্ক সম্বন্ধে আধুনিক চিন্তাধারা এসেছে ১৯৮৬-এর একটা গবেষণাপত্র থেকে, নাম তার “Learning representations by back-propagating errors” [৪]। এর লেখকদের মধ্যে Geoffrey Hinton-কে ডিপ লার্নিং-এর পথিকৃৎ হিসেবে ভাবা হয় এবং মজার বিষয় হলো, এনার আন্ডারগ্রাজুয়েট পড়াশোনাও মনস্তত্ত্ববিদ্যা নিয়ে!

কিন্তু নিউরাল নেটওয়ার্ক-এর ধারণা থাকলে কি হবে, বাস্তবে যা করা যেত, তা খুবই সীমিত। এই সময়টাকে বলা হতো AI winter বা কৃত্রিম বুদ্ধিমত্তার শীতাবস্থা। এই দীর্ঘ শীতে পরিত্রাতা হয়ে এলো কম্পিউটার হার্ডওয়্যার। হঠাৎই অনেক অভাবনীয় গণনা হার্ডওয়্যার-এর অসম্ভব উন্নতির সৌজন্যে হাতের নাগালের মধ্যে চলে এলো। ২০১২-র একটি গবেষণাপত্র, যার নাম “ImageNet Classification with Deep Convolutional Neural Networks”, তাতে লেখকরা দেখালেন যে একটা ডিপ নিউরাল নেটওয়ার্ক-এর পক্ষে ছবি চেনা ও তার অর্থবহ বিভাজন সম্ভব [৫]। প্রায় মানুষের মতোই নিখুঁতভাবে! অনেকে বলেন এই গবেষণাপত্রটিই আজকের কৃত্রিম বুদ্ধিমত্তার বিপ্লবের সূচনা করেছিল।

নিউরাল নেটওয়ার্ক কেমন দেখতে

এবার বোঝার চেষ্টা করা যাক, গাণিতিকভাবে একটা নিউরাল নেটওয়ার্ক কেমন দেখতে হয়। DNN-কে এক অর্থে গাণিতিক সার্কিট বলা যায়। এরা আদতে এক ধরণের ফাঙ্কশন (function) বা অপেক্ষক যাদের তড়িত্প্রবাহী সার্কিটের মতো সার্কিট দিয়ে আঁকা যায়। খালি এই সার্কিটগুলো তড়িতের পরিবর্তে অঙ্ক কষার নির্দেশ বহন করে। সার্কিটে যে সংখ্যাগুলো প্রবেশ করলো (input), তাদের উপর গুণ বা যোগ প্রক্রিয়া সম্পন্ন করার নির্দেশ। নিচের ছবিতে যেমন $X_1, X_2, X_3$ তিনটে সংখ্যা প্রবেশ করে বাহুগুলো দিয়ে গেলে $W_1X_1 + W_2X_2 + W_3X_3$ সংখ্যাটা দেয়।

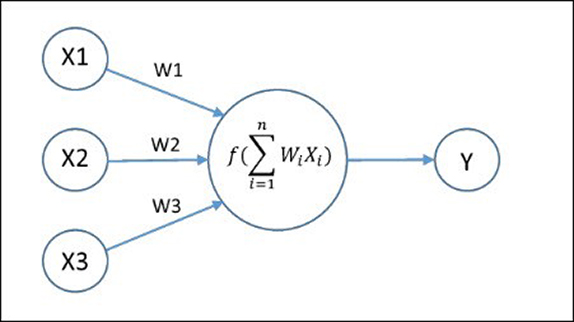
একটা তড়িৎপ্রবাহী সার্কিটকে দিয়ে কাজের কাজ করাতে গেলে তাতে আরো জটিলতা আনতে হয়: রেজিস্টর, ইন্ডাক্টর কিম্বা ক্যাপাসিটর বসাতে হয়। সেইরকমই, এইসব গাণিতিক সার্কিটেও যোগ-গুণ প্রক্রিয়ার পর সংখ্যাগুলো একপ্রকার গেট-এর মধ্যে দিয়ে যায়। গেট-টা সাধারণত একটা নন-লিনিয়ার অপেক্ষক হয় [৬]। উপরের ছবিতে একে $f(W_1X_1 + W_2X_2 + W_3X_3)$ বা $f(\displaystyle\sum_{i=1}^{n}W_iX_i)$ চিহ্নের সাহায্যে দেখানো হয়েছে। এই ছবিটা নিউরাল নেটওয়ার্ক-এর একটা সরলতম উদাহরণ।

এই বিষয়ে যারা চর্চা করেন, তাদের কাছে এই :

$f : {\Bbb R} \rightarrow {\Bbb R}$

(অর্থাৎ একটা বাস্তব সংখ্যা দিলে আরেকটা আসে), এইটাকে বলে অ্যাকটিভেশন ফাঙ্কশন (activation function)। যেটা ইনপুট হিসেবে একটা ত্রিমাত্রিক ভেক্টর-এর লিনিয়ার কম্বিনেশন (অর্থাৎ তিনটে বাস্তব সংখ্যা-এর লিনিয়ার কম্বিনেশন) নেয় এবং আউটপুট হিসেবে $f(W_1X_1 + W_2X_2 + W_3X_3)$ দেয়। যে তিনটে বাস্তব সংখ্যা $W_1, W_2, W_3$ দিয়ে ইনপুট সংখ্যাগুলোকে গুণ করা হলো, তাদের বলে ওজন বা ওয়েইট (weight)। এখানে গেট থেকে একটাই বহির্মুখ বাহু রয়েছে। সাধারণত অনেকগুলো থাকে এবং তার অর্থ হলো, সবকটা বাহুতেই একই সংখ্যা পাচার হচ্ছে, গন্তব্যস্থল আলাদা।

একটা সহজ উদাহরণ

এখন একাধারে সবাই মেনে নিয়েছেন যে অ্যাকটিভেশন ফাঙ্কশন হিসেবে ReLU বা Rectified Linear Unit অপেক্ষকটির তুলনা হয়না। অপেক্ষকটি এইরকম:

${\text{ReLU} : {\Bbb R} \rightarrow {\Bbb R}}\\{x \hspace{2mm} \rightarrow \hspace{2mm} \max(0,x) }$

অর্থাৎ, একটা সংখ্যা ধনাত্মক হলে সংখ্যাটাই পাওয়া যাবে আর ঋণাত্মক হলে শূন্য পাওয়া যাবে।

নিউরাল নেটওয়ার্ক-এর সার্কিট-এ কি কি থাকে, সেগুলো দেখলাম। এবার দেখা যাক এই টুকরোগুলো জুড়ে একটা নিউরাল নেটওয়ার্ক কিভাবে বানানো যায়। নেটওয়ার্ক-টার শেষে খুব পরিচিত একটা অপেক্ষককেই পাবো। উদ্দেশ্য এইটা দেখানো, কিভাবে সেই পরিচিত অপেক্ষকটা নিউরাল নেটওয়ার্ক-এর জালের মধ্যে থেকে বেরিয়ে আসে।

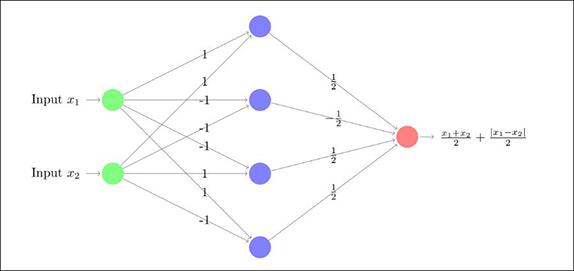
উপরে যে ছবিটা দেখছি, সেটা একটা 1-DNN-এর উদাহরণ। শুরুর ইনপুট আর শেষের আউটপুট-এর মাঝে একটাই স্তর, তাই 1-DNN। এই নিউরাল নেটওয়ার্ক-টার “সাইজ” হলো চার, যেহেতু মাঝে চারটে গেট আছে। প্রত্যেকটা বাহুতে ওজনটাও ছবিতেই দেওয়া আছে। প্রত্যেকটা গেট-এই অ্যাকটিভেশন ফাঙ্কশন উপরে বর্ণিত $\text{ReLU}$ অপেক্ষক। দাবি হলো এই যে নেটওয়ার্ক-এর মধ্যে দিয়ে গেলে ইনপুট সংখ্যা দুটোর মধ্যে বৃহত্তর সংখ্যাটা বেরিয়ে আসে। অর্থাৎ, $\max(x_1, x_2)$ ।

বিশ্বাস হচ্ছে না? অঙ্কটা কষে দেখুন। প্রথমে লক্ষ্য করুন, মাঝের স্তরে সবথেকে উপরের গেট-টাতে বাহুর ওজনগুলো ধরলে যে সংখ্যাটা যাচ্ছে, সেটা $x_1 + x_2$ । আর ওই গেট-টা থেকে গন্তব্যে যে সংখ্যাটা যাচ্ছে, সেটা (আবার বাহুর ওজন ধরলে) $\frac {1}{2} \max\{0, x_1 + x_2\}$ । গন্তব্যে সবকটা বাহু থেকে আসা সংখ্যা যোগ হয়। তাতেই সুরসুর করে বেরিয়ে আসে যে নেটওয়ার্ক-টা তার দুটো ইনপুটের বৃহত্তর সংখ্যাটা ফেরত দিচ্ছে।

দুটো বিশেষ সংখ্যা নিয়ে দেখতে পারেন। ধরুন, $x_1 = 2$ আর $x_2 = 5$ । তাহলে নীল গেটগুলোতে উপর থেকে নিচে দেখলে প্রবেশ করছে $7, -7, 3$ আর $-3$ । গেটগুলো লাল গন্তব্যস্থলে পাঠাচ্ছে এই চারটে সংখ্যা: $\frac {7}{2}$ , $- \frac {1}{2} \max\{0, -7\} = 0$ , $\frac {1}{2}\max\{0, 3\} = \frac {3}{2}$ আর $\frac {1}{2} \max\{0, -3\} = 0$ । এদের যোগফল $5$ , যেটা সত্যিই দুটো ইনপুট-এর মধ্যে বৃহত্তর সংখ্যাটা।

আরেকটু জটিল নেটওয়ার্ক

এটা ছিল একটা স্তর সমৃদ্ধ নিউরাল নেটওয়ার্ক। এতে দুটো সংখ্যার বৃহত্তরটাকে পাওয়া গেল। এই বিষয়ে আরো দখল আনতে চাইলে চারটে সংখ্যার মধ্যে বৃহত্তম সংখ্যাটাকে খুঁজতে দুটো স্তর-ওয়ালা কিম্বা পাঁচটা সংখ্যার মধ্যে খুঁজতে তিনটে স্তর-ওয়ালা নিউরাল নেট বানানোর চেষ্টা করে দেখতে পারেন। আরেক ধাপ এগিয়ে দেখানোর চেষ্টা করতে পারেন যে $n$ -খানা সংখ্যার বৃহত্তরটাকে গণনা করতে চাইলে নিউরাল নেট-এ $\log (n)$ -খানা স্তর থাকলেই যথেষ্ট।

আমরা যারা নিউরাল নেটওয়ার্ক-এর তত্ত্ব বা থিওরি নিয়ে মাথা ঘামাই, তাদের কাছে আরেকটি অপেক্ষক খুব গুরুত্বপূর্ণ:

$f(x) = \max\{0, \frac {1}{\omega} - \frac {1}{\omega^2}|x-a|\}, \omega > 0 , a > 0$

সহজেই দেখতে পারেন, এর মান শুধু $[a - \omega , a + \omega]$ -এর মধ্যে ছাড়া সর্বত্র শূন্য। ওই পরিসরটুকুর মধ্যে অপেক্ষকটার মান একটা ত্রিভুজের মতো আকার ধারণ করে। ত্রিভুজের ডগাটা $x$ -এর মান $a$ হলে আসে। এই অপেক্ষকটাকে একটা স্তর-সমৃদ্ধ নিউরাল নেটওয়ার্ক দিয়েও লেখা যায়। চেষ্টা করো দেখুন। আরেকটু চাপ নিতে চাইলে একাধিক ত্রিভুজ আকারের অপেক্ষক-কেও নিউরাল নেট দিয়ে লিখতে পারেন। (খেয়াল করুন, এখানে ইনপুট হিসেবে কিন্তু একটাই সংখ্যা যাচ্ছে। একের বেশি সংখ্যা ইনপুট হলে এই ত্রিভুজাকার অপেক্ষকের সমতুল্য অপেক্ষকটা কেমন দেখতে হবে, সেটা একেবারেই স্পষ্ট নয়!)

এই যে দু’ধরণের অপেক্ষকের কথা বললাম, ইনপুট সংখ্যাগুলোর বৃহত্তরটা আর একটা ইনপুট সংখ্যার ওপর ত্রিভুজাকার অপেক্ষক, এদের সাহায্যেই আরো এমন জটিল অপেক্ষক তৈরী হয় যাদের নিউরাল নেটওয়ার্ক দিয়ে গণনা করা যায়। কিন্তু কটা স্তর লাগবে সেই নিউরাল নেট-এ, সেটা বার করা মোটেই সোজা নয়। পাঁচটা সংখ্যার বৃহত্তমটাকে বার করতে তিনটে স্তর লাগবেই না দুটোতেও চলবে, আমরা এখনো সেটা জানি না। এই ধরণের প্রশ্নের উত্তর দিতে কিছু ক্ষেত্রে খুব জটিল অঙ্ক ব্যবহার করতে হয়, কিছু ক্ষেত্রে তো এখনো গবেষণা চলছে।

নিউরাল নেটওয়ার্ক সমাধান করা

আরো একধাপ এগোলে, ছবি (diagram) বা “আর্কিটেকচার”-এর (architecture) শরণাপন্ন হতে হয়। নিচে সেইরকম একটা ছবি রইলো। (যারা গ্রাফ থিওরি জানো, তারা ছবিটাকে একটা ডিরেক্টেড অ্যাসাইক্লিক গ্রাফ হিসেবে ভাবতে পারো যেখানে সব বাহুগুলো ডানদিকে নির্দেশ করছে।)

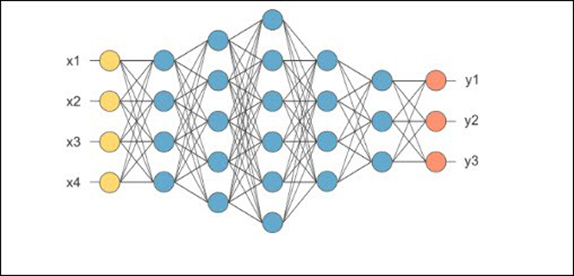
আগের সার্কিটের মতো এখানে বাহুগুলোতে কোনো ওজন দেওয়া নেই। তাহলে, এক অর্থে ছবিটা যত $\Bbb R^4 \rightarrow \Bbb R^3$ অপেক্ষককে গণনা করা যায় এই নেট-এর মাধ্যমে, একাধারে সব্বাইকে বোঝাচ্ছে। খালি অ্যাকটিভেশন ফাঙ্কশনটাকে স্থির রাখা হয়েছে ওই নীল রঙের নোড-গুলোতে, কিন্তু বাহুগুলোর ওপর ওজন যা ইচ্ছে হতে পারে। হলুদ নোড-গুলোতে চতুর্মাত্রিক ইনপুটগুলো আসবে আর কমলা নোড দিয়ে ত্রিমাত্রিক আউটপুট বেরোবে। প্রত্যেকটা বাহুর ওপরও ওজন হিসেবে একটার জায়গায় দুটো বাস্তব সংখ্যা ব্যবহার করা যায়। তারা যদি $a$ আর $b$ হয়, তাহলে এইভাবে বলা যায় যে বাহুতে $x$ ইনপুট এলে $(ax + b)$ আউটপুট পাওয়া যাবে।

অতএব এই নিউরাল নেট দিয়ে কোনো একটা অপেক্ষককে বোঝাতে হলে, যতগুলো বাহু আছে, তার দ্বিগুন ওজনকে নির্ণয় করতে হবে। আজকের দিনে কিছু বিশালকায় নেট-এ (যাদের “AmoebaNet-D” বলে), ছ’হাজার লক্ষ মতো এরম প্যারামিটার নির্ণয় করা যায়। তবে সেটা যে খুব বড়ো একটা সংখ্যা, এরকম ভেবে বসবেন না। মানবমস্তিষ্কে ছ’হাজার কোটি নিউরন রয়েছে এবং একেকটার দশ হাজার মতো সাইন্যাপ্টিক যোগাযোগ আছে অন্যান্য নিউরনের সাথে। আমরা সবচেয়ে শক্তিশালী যে নিউরাল নেটওয়ার্ক-এর মাধ্যমে মস্তিষ্কের অনুকরণ করার চেষ্টা করছি, আসল মস্তিষ্কের দক্ষযজ্ঞের সামনে তাকে প্রায় শিশু বলা চলে!

এবার মোটামুটি নিউরাল নেটওয়ার্ক-এর নকশাটা কিছুটা স্পষ্ট হলো। (একটা গূঢ় প্রশ্ন হলো: যেসব অপেক্ষককে এইরকম নিউরাল নেট-এর মাধ্যমে লেখা যায়, তাদের মধ্যে কতগুলো দ্রুত ওঠানামা করছে। অর্থাৎ, ওই ত্রিভুজাকার অপেক্ষকের মতোই, কিন্তু অনেক, অনেক ত্রিভুজ।)

পরের পরিচ্ছদের প্রিভিউ

এটা যাকে বলে হিমশৈলের মাথাটুকু। এরপর কি রয়েছে, তার একটা আভাস দেওয়া যাক। ডিপ লার্নিং এ যে কোন একটি সমস্যায় (ধরা যাক মেশিনকে দাবা খেলাতে ট্রেন করার প্রক্রিয়ায়) “লস ফাংশান” খুব গুরুত্বপূর্ণ অংশ। ডিপ লার্নিং-এর সমস্যাটি সমাধান করা আখেরে কিছু বাস্তব অপেক্ষককে ক্রমাগত ক্ষুদ্রাতিক্ষুদ্র করায় গিয়ে ঠেকে। এই বাস্তব অপেক্ষকটিই এখানে “লস ফাংশান”। বিভিন্ন অভিজ্ঞতা থেকে বোঝা গেছে যে সমস্যা সমাধানের ব্যাপারে যথেষ্ট দক্ষতা থাকলে লস ফাংশান সরাসরি লিখে ফেলা সম্ভব। এই লস ফাংশান যে কোন কৃত্রিম বুদ্ধিমত্তার সমস্যাকে একটি অপেক্ষক হিসেবে কল্পনা করে, যে অপেক্ষকটি নিউরাল নেটস এর আউটপুটকে ধনাত্মক সংখ্যাতে রূপদানের চেষ্টা করে। আমাদের কাজ হল নিউরাল নেট-এর ওজন এবং অসংখ্য প্যারামিটার-কে বাড়িয়ে কমিয়ে এই লস ফাংশানকে ক্রমশ ছোট করে নিয়ে অভীষ্ট আসল লক্ষ্যে পৌঁছনো। অর্থাৎ এক্ষেত্রে অনেক অনেক নিউরাল নেট গঠন পদ্ধতির বা architecture-এর মধ্যে যথাযথ গঠনটিকে বেছে নেওয়া ভীষণ ভাবে গুরুত্বপূর্ণ। শুধু বেছে নেওয়াই নয়, কোন নিউরাল নেট গঠনের জন্য কোন লস ফাংশান জরুরি তা নির্ধারণ করাও সমান ভাবে গবেষণার দাবি রাখে। বর্তমানে এটি শিল্পের পর্যায় পৌঁছেছে এবং এ বিষয়ে গবেষণা সবেমাত্র শুরু হয়েছে।

মজার ব্যাপার হল, নিউরাল নেট গঠনের সময়ে প্রকৃত লস ফাংশান নিয়ে সম্পূর্ণ ধারণা থাকেনা। এই ধরণের সমস্যা সাধারণত খুব জটিল হয়। কি খোঁজা হচ্ছে, সেই সবন্ধে একটা আধাখ্যাঁচড়া ধারণা নিয়ে শুরু করে তামাম অপেক্ষকদের মধ্যে প্রকৃত অপেক্ষকটাকে খুঁজে বার করতে হবে। এখান থেকেই এক নতুন গবেষণা শাখার জন্ম, যাকে বলা হয় “ স্টকাসটিক অপ্টিমাইজেশান” (stochastic optimization)। অন্য এক দিন নিউরাল নেট এ এই বিষয়টার প্রয়োগ নিয়ে বিস্তারিত আলোচনা করা যাবে। প্রত্যেকদিন বিভিন্ন গবেষণাপত্র নতুন করে এই বিষয়টার ওপর আলোকপাত করছে!

(প্রচ্ছদের ছবি: সূর্যকান্ত শাসমল)

(লেখাটি মূল ইংরেজি থেকে অনুবাদ করেছে ‘বিজ্ঞান’ টীম-এর অনির্বাণ গঙ্গোপাধ্যায় ও শৌর্য সেনগুপ্ত।)

উৎসাহী পাঠকদের জন্য

[১] আইজ্যাক অ্যাসিমভ-এর রোবোটিক্স-এর তিনটে তত্ত্ব বা আইন হলো:

এক, একটা রোবট যেচে বা স্রেফ অনীহায় মানুষের ক্ষতি করতে পারবে না।

দুই, একটা রোবট মানুষের বাধ্য হয়ে থাকবে, যদি না তাতে প্রথম তত্ত্বের সাথে ঠোকাঠুকি লাগে।

তিন, একটা রোবট নিজের অস্তিত্ব রক্ষার সম্পূর্ণ চেষ্টা করবে যদি না তাতে প্রথম বা দ্বিতীয় তত্ত্বের লঙ্ঘন হয়।

এরকম তিনটে তত্ত্ব শুনলে ভয় পাওয়া স্বাভাবিক। মনে হতেই পারে, গল্পে দেওয়া এই তিনটে তত্ত্ব বাস্তবে রোবট মানবে কেন!

[২] CIFAR ডেটাবেস-টা ২০০৯-এ তৈরী করেছিলেন Alex Krizhevsky, Vinod Nair এবং Geoffrey Hinton।

[৩] MNIST ডেটাবেস-টা ১৯৯৮-এর একটা যুগান্তকারী গবেষণপত্রে পেশ করেছিলেন এই বিষয়ের কিছু বাঘা বাঘা গবেষক: Y. LeCun, L. Bottou, Y. Bengio এবং P. Haffner। গবেষণাপত্রটির নাম “Gradient-Based Learning Applied to Document Recognition”।

[৪] ১৯৮৬-র “Learning representations by back-propagatin errors” গবেষণাপত্রটির লেখক David RumelHart, Ronald Williams এবং Geoffrey Hinton।

[৫] ২০১২-র “ImageNet Classification with Deep Convolutional Neural Networks” গবেষণাপত্রটির লেখক Alex Krizhevsky, Ilya Sutskever এবং Geoffrey Hinton।

[৬] একটা অপেক্ষক $x$ নন-লিনিয়ার হবে যদি এইটা সত্যি হয়: $f(x_1 + x_2) \neq f(x_1) + f(x_2)$

[৭] এই বিষয়ে একটা অত্যন্ত মুল্যবান বই হলো এইটা: https://www.deeplearningbook.org/ । বইটা বিনামূল্যে সংগ্রহযোগ্য। এই বইটা পড়লে বিষয়ের একেবারে শিকড়ের কাছাকাছি পৌছনো যাবে। এর একজন লেখক হলেন ইয়ান গুডফেলো, যিনি নিউরাল নেট এবং আরটিফিসিয়াল ইনটেলিজেন্স এর একজন পথিকৃৎও বটে।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.