21-11-2024 10:27:04 am

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

গ্যালিলিও পিসা শহরের মাঝে ভ্যাকুয়াম পেলেন কোত্থেকে ?

অনির্বাণ ঘোষ

("বিজ্ঞান" সম্পাদক)

19 Mar 2021

Link: https://bigyan.org.in/galileo-pisa-vaccum

%e0%a6%97%e0%a7%8d%e0%a6%af%e0%a6%be%e0%a6%b2%e0%a6%bf%e0%a6%b2%e0%a6%bf%e0%a6%93-%e0%a6%aa%e0%a6%bf%e0%a6%b8%e0%a6%be-%e0%a6%b6%e0%a6%b9%e0%a6%b0%e0%a7%87%e0%a6%b0-%e0%a6%ae%e0%a6%be%e0%a6%9d

গ্যালিলিও পিসার হেলানো মিনারের উপর থেকে বিভিন্ন ভরের গোলক ফেলে দেখালেন মাধ্যাকর্ষণের জন্য তাদের ত্বরণ সমান। কারণ তারা প্রায় একসাথে মাটি স্পর্শ করে। অর্থাৎ ত্বরণ ভরের উপর নির্ভর করেনা। এই অব্দি শুনে এক ছাত্র প্রশ্ন করলো, স্যার, এই পরীক্ষাটা কি ভ্যাকুয়াম-এ করা হলো? নইলে তো আলাদা ভরের উপর বায়ুর প্রতিরোধ আলাদা হওয়ার কথা (বায়ুর কারণেই পাখীর পালক ভাসতে ভাসতে পড়ে, আর ভারী জিনিস পড়ে সরাসরি)। এইরকম প্রশ্নের উত্তর সহজ কিছু অঙ্ক কষে (আর একটু গুগল সার্চ করে) কীভাবে দেওয়া যায়, তার একটা উপায় এখানে বাতলানো হলো।

প্রশ্ন

শোনা যায় গ্যালিলিও আলাদা ভরের দুটি গোলক ইতালির পিসা শহরের বিখ্যাত হেলানো মিনারের শীর্ষ থেকে একসঙ্গে ছেড়ে দেন। মিনারের নিচে দাঁড়ানো দর্শকরা অবাক হয়ে দেখেন ভারী এবং হালকা গোলক দুটি প্রায় একসঙ্গে নামতে থাকে এবং প্রায় একসঙ্গে এসে মাটি স্পর্শ করে। পরীক্ষাটা এইটা সাব্যস্ত করেছিল যে অভিকর্ষ জনিত ত্বরণ (acceleration due to gravity) যে কোনো বস্তুর ক্ষেত্রেই সমান।

এই বর্ণনা পড়ে মনে হয় পরীক্ষাটা খোলা হাওয়ায় করা হয়েছিল, বায়ুশূন্য স্থানে নয়। সেক্ষেত্রে গোলকদুটির ওপর পৃথিবীর অভিকর্ষ ছাড়াও বায়ুর বাধাজনিত বল কাজ করছিলো। আমরা জানি ভারী বস্তু বেশি সহজে বায়ুর বাধা অতিক্রম করতে পারে হালকা বস্তুর তুলনায়। ঠিক যে কারণে একই আকারের কয়েন ও শোলার টুকরো সমান উচ্চতা থেকে ফেললে কয়েনটা আগে মাটিতে পৌঁছয়। তাহলে গ্যালিলিওর পরীক্ষায় হালকা গোলকটার বায়ুর বাধা অতিক্রম করে মাটিতে পড়তে অপেক্ষাকৃত বেশি সময় লাগলো না কেন?

আলোচনা

মজার ব্যাপার হলো গ্যালিলিওর নিজের লেখায় পিসা শহরের হেলানো মিনারের কোনো উল্লেখ নেই। তাঁর লেখায় দেখা যায় [1] যে তিনি উঁচু স্থান থেকে আলাদা আলাদা ভরসম্পন্ন বস্তুপিন্ড ফেলে দেখেছেন যে তারা প্রায় একসাথে মাটি স্পর্শ করে। কত উচ্চতা, ঠিক কী আকারের বস্তুপিন্ড, তার উপাদান কী, ভর কত, সেই নিয়ে সঠিক তথ্য তাঁর লেখায় পাওয়া যায় না।

তাই এই আলোচনায় আমরা নিজেদের মতো করে একটা পরীক্ষা কল্পনা করবো যেখানে একই মাপের একটা লোহার আর একটা কাঠের গোলক। অর্থাৎ দুটোর ব্যাসার্ধ সমান, ধরা যাক:

$R = 5 \hspace{1mm} \mathrm{cm}$

একসাথে ফেলা হচ্ছে উচ্চতা

$H = 1.5 \hspace{1mm} \mathrm{m}$

থেকে। দেখা যাক, বায়ুর বাধাকে ধরলে এদের পতনে তফাৎ হয় কিনা।

পতনের সময় গোলকটির ওপর দু’ধরণের বল কাজ করে:

পৃথিবীর অভিকর্ষ বল

আমরা স্কুলে বিজ্ঞানের ক্লাসে শিখেছি যে এই বলের প্রভাবে গোলকটির

$g= 9.8 \hspace{1mm} \mathrm{m/s^2}$

নিম্নমুখী ত্বরণ হয়।

বায়ুর বাধাজনিত বল

এই ঊর্ধ্বমুখী বল গোলককে নীচে পড়তে বাধা দেয়। একটু খুঁটিয়ে দেখলে, এই বলের আবার দুটো অংশ আছে :

প্রথমত, গোলকটা কিছুটা বাতাসকে সরিয়ে দিয়ে জায়গা দখল করে বসেছে। আর্কিমিডিসের সূত্র অনুযায়ী, ঠিক যতটা বাতাস সরিয়েছে তার ওজনের সমান একটা উর্দ্ধমুখী বল গোলকটার ওপর কাজ করে। এই বলের নাম প্লবতা (buoyant force) এবং গোলকটি পড়ার সাথে সাথে এর মান পাল্টায় না।
দ্বিতীয়ত, চলন্ত গোলকের উপরিতলের সাথে বায়ুর ঘর্ষণবল-ও পতনের বিরোধিতা করে। একে আমরা পিছুটান (drag force) বলতে পারি। এই বল কিন্তু গোলকটি পড়ার সাথে সাথে পাল্টায়। গোলকটি স্থির থাকলে এই বলের পরিমাণ শূন্য। গোলকের গতি যত বাড়তে থাকে এই পিছুটান-ও পাল্লা দিয়ে বাড়তে থাকে।

এই দু’রকম ঊর্ধ্বমুখী বলের প্রভাবে গোলকটির ত্বরণের নাম দেওয়া যায় যথাক্রমে $a_{buoyant}$ এবং $a_{drag}$ । আমাদের মূল প্রশ্নের উত্তর দিতে হলে অভিকর্ষ ত্বরণ $g$ এর সাথে $a_{buoyant}$ এবং $a_{drag}$ এদেরকে তুলনা করতে হবে। এই তুলনা করার সবচেয়ে সোজা উপায় হলো

$\frac{a_{buoyant}}{g}$

এবং

$\frac{a_{drag}}{g}$

এই অনুপাত দুটো গণনা করা। এই অনুপাত দুটোকে যদি গোলকের কিছু বৈশিষ্ট্যের (যেমন তার ব্যাসার্ধ $R$ বা উপাদানের ঘনত্ব $\rho_{ball}$ ) মাধ্যমে প্রকাশ করা যায়, তাহলে গোলক দেখেই বলে দেওয়া যাবে এই অনুপাতগুলো খুব ছোট না বড়। অর্থাৎ, বায়ুর বাধাকে ধর্তব্যে আনা উচিত কি না। এই গণনাটাই আমরা এবার করবো।

বাধা নাম্বার ওয়ান : প্লবতা

আর্কিমিডিসের সূত্র অনুযায়ী এই বল উপরের দিকে কাজ করে, অর্থাৎ গোলককে নিচে পড়তে বাধা দেয়। বাতাসের ঘনত্ব যদি $\rho_{air}$ হয় তাহলে উর্ধমুখী প্লবতা বলের পরিমাণ

$F_{buoyant} = \rho_{air}Vg$ ,

যেখানে $V = \frac{4}{3}\pi R^3$ হলো গোলকটির আয়তন।

গোলকটির উপাদানের ঘনত্ব যদি $\rho_{ball}$ হয় তাহলে তার ভর $M_{ball} = \rho_{air}Vg$ । নিউটনের দ্বিতীয় গতিসূত্র প্রয়োগ করে গোলকটির প্লবতাজনিত ঊর্ধ্বমুখী ত্বরণের মান পাওয়া যায়:

$a_{buoyant} = \frac{F_{buoyant}}{M_{ball}} = \frac{\rho_{air}Vg}{\rho_{ball}V} = \frac{\rho_{air}}{\rho_{ball}}g$

$\implies \frac{a_{buoyant}}{g} = \frac{\rho_{air}}{\rho_{ball}}$

অর্থাৎ গোলকের উপাদানের (কাঠ বা লোহা) তুলনায় বাতাস যত গুণ হালকা, প্লবতাজনিত ত্বরণও অভিকর্ষজ ত্বরণের তুলনায় তত গুণ কম হবে! সমীকরণে $\rho_{air}$ এবং $\rho_{ball}$ -এর মান বসানোর আগেই নিশ্চই আন্দাজ করতে পারছ যে আমাদের পরীক্ষায় প্লবতা বলের প্রভাব সম্ভবতঃ উপেক্ষণীয়।

নিজে করো: কাঠের ঘনত্বের মান ওপরের সমীকরণে বসিয়ে দেখো $a_{buoyant, wood}$ ঠিক কত হয়। $a_{buoyant, wood}$ -এর প্রভাবে আমাদের পরীক্ষার ফলে কোনো পরিমাপযোগ্য তারতম্য হবে কি ?

বাধা নাম্বার টু: পিছুটান

বায়ুগতিবিদ্যার (aerodynamics) গবেষকরা নির্ণয় করেছেন যে বস্তুপিণ্ডের গতি $v$ যত বাড়ে, বাতাসের ঘর্ষণজনিত পিছুটান বলও তত বাড়তে থাকে এই সমীকরণ অনুযায়ী:

$F_{drag} = \frac{1}{2}C_{D}\rho_{air}Av^2$

যেখানে:

$A$ হলো গতি $v$ -এর উল্লম্বতলে বস্তুপিণ্ডটির প্রস্থচ্ছেদ। অর্থাৎ, গোলকের ক্ষেত্রে $A = \pi R^2$ .
$C_{D}$ একটি রাশি যার মান বস্তুপিণ্ডের আকার, গতি, এবং বায়ুর সান্দ্রতা সহগের (coefficient of viscosity) ওপর নির্ভর করে। গোলকাকৃতি বস্তু এবং আমরা যে ধরণের গতি নিয়ে কাজ করছি তার জন্য এর মান মোটামুটিভাবে $0.1$ থেকে $0.5$ এর মধ্যে হয় [2]।

আমরা আগের প্লবতা নিয়ে আলোচনার সূত্র ধরে পিছুটান $F_{drag}$ -এর জন্য গোলকের ত্বরণ

$a_{drag} = \frac{F_{drag}}{M_{ball}}$

গণনা করার চেষ্টা করবো, এবং বোঝার চেষ্টা করবো যে $a_{drag}$ -এর প্রভাবে আমাদের পরীক্ষার ফলের পরিমাপযোগ্য তারতম্য হবে কিনা।

প্রথমেই লক্ষ্য করো যে প্লবতা এবং পিছুটানের একটা প্রধান পার্থক্য হলো যে একটা বিশেষ গোলকের জন্যে $F_{buoyant}$ একটা ধ্রুবক, কিন্তু $F_{drag}$ গোলকের গতির ওপর নির্ভর করে। যখন গোলকটি সবে ছেড়েছি তখন তার গতি প্রায় শূন্য, সুতরাং তার ওপর প্রযুক্ত পিছুটানও প্রায় শূন্য। গোলকটি যখন প্রায় মাটি স্পর্শ করছে, তখন তার ওপর পিছুটান সবথেকে বেশি।

এই ধরণের পরিবর্তনশীল বল নিয়ে গণনা করা বেশ কঠিন, তাই শুরুতে গণনা সহজতর করার জন্য আমরা $F_{drag}$ -এর সর্বোচ্চ সীমা (যা একটি ধ্রুবক $F_{drag,max}$ ) নিয়ে কাজ করতে পারি। যদি এই সর্বোচ্চ সীমার প্রভাব-ও অভিকর্ষের তুলনায় উপক্ষেণীয় হয়, তাহলে আসল বলটার-ও তাই হবে। যদি না হয়, তখন সীমা-টীমা ভুলে আসল বলটা নিয়ে কাজ করতে হবে।

অঙ্কটা করে দেখা যাক। পিছুটানের সর্বোচ্চ সীমার জন্য ত্বরণের মান:

$a_{drag} = \frac{F_{drag,max}}{m_{ball}} = \frac{\frac{1}{2}C_{D,max}\rho_{air}Av_{max}^2}{\rho_{ball}V}$

সমীকরণের ডানপার্শ্বের রাশিগুলির মান একে একে নির্ণয় করা যাক।

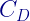$C_{D}$ -এর মান :

আগেই বলা হয়েছে আমরা যে ধরণের গতি নিয়ে কাজ করছি তার জন্য $C_{D}$ -এর মান মোটামুটিভাবে $0.1$ থেকে $0.5$ এর মধ্যে হয় [2]। সুতরাং

$C_{D,max} = \frac{1}{2}$ .

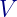$V$ আর $A$ -এর মান :

গতি $v$ -এর উল্লম্বতলে গোলকটির প্রস্থচ্ছেদ $A = \pi R^2$ । গোলকটির আয়তন হলো

$V = \frac{4}{3}\pi R^3$

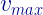$v_{max}$ -এর মান :

গোলকটি ফেলা হচ্ছে $H$ উচ্চতা থেকে। বায়ুশূন্য স্থানে $H$ উচ্চতা থেকে পতন ঘটলে গোলকটির সর্বোচ্চ গতি হতো:

$v_{0}^2 - 0^2 = 2gH \implies v_{0} = \sqrt{2gH}$

বায়ুর পিছুটান থাকলে সর্বোচ্চ গতি $v_{0}$ -এর থেকে একটু কমই হবে। তাই গতির সর্বোচ্চ সীমা $v_{max}$ -এর জায়গায় আমরা $v_{0}$ -এর মানই ব্যবহার করতে পারি:

$v_{max} = v_{0} = \sqrt{2gH}$

সব মানগুলোকে বসালে :

এই মানগুলো বসিয়ে পাই:

$\frac{a_{drag,max}}{g} = \frac{3}{8}\frac{H}{R}\frac{\rho_{air}}{\rho_{ball}}$

এটা বেশ একটা সুন্দর সমীকরণ কারণ এর থেকে পিছুটানের প্রভাবের একটা পরিষ্কার ছবি পাওয়া যাচ্ছে। সামনের $\frac{3}{8}$ গুণিতকটা ভুলে গেলে মোটামুটিভাবে বলা যায় যে মাটি স্পর্শ করার সময় পিছুটান ও অভিকর্ষের প্রভাব সমান করতে হলে গোলকটির উপাদান বায়ুর থেকে যতগুণ ভারী, গোলকটিকে নিজের ব্যাসার্ধের তুলনায় ঠিক ততগুণ উচ্চতা থেকে ফেলতে হবে ! (মোটামুটি বললাম কারণ এই গণনার মধ্যে কয়েকটা আসন্নায়ন ছিল।) আমাদের পরীক্ষায় কাঠ ও লোহার গোলক ব্যবহার করেছি আমরা। কাঠ লোহার থেকে অনেক হালকা, তাই প্রথমে কাঠের গোলকের জন্য $\frac{a_{drag,max}}{g}$ বের করা যাক। গুগল সার্চ করে ঘনত্বের মান খুঁজলে দেখতে পাবে যে কাঠ মোটামুটিভাবে বাতাসের থেকে পাচঁশোগুণ ভারী। সুতরাং,

$\frac{a_{drag,max,wood}}{g} = \frac{3}{8}\frac{1.5}{0.05}\frac{1}{500} \approx \frac{1}{40}$

লোহা বায়ুর তুলনায় আরও অনেক ভারী (7300 গুণের কাছাকাছি)। সুতরাং লোহার ক্ষেত্রে পিছুটানের প্রভাব কাঠের থেকেও চোদ্দ-পনেরো গুণ কম হবে।

নিজে করো: $a_{drag.max.wood}$ এবং $a_{buoyant.wood}$ -এর অনুপাত কত? $a.{drag.max.wood}$ -এর প্রভাবে আমাদের কল্পিত পরীক্ষার ফলে কোনো পরিমাপযোগ্য তারতম্য হবে কি ?

উত্তর

নিশ্চয় দেখলে যে উপরের দুটো “নিজে করো” প্রশ্নেরই উত্তর “না”। সুতরাং আমাদের পরীক্ষা বায়ুশূন্য স্থানে না করা হলেও এর ওপর বায়ুর প্রভাব উপেক্ষণীয় এবং দুটো গোলকই প্রায় একসাথে মাটি স্পর্শ করবে। এর থেকে অনুমান করা যায় যে গ্যালিলিও যদি আরও অনেক উঁচু ( $H_{Galileo}$ ) কোনো স্থান থেকে আরও অনেক বড়ো ব্যাসার্ধ ( $R_{Galileo}$ ) ওয়ালা দুটো গোলক ফেলেও থাকেন, তাঁর ক্ষেত্রে $\frac{H_{Galileo}}{R_{Galileo}}$ -এর মান আমাদের মতোই কিছু একটা ছিল। যে কারণে ওঁর পরীক্ষাতেও বায়ুর বাধা হয়তো বিশেষ প্রভাব ফেলেনি।

(এক ছাত্রের প্রশ্ন আমাদের কাছে পৌঁছে দেওয়ার জন্য কাঁথির শ্রেয়ম জানা-কে অসংখ্য ধন্যবাদ জানাই। আপনি যদি ইস্কুলের শিক্ষক বা শিক্ষিকা হন এবং আপনার ছাত্র বা ছাত্রী যদি কোনো প্রশ্ন করে যার উত্তর হয়তো আপনিও জানতে চান, নির্দ্বিধায় আমাদের ই-মেল করুন [email protected]এ।)

(প্রচ্ছদের ছবির সূত্র)

[1] https://en.wikipedia.org/wiki/Galileo_Galilei#Falling_bodies

[2] https://www.grc.nasa.gov/www/k-12/airplane/dragsphere.html

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।