গড়িয়ে চলার সময় ঘর্ষণ (ঘর্ষণের উৎস - পর্ব ৩)

সৌরভ কান্তি দে

(মিরগোদা মৃত্যুঞ্জয় বাণীপীঠ)

 

প্রদীপ্ত পঞ্চাধ্যায়ী

(কাঁথি প্রভাত কুমার কলেজ)

 

10 Dec 2021

Link: https://bigyan.org.in/friction-advantage-disadvantage-part-03

বাজার করে এসে মামা বসলেন কাটা তরমুজ নিয়ে। বারান্দা থেকে মামার সাইকেলটা দেখা–ই যাচ্ছিলো। তা দেখে মামা ভাবালু হয়ে গেলেন –

মামা: একটা জিনিস ঘষতে ঘষতে নিয়ে গেলে তো উল্টোদিকে ঘর্ষণ কাজ করে, গড়াতে গড়াতে নিয়ে গেলেও কি একইরকম ঘর্ষণ কাজ করবে?

ভাগ্নে: গড়াতে গড়াতে মানে কিরকম বলছো?

দাঁড়া, তোকে একটা উদাহরণ দি।

গড়িয়ে চলা মানে কি

সার্কাসের এক চাকার সাইকেলের কথা মনে পড়ছে? গতবছর মেলায় যেটা দেখেছিলি?

হ্যাঁ মামা!

মনে কর ঐরম একটা চাকা সমতলে এগিয়ে যাচ্ছে। ধর, প্যাডেল করে চাকাটাকে ক্রমশ জোরে ঘোরাচ্ছি, অর্থাৎ চাকাটার কৌণিক গতি বাড়াচ্ছি। কৌণিক গতি বুঝিস?

কৌণিক গতি মানে সেকেন্ডে চাকাটা কতটা কোণে ঘুরবে?

ঠিক। আমি ক্রমশ জোরে প্যাডেল করছি মানে চাকাটার কৌণিক গতিও বাড়ছে।

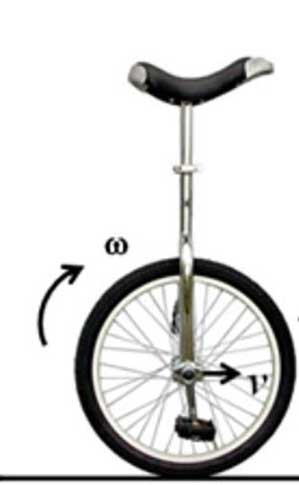
বুঝলাম। তুমি প্যাডেল করছো আর চাকাটা গড়াচ্ছে? এটাই গড়ানো?

হ্যাঁ, কিন্তু গড়ানো ব্যাপারটার একটা বিশেষ মানে আছে। যখন আমি না পিছলে গড়ানোর কথা বলি, ইংরাজিতে যেটাকে বলে rolling without slipping, সেটার মানে হলো, চাকাটার যে বিন্দুটা মাটির সাথে লেগে আছে, ঠিক সেই বিন্দুতে গতি শূন্য। চাকা যতই জোরেই এগোক না কেন, ঠিক ওই জায়গাটাতে গতি শূন্য। অর্থাৎ চাকাটা একটুও ঘষ্টাচ্ছে না মাটিতে।

চাকাটা তো এগোচ্ছে, তাহলে গতি শূন্য কিভাবে হয়?

গোটা চাকাটার গতি শূন্য না, শুধু যে বিন্দুটা মাটিতে লেগে আছে, সেইখানটা। নিচের ছবিতে যেটা বিন্দু, সেখানটার কথা বলছি। গোটা চাকাটা সাইকেলের সাথে সাথে এগোচ্ছে সামনের দিকে, আর চাকাটা ঘোরার ফলে চাকার নিচের অংশটা যাচ্ছে পিছনের দিকে। দুইয়ে কাটাকুটি হওয়ার ফলে চাকাটার যত নিচে যাচ্ছি, গতিটা একটু একটু করে কমছে। কমতে কমতে যদি একদম মাটির সাথে লেগে থাকা বিন্দুটা দেখি, ওটা “না পিছলে গড়ানোর সময়” কিন্তু মুহূর্তের জন্য একদম থেমে গেছে। ছবি এঁকে অঙ্কের ভাষায় বোঝাই তোকে।

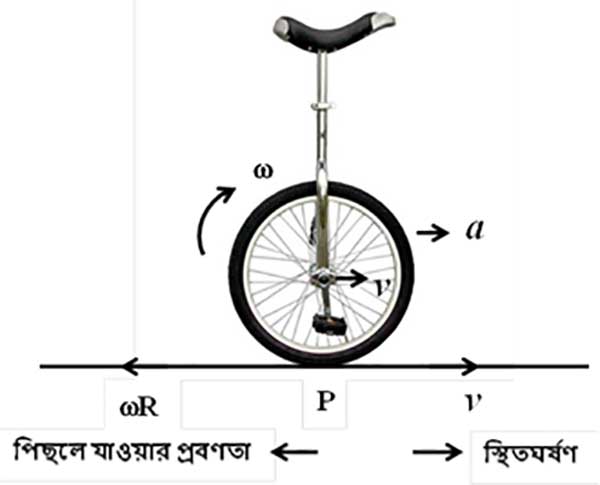
এই ছবিটা দেখ। ধর, যেকোনো একটা মুহূর্তে চাকার ভরকেন্দ্রের গতিবেগ , কৌণিক বেগ  আর চাকার ব্যাসার্ধ । যেখানে চাকাটা মাটিতে ঠেকছে, অর্থাৎ ছবিতে বিন্দুটা, সেইখানটার গতি তাহলে হবে । কেন, সেটা বুঝতে পারলি?

বোধহয় পেরেছি। যদি চাকার কৌণিক বেগ  হয়, তাহলে চাকাটার সবথেকে নিচের বিন্দুতে স্পর্শক (tangent) বরাবর একটা  গতি থাকবে। সাইকেল যেদিকে  বেগে এগোচ্ছে, চাকার নিচের বিন্দুর  গতিটা তার উল্টোদিকে হবে। অতএব ওই নিচের বিন্দুটাতে নিট গতিটা পেতে তুমি  থেকে -কে বাদ দিলে।

একদম ঠিক। এবার যদি চাকাটা যাকে বলে “না পিছলে শুধু গড়িয়ে যায়”,  আর  সমান হবে। অর্থাৎ, চাকাটা যেখানে মাটিতে ঠেকছে, ঠিক সেখানে তাৎক্ষণিকভাবে  গতিটা শূন্য।

আচ্ছা, তুমি গড়ানোর সময় চাকার উপর ঘর্ষণের কথা জিজ্ঞেস করছিলে। মাটিতে ঠেকে থাকা বিন্দুটার গতি শূন্য মানে কি তার উল্টোদিকে কোনো ঘর্ষণ নেই?

গতি শূন্য মানেই যে ঘর্ষণ নেই, এমন তো নয়। এর আগে যে স্থির অবস্থার ঘর্ষণের কথা বললাম, সেখানে কি শিখলি?

ওহ হ্যাঁ, তুমি বলেছিলে বটে, গতির দরকার নেই, গতির প্রবণতা থাকলেই চলবে। অর্থাৎ, এখানে কি স্থিতঘর্ষণ বা static friction কাজ করছে?

একদম ঠিক! কেন সেটা হচ্ছে, এটা বুঝতে একটু ভাবতে হবে। দেখ, আমি কিন্তু ক্রমশ জোরে প্যাডেল করছি। তাই, প্রত্যেক মুহূর্তে  আর  সমান হলেও আমার ক্রমশ জোরে প্যাডেল করার ফলে যেটা হচ্ছে, সেটাকে এইভাবে ভাবতে পারিস – চাকার কৌণিক গতি  এবং ফলে  একটু বাড়ছে, এবং পরমুহূর্তেই -ও একটু বাড়ছে। অতএব যতই  শূন্য রয়ে যাক, মুহূর্তের জন্য চাকাটার পিছনের দিকে পিছলে যাওয়ার একটা প্রবণতা থেকে যাচ্ছে। তুই নিশ্চয়ই খেয়াল করেছিস জলকাদায় বালির উপর সাইকেল চালানোর সময় পেছনের দিকে জল-কাদা, বালি ছি্টকে আসে। ওটা হয় চাকা ঐ পেছনের দিকে পিছলে যেতে চায় বলেই। যেহেতু এই পিছলে যাওয়ার প্রবণতা রয়েছে, ওটাকে আটকাতে স্থিত ঘর্ষণ সামনের দিকে কাজ করছে।

আরেকভাবেও ব্যাপারটা ভাবতে পারিস। ধর, ঘর্ষণ একদমই নেই। তখন প্যাডেল করলে কি হতো? চাকার একদম নিচের বিন্দুটা বিনা বাধায় পিছনের দিকে যেত। স্থিতঘর্ষণ যেহেতু স্পর্শবিন্দুর গতিকে আটকায়, ওটা কাজ করছে সামনের দিকে।

আচ্ছা, এই স্থিত ঘর্ষণের মান কত বলতে পারবি? ধর, যদি সাইকেলের ত্বরণ হয়  আর ভর হয় ।

কিভাবে বলবো?

দেখ, শুধু চাকাটার কথা ভাবলে স্থিতঘর্ষণ চাকাটাকে পিছলে যাওয়া থেকে আটকাচ্ছে। কিন্তু চালকসুদ্ধ সাইকেলটাকে যদি ধরিস, ওর উপর জমি থেকে কিন্তু খালি একটাই বল কাজ করছে। সেটাও ওই স্থিত ঘর্ষণ। ওটাই চাকাটাকে সামনে এগিয়ে দিচ্ছে। আর কোনো বল কিন্তু নেই সামনের দিকে। অতএব, ওই স্থিত ঘর্ষণের মান নিউটনের সূত্র অনুযায়ী হবে ।

দারুণ ব্যাপার তো। আচ্ছা মামা দু–চাকা সাইকেল, মানে তোমার আমার সাইকেলের ক্ষেত্রেও কি এইরকম হয় ?

সাইকেলের পেছনের চাকায় ঠিক এরকমটাই ঘটে, কারণ পেছনের চাকা প্যাডেলের সাথে যুক্ত থাকে (নিচের ছবিটা দেখ)। অতএব ওটা ওই একচাকা সাইকেলের মতই।

সাইকেলের পিছনের চাকা প্যাডেলে ঘোরে, সামনেরটাকে ঘোরায় কে?

কিন্তু সামনের চাকায় অন্যরকম ঘটে। সামনের চাকাটা যেহেতু বাকি সাইকেলটার সাথে লেগে আছে, সাইকেল যত এগোয়, সামনের চাকাটাও এগোনোর চেষ্টা করে। ঘর্ষণ না থাকলে বিনা বাধায় এগোতোও। এক কথায়, চাকাটার সামনের দিকে এগোনোর একটা প্রবণতা থাকে। তাই সেটাকে আটকাতে সামনের চাকায় ঘর্ষণ কাজ করে পিছনের দিকে। যদি সামনের চাকাটাও না পিছলে এগোয়, তাহলে এই ঘর্ষণটাও স্থিতঘর্ষণ। অর্থাৎ, দুটো চাকাই না পিছলে গড়াচ্ছে আর দুটোতেই স্থিতঘর্ষণ কাজ করছে। পিছনের চাকায় ঘর্ষণটা সামনের দিকে আর সামনের চাকায় পিছনের দিকে।

মনে কর, পেছনের চাকায় স্থিতঘর্ষণ বল  আর সামনের চাকায় স্থিতঘর্ষণ বল । চালকসুদ্ধ সাইকেলের উপর কিন্তু জমির থেকে সর্বসাকুল্যে সাইকেলের গতির দিকে বা বিরুদ্ধে এই দুটো বলই রয়েছে। অতএব, সাইকেলটাকে যদি ক্রমশ জোরে চলতে হয়, পেছনের চাকার উপর স্থিতঘর্ষণটাকে সামনেরটার থেকে বেশি হতে হবে। অর্থাৎ  । দুইয়ের বিয়োগফল নিলে বেরোবে কতটা বল রয়েছে সামনের দিকে। অর্থাৎ:

এবার গোটা সাইকেল ছেড়ে শুধু সামনের চাকাটার গোল গোল ঘোরার কথা ভাব। পেছনের চাকায় নাহয় আরো জোরে প্যাডেল করে কৌণিক বেগ বাড়াচ্ছি। কিন্তু সামনের চাকায় তো প্যাডেল নেই, তাহলে সেটা আরো জোরে ঘুরছে কিভাবে?

ভাবছি মাঝখানে আটকে থাকা একটা চাকাকে জোরে ঘোরাতে কি লাগে।

ঠিক শুরু করেছিস। কি লাগে?

চাকার সাইডে হাত দিয়ে জোরে সেটাকে ঘুরিয়ে দিতে পারি। ঘড়ির কাঁটা যেদিকে ঘোরে (clockwise) বা তার উল্টোদিকে (anticlockwise)।

অর্থাৎ চাকার সাইডে একটা বল প্রয়োগ করছিস। যেহেতু চাকাটা মাঝে আটকে, এক্ষেত্রে বলটা চাকাটাকে সরাচ্ছে না, শুধু ঘোরাচ্ছে। এই ঘোরানোর প্রবৃত্তিটাকে বলে টর্ক (torque)। এবার বল, সাইকেলের সামনের চাকাটার সাইডে সেই বলটা আসছে কোত্থেকে?

একটাই তো বল রয়েছে ওই চাকার উপর, স্থিত ঘর্ষণ। সেটাই তাহলে সামনের চাকাটাকে ক্রমশ জোরে ঘোরাচ্ছে।

সাব্বাশ! এবার তাহলে তুই বলতে পারবি ব্রেক করার সময় সাইকেলে স্থিতঘর্ষণ কিভাবে কাজ করে?

হ্যাঁ মামা। ঠিক এর উল্টোটা। পিছনের চাকায় স্থিতঘর্ষণ হবে পিছনের দিকে আর সামনের চাকায় সামনের দিকে।

ঠিকই ধরেছিস। কিন্তু এই ব্যাখ্যাটা খাটবে যদি শুধুমাত্র পেছনের চাকায় ব্রেক কষা হয়। একই সাথে সামনে পেছনে দুটো চাকায় ব্রেক কষলে ব্যাপারটা একটু অন্যরকম দাঁড়ায়। সেক্ষেত্রে দুটো চাকায় স্থিতঘর্ষণ পেছনের দিকে অর্থাৎ সাইকেলের গতির উল্টোদিকে কাজ করে। যাক দু ক্ষেত্রে ব্রেক করার এই দুরকম ব্যাপার পরে গুছিয়ে সুন্দর করে লিখে দেখাবি।

ঠিক আছে। আচ্ছা মামা, একটা জিনিস ভাবছিলাম। যদি প্যাডেল করা বন্ধ করে দি, ব্রেকও না কষি, তাহলে তো কোনোরকম স্থিতঘর্ষণও থাকার কথা না। কারণ ক্রমাগত জোরে প্যাডেল না করলে তো চাকার গতিও বাড়বে না, পিছলে যাওয়ার কোনো প্রবণতাও থাকবে না। তাহলে একবার স্পীড তুললে সাইকেল সুন্দর বিনা ঘর্ষণে দিব্যি চলতে পারে। চলেও অনেকদূর, কিন্তু অনন্তকাল চলেনা কেন?

খুব ভালো প্রশ্ন। আসলে আমি একটা আদর্শ ব্যাপার নিয়ে আলোচনা করলাম। এই আদর্শ অবস্থায় তোর কথাটা ঠিক। সাইকেলের স্পিড একবার তুললে সেটা অনন্তকাল চলতে পারে। বাস্তবে আরেকটা প্যাঁচ আছে।

প্যাডেল না করে সাইকেল অনন্তকাল চালানো যায়না কেন

কিরকম আদর্শ ব্যাপার?

ওই যে বললাম, চাকার যে বিন্দুটা জমিতে ঠেকছে, তার গতি শূন্য। খেয়াল করে দেখ, বিন্দুটা বলছি। একটাই বিন্দুতে চাকাটা জমিতে ঠেকছে। এই ব্যাপারটা চাকা, জমি দুটোই আদর্শ দৃঢ় বস্তু (ideal rigid body) হলে তবেই হবে।

একটাই বিন্দুতে ঠেকছে তো কি হয়েছে?

একটাই বিন্দুতে লেগে থাকলে জমির লম্ব প্রতিক্রিয়া এই ছবিটার মত হয়।

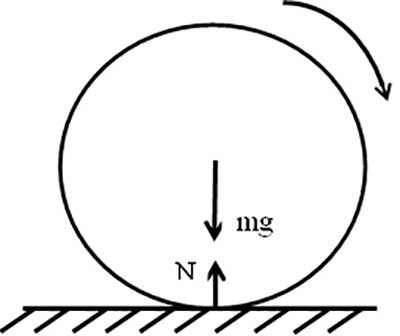
এই লম্ব প্রতিক্রিয়ার কোনও অনুভুমিক উপাংশ (horizontal component) থাকে না। অর্থাৎ ওটার থেকে চাকার গতিতে কোনো বাধা আসেনা। আর যেহেতু এই লম্ব প্রতিক্রিয়া চাকার ঠিক মাঝখান দিয়ে যায়, এটা চাকাটার ঘোরাতেও কোনো বাধা দেয় না। এক কথায়, চাকার ঘোরার কথা ভাবতে গেলে লম্ব প্রতিক্রিয়াটাকে ধর্তব্যের মধ্যে আনারই দরকার নেই।

আচ্ছা, এটা নাহয় আদর্শ ব্যাপার হলো। বাস্তবে কি হয়?

বাস্তবে কিন্তু কোনও বস্তুই সম্পূর্ণভাবে দৃঢ় নয়। ফলে চাকা ও ভূমি একটা বিন্দুর পরিবর্তে অনেকটা জায়গা জুড়ে পরস্পরকে স্পর্শ করে। অর্থাৎ অনেকগুলো বিন্দুতে তারা লেগে থাকে। খানিকটা এই ছবিটার মত।

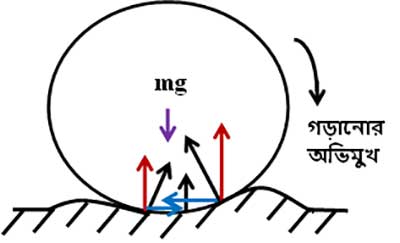
একটা জিনিস লক্ষ্য কর, চাকাটা যেহেতু সামনে এগোচ্ছে, ওটা সামনের দিকে অনেকটা বেশি চেপে বসে আছে, পিছনের দিকটার তুলনায়। ছবিতে সামনের আর পিছনের অংশ থেকে লম্ব প্রতিক্রিয়াটাকে দেখালাম। চাকাটা সামনে বেশি চেপে থাকার ফলে সেখানকার লম্ব প্রতিক্রিয়ার ভেক্টর-টাকে একটু বড় দেখালাম।

এবার এই দুদিকের প্রতিক্রিয়ার উপাংশগুলোকে (component) দেখা যাক। দুটোরই উল্লম্ব উপাংশ (vertical component) উপরের দিকে। কিন্তু অনুভূমিক উপাংশগুলো (horizontal component) একে অপরের উল্টোদিকে। সামনের অংশ থেকে আসা প্রতিক্রিয়ার অনুভূমিক উপাংশ চাকার গতির বিরোধিতা করে আর পিছনের অংশ থেকে একই জিনিস চাকার গতির সহযোগিতা করে। কিন্তু, প্রথমটা দ্বিতীয়টার চেয়ে বেশি কারণ, ওই যে বললাম, চাকা সামনে একটু বেশি চেপে বসেছে।

তার মানে এই চেপে বসার ফলে চাকার গতির বিরুদ্ধে একটা নিট বল কাজ করছে? আর সেটাই চাকাটাকে থামিয়ে দিচ্ছে?

একদম ঠিক! এটাকেও এক ধরণের ঘর্ষণ বলা যায়। এটা ঠিক আগের মতো স্থিতঘর্ষণ (static friction) বা চলঘর্ষণ (kinetic friction) নয় কারণ দুটোই এক্ষেত্রে শূন্য। এটাকে আবর্ত ঘর্ষণ (rolling friction) নাম দেওয়া হয়।

চাকার এই ধীরে ধীরে থেমে যাওয়াটাকে কি টর্ক (torque) দিয়েও ব্যাখ্যা করতে পারো? তোমার ছবি দেখে মনে হচ্ছে, দুটো উল্লম্ব উপাংশ (vertical component) বিপরীত দিকে টর্ক দিচ্ছে।

সেটাও লক্ষ্য করেছিস! দারুণ তো! হ্যাঁ, একদম ঠিক। ছবিটা একটু পাল্টে সবকটা টর্ক দেখাই তোকে। দেখ, আবর্ত ঘর্ষণ আর পিছনের দিকের প্রতিক্রিয়ার উল্লম্ব উপাংশ, এগুলো ঘড়ির কাঁটার দিকে টর্ক দিচ্ছে। কিন্তু সামনের দিকের প্রতিক্রিয়ার উল্লম্ব উপাংশ ঘড়ির কাঁটার উল্টোদিকে টর্ক দিচ্ছে। আর যেহেতু ওটা বেশি, তাই ধীরে ধীরে ওটা চাকার ঘোরার গতিটাও কমিয়ে দিচ্ছে।

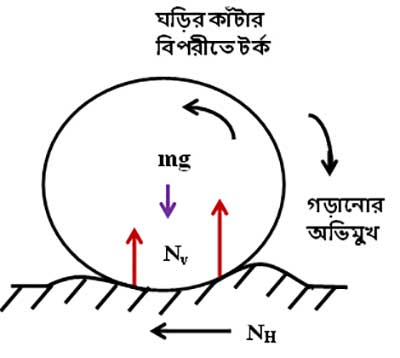
অর্থাৎ, যেভাবেই ভাবিস না কেন, চাকাটার সামনের দিকটা জমিতে একটু দেবে থাকার ফলে প্যাডেল বন্ধ করার পর আস্তে আস্তে তার গতিটা কমতে থাকে।  অনন্তকাল ওটা চলতে পারেনা।

সাইকেলে চড়াই উৎরাই পেরোনো

হ্যাঁ এবার বুঝতে পেরেছি। আচ্ছা মামা যদি জমিটা সমতল না হয়ে চড়াই হয়? তখন তো শুধু সাইকেলের উপর ঘর্ষণের কথা ধরলেই চলবে না।

তা ঠিক, কিন্তু সমতলের ক্ষেত্রে যে কথাগুলো বললাম, তার অনেকটাই এখানেও খাটবে। এই ছবিটা দেখ।

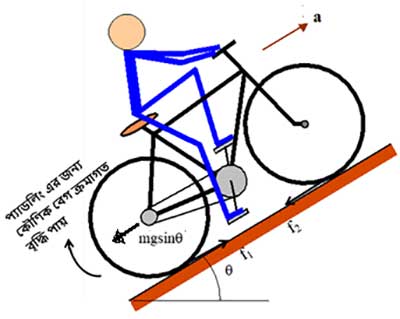
এখানে আগের তুলনায় একটাই অতিরিক্ত বল রয়েছে, সেটা হলো ওজন। সমতলেও ওজন ছিল কিন্তু ওটা চলার দিকে কোনো বল দিচ্ছিল না। এখন চড়াইয়ে ওজনের একটা উপাংশ (component) জমি বরাবর কাজ করবে এবং সাইকেলটাকে নিচে টানার চেষ্টা করবে। চালকসুদ্ধ সাইকেলের ভর যদি হয় , তার ওজন হলো  আর সেই ওজনের উপাংশ হলো , যেখানে  হলো সমতলের সাথে কতটা কোণে সাইকেলটা চলছে।

বাকিটা কিন্তু আগে যা বললাম, সেইরকমই। পিছনের চাকা প্যাডেল করার জন্য পিছনের দিকে পিছলে যেতে চায়, তাই তার উপর স্থিতঘর্ষণ সামনের দিকে। এই ঘর্ষণটাকে বলা যাক । আর সামনের চাকা সাইকেলের সাথে লেগে আছে বলে যেতে চায় সামনের দিকে, তাই তার উপর স্থিতঘর্ষণ পিছনের দিকে। এই ঘর্ষণটাকে বলা যাক । তাহলে সাইকেলের ত্বরণ (acceleration) যদি হয় , সমতলের সমীকরণটা তাহলে সামান্য পাল্টে গিয়ে হয়:

যদি টর্কের কথা ভাবিস, তাহলে কিন্তু ওজনটাকে ধরারও দরকার নেই কারণ সেটা চাকার কেন্দ্র দিয়ে যায়। অর্থাৎ, সমতলের মতোই পিছনের চাকাটা আরো জোরে ঘুরছে কারণ তুই প্যাডেল করছিস, আর সামনের চাকাটা আরো জোরে ঘুরছে কারণ স্থিতঘর্ষণের থেকে একটা টর্ক আসছে।

কিন্তু মামা, চড়াইয়ে যদি সাইকেলটাকে একই স্পীডে চালাতে চাই, তাহলেও তো প্যাডেল করে যেতে হবে। এইটা কি ওজনের পিছুটানের জন্যেই?

একদম ঠিক। সমতলে যদি তুই স্পীড না বাড়াস, তাহলে চাকার পিছলে যাওয়ারও প্রশ্ন নেই, কোনোরকম ঘর্ষণও নেই (আদর্শ কেস-টার কথা হচ্ছে)। কিন্তু চড়াইয়ে ওজনের পিছুটানের জন্য সাইকেল নিচে যেতে চায়, তাই তাকে আটকাতে দুটো চাকাতেই সামনের দিকে একটা ঘর্ষণ কাজ করবে। এটা ঘড়ির কাঁটার বিপরীতে একটা টর্ক দিয়ে চাকাদুটোর ঘোরাকে স্লো করে দেবে, তাই স্পীড বজায় রাখতে গেলে তোকে ক্রমাগত প্যাডেল করে যেতে হবে।

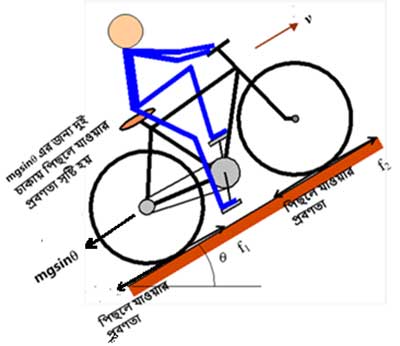
এবার একটা মজার কথা বলি শোন। একবার আমার এক বন্ধুকে বাইকে বসিয়ে একটা পাহাড়ের রাস্তায় উঠছি।  হঠাৎ দেখি ইঞ্জিন বন্ধ হয়ে বাইক নিচের দিকে নামতে শুরু করেছে। আমিতো ভয় পেয়ে গেছি। কোনোক্রমে দুই বন্ধুর চেষ্টায় বাইক থামিয়ে আবার স্টার্ট দিয়ে উপরে উঠলাম। তুই বল, এখানে বাইক নামার সময় স্থিতঘর্ষণ কোনদিকে কাজ করছিল?

মামা, এটা তো প্যাডেল না করে সাইকেল চালানোর মতোই। যে কেসটার কথা এক্ষুণি বললে। ওজনের ওই উপাংশ  বাইকটাকে নিচে টানার চেষ্টা করবে। আর সেটা আটকাতে স্থিতঘর্ষণ কাজ করবে উপরের দিকে। এই স্থিতঘর্ষণই প্রয়োজনীয় টর্ক দেবে যাতে বাইকের চাকা গড়াতে থাকে নিচের দিকে। এই ঘর্ষণ না থাকলে গড়ানোর বদলে ঘষতে ঘষতে নিচে আসতো বাইকটা।

বাহ! এইজন্য তোকে আমি এত ভালবাসি। সবকিছুই বেশ ভালভাবে শুনিস ও বুঝিস। আজ আপাতত এখানেই থাক। অনেক রাত হয়ে গেল। এবার খেতে চল। কাল তো তোকে আবার বাড়ি রওনা দিতে হবে।

কৃতজ্ঞতা স্বীকার: এই তিনটি পর্বের খসড়া পড়ে ও মতামত দিয়ে লেখাগুলি তৈরী করতে সাহায্য করেছে অনির্বাণ ঘোষ ও অনির্বাণ গঙ্গোপাধ্যায়।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/friction-advantage-disadvantage-part-03

print