চলন্ত অবস্থায় ঘর্ষণ (ঘর্ষণের উৎস - পর্ব ২)

সৌরভ কান্তি দে

(মিরগোদা মৃত্যুঞ্জয় বাণীপীঠ)

 

প্রদীপ্ত পঞ্চাধ্যায়ী

(কাঁথি প্রভাত কুমার কলেজ)

 

22 Oct 2021

Link: https://bigyan.org.in/friction-advantage-disadvantage-part-02

পড়ার ঘরে ঢুকে গতদিনের মতোই মামা তাঁর টেবিলে ক্লাস ইলেভেনের ফিজিক্সের মোটা বইটা আবার রাখলেন। আগের দিন দেখা গেছিলো বইটাকে আস্তে ঠেললে সেটা নড়ে না। এবার মামা বইটাকে আগের দিনের থেকে আর একটু জোর দিয়ে ঠেললেন। তাতেও দেখা গেল বইটা একই জায়গায় থাকলো।

রাহুল বলে উঠলো –

মামা, এবারেও তো সেই আগের মতোই হলো!

ধীরে, বৎস! মামা এবারে বইটাকে আর একটু জোরে ঠেললেন। এবার কিন্তু বইটা সত্যি সত্যি সরে গেল।

মামা এবার একটু বিশদে গিয়ে বোঝানো শুরু করলেন –

মনে কর – প্রথমে আমি ৫০ নিউটন বল দিয়ে ঠেলেছিলাম। কিন্তু বই ছিল স্থির। তার মানে তোর কথামতো বিপরীত দিকেও ৫০ নিউটন ঘর্ষণ বল কাজ করছে। এই ঘর্ষণটা কিন্তু স্থিত ঘর্ষণ (static friction)। কেন বলতো?

টেবিলের উপর বইটা স্থির থাকলো। তাই?

শুধু বইটা স্থির বললে সম্পূর্ণ হয়না। বই ও টেবিলের দুটির স্পর্শতলের মধ্যে কোনো আপেক্ষিক গতি (relative motion) নেই। কিন্তু, আমি যেদিকে ঠেলছি, সেদিকে আপেক্ষিক গতির একটা চেষ্টা বা প্রবণতা রয়েছে। এই আপেক্ষিক গতির প্রবণতার উল্টোদিকে যে ঘর্ষণ বল কাজ করে লব্ধি বলকে (net force) শূন্য করতে সাহায্য করছে সেটিই স্থিত ঘর্ষণ।

আচ্ছা মামা, এক্ষেত্রে স্থিত ঘর্ষণ যে তোমার দেওয়া বলের সমান, এটা নিউটনের তৃতীয় সূত্র দিয়ে ব্যাখ্যা করা যাবে না – তাই তো? কারণ এই দুটি বল একই বস্তুর উপর কাজ করছে।

একদম ঠিক। আবার দেখ, একটু পর বলটা বাড়িয়ে মনে কর ৬০ নিউটন করলাম। তখনো ধর বই স্থির রয়েছে। তার মানে আমার বলের বিপরীতে এখন ৬০ নিউটন স্থিত ঘর্ষণ বল কাজ করছে। তোর কি মনে হয়, যত বল বাড়াতে থাকবো, স্থিত ঘর্ষণ সবসময়েই সেই বলের সমান হবে?

না মামা। যদি তাই হতো, তাহলে কখনোই কোনো বস্তুকে টেনে বা ঠেলে সরাতে পারতাম না। তাতো হয় না।

বাহ! স্থিত ঘর্ষণ একটা নির্দিষ্ট সীমা পর্যন্ত প্রযুক্ত বলের সমান হতে পারে। স্থিত ঘর্ষণের এই সর্বোচ্চ মানটিই আমাদের কাছে সীমাস্থ ঘর্ষণ (limiting friction) নামে পরিচিত। যখন প্রযুক্ত বলের মান সীমাস্থ ঘর্ষণকে ছাপিয়ে যায়, তখন দুটির স্পর্শতলের মধ্যে আপেক্ষিক গতির সৃষ্টি হয়। এই আপেক্ষিক গতির বিপরীতেও কিন্তু ঘর্ষণবল কাজ করে। একে বলে চলঘর্ষণ (kinetic friction)।

চলঘর্ষণ কিন্তু সীমাস্থ ঘর্ষণের চেয়ে সামান্য কম হয়। এটাও হয়তো তুই জানিস। তাই আমার দেওয়া বলটা যখন সীমাস্থ ঘর্ষণকে ছাপিয়ে বইটাকে সরাতে শুরু করলো, সেটা বই চলাকালীন চলঘর্ষণের থেকেও বেড়েই রইলো। তাই বইটাও চালু রইলো।

যদি ঘর্ষণকে নিউটনের তৃতীয় সূত্র দিয়ে ব্যাখ্যা করতে যেতাম, তাহলে এই চলঘর্ষণের ক্ষেত্রেই ভুলটা ধরা পড়তো। স্থিত ঘর্ষণ নাহয় আমার দেওয়া বল অনুসারে বাড়ছিল। যত বল বাড়াচ্ছিলাম, একটা সীমা অব্দি ঘর্ষণের মানও ততটাই হচ্ছিলো। কিন্তু দুটি নির্দিষ্ট তলের মধ্যে চলঘর্ষণের মান ধ্রুবক। যতই আমার বল বাড়াই, উল্টোদিকে ঘর্ষণ একই থাকবে। যদি চলঘর্ষণের মান প্রযুক্ত বল -এর কম হয়, তখন বইটা প্রযুক্ত বলের দিকে ত্বরণসহ গতিশীল হবে (accelerated motion)। আর বেশি হলে বইয়ের বেগ ক্রমশ কমতে থাকবে এবং একটা সময় থেমে যাবে। এরপর আবার বইটাকে চালু করতে হলে আমার বলকে সীমাস্থ ঘর্ষণের থেকে বেশি হতে হবে। আর যদি বই গতিশীল হওয়ার পর হয়, তাহলে বই সমবেগ নিয়ে চলতে থাকবে। বলের কথা ভাবতে গেলে অনেকেই আমরা যে ভুলটা করি, তা হল – বল বস্তুর গতির সাথে সম্পর্কিত। কিন্তু এই ভাবনাটি সম্পূর্ণ সঠিক নয়। আসলে বলের সংজ্ঞানুযায়ী, লব্ধি বলের মান শূন্য না হলে অর্থাৎ অপ্রতিমিত বল (unbalanced force) থাকলে বস্তুতে ত্বরণ সৃষ্টি হয়।

অবশ্য ঘর্ষণ যে নিউটনের তৃতীয় সূত্র অনুযায়ী আমার বলের প্রতিক্রিয়া নয়, সেটা আমরা আগেই দেখেছি। ঘর্ষণবলের উৎস আলাদা। এখানে আর একটা কথা বলে রাখি, অন্যান্য সকল বলের মতো ঘর্ষণবল কিন্তু জোড়ায় থাকে। এটা কিন্তু নিউটনের তৃতীয় সূত্রের জন্য। যেমন ধর টেবিল বইয়ের উপর যে পরিমাণ ঘর্ষণ বল দিচ্ছে, বইও টেবিলের উপর সমপরিমাণে ও বিপরীত দিকে ঘর্ষণ দিচ্ছে। এই দুটো ঘর্ষণ দুটো আলাদা আলাদা বস্তুর আপেক্ষিক গতিকে বাধা দেয়, এক্ষেত্রে বই আর টেবিল।

আগেই বলেছি, বস্তুর উপর প্রযুক্ত লম্ব প্রতিক্রিয়া বল যত বেশি হয় বস্তু দুটির স্পর্শতলের অণুগুলি তত পরস্পরের কাছাকাছি আসে। ফলে আণবিক বল বেশি হওয়ায় সীমাস্থ ঘর্ষণ ও চল ঘর্ষণ এর মান বেড়ে যায়। এই লম্ব প্রতিক্রিয়ার সাথে বাড়া কমাকে একটা সমীকরণ দিয়ে লেখা হয়:

সীমাস্থ ঘর্ষণ = স্থিতঘর্ষণ গুণাঙ্ক x লম্ব প্রতিক্রিয়া

চলঘর্ষণ = চলঘর্ষণ গুণাঙ্ক x লম্ব প্রতিক্রিয়া

ঘর্ষণ গুণাঙ্কের (coefficient of friction) মান স্পর্শ তলের প্রকৃতির উপর নির্ভর করে। বস্তু একবার গতিশীল হতে শুরু করলে তখন ঘর্ষণজনিত বাধা একটু কমে যায়। তাই চল ঘর্ষণ গুণাঙ্কের মান স্থিত ঘর্ষণ গুণাঙ্কের চেয়ে একটু কম হয়।

ঠিক যেমন কোনো কাজ শুরু করবার আগে আমাদের অনেক বাধা পেরোতে হয়। আর একবার কাজের মধ্যে ঢুকে গেলে অনেকটা সহজে কাজে এগোনো যায়।

ভালোই বলেছিস। তবে আসল ব্যাপারটি হল – দুটি স্পর্শতলের মধ্যে আপেক্ষিক গতি না থাকলে প্রকৃত স্পর্শ অঞ্চলগুলিতে কতকগুলো শক্তিশালী আণবিক বন্ধনীর সৃষ্টি হয়। এই বন্ধনীগুলোই স্থিত ঘর্ষণের উৎস। এই শক্তিশালী আণবিক বন্ধনের জন্যই বল প্রয়োগ করা সত্ত্বেও দুটি স্পর্শতলের আপেক্ষিক গতি শুরু হয়ে যায় না। বরং ঐ বলের মান একটি সীমা (সীমাস্থ ঘর্ষণ) না পেরোলে আপেক্ষিক গতি শুরু হয় না। বস্তুকে গতিশীল করতে হলে দুটি স্পর্শতলের মধ্যে এই আণবিক বন্ধনকে ভাঙতে হয়, অর্থাৎ প্রযুক্ত বলকে সীমাস্থ ঘর্ষণ অপেক্ষা বেশি হতে হয়। প্রযুক্ত বল সীমাস্থ ঘর্ষণ অপেক্ষা বেশি হলে বস্তু চলতে শুরু করে, তখন এই আণবিক বন্ধন গুলি ভাঙতে থাকে এবং নতুন নতুন আণবিক বন্ধনের উৎপত্তি ঘটে অর্থাৎ, চল ঘর্ষণ সৃষ্টি হয়। কিন্তু বস্তুর অণুগুলির গতিশীলতার জন্য এই আণবিক বন্ধনগুলি স্থির অবস্থার আণবিক বন্ধনের মতো শক্তিশালী হওয়ার সময় পায় না। তাই সীমাস্থ ঘর্ষণ অপেক্ষা চল ঘর্ষণের মান কম হয়।মামা এবার বইটিকে টেবিলের উপর রেখে টেবিলটিকে ঠেলতে শুরু করলেন।

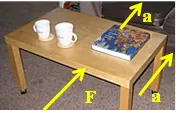
দেখা গেল, টেবিল ও বই একসাথে গতিশীল অর্থাৎ গতিশীল টেবিলের সাপেক্ষে বই স্থির।

আমি তো টেবিলকে ঠেললাম, বইতে হাত দিইনি। তবে বইকে টেবিলের সাথে সাথে কে নিয়ে গেল?

দেখ, এখানেও বই ও টেবিলের মধ্যে আপেক্ষিক গতি নেই। কিন্তু আমি টেবিলে বল প্রয়োগ করে বইয়ের সাপেক্ষে টেবিলকে সামনে নিয়ে যেতে চাইছি। অর্থাৎ, বইয়ের সাপেক্ষে টেবিলের একটা আপেক্ষিক গতির প্রবণতা রয়েছে। সুতরাং, বলা যেতে পারে, টেবিলের সাপেক্ষে বইয়েরও পেছনের দিকে আপেক্ষিক গতির প্রবণতা রয়েছে। তাই এই আপেক্ষিক গতির প্রবণতার বিপরীতে স্থিত ঘর্ষণ কাজ করবে, যা বইকে টেবিলের সাথে সাথে নিয়ে যাবে (চিত্র ২)।

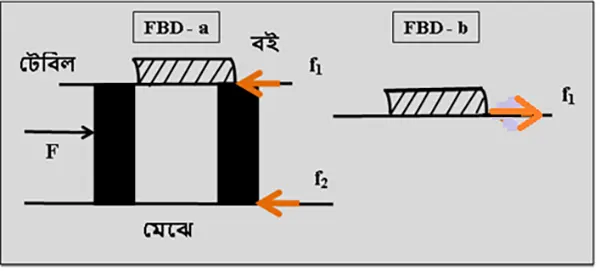
একটা ইন্টারেস্টিং ব্যাপার দেখ – এখানে কিন্তু স্থিতঘর্ষণই বইকে গতিশীল হতে সাহায্য করছে। তাই “স্থির থাকলেই যে স্থিত ঘর্ষণ কাজ করবে” – এই নিয়মটা আর যে ঠিক নয়, তা পরিষ্কার বোঝা গেলো। হ্যাঁ, বলতে পারিস – আপেক্ষিক গতি না থাকলেও শুধু তার প্রবণতা থাকলেই স্থিত ঘর্ষণ ক্রিয়াশীল হয়। আর একটা ব্যাপারে আমাদের মাথায় ভুল ধারণা গেঁথে যায়, তা হলো – ঘর্ষণ গতির বিপরীতে কাজ করে। এটা একদমই ভুল ধারণা। তুইতো এখানে দেখলি, স্থিত ঘর্ষণই বইটাকে টেবিলের গতির অভিমুখে নিয়ে যাচ্ছে। সঠিক কথাটি হলো – ঘর্ষণ আপেক্ষিক গতি বা আপেক্ষিক গতির প্রবণতার বিপরীতে ক্রিয়াশীল হয়। একটা free body diagram (FBD) এর (চিত্র ৩) মাধ্যমে ব্যাপারটা দেখাই –

(টেবিলের ক্ষেত্রে ভর = , ত্বরণ = )

(বইয়ের ক্ষেত্রে ভর = , ত্বরণ = )

খুব ইন্টারেস্টিং ব্যাপার তো!!

হুম, আরো মজা আছে। এবার তুই বল, স্থির টেবিলের উপর এই বইটাকে ত্বরণে (চিত্র ৪) ঠেলে নিয়ে যেতে হলে কত বল প্রয়োগ করতে হবে? মনে কর, চলঘর্ষণ বল ।

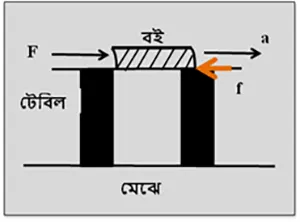
রাহুল করে দেখালো –

বা,

দারুন ভাগ্নে!! এবার মনে কর, স্থির টেবিলের উপর বইটাকে v সমবেগে নিয়ে যাওয়ার সময় কী হবে?

এক্ষেত্রে বইতে প্রযুক্ত বল () = চলঘর্ষণ ()। অর্থাৎ, বইতে নীট বল শুন্য। তাই বই সমবেগে গতিশীল।

ঠিক ধরেছিস। এখন খেয়াল কর, বইয়ের উপর এই এক টাকার কয়েনটি রাখলাম। আমি যদি বইটির একটি প্রান্তকে আনত তলের মতো করে একটু তুলি, সেক্ষেত্রে কি কয়েনটি পড়ে যাচ্ছে?

না মামা। কিন্তু আর একটু তুললে কয়েনটি পিছলে পড়ে যাবে।

আমাকে বলতে পারবি কেন এমন হবে?

রাহুল একটু ভেবে বললো:

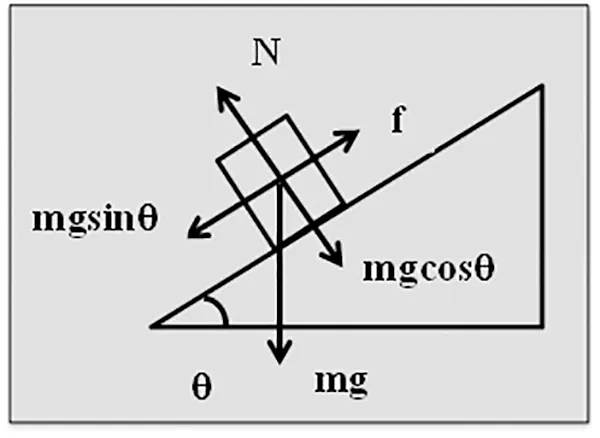
মামা, এক্ষেত্রে কিন্তু কয়েনের ওজনের দুটি উপাংশ নিতে হবে (চিত্র ৫)। যদি কয়েনের ওজনের মান mg ধরি, তাহলে উপাংশ  কয়েনকে বই এর  নততল বরাবর পিছলে যেতে সাহায্য করবে। অন্য দিকে লম্ব প্রতিক্রিয়া উপাংশের সমান হবে। সুতরাং বই ও কয়েনের মধ্যে সীমাস্থ ঘর্ষণের মান , যেখানে হলো স্থিতঘর্ষণ গুণাঙ্ক। যখন সীমাস্থ ঘর্ষণ ()-এর মানের থেকে -এর মান কম হয়, তখন কয়েনের উপর -এর উল্টোদিকে যে স্থিত ঘর্ষণ কাজ করে তা -এর সমান হয়। ফলে নততল বরাবর লব্ধি বল শূন্য হওয়ায় কয়েন আগের মতো স্থির থাকে। -র মান বাড়লে -র মান বাড়ে এবং -র মান কমে। ফলে ক্রমশ কয়েনের উপর বাড়ে এবং সীমাস্থ ঘর্ষণ কমে। একসময় সীমাস্থ ঘর্ষণের সমান হয়, তখনও কয়েন স্থির থাকে। যখন -র মান সীমাস্থ ঘর্ষণের থেকে বেশি হয়, তখন কয়েন বইয়ের নততল বরাবর নিচের দিকে নামতে থাকে। এই অবস্থায় নততল বরাবর উপরের দিকে চলঘর্ষণ ক্রিয়া করে, যার মান সীমাস্থ ঘর্ষণের থেকে একটু কম হয়।

বেশ। এবং দেখ চলঘর্ষণও কিন্তু লম্ব প্রতিক্রিয়া () আর চলঘর্ষণ গুণাঙ্কের গুণফলের সমান। সুতরাং, বুঝতেই পারছিস, স্থিত ঘর্ষণ গুণাঙ্কের থেকে চলঘর্ষণ গুণাঙ্কের মান একটু কম হয়।

এবার মনে কর, এই বইটাকে যদি আমি একটা নততল বরাবর উপরের দিকে স্থির ত্বরণে নিয়ে যাই, তখন কী ঘটবে?

মামা বলতে থাকলেন –

ব্যাপারটা একটু ধাপে ধাপে বোঝ। আচ্ছা দেখ, বইয়ের ওজনের একটি উপাংশ যা কিন্তু নততল বরাবর নিচের দিকে কাজ করছে। আর আমি বল প্রয়োগ করছি নততল বরাবর উপরের দিকে। তাহলে উপরের দিকে লব্ধি বল () যখন সীমাস্থ ঘর্ষণের মানের থেকে বেশি হবে, তখন বইটি বলের দিকে গতিশীল হবে। এখানে খেয়াল করে দেখ, আগের মতো ঘর্ষণ বল কিন্তু নততল বরাবর উপরের দিকে কাজ করছে না। বরং নততল এর সাপেক্ষে বই উপরের দিকে চলতে শুরু করলেই তার বিপরীতে দিকে কাজ করবে চলঘর্ষণ । চলঘর্ষণ থেকে যখন () বেশি হবে, তখন বইটি নততলের উপরের দিকে চলতে শুরু করবে একটি ত্বরণ নিয়ে। আর যখন এই নীট বল () চলঘর্ষণের সমান হবে, বই একটি নির্দিষ্ট বেগ নিয়ে নততলের উপরের দিকে উঠবে। সেক্ষেত্রে (চিত্র ৬) দেখ,

– চলঘর্ষণ = (প্রথম ক্ষেত্রে)

– চলঘর্ষণ = (দ্বিতীয় ক্ষেত্রে)

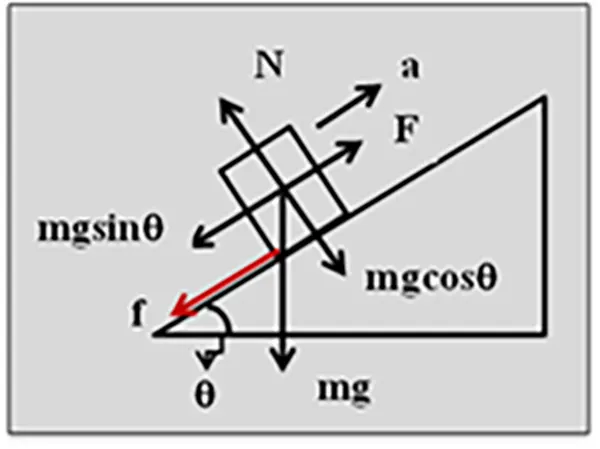
মামা! দারুন ব্যাপার তো।

হুম! ঘর্ষণ ব্যাপারটা খুবই ইন্টারেস্টিং। তোকে আরো কিছু ক্ষেত্রে দেখাই, সেখানে ঘর্ষণ কি ভূমিকা নিচ্ছে! কিন্তু আজ আর না, রাতের খাবার সময় হয়ে গিয়েছে। কাল আমরা চাকার ঘর্ষণের ব্যাপারে কথা বলবো।

(চলবে)

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/friction-advantage-disadvantage-part-02

print