21-11-2024 09:26:58 am

print

 

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

 

শক্তি ও ভরবেগ সংরক্ষণ — এক আপাত দ্বন্দ্ব

%e0%a6%b8%e0%a7%8c%e0%a6%b0%e0%a6%ad-%e0%a6%95%e0%a6%be%e0%a6%a8%e0%a7%8d%e0%a6%a4%e0%a6%bf-%e0%a6%a6%e0%a7%87
সৌরভ কান্তি দে

(মিরগোদা মৃত্যুঞ্জয় বাণীপীঠ)

 
%e0%a6%aa%e0%a7%8d%e0%a6%b0%e0%a6%a6%e0%a7%80%e0%a6%aa%e0%a7%8d%e0%a6%a4-%e0%a6%aa%e0%a6%9e%e0%a7%8d%e0%a6%9a%e0%a6%be%e0%a6%a7%e0%a7%8d%e0%a6%af%e0%a6%be%e0%a7%9f%e0%a7%80
প্রদীপ্ত পঞ্চাধ্যায়ী

(কাঁথি প্রভাত কুমার কলেজ)

 
%e0%a6%b8%e0%a7%8c%e0%a6%ae%e0%a7%87%e0%a6%a8-%e0%a6%b8%e0%a6%b0%e0%a6%95%e0%a6%be%e0%a6%b0
সৌমেন সরকার

(কড়ুই পি.সি. হাই স্কুল)

 
%e0%a6%b8%e0%a6%9e%e0%a7%8d%e0%a6%9c%e0%a7%9f-%e0%a6%95%e0%a7%81%e0%a6%ae%e0%a6%be%e0%a6%b0-%e0%a6%aa%e0%a6%be%e0%a6%b2
সঞ্জয় কুমার পাল

(আনন্দপুর উচ্চ মাধ্যমিক বিদ্যালয়)

 
21 Sep 2023
 

Link: https://bigyan.org.in/energy-momentum-conservation

%e0%a6%b6%e0%a6%95%e0%a7%8d%e0%a6%a4%e0%a6%bf-%e0%a6%93-%e0%a6%ad%e0%a6%b0%e0%a6%ac%e0%a7%87%e0%a6%97-%e0%a6%b8%e0%a6%82%e0%a6%b0%e0%a6%95%e0%a7%8d%e0%a6%b7%e0%a6%a3-%e2%80%94-%e0%a6%8f%e0%a6%95

ঘর্ষণ বা friction-এর ফলে তাপ সৃষ্টি হয়। তাই সাধারণ বুদ্ধি আর ফিজিক্স পাঠ্যবই বলে যে, কোনো বস্তুর ওপর ঘর্ষণ থাকলে তার চলার সময় ঘর্ষণের বিরুদ্ধে কাজ করার ফলে যান্ত্রিক শক্তি কিছুটা ক্ষয় হয়। তাই সেসব ক্ষেত্রে শক্তি সংরক্ষণ সূত্র প্রয়োগ করে যেকোনো দুটো সময়ের শক্তিকে সমান ভাবলে অঙ্ক ঘেঁটে যেতে পারে। কিন্তু একটা বিশেষ ক্ষেত্রে ঘর্ষণ থাকা সত্ত্বেও শক্তি সংরক্ষণ সূত্র কাজ করে। সেটা হলো বিশুদ্ধ গড়ানোর ক্ষেত্রে - যখন একটা বস্তু শুধুই গড়াচ্ছে, জমির সাপেক্ষে একটুও পিছলে যাচ্ছে না। কেন এই বিশেষ ক্ষেত্রে ঘর্ষণ সত্ত্বেও শক্তি সংরক্ষণ সূত্র ব্যবহার করা যায়? সেটা বুঝতে হলে একটু অঙ্ক করতে হবে। বাস্তবে, নততলের উপর দিয়ে একটি গোলক ও একটি নিরেট চোঙ (ড্রাম) গড়িয়ে তাদের গতি পরীক্ষা করেও দেখা যাক কি ঘটে ! দেখা যাক, অঙ্কের সাথে বাস্তবের ফলাফল মেলে কিনা?

ছোটবেলায় ভৌতবিজ্ঞান পড়ার সময় শক্তির ধারণা কেমন হয়েছিল মনে করার চেষ্টা করছিলাম।

প্রথমেই মনে এল টিভিতে ‘শক্তিমান’ ধারাবাহিকের কথা কিংবা নারায়ণ দেবনাথের তৈরি চরিত্র ‘বাটুল দি গ্রেট’ -এর কথা। আর তার সাথে নিখিলদার ব্যাখ্যা। নিখিলদা কিছুটা শরৎচন্দ্রের মেজদার মতো। খেলার পরে আড্ডায় একদিন শক্তির তত্ত্ব বোঝাতে গিয়ে বললো : “বাঁটুল দেখ কত কিছু করতে পারে। বাঁটুল যখন স্থির হয়ে দাঁড়িয়ে থাকে, কত শক্তি তার মধ্যে জমা থাকে। সব তখন স্থিতিশক্তি (potential energy)। ছিঁচকে দুটো গোলমাল করলে বা লোকজনকে বিপদ থেকে উদ্ধার করতে বাঁটুল হঠাৎ ছুটে গিয়ে কত বড় বড় পাথর তুলে ছোঁড়ে। তখনই স্থিতিশক্তি খরচা হয়ে তৈরি হয় গতির জন্য শক্তি (kinetic energy)। তারপরে বড় হওয়ার সাথে সাথে বইতে পড়লাম ঢিল ছোঁড়ার উদাহরণ। এর বিজ্ঞান অবশ্য প্রায় সকলের জানা।”

ঢিল উপরে ওঠার পথে শক্তি সংরক্ষণ

ঢিলকে মাটি থেকে একেবারে খাড়াভাবে উপরের দিকে ছুঁড়ে দিলে ঢিল যত উপরের দিকে ওঠে, আমরা দেখতে পাই তার দ্রুতি (speed) আস্তে আস্তে কমে যাচ্ছে এবং এক জায়গায় গিয়ে শূন্য হয়ে গেল। দ্রুতি কমার অর্থ, তার গতিশক্তি কমতে থাকছে। ফলস্বরূপ ঢিলের মধ্যে স্থিতিশক্তির পরিমাণ বাড়তে থাকছে।

যে মুহূর্তে ঢিলটি সবচেয়ে বেশি উচ্চতায় ওঠে, সেই সময় তার গতিশক্তি শূন্য হয় এবং স্থিতিশক্তি সবচেয়ে বেশি হয়।

আবার ঐ সর্বোচ্চ বিন্দু থেকে নিচে নামার সময় ঠিক উল্টো ঘটনা ঘটে। অভিকর্ষ বলের দিকে ঢিলটি নেমে আসে বলে তার দ্রুতি বাড়তে থাকে। ফলে বস্তুর গতিশক্তি বাড়তে থাকে এবং স্থিতিশক্তি কমতে থাকে। নামতে নামতে একেবারে মাটিতে ঠেকে যাওয়ার সময় বস্তুর গতিশক্তি সর্বোচ্চ এবং মাটির তলের সাপেক্ষে বস্তুর স্থিতিশক্তি শূন্য হয়। আর সহজ অঙ্ক দিয়ে তো দেখাই যায় যে, ওঠার সময় কিংবা নামার সময় যে কোনো বিন্দুতে এই গতিশক্তি ও স্থিতিশক্তি যোগ করলে যোগফল সব সময় স্থির থাকে।

আবার এও দেখানো যায় যে কোনো নির্দিষ্ট উচ্চতায় ঢিলের দ্রুতি একই থাকে, সে ওঠার সময়ই হোক বা নামার সময়। এই ঘটনায় মোট শক্তির মান হিসেব করার ক্ষেত্রে বায়ুর বাধা অগ্রাহ্য করা হয়। অর্থাৎ শুধুমাত্র অভিকর্ষীয় বল উপস্থিত থাকলে যান্ত্রিক শক্তি (গতিশক্তি ও স্থিতিশক্তির যোগফল) সংরক্ষিত হওয়ার ব্যাপারটা বোঝা যায়। তাই অভিকর্ষীয় বা মহাকর্ষ বলকে আমরা সংরক্ষী বল বলি (conservative force)।

ওঠার সময় কিংবা নামার সময় যে কোন বিন্দুতে গতিশক্তি ও স্থিতিশক্তির যোগফল স্থির থাকে।




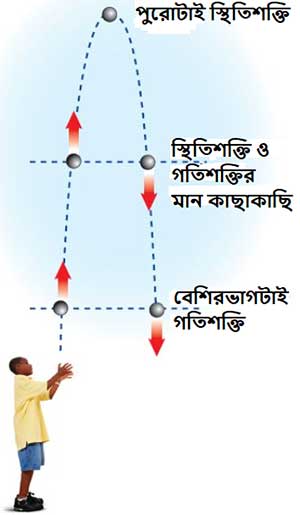
ঢিলের যে কোনো অবস্থানে মোট যান্ত্রিক শক্তির পরিমাণ ধ্রুবক (ছবির সূত্র)

শক্তির সংরক্ষণ কি সর্বত্র প্রযোজ্য?

এই ঢিল ছোঁড়ার ঘটনায় বায়ুর বাধা নগণ্য না হলে বস্তুর উপরে ওঠা বা নীচে নামার সময় বায়ুর সাথে ঘর্ষণের জন্য কিছু শক্তি নষ্ট হয়।

তখন যত সময় গড়ায় ততই গতিশক্তি ও স্থিতিশক্তির যোগফল কমতে থাকে। ঘর্ষণের বিরুদ্ধে যে কাজ করা হয় তা মূলত তাপশক্তির আকারে নষ্ট হয়ে যায়। তাই যান্ত্রিক শক্তি ক্রমশ কমে যায়। সে কারণে ঘর্ষণকে অসংরক্ষী বল (dissipative force) বলে।

ঘর্ষণকে উপেক্ষা করলে বস্তু ভূপৃষ্ঠ থেকে উপরে উঠে আবার ভূপৃষ্ঠে ফিরে এলে মোট কৃতকার্য (work done) শূন্য হয়। অর্থাৎ উপরে ওঠার সময় অভিকর্ষ বলের বিরুদ্ধে যে কার্য হয়, নীচে নামার সময় অভিকর্ষ বলের দ্বারা সেই একই পরিমাণ কাজ করা হয়। সুতরাং বলা যায় সংরক্ষী বলের ক্ষেত্রে যে কোন নির্দিষ্ট ঘেরা পথে মোট কৃতকার্য শূন্য হয়।

কিন্তু অমসৃণ মেঝেতে একটা বস্তুকে ঠেলে কিছুটা নিয়ে গেলে আবার সেখান থেকে প্রথম অবস্থানে টেনে নিয়ে এলে, সরণ শূন্য হলেও কৃতকার্য শূন্য হয় না। কারণ, বস্তুর যাওয়ার সময় চলঘর্ষণের বিরুদ্ধে যেমন কাজ করতে হয়, তেমনই ফিরে আসার সময়ও চলঘর্ষণের বিরুদ্ধে কাজ হয়। তাই বলা চলে, অসংরক্ষী বলের ক্ষেত্রে কোনো বদ্ধ পথে মোট কার্য কিন্তু শূন্য হয় না।

বিভিন্ন বাস্তব সমস্যার ক্ষেত্রে করা কাজের সঠিক হিসেব পাওয়ার জন্য গতিশক্তি ও স্থিতিশক্তির সাথে সাথে ঘর্ষণের বিরুদ্ধে কাজকেও খেয়াল রাখতে হয়। অধিকাংশ ক্ষেত্রেই ঘর্ষণ বলের প্রভাব থাকে, সেটা যত কমই হোক না কেন। সেই সব জায়গায় যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা যায় না। বলা ভালো, প্রায় সব বাস্তব ক্ষেত্রেই যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা যায় না। শুধুমাত্র যেখানে ঘর্ষণকে উপেক্ষা করা সম্ভব হয় সেখানে এই সূত্র প্রয়োগ করা যায়।

প্রায় সব বাস্তব ক্ষেত্রেই ঘর্ষণের কারণে যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা যায় না।

খুব সঙ্গত ভাবেই একটি প্রশ্ন মনের কোনে উঁকি দেয়: ঘর্ষণ থাকলে কি কোনোভাবেই যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা যাবে না?

কখনো সখনো যেতে পারে। যেমন, শুধুমাত্র গড়িয়ে যাওয়া বস্তুর ক্ষেত্রে যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা যায়। ঘর্ষণ থাকলেও যেতে পারে। এরকমটা কেন?

কেন সেটা বুঝতে একটি প্রতিদিনের পরিচিত ছবির কথা ভাবা যাক। বাজারে গেলে কেরোসিন দোকানের সামনে একটা দৃশ্য সাধারণত চোখে পড়ে। ট্রাক থেকে কেরোসিন ড্রাম নামছে। সেক্ষেত্রে একটি নততল ব্যবহার করা হয়, আর বহুল ব্যবহারের ফলে নততলটি ক্রমশ অমসৃণ হতে থাকে। ধরো, একটি তেলভর্তি ড্রাম এমন একটি অমসৃণ নততলের (মাটির সাথে \theta কোণ করে লাগানো) কোনো একটি অবস্থান থেকে স্থির অবস্থা থেকে গড়িয়ে গড়িয়ে নিচে নামতে থাকলো। এভাবে একটি নির্দিষ্ট দূরত্ব নামার পর বস্তুর ত্বরণ কত হবে?

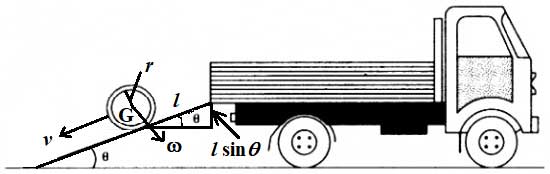
নততলে গড়িয়ে নামা ড্রামের ক্ষেত্রে স্থিতিশক্তির গতিশক্তিতে রূপান্তর।

শক্তির সংরক্ষণ সূত্র ধরে নিয়ে অঙ্ক কষা

চলো, এর উত্তর আমরা ধাপে ধাপে খুঁজে দেখি।

প্রথমেই আসি যান্ত্রিক শক্তি সংরক্ষণের প্রসঙ্গে।  সহজে বোঝার জন্য অঙ্ক করার সময় আমরা ধরে নেবো বস্তু এবং ব্যবহৃত নততল বেশ দৃঢ়, যেখানে দৃঢ়তার দিক দিয়ে আদর্শ বলে গণ্য করতে পারি। ফলে এখানে আবর্ত  ঘর্ষণের ব্যাপারটা আমাদের অঙ্কে আসবে না।     

একটি নির্দিষ্ট দূরত্ব (l) নামার পর ধরো m ভরের ড্রামটির ভরকেন্দ্রের রৈখিক দ্রুতি (linear speed) হলো v এবং কৌণিক দ্রুতি (angular speed) হলো \omega। এই অবস্থায় ড্রামটির মোট গতিশক্তি:

\frac{1}{2}mv^2 + \frac{1}{2}I\omega^2

এখানে I হলো ঘূর্ণাক্ষের (center of rotation) সাপেক্ষে ড্রামটির জড়তা ভ্রামক (moment of inertia)। কিন্তু শুরুতে ড্রামটির কোনো গতি ছিল না। তাহলে সেটা গতিশক্তি কোত্থেকে পেলো?

যান্ত্রিক শক্তি সংরক্ষণ সূত্রের ধারণা প্রয়োগ করে বলা যায়, ড্রামটি নততল বরাবর l দূরত্ব গড়িয়ে নিচে নামার জন্য কিছুটা স্থিতিশক্তি হারায়। স্থিতিশক্তি হারিয়ে শক্তিটা গতিশক্তি হিসেবে লাভ করে। অর্থাৎ, স্থিতিশক্তির হ্রাস = গতিশক্তির বৃদ্ধি । অঙ্কের ভাষায় বললে,

mgl\sin\theta = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2

= \frac{1}{2}mv^2 + \frac{1}{2} \times \frac{1}{2}mr^2 \times (\frac{v}{r})^2

= \frac{1}{2}mv^2 + \frac{1}{4}mv^2

= \frac{3}{4}mv^2

এখানে, ড্রামটি নততলে l দূরত্ব নামার জন্য উল্লম্ব অভিমুখে (perpendicular direction) l\sin\theta দূরত্ব নামে। তাই অভিকর্ষ স্থিতিশক্তির হ্রাস mgl\sin\theta। এখানে আরেকটা জিনিস ব্যবহার করা হয়েছে: বিশুদ্ধ গড়ানো বস্তুর ক্ষেত্রে v = \omega r হয়। উপরের অঙ্কটি আর একটু কষলে লেখা যাবে:

v^2 = \frac{4}{3}gl\sin\theta

এবার ধরা যাক, নততল বরাবর ড্রামটি a ত্বরণে নামে। গতির সমীকরণ থেকে লেখা যায় —

v^2 = u^2 + 2al = 0 + 2al = 2al

যদি ড্রামের প্রাথমিক বেগ u = 0 হয়।

উপরের দুটি সমীকরণ থেকে বলা যায় —

a = \frac{2}{3}g \sin\theta

কিন্তু শুধুমাত্র গড়ানো গতির ক্ষেত্রেও স্পর্শতলে কিন্তু স্থিতঘর্ষণ রয়েছে। তাহলে উপরের অঙ্কটিতে যান্ত্রিক শক্তির সংরক্ষণ সূত্র  প্রয়োগ করা কি ঠিক হলো?

গড়ানো গতির ক্ষেত্রেও স্থিতঘর্ষণ রয়েছে, তাহলে শক্তি সংরক্ষণ প্রয়োগ করা কি ঠিক হলো?

শক্তির সংরক্ষণ না ধরে অঙ্ক কষা

আমরা এখন অন্য ধারণা থেকে ড্রামটির ত্বরণ বের করবো। যদি এই ধারণা থেকে ত্বরণের প্রাপ্ত মান প্রথমটির সাথে পুরোপুরি মিলে যায় তবেই বলবো এই সমস্যায় যান্ত্রিক শক্তির সংরক্ষণ সূত্রের প্রয়োগ করে আমরা ঠিক করেছি। চলো দেখা যাক। আমরা অন্যভাবে ড্রামের ত্বরণ বের করতে লেগে পড়ি।

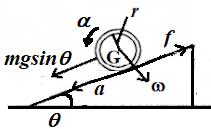
নততলে গড়িয়ে নামা ড্রামের ক্ষেত্রে বিভিন্ন ক্রিয়াশীল বলের ভূমিকা

ছবিটাকে লক্ষ করো।

নিউটনের দ্বিতীয় সূত্র থেকে বলা যায়,

mg \sin\theta - f = ma

 f এখানে স্থিতঘর্ষণ এবং a হলো ড্রামের ত্বরণ।

ড্রাম যত নিচের দিকে নামতে থাকে, ততই তার কৌণিক বেগ (angular velocity) বাড়তে থাকে, অর্থাৎ তৈরি হয় এক কৌণিক ত্বরণ (angular acceleration)। ভরকেন্দ্রগামী অক্ষের (axis) সাপেক্ষে স্থিতঘর্ষণের জন্য তৈরি হওয়া টর্কের (torque) জন্য ড্রামে কৌণিক ত্বরণের সৃষ্টি হয়। তাই কৌণিক ত্বরণ যদি \alpha হয়,এই ধারণা থেকে বলা যায়:

fr = I\alpha

বিশুদ্ধ গড়ানো গতির ক্ষেত্রে a = \alpha r হয়। তাই:

f = I\frac{a}{r^2} = \frac{1}{2}mr^2 \times \frac{a}{r^2} = \frac{ma}{2}

স্থিতঘর্ষণ বল f-এর এই মানটি উপরের বলের সমীকরণে বসালে:

ma + \frac{ma}{2} = mg \sin\theta

অতএব,

a = \frac{2}{3}g \sin\theta

আরে, ত্বরণের এই মানটিই তো সংরক্ষণ সূত্রের ধারণা থেকেও পাওয়া গিয়েছিল!!!

ঘর্ষণ সত্ত্বেও গড়ানোর সময় শক্তি সংরক্ষণ লাগানো যায় কি?

এই হিসেব প্রমাণ করে, নততলে বিশুদ্ধ গড়ানো গতির ক্ষেত্রে যান্ত্রিক শক্তি (mechanical energy) সংরক্ষিত হয়। মাথায় রাখতে হবে ড্রাম ও নততলের স্পর্শ বিন্দুতে ঘর্ষণ কাজ করে, যদিও বা সেটি স্থিত ঘর্ষণ। তাহলে কি স্থিত ঘর্ষণ উপস্থিত থাকলেও যান্ত্রিক শক্তির সংরক্ষণ সূত্র বিঘ্নিত হয় না (আগে যা বললাম তার উল্টো)? এখনো সিদ্ধান্ত নেওয়ার সময় হয়নি।

এই ফাঁকে আমরা আর একটি ঘটনার উপর আলোকপাত করবো। এখানে চলঘর্ষণ (kinetic friction) ক্রিয়াশীল।

ধরা যাক একটি r ব্যাসার্ধের, m ভরের লোহার বল (নিরেট গোলক) একটি অনুভূমিক মেঝের উপর স্থিরভাবে রাখা আছে। আলোচনার সুবিধার জন্য বলটিকে (ball) গোলক হিসেবে উল্লেখ করবো, নইলে অন্য বলের (force) সাথে গুলিয়ে যেতে পারে। এবার গোলকটিতে তার কেন্দ্রগামী একটা অনুভূমিক রেখা বরাবর মেঝের সমান্তরালে একটা ঘাত দেওয়া হলো। এর ফলে গোলকটি, মনে করো, প্রথমে V রৈখিক দ্রুতি (linear speed) নিয়ে মেঝের উপর পিছলে চলতে শুরু করলো। একটা সময় পরে দেখা গেল গোলকটি না পিছলে গড়িয়ে চলতে শুরু করেছে। এই অবস্থায় গোলকের কেন্দ্রের দ্রুতির একটা হিসেব বের করবো ।

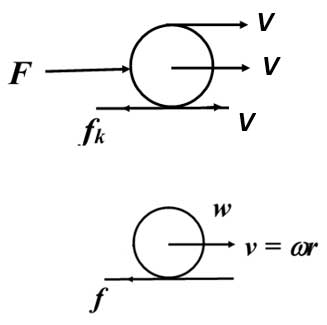
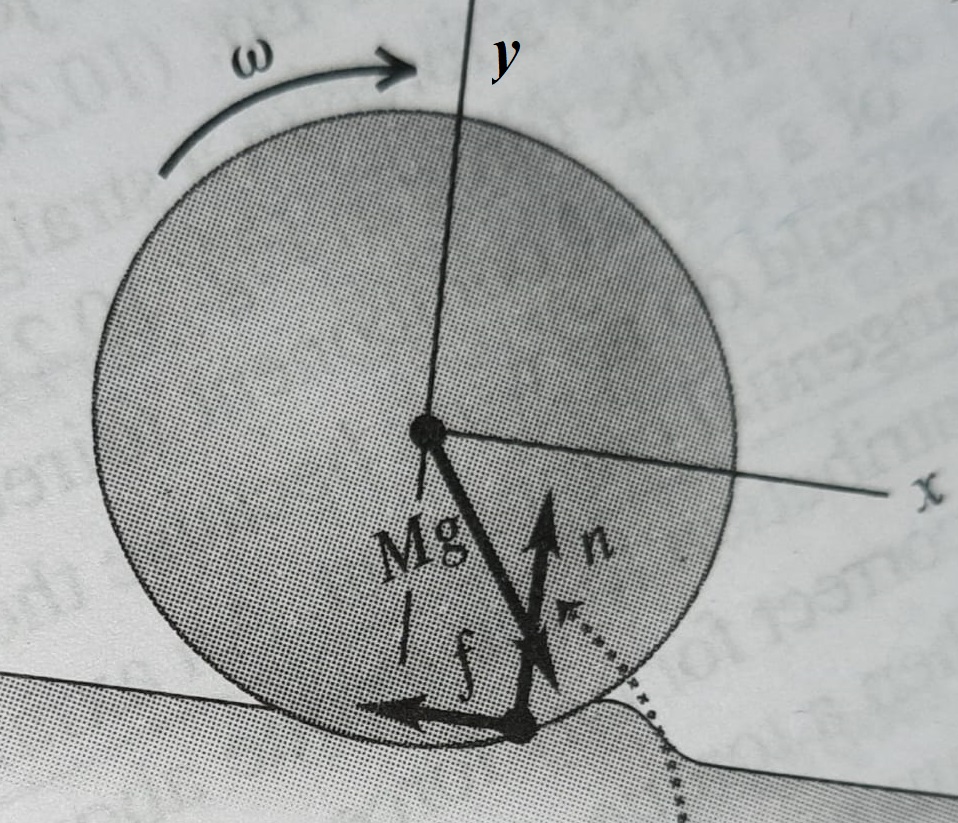
উপরের ছবি : প্রারম্ভিক মুহূর্তে (t = 0) কেবলমাত্র পিছলানো গতি বর্তমান যেখানে \omega = 0।
নিচের ছবি : t সময়ে কেবলমাত্র গড়ানো গতি বর্তমান যেখানে \omega = \alpha t।

লক্ষ্য করো, এখানে চল ঘর্ষণের দুটো গুরুত্বপূর্ণ অথচ বিপরীতমুখী ভূমিকা রয়েছে। একদিকে চল ঘর্ষণ গোলকের উপর মন্দন (retardation) তৈরি করে। ফলে ভরকেন্দ্রের রৈখিক বেগ ধীরে ধীরে কমে। অন্য দিকে, ভরকেন্দ্রগামী যে অক্ষ কেন্দ্র করে গোলকটি ঘোরে, চল ঘর্ষণ সেই অক্ষ সাপেক্ষে কৌণিক ত্বরণ (angular acceleration) সৃষ্টি করে। ফলে গোলকের কৌণিক বেগ ধীরে ধীরে বাড়তে থাকে।

এভাবে একটা সময় আসে গোলকটি না পিছলে কেবলই গড়াতে থাকে (rolling without slipping)। এই অবস্থায় গোলকের কেন্দ্রের রৈখিক দ্রুতি (v) = কৌণিক দ্রুতি (\omega) \times ব্যাসার্ধ (r)। দেখা যাক, এখনকার রৈখিক গতি v-এর সাথে শুরুর গতি V-এর কোনো সম্পর্ক আছে কি না।

এখানে বাধা বল:

f_k = \mu _k mg

অতএব এই বলের কারণে মন্দন,

a = \mu _k g

গোলকের উপর টর্ক যদি \tau হয়, ঘূর্নাক্ষের সাপেক্ষে জড়তা ভ্রামক যদি I হয় আর কৌণিক ত্বরণ যদি \alpha হয়, তাহলে:

\tau = I\alpha = \frac{2}{5}mr^2\alpha = f_k r

অথবা,

\frac{2}{5}mr^2\alpha = \mu _k mgr

অতএব,

\alpha = \frac{5\mu _k g}{2r}

এই \alpha কৌণিক ত্বরণের জন্যই গোলকের কৌণিক বেগ শূন্য থেকে t সময় পরে \omega হয় (শুধুমাত্র গড়ানো গতির সময়)। তাই এখানে,

\omega = 0 + \alpha t = \frac{5\mu_k gt}{2r}

বা,

t= \frac{2\omega r}{5\mu_k g} = \frac{2v}{5\mu _k g}

t-এর এই মানটি ব্যবহার করে শুরুর গতি v আর শেষের গতি V-এর মধ্যে সম্পর্কটা দেখা যায়:

v = V - at = v - \mu_k gt = V - \mu _k g\frac{2v}{5\mu _k g}

অতএব,

V = \frac{5V}{7}

এটাই গোলকের কেন্দ্রের কাঙ্ক্ষিত দ্রুতি।

শক্তির সংরক্ষণ ব্যবহার করে শুরু ও শেষের গতির সম্পর্ক স্থাপন

যান্ত্রিক শক্তির সংরক্ষণ সূত্র ব্যবহার করে এখন দেখবো, গোলকটির কেন্দ্রের বেগের এই মান সঠিক হয় কি না?

প্রথমে গোলকটির কেবলমাত্র রৈখিক বেগই ছিল, তার জন্যে রৈখিক গতিশক্তির মান \frac{1}{2}mV^2।

বেশ কিছুটা পিছলে যাওয়ার ফলে গোলকটি কেবলমাত্র গড়ানো গতি পায়। এই অবস্থায় গোলকের মোট গতিশক্তি \frac{1}{2}mV^2 + \frac{1}{2}I\omega^2।

আবার কেবলমাত্র গড়ানো গতির ক্ষেত্রে v = \omega r এবং গোলকের ভরকেন্দ্রগামী ঘূর্ণাক্ষের সাপেক্ষে জড়তা ভ্রামক হয়:

I = \frac{2}{5}mr^2

যান্ত্রিক শক্তির সংরক্ষণ সূত্র ব্যবহার করলে অঙ্কটা এরকম দাঁড়ায়:

\frac{1}{2}mV^2 = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2

\frac{1}{2}mV^2 = \frac{1}{2}mv^2 + \frac{1}{2} \times \frac{2}{5}mr^2 \times (\frac{v}{r})^2

V^2 = v^2 + \frac{2}{5}v^2

v= \sqrt{\frac{5V}{7}}

স্পষ্ট দেখা যাচ্ছে, বেগের এই মানটি আগে পাওয়া বেগের মানের সাথে মিললো না।

ভরবেগের সংরক্ষণ ব্যবহার করে শুরু শেষের গতির সম্পর্ক স্থাপন

আরো একভাবে অঙ্কটা করা যায়।

স্পর্শবিন্দুর সাপেক্ষে গোলকটির উপর নেট টর্ক শূন্য হয় (যেহেতু ঘর্ষণবল সেই স্পর্শবিন্দু দিয়েই যাচ্ছে)। ফলে স্পর্শবিন্দুর সাপেক্ষে কৌণিক ভরবেগ সংরক্ষিত হয়। সেক্ষেত্রে ঘটনাটি শুরু এবং শেষের সময় গোলকটির কৌণিক ভরবেগ একই থাকে। এই নীতি ব্যবহার করে গোলকের শেষের গতিবেগ অর্থাৎ শুধুই গড়ানোর সময় গোলকের ভরকেন্দ্রের বেগ আমরা পেতে পারি।

নিচের অঙ্কে তা করে দেখানো যায়: গোলকের প্রাথমিক কৌণিক ভরবেগ = অন্তিম কৌণিক ভরবেগ।

অর্থাৎ,  mVr = mvr  (গোলকের ভরকেন্দ্রের চূড়ান্ত কৌণিক ভরবেগ) + I\omega  (ভরকেন্দ্রের সাপেক্ষে ঐ গোলকটির চূড়ান্ত কৌণিক ভরবেগ )।

বা,

mVr = mvr + \frac{2}{5} \times mr^2 \times (\frac{v}{r}) = mvr + \frac{2}{5}mvr

\implies v = \frac{5V}{7}

আগের গণনায় আমরা গোলকটির ক্ষেত্রে দ্রুতির মান এটাই পেয়েছিলাম।

তার মানে এখানে যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা ঠিক হয়নি।

অথচ নততলে বিশুদ্ধভাবে গড়ানো গোলকটির ক্ষেত্রে যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করে আমরা কাঙ্খিত ফলাফল পেয়েছিলাম।

শক্তির সংরক্ষণ সূত্র কখন প্রয়োগ করা চলে?

তাহলে এক্ষেত্রে ভুলটা কোথায়? কিংবা বিশুদ্ধ গড়ানোর ক্ষেত্রেই বা ঘর্ষণ থাকা সত্ত্বেও কীভাবে এই সূত্রটি প্রয়োগ করা যাচ্ছে?

আমরা জেনে এসেছি ঘর্ষণ একটি অবক্ষয়ী বল, অর্থাৎ ঘর্ষণের বিরুদ্ধে কার্যকে আমরা ফিরে পেতে পারি না। তাই শক্তির সংরক্ষণ সূত্র প্রয়োগ করা যায় না।

দ্বিতীয় ঘটনাটিতে গোলকটি প্রথমে যখন পিছলে পিছলে এগিয়ে রায়, তখন পিছলানোর বিপরীতে চল ঘর্ষণ কাজ করে। এই চল ঘর্ষণের বিরুদ্ধে কাজ তাপশক্তির আকারেই খরচ হয়। তাই  পিছলানো গতি থেকে গোলকটি না পিছলে যখন শুধু গড়ানো গতি লাভ করে, তখন গোলকটির মোট গতিশক্তি আগের গতিশক্তি থেকে কমে যায়। কারণ, প্রাথমিক গতিশক্তির কিছু অংশ ঘর্ষণের বিরুদ্ধে কাজ করতে গিয়ে নষ্ট হয়ে যায়, যা আর ফিরে পাওয়া যায় না। ফলে এই ঘটনায় যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করতে গেলে একটা বিরাট ভুল হয়ে যায়। তাই এখানে যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করা উচিত নয়।

আর প্রথম ক্ষেত্রে ড্রামটির পুরো যাত্রাপথে শুধু গড়ানো গতিই রয়েছে। সেখানে স্পর্শবিন্দুতে স্থিতঘর্ষণ রয়েছে। আমরা আগেই আলোচনা করেছি এই স্থিতঘর্ষণই ড্রামটির ঘূর্ণাক্ষের সাপেক্ষে একটা টর্ক সৃষ্টি করে। ফলে ড্রামটি যত নিচের দিকে গড়াতে থাকে ততই জোরে জোরে ঘুরতে থাকে। আর শুধু গড়ানো গতির ক্ষেত্রে স্পর্শবিন্দু কখনোই পিছলে যায় না, অর্থাৎ স্থিতঘর্ষণের বিরুদ্ধে স্পর্শবিন্দুতে আপেক্ষিক সরণ ঘটে না। তাই স্থিতঘর্ষণের বিরুদ্ধে কৃতকার্য‌ও হয় না। ফলে গড়ানোর শুরুতে কিংবা শুরুর পরে যেকোনো সময়ে মোট গতিশক্তি একই থাকে ও যান্ত্রিক শক্তি সংরক্ষিত হয়। তাই এক্ষেত্রে যান্ত্রিক শক্তির সংরক্ষণ সূত্র প্রয়োগ করলে কোনো ভুল হয় না।

পরীক্ষা-নিরীক্ষার কিছু নমুনা

এতকিছু তথ্যের বুলি আওড়াতে আওড়াতে এবার অন্য কথায় আসি। বিজ্ঞান নিয়ে কিছু কথা বলতে গেলে তত্ত্ব তুলে ধরার সাথে পরীক্ষা নিয়ে কথা না বললে তা অসম্পূর্ণ।

সেই লক্ষ্যে কিছু ছোটখাটো পরীক্ষা করার চেষ্টা করেছি আমরা। অঙ্ক কষতে গিয়ে আমরা দুটি উদাহরণ তুলে ধরেছিলাম: একটি গোলক ও অন্যটি একটি ড্রাম। নততল বরাবর দুটি বস্তুকে গড়িয়ে দিয়ে বেগ, ত্বরণ ও শক্তি ইত্যাদি মাপার পরীক্ষা করতে গিয়ে আমরা ব্যবহার করেছি একটি পিতলের গোল বলকে, আর ড্রাম হিসেবে অ্যালুমিনিয়ামের তৈরি একটি চোঙ। ড্রেসিং টেবিলের আয়নার মত একটি পাতলা বেধের কাচকে ব্যবহার করে আমরা তৈরি করেছি একটি নততল।

ঘরে পরীক্ষা করার জন্য নততলের ব্যবস্থা।

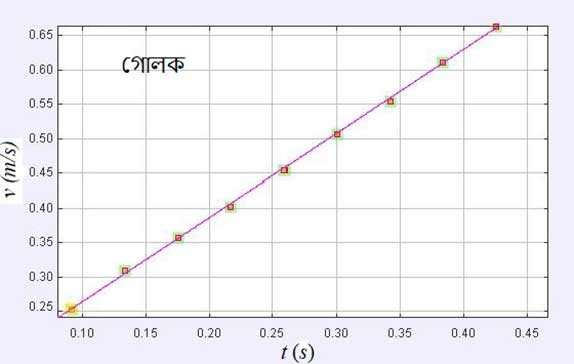
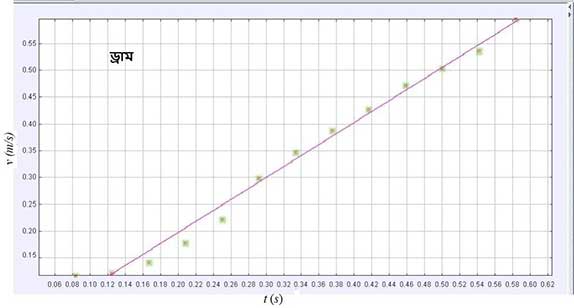
চাঁদা বসিয়ে বইপত্র দিয়ে 10 ডিগ্রি কোণে বসানো হয়েছে নততলটিকে। বস্তু নততল বরাবর কত দূরত্ব যাচ্ছে এই পরিমাপ পাওয়ার জন্য নততলের নীচে মিলিমিটার লেখ (ক্ষুদ্রতম অংশাঙ্কন মিলিমিটার সীমায়) পাশে ডবল-টেপ বা সেলোটেপ দিয়ে লাগানো হয়েছে। তারপর ঐ গোলক ও ড্রামকে নততলের চূড়ার কোনো বিন্দু থেকে তল বরাবর ফেলা হলো ও মোবাইল ক্যামেরা ব্যবহার করে গোলক (ভিডিও 1) ও ড্রামের (ভিডিও 2) গতিগুলোকে ভিডিও করে রাখা হলো। এই ভিডিওগুলোকে ‘Tracker’ নামের এক সফটওয়্যার দিয়ে আমরা বিশ্লেষণ করে সময়ের সাথে সাথে বস্তুর বেগ কত হচ্ছে, তা জানতে পারছি। ‘Tracker’ সফটওয়্যার দিয়ে গোলকের ভিডিওটি ট্র্যাক করলে দূরত্ব মাপার ক্ষেত্রে মিলিমিটার গ্রাফের এক ক্ষুদ্রতম ঘর অর্থাৎ 1 মিলিমিটারকেই আমরা প্রমাণ ধরে সময়-বেগ (t - v) লেখচিত্র এঁকে ফেলতে পারি। আর এই লেখচিত্রের নতি থেকে আমরা যথেষ্ট নিশ্চয়তার সাথেই ত্বরণের মান বের করতে পারি। সাথে আমরা স্থিতিশক্তি কিংবা গতিশক্তির পরিবর্তনের পরিমাণও গণনা করতে পারি।

বস্তুভার (g)ব্যাসার্ধ (cm)নততলের ব্যবহৃত দৈর্ঘ্য (cm)সময় (s)বেগ (cm/s)
গোলক58.271.1817.00.41765.3
ড্রাম20.920.8013.00.54250.4
টেবিল 1: গোলক ও ড্রামের কিছু ভৌত রাশি
গোলকের সময়-বেগ লেখচিত্র
ড্রামের সময়-বেগ লেখচিত্র

তাত্ত্বিক গণনা থেকে গোলকের ক্ষেত্রে ত্বরণের (a) মান = \frac{5}{7}g \sin\theta এবং ড্রামের ক্ষেত্রে ত্বরণ = \frac{2}{3}g \sin\theta। গোলক বা ড্রামের বেলায় বস্তু নততল বরাবর ক্ষেত্রে স্থিতিশক্তির (\Delta E_p) পরিবর্তন হয় = mgl \sin\theta । গতিশক্তির পরিবর্তনের পরিমাণের কথা বলতে গেলে দু ক্ষেত্রে কিন্তু তা আলাদা। গোলকের বেলায় গতিশক্তির পরিবর্তন \Delta E_k = \frac{7}{10}mv^2। আর ড্রামের ক্ষেত্রে \Delta E_k = \frac{3}{4}mv^2। নততলের কোণ 10^\circ-র ক্ষেত্রে, শুরু থেকেই গোলকটির ও ড্রামের দুক্ষেত্রে আমরা  পিছলানো গতি দেখতে পাইনি, বরং বিশুদ্ধ গড়ানো গতি দেখতে পেয়েছি। আমরা নিচের টেবিলে সব মানগুলো লিখলাম।

বস্তুপর্যবেক্ষণ
সংখ্যা		নতি থেকে a
(m/s^2)		দূরত্ব
(m)		বেগ (v)
(m/s)		\Delta E_p
(জুল)		\Delta E_k
(জুল)		গড়
\Delta E_k
(জুল)
গোলক11.220.150.600.0150.0150.015
21.220.610.015
31.230.610.015
41.230.610.015
ড্রাম11.050.560.00530.00510.0050
21.060.560.0051
31.000.550.0048
41.000.550.0048
টেবিল 2: গোলক ও ড্রামের ক্ষেত্রে বেগ, ত্বরণ, স্থিতিশক্তি ও গতিশক্তির পরিবর্তনের পরিমাপ

আলোচনার প্রথমে আসি ত্বরণের কথায়। গোলক ও ড্রামের ভিডিও ট্র্যাকিং করে আমরা ত্বরণের মান যা পাই, তা তাত্ত্বিক গণনায় পাওয়া মানের (গোলকের ক্ষেত্রে 1.216 m/s2 ও ড্রামের ক্ষেত্রে 1.12 m/s2)  সাথে প্রায় ক্ষেত্রে একটু আলাদা হয়ে যাচ্ছে। এটাই হচ্ছে তত্ত্বগত মান ও পরীক্ষালব্ধ মানের তফাৎ যা অত্যন্ত বাস্তবসম্মত। একটি পরীক্ষা করতে গেলে মাপার ক্ষেত্রে অনিশ্চয়তা অনেক জায়গায় থাকে, যা এড়ানো বেশ কঠিন। আসলে যে যন্ত্র বা যে পরিকাঠামোর মধ্যে একটা পরীক্ষা আমরা করি, এগুলো তার স্বাভাবিক সীমাবদ্ধতা।

বিশুদ্ধ গড়ানো গতির ক্ষেত্রে পিতলের গোলকের জন্য সমীকরণে a -এর মান বসালে পাই f = \frac{2}{5}mg \sin\theta। আবার এইভাবে অ্যালুমিনিয়ামের ড্রামের বেলায় এই মান, f= \frac{1}{3}mg \sin\theta। একটি কথা মনে করিয়ে দিই। স্থিত ঘর্ষণ গুণাঙ্কের সীমাস্থ মান (\mu) বের করার সময় আমরা নততলের কোণ আস্তে আস্তে পরিবর্তন করতে থাকি। যে কোণের জন্য নততলের উপর রাখা বস্তু পিছলে যাওয়ার উপক্রম হয়, তার ট্যানজেন্ট \mu-এর সমান হয়। \mu -এর মানের একটা আন্দাজ পাওয়ার জন্য আমরা একটি অ্যালুমিনিয়ামের আয়তঘনাকার ব্লক নিয়ে পরীক্ষা করে দেখলাম নততলের কোণ 15^\circ হলে বস্তুটি পিছলানোর উপক্রম করছে। তাই এক্ষেত্রে স্থিতঘর্ষণ গুণাঙ্ক, \mu = tan15^\circ = 0.27। সেক্ষেত্রে 60^\circ-র উপরে নততলের কোণ হলে গোলক বা ড্রাম নততলের উপরের দিকের কোনো বিন্দু থেকে ছেড়ে দিলে প্রথম 1 সেমি অব্দি গড়ানো ও পিছলানো গতির এক সংমিশ্রণ দেখা যায়। উপরের f-এর দুই মান তাদের নিজ নিজ ক্ষেত্রের স্থিতঘর্ষণ বলের সীমাস্থ মান (\mu mg cos\theta) -এর থেকে কম বলেইতো এই কোণের নততলে গোলকের বিশুদ্ধ গড়ানোই সম্ভব, পিছলানো গতি অসম্ভব। আর যদি f -এর থেকে বেশি হতো তাহলে শুরু থেকেই ড্রামটার পিছলানো গতি থাকতো।

বস্তুর তল বরাবর গড়ানো গতির ক্ষেত্রে আবর্ত ঘর্ষণের উপস্থিতির জন্য বিরুদ্ধ টর্ক ও  বিরুদ্ধ বলের উদ্ভব (সূত্র: University Physics with Modern Physics, H. D. Young, R. A. Freedman, 14th Ed, Pearson, 2018, p 339)।

গোলক ও ড্রামের ক্ষেত্রে ফলাফল বিবেচনা করলে দেখা যায়, গোলকের ত্বরণের তত্ত্ব থেকে হিসেবে করা মানের সাথে পরীক্ষা থেকে পাওয়া মানের তেমন তফাৎ নেই, কিন্তু তার তফাৎ দেখা যাচ্ছে ড্রামের বেলায়। আর স্থিতিশক্তির পরিবর্তনের তাত্ত্বিক মানের সাথে গতিশক্তির পরিবর্তনের গড় মানের তফাৎ (\Delta E_p - \Delta E_k) গোলকের ক্ষেত্রে শূন্য হলেও ড্রামের ক্ষেত্রে তফাৎ হচ্ছে 0.0003 জুল। অর্থাৎ এক্ষেত্রে ড্রামের যে পরিমাণ স্থিতিশক্তি কমে যাচ্ছে সেই পরিমাণ গতিশক্তি পাওয়া যাচ্ছে না। 0.0003 জুল গতিশক্তির ঘাটতি হচ্ছে। গোলকের ক্ষেত্রে এই ঘাটতিটা প্রায় নেই বললেই চলে। দেখা যাচ্ছে ড্রামের ক্ষেত্রে সামান্য পরিমাণ শক্তি নষ্ট হচ্ছে। এই পরীক্ষায় আমরা খালি চোখে গোলক এবং ড্রাম দুইয়ের ক্ষেত্রে কেবলমাত্র গড়ানো গতিই দেখতে পেয়েছি, গড়ানোর সাথে পিছলানো গতি দেখতে পাইনি। বিশুদ্ধ গড়ানো বস্তুর ক্ষেত্রে স্পর্শতলে স্থিত ঘর্ষণ কাজ করে, আর স্থিত ঘর্ষণ বলের জন্য কোনো কার্য হয় না। ফলে শক্তিক্ষয়ের কোন প্রশ্ন নেই। তবে স্বাভাবিক ভাবে মনে প্রশ্ন আসে: তাহলে আমাদের পরীক্ষায় শক্তির এই ঘাটতিটা কেন হচ্ছে? এখানে চোঙের গড়ানোর সাথে সাথে অন্য কিছু কি ঘটছে, যা আমরা খালি চোখে ধরতে পারছি না ! 

আসলে বস্তু ও নততলকে আমরা আদর্শ দৃঢ় বলে ভাবছি। কিন্তু বাস্তবে কেউই আদর্শ দৃঢ় বস্তু নয়। ফলে আবর্ত ঘর্ষণের সৃষ্টি হচ্ছে। আর আবর্ত ঘর্ষণ ড্রামের বেগ কমিয়ে দেওয়ায় গতি শক্তির ঘাটতি হচ্ছে। এবার আলোচনায় আসা যাক, আবর্ত ঘর্ষণের জন্য বেগ কিভাবে কমে  যাচ্ছে? বস্তু গড়িয়ে পড়ার সময় তলের সংশ্লিষ্ট বিন্দুর কাছাকাছি অঞ্চল একটু দুমড়ে মুচড়ে যায়, অর্থাৎ তার বিকৃতি ঘটে। এই বিকৃতির জন্য বস্তুর গড়িয়ে পড়ার সময় বস্তুর ভারকেন্দ্রগামী একটি উল্লম্ব রেখা থেকে সামনের দিকে অল্প তফাতে থাকা দূরত্বে (বিকৃতিযুক্ত অঞ্চলে) একটি নেট লম্ব প্রতিক্রিয়া কাজ করে। এই প্রতিক্রিয়ার উল্লম্ব উপাংশ উল্টো দিকে এক টর্ক সৃষ্টি করে [১], এবং অনুভূমিক উপাংশ গতির বিরুদ্ধে বাধা দেয়। এর সম্মিলিত ফল হিসেবে বস্তুর গতিবেগ‌ও ক্রমশ কমতে থাকে। ফলে গতিশক্তি কমে যায় ও শক্তিক্ষয়ের প্রসঙ্গ আসে। তবে উল্লেখ করতে হবে, এই নষ্ট হয়ে যাওয়া শক্তির মান অল্প, তা চল ঘর্ষণজনিত শক্তিক্ষয়ের থেকে অনেক কম।

কিন্তু গোলকের ক্ষেত্রেই বা গতি শক্তির তেমন কিছু ঘাটতি হচ্ছে না কেন? আদর্শ ক্ষেত্রে অর্থাৎ আদর্শ দৃঢ় গোলক এবং আদর্শ দৃঢ় নততলের বেলায়, স্পর্শবিন্দু কেবলমাত্র একটি হওয়ায় (যেহেতু কোনো বিকৃতি নেই) লম্বপ্রতিক্রিয়া গোলকের ভারকেন্দ্র বরাবর ক্রিয়া করে। তাই এক্ষেত্রে কোনো বিরুদ্ধ টর্ক  কিংবা কোনো বিরুদ্ধ বল থাকে না, অর্থাৎ আবর্ত ঘর্ষণ সৃষ্টি হয় না। ফলে, বেগও কমে না ও গতি শক্তির কোনো ঘাটতি হয় না। কিন্তু বাস্তবে, আমাদের গোলক ও নততল কোনটাই আদর্শ নয়। ফলে তলের উপর দিয়ে গোলকের গড়িয়ে যাওয়ার সময় স্পর্শবিন্দু না হয়ে একটি ছোট স্পর্শ অঞ্চল তৈরী হয়। আর গোলকের এই স্পর্শ অঞ্চল এতোটাই কম হয় যে  গতি শক্তির ঘাটতিটা ধর্তব্যের মধ্যে আসে না। কিন্তু তুলনায় ড্রামের ক্ষেত্রে স্পর্শ অঞ্চল বেশি হওয়ায় শক্তির ঘাটতিটা ধরা পড়ে, অর্থাৎ, ড্রামের ক্ষেত্রে আবর্ত ঘর্ষণের বিরুদ্ধে কৃতকার্য যথেষ্ট হয়। 

গোলকের ক্ষেত্রে গতি শক্তির সেভাবে ঘাটতি না হওয়া কিংবা ড্রামের ক্ষেত্রে গতি শক্তির সামান্য ঘাটতি প্রমাণ করে, আবর্ত ঘর্ষণ স্পর্শতলের ক্ষেত্রফলের উপর নির্ভর করে [২]।

ঋণস্বীকার: ড. সুরজিত চক্রবর্তী, অনির্বাণ ঘোষ ও অনির্বাণ গঙ্গোপাধ্যায় লেখাটির বিষয়বস্তুর সার্বিক উপস্থাপনার ক্ষেত্রে পরামর্শ ও মতামত দিয়েছেন।  আমরা আন্তরিক ভাবে কৃতজ্ঞ।

সূত্র:

[১] সৌরভ কান্তি দে ও প্রদীপ্ত পঞ্চাধ্যায়ী, গড়িয়ে চলার সময় ঘর্ষণ (ঘর্ষণের উৎস – পর্ব ৩)

[২] S. Chakrabarti, R. B. Khaparde, and A. M. H Kachwala, Experimental study of the coefficient of rolling friction of the axle of a Maxwell’s wheel on a soft horizontal surface, Eur. J. Phys. 41 (2020) 035803

https://iopscience.iop.org/article/10.1088/1361-6404/ab78a5

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/energy-momentum-conservation

print