নকশীকাঁথার মাঠ ও তার "দূরত্ব" (জ্যামিতির গোড়ার কথা - পর্ব ৬)

স্বর্ণেন্দু শীল

(Ecole Polytechnique Fédérale de Lausanne, Switzerland)

 

21 Jun 2017

Link: https://bigyan.org.in/elements-of-geometry-part-6

আগে যা হয়েছেঃ

প্রথম পর্বে আমরা শুরু করেছিলাম জ্যামিতিতে আদৌ কিছু দেওয়া আছে কিনা এই প্রশ্ন দিয়ে। দেখেছিলাম যে ইউক্লিডীয় জ্যামিতির স্বতঃসিদ্ধগুলো আসলে সেই দেওয়া থাকা জিনিসগুলো। কিন্তু কি বলছে সেগুলো? প্রথম পর্বে শুধুই প্রথম স্বতঃসিদ্ধ কি বলছে দেখেছিলাম। দ্বিতীয় পর্বে দেখেছি জ্যামিতির বীজগাণিতিকরণ হয়ে কিভাবে কার্তেসীয় স্থানাঙ্ক জ্যামিতি এল, আর এই স্থানাঙ্ক জ্যামিতির হাত ধরে আমরা দেখলাম যে দ্বিতীয়, তৃতীয় আর চতুর্থ স্বতঃসিদ্ধ কি বলছে।  ইউক্লিডীয় দূরত্ব অপেক্ষক আর ইউক্লিডীয় ইনার প্রোডাক্টকেও চিনলাম সেই পর্বেই। তৃতীয় পর্বে সমস্তটা জুড়েই আমরা মাথা ঘামিয়েছি পঞ্চম স্বতঃসিদ্ধ নিয়ে।  দেখলাম পঞ্চম স্বতঃসিদ্ধ কি বলছে আর দেখেছি সেই স্বতঃসিদ্ধকে পালটে নিলেও আমরা জ্যামিতি পাই, শুধু সেই জ্যামিতি আর ইউক্লিডীয় জ্যামিতি নয়, অনিউক্লিডীয় জ্যামিতি। চতুর্থ পর্বে আমরা দেখেছি অনিউক্লিডীয় জ্যামিতির অদ্ভুত অথচ মজার জগতটাকে। একই সাথে চতুর্থ পর্বের শেষে উঠে এসেছিল নতুন প্রশ্ন —  অনিউক্লিডীয় জ্যামিতিরও কি বীজগাণিতিকরণ সম্ভব? পঞ্চম পর্বে আমরা অনিউক্লিডীয় জ্যামিতির বীজগাণিতিকরণের দিকে এগিয়েছি। দেখেছি একটা অনিউক্লিডীয় স্থান আসলে অনেকগুলো স্থানাঙ্ক-তাপ্পি একসাথে জুড়ে বানানো একটা নকশী কাঁথা, ম্যানিফোল্ড। ওই স্থানাঙ্ক তাপ্পিগুলোর সমষ্টি বা স্থানাঙ্ক মানচিত্র দিয়ে ওই কাঁথার উপরে আঞ্চলিক স্থানাঙ্ক-তন্ত্র ও আঞ্চলিক স্থানাঙ্কের ধারণা পাওয়া যায়। এটা ব্যবহার করে অনিউক্লিডীয় স্থানেও ইউক্লিডীয় স্থানের মতই স্থানাঙ্ক জ্যামিতি করা সম্ভব, তবে শুধুই আঞ্চলিকভাবে। আবার পঞ্চম পর্বেই শেষ দিকে আমরা দেখেছি যে অনিউক্লিডীয় স্থানের প্রতিটি বিন্দুতে একটা করে লিনিয়ার স্থান থাকে। এই লিনিয়ার স্থান আসলে ওই বিন্দুতে স্পর্শক স্থান, আর এই ম্যানিফোল্ড ও তার প্রতিটি বিন্দুতে স্পর্শক স্থান একসাথে নিয়ে যে জিনিসটা, যাকে আমরা স্পর্শক গুচ্ছ বলি,  সেটা একটা বিশেষ ধরণের তন্তুগুচ্ছ (fiber bundle) —  লিনিয়ার বা ভেক্টর গুচ্ছ (vector bundle )।

এই পর্বে আমরা দেখব যে কিভাবে স্পর্শক-গুচ্ছে এমন একটা ধারণা ব্যবহার করতে পারি যা ইউক্লিডিয় স্থানে ইনার প্রোডাক্ট যে কাজটা করছিল, সেইটার বিকল্প আমাদের দেবে। সেই ধারণার নাম রীমানীয় মাপক ( Riemannian metric)।

( পঞ্চম পর্বের পর )

ইউক্লিডীয় স্থান না হলে, সমান্তরাল করে বা প্যারালাল লাইনে বয়ে যাওয়ার মানে বুঝতে অসুবিধে কোথায়?

ধরুন, p আর q দুটো আলাদা বিন্দু জমি-স্থানের ওপরে রয়েছে। p থেকে q অব্দি একটা পথ রয়েছে, যেটা পুরোটাই জমি-স্থানে আছে। আমরা p বিন্দুতে একটা স্পর্শককে (ট্যানজেন্ট-কে) নিলাম, টেনে q বিন্দুতে নিয়ে গেলাম। এমনভাবে নিয়ে গেলাম যাতে q অব্দি মাঝের সব বিন্দুতে সেটা স্পর্শকই থাকে। এই টেনে আনাটাকে সমান্তরাল পরিবহন তখনই বলব যখন এই স্পর্শকটা মাঝের সব বিন্দুতে (আর q বিন্দুতেও) শুরুর স্পর্শকটার ‘সমান্তরাল’ হবে।

ঝামেলাটা এখানেই, কারণ p বিন্দুতে স্পর্শক আছে p বিন্দুর স্পর্শক স্থানে, আর q বিন্দুতে স্পর্শক আছে q বিন্দুর স্পর্শক স্থানে। এই দুটো স্পর্শক যদি একই স্থানে থাকত, তাহলে সেই স্থানে দুজনে পরস্পর সমান্তরাল কিনা, আমরা সহজেই সেটা নির্ণয় করতে পারতাম। জমি-স্থানটা ইউক্লিডীয় স্থান হলেও এটা পারি, কারণ দুটো স্পর্শকই জমি-স্থানটায় রয়েছে। কিন্তু ইউক্লিডীয় স্থান না হলে পারার সম্ভাবনা নেই, কারণ সাধারণভাবে এরকম কোন একটা স্থান থাকবে না যেখানে দুটো স্পর্শকই রয়েছে। গোলকের উপরিতলের উদাহরণটা ভাবলেই বুঝবেন, কেন এমন কোনো স্থান নেই যাতে দুটো স্পর্শক-ই থাকতে পারে। আসলে একটা আছে, সেটা হল গোলকটাকে আমরা যে ত্রিমাত্রিক ইউক্লিডীয় স্থান থেকে দেখছি সেইটা, আর সেইটাই একমাত্র। কিন্তু যার ওপরে জ্যামিতি করছি তার বাইরে কি আছে, এটা নিয়ে যে আমরা মোটেই মাথা ঘামাবো না, সেটা আগেই ঠিক করেছি। তাই সেই ত্রিমাত্রিক ইউক্লিডীয় স্থানটা বাদ।

কিন্তু তাহলে উপায়? দুটো আলাদা আলাদা স্থানে থাকা দুটো ভেক্টর পরস্পর সমান্তরাল কিনা এ প্রশ্ন অর্থহীন। সেটা এক জাতের আলু আর এক জাতের পটলের মধ্যে তুলনা করার মতো হবে। দুটো ভিন্ন জাতের আলু বা দুটো ভিন্ন জাতের পটলের মধ্যেই শুধু এই তুলনা করা সম্ভব।   

উপায় একটা আছে, একেবারে নিরাশ হয়ে পড়ার মত নয় অবস্থাটা। হাজার হোক, দুটো স্পর্শক স্থানই একই স্থানের কপি বা নকল। কপিই যদি হয়, তাহলে p বিন্দুতে স্পর্শক স্থানের একটা ভেক্টরের কপি q বিন্দুর স্পর্শক স্থানে কোথাও না কোথাও আছে, তাই না? যতই অগোছালো বাঁধাই হোক, সবকটা পাতাই যখন একই পাতার ফটোকপি তখন একটা পাতার কোন একটা অক্ষরের কপি অন্য পাতাটায় নিশ্চয়ই আছে। সে যেখানেই থাকুক না কেন, আছে।

এবার ভাবুন যে একটা স্পর্শক স্থানে সবকটা ভেক্টরের কপি অন্য একটা স্পর্শক স্থানে কোথায় আছে, সেটা আপনি জানেন। এর মানে আপনি জানেন যে একটা স্পর্শক স্থানকে টেনে কিভাবে আর একটার সাথে মিলিয়ে দেবেন। এই জিনিসটাকে, মানে এইরকম কোন ফর্মুলা বা নিয়ম, যা আপনাকে বলে দেবে একটা স্পর্শক স্থানকে কিকরে আর একটার সাথে মিলিয়ে দেবেন, তাকে অঙ্কের ভাষায় বলে সংযোগ বা কানেকশন ( connection )।

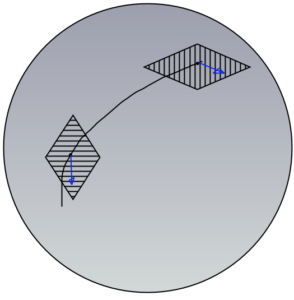
আসলে সংযোগ যে শুধু স্পর্শক স্থানেই হয় এমন নয়, যেকোন তন্তুগুচ্ছতেই হতে পারে। ধরুন, আপনি জমি-স্থানের উপর কাছাকাছি দুটো বিন্দু নিলেন। সেই বিন্দুদুটোর ওপরের তন্তুদুটোকে কিভাবে মেলাবেন, সেই নিয়মটাই হল ওই তন্তুগুচ্ছের ওপরে একটা সংযোগ ( connection on the fiber bundle)। তন্তুগুচ্ছটা যদি লিনিয়ার গুচ্ছ হয় তাহলে তার ওপরে সংযোগটারও কিছু বিশেষ ধর্ম থাকতে হবে। সেই ধর্মগুলো থাকলে সেই সংযোগগুলোকে বলে লিনিয়ার সংযোগ বা অ্যাফাইন সংযোগ (linear connection or affine connection)। তবে আমরা যেকোনরকম তন্তুগুচ্ছে সংযোগ নিয়ে এখানে মাথা ঘামাব না। এমনকি যেকোন রকম লিনিয়ার গুচ্ছে সংযোগ নিয়েও না। আপাতত এখানে আমরা শুধু স্পর্শক গুচ্ছের লিনিয়ার সংযোগ নিয়েই ভাবব।

এবার সমান্তরাল-এর সংজ্ঞা দেওয়ার সমস্যাটাতে ফিরে আসি। একটা ভেক্টরের কপি অন্য স্পর্শক স্থানে কোথায় আছে সেটা জানলেই আমাদের ঝামেলা মিটে গেল। p বিন্দুতে একটা স্পর্শক আর q বিন্দুতে একটা স্পর্শককে সমান্তরাল তখনই বলব যখন p বিন্দুর স্পর্শক স্থানে q বিন্দুর স্পর্শকের কপিটাই হচ্ছে p বিন্দুর স্পর্শক। এইভাবে সমান্তরালের একটা মানে তৈরী করলে আমরা সমান্তরাল সংবহনেরও একটা মানে দিতে পারি। 

এক কথায়, আমরা p বিন্দু থেকে q বিন্দুতে একটা পথ বরাবর সমান্তরাল সংবহনের মানে দিতে পারি যদি তাদের স্পর্শক স্থানের মধ্যে লিনিয়ার সংযোগটা আমাদের জানা থাকে। উল্টোটাও আসলে সত্যি। যেকোন দুটো কাছাকাছি বিন্দুর মধ্যে যেকোন পথ বরাবর সমান্তরাল সংবহন মানে কি সেইটা যদি আমরা জানি, তাহলে লিনিয়ার সংযোগটাও আমরা বার করতে পারি। কিন্তু অঙ্ক কষে প্রমাণ করা ছাড়া সেটা বোঝার কোন সহজ রাস্তা নেই।

 কাকে বলব সমান্তরাল?

এইবারে আমরা আর একটু খুঁটিয়ে দেখব সমান্তরাল পরিবহন ব্যাপারটাকে। ইউক্লিডীয় স্থানেও ব্যাপারটার মধ্যে নানান মজা আছে, প্রথমে আমরা সেইটা একটু তলিয়ে ভাবব। আগে নিচের ছবি তিনটে দেখে নেওয়া যাক। তিনটে ছবিই দ্বিমাত্রিক ইউক্লিডীয় স্থানে বা দ্বিসমতলে একটা পথ বরাবর একটা স্পর্শককে টেনে নিয়ে যাওয়ার ছবি।

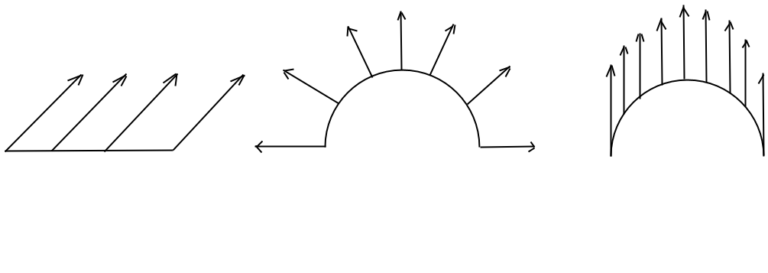
ছবিটা দেখে আপনাদেরও কি মনে হচ্ছে না যে সবচেয়ে বাঁদিকের ছবিটা আর সবচেয়ে ডানদিকের ছবিটা সমান্তরাল পরিবহন, আর মাঝেরটা নয়?

এইবারে আমরা একটা সহজ পরীক্ষা করব। কল্পনা করুন, আপনি তিনটে ছবির ক্ষেত্রেই সবচেয়ে বাঁদিকের বিন্দুতে পথটার দিকে মুখ করে দাঁড়িয়ে আছেন। আপনার বাঁহাতটা আপনার বাঁদিকে মাটির সমান্তরালে মেলে ধরুণ, ঐ বিন্দুতে স্পর্শক ভেক্টরটা বরাবর। এবার আপনি ওই পথ বরাবর হেঁটে যান, হাতটাকে আপনার শরীরের সাপেক্ষে না নড়িয়ে। পথের শেষে শুধু ডানদিকের ছবিটার ক্ষেত্রে আপনার হাতটা যেদিকে আর স্পর্শক ভেক্টরগুলো যেদিকে, সেইটা মিলবে না।  

সবচেয়ে ডানদিকের ছবিতে আপনার বাড়ানো হাত আর নাকের মধ্যে কোণটা শুরুতে ছিল শূন্য। সমান্তরালে টেনে নিয়ে গেলেন অথচ কোণটা ডানদিকের ছবিতে পালটে গেল কেন? বাঁদিকের ছবিতে তো কোণ পালটায়নি বটেই, মাঝের ছবিতেও পালটায় নি, ঐ পথের সব বিন্দুতেই সেটা এক সমকোণ। তাহলে কি ডানদিকের ছবিটা সমান্তরাল সংবহন নয়? সেটাও নয়!! আসলে মাঝেরটাও একটা ‘সমান্তরাল সংবহন’, ডানদিকের ছবিটা আর একটা ‘সমান্তরাল সংবহন’। একটা জ্যামিতিক স্থানে সমান্তরাল সংবহন অনেক রকম হতে পারে। একটু বাদে আমরা দেখব তার মধ্যে একটা একটু বিশেষ সম্মান পাওয়ার যোগ্য। সবচেয়ে ডানদিকের আর সবচেয়ে বাঁদিকের ছবিটা ইউক্লিডীয় স্থানে সেই বিশেষ সমান্তরাল সংবহনটা।

সেই বিশেষ সংবহনকে চিনবো কিভাবে? চিনবো এইভাবে: একটার জায়গায় আমরা যদি দুটো স্পর্শক নিয়ে শুরু করি আর দুটোকে যদি সমান্তরাল সংবহনের মাধ্যমে আর একটা বিন্দুতে নিয়ে যাই, তাহলে তাদের মধ্যের কোণটা পাল্টাবে না।

কি মুশকিল! এখুনি যে বললাম ডানদিকের ছবিটা সেই বিশেষ সমান্তরাল সংবহন, অথচ নাক আর হাতের মধ্যে কোণ তো পালটে গেছে!! হ্যাঁ পালটে গেছে কারণ আপনার হাত বরাবর ভেক্টরটা সমান্তরাল সংবহন হয়েছে, কিন্তু পথটা বাঁকা বলে আপনার নাক বরাবর ভেক্টরটার আদৌ সমান্তরাল সংবহন হয়নি। ইউক্লিডীয় স্থানে যেকোন বাঁকা পথ ধরে হাঁটলে কখনোই আপনার নাক বরাবর ভেক্টরটার সমান্তরাল সংবহন হবে না। একমাত্র সরলরেখা বরাবর হাঁটলেই তা সম্ভব।

এইবারে আবার উপরে বাঁদিকের ছবিটা দেখুন। সেখানে পথটা সরলরেখাংশ, তাই আপনি সেই পথ ধরে হেঁটে গেলে নাক বরাবর ভেক্টরটার সমান্তরাল সংবহন হবে। এইবারে অন্য যেকোন স্পর্শক ভেক্টরকে সমান্তরাল সংবহন করে দেখুন। ওই ক্ষেত্রে আপনার নাক আর সেই ভেক্টরটার মধ্যের কোণ পাল্টাবে না। নিচে একটা বাঁকা পথে আপনার নাক বরাবর ভেক্টরটার সমান্তরাল সংবহন করলে কি হত আর আপনি পথটা দিয়ে হেঁটে যাওয়ায় কি হচ্ছে তার একটা ছবি দেওয়া হল। এইটা দেখলেই বুঝবেন কেন বাঁকা পথে হেঁটে গেলে কখনোই নাক বরাবর ভেক্টরটা সমান্তরালে সংবাহিত হচ্ছে না।  

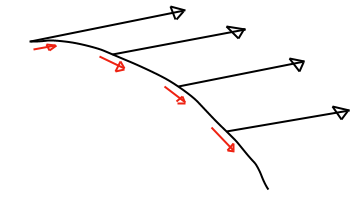
এই যে ইউক্লিডীয় স্থানে একমাত্র সরলরেখাংশ বরাবর হাঁটলেই নাক বরাবর ভেক্টরটা সমান্তরালে সংবাহিত হয়, আবার সরলরেখারাই ইউক্লিডীয় স্থানের জিওডেসিক, এইটা কি কাকতালীয়? একদম নয় !! এইখানেই ওই বিশেষ সমান্তরাল সংবহনের বিশেষত্বটা।

এবার আমরা ভাবব ইউক্লিডীয় স্থান নয় এমন জমি-স্থানে কিভাবে এই বিশেষ সংবহনটা চিনব। সেটা চেনা প্রয়োজন, নাহলে একটা বিন্দুতে দুটো স্পর্শকের মধ্যে কোণ মাপব কিভাবে? তারা যদিও সবসময় একই লিনিয়ার স্থানে থাকে ( সেই বিন্দুতে স্পর্শক স্থানটা), একমাত্র সেই বিশেষ সংবহনটার ক্ষেত্রেই তাদের মধ্যে কোণ পরিবর্তন হবে না। 

রীমানীয় ‘ম্যানিফোল্ড’

কোণ কিভাবে মাপব এর উত্তর আমরা আগেই জানি, ইনার প্রোডাক্ট দিয়ে। আমরা এই স্পর্শক স্থানের আলোচনা করতে শুরুই করেছিলাম ইনার প্রোডাক্ট বসানোর জন্যে লিনিয়ার স্থান কোথায় পাব, এই প্রশ্ন দিয়ে। এখন প্রত্যেকটা বিন্দুতে একটা করে লিনিয়ার স্থান পেয়েছি এবং সেই স্থানগুলোয় কোণ কিভাবে মাপব এই প্রশ্নটার সামনে এসে দাঁড়িয়েছি। এতক্ষণে আমরা দুইয়ে দুইয়ে চার করার জায়গায় এসেছি আর সেইটাই রীমানের উত্তরটা।

প্রতিটি স্পর্শক স্থানে যদি আমরা একটা করে ইনার প্রোডাক্ট দিতে পারি, তাহলেই আমাদের সমস্যা মিটে গেল। ঠিক সেইটাই করব আমরা। অর্থাৎ এখন p বিন্দুতে স্পর্শক স্থানে u আর v যদি দুটো স্পর্শক হয়, তাহলে তাদের মধ্যে কোণ হবে:

যেখানে আগের মতই

 একটা সিমেট্রিক, পজিটিভ-ডেফিনিট ম্যাট্রিক্স। তফাত শুধু এইটা যে আগের মত আর একটা ম্যাট্রিক্স নেই, প্রতিটি বিন্দুতে একটা ম্যাট্রিক্স। -রা এখন আর বাস্তব সংখ্যা নয়, বরং ফাংশন, প্রতিটি বিন্দুতে যাদের মান একটা বাস্তব সংখ্যা।

আরও একটা জিনিস দরকার অবশ্য, এই ফাংশনগুলোকে স্মুদ, মানে মসৃণ হতে হবে। অর্থাৎ ফাংশনগুলোর গ্রাফটা দেখতে মসৃণ, খোঁচা নেই। এইগুলো আর একটা ইনার প্রোডাক্ট নয়, প্রতিটি বিন্দুতে স্পর্শক স্থানে একটা করে ইনার প্রোডাক্ট। আমরা একটা ইনার প্রোডাক্টের পরিবার পাই ( a family of inner products) যা মসৃণভাবে, সাবলীলভাবে পালটায় নিচের বিন্দুটা পাল্টানোর সাথে সাথে, যাকে অঙ্কের ভাষায় বলে smoothly varying। সংক্ষেপে বললে, a smooth family of inner products। স্পর্শক গুচ্ছের ওপরে এরকম একটা মসৃণ ইনার প্রোডাক্টের পরিবারকে বলা হয় রীমানীয় মাপক বা রীমানীয় মেট্রিক ( Riemannian metric ), আদরের ডাকনাম মেট্রিক টেনসর ( metric tensor)।

একটা মসৃণ কাঁথা, মানে একটা স্মুদ ম্যানিফোল্ডকে জমি-স্থান হিসেবে নিয়ে তার স্পর্শক-গুচ্ছে একটা রীমানীয় মাপক দেওয়া থাকলে সেই পুরোটাকে একসাথে আমরা রীমানীয় কাঁথা বা রীমানীয় ম্যানিফোল্ড (Riemannian manifold) বলি।

বস্তুত এটাই জ্যামিতিতে দেওয়া থাকা জিনিসটা, যেটা দেওয়া থাকলেই এর ওপর জ্যামিতি কেমন দেখতে হবে সবটা শুধু হিসেব কষেই বার করা যায়।  

মেট্রিক থেকে দূরত্ব অপেক্ষক

রীমানীয় মাপক এর নাম মাপক কেন? দুটো স্পর্শকের মধ্যে কোণ মাপছে তো স্পষ্ট, কিন্তু আর কিছু মাপছে কি? দ্বিতীয় পর্বেই আপনাদের দেখিয়েছিলাম কিভাবে স্পর্শক স্থানে কোণ মাপছে মানেই স্পর্শক স্থানে দূরত্বও মাপছে। এইবারে আমরা দেখব যে স্পর্শক স্থানে দূরত্ব মাপতে পারা মানেই আসলে জমি-স্থানেও দূরত্বও মাপতে পারা।

কিভাবে? ধরা যাক জমি-স্থানে একটা বিন্দু চলছে,  সময়ে তার অবস্থান হচ্ছে , যেখানে  একটা মসৃণ ফাংশন। প্রতিটা সময় এর জন্যে এই বিন্দুগুলোকে জুড়লে যেটা পাব সেইটা জমি-স্থানে ওই বিন্দুর চলার পথটা। তাই   বলতে অনেক সময় পথটাকেও বোঝানো হয়, মোটামুটি একই কথা ।

সে যাই হোক, এইবারে আমরা এই পথ বরাবর দূরত্ব অর্থাৎ পথটার দৈর্ঘ্য মাপতে চাই। কিভাবে মাপব? প্রতিটা সময়  তে, ওই পথের স্পর্শক হচ্ছে  , মানে কে এর সাপেক্ষে অবকলন বা ডিফারেন্সিয়েট করে যা পাই। -র মান আমরা মাপতে পারি রীমানীয় মাপকটা ব্যবহার করে, তারপর সেই মানটাকে এর সাপেক্ষে সমাকলন বা ইন্টিগ্রেট করলেই পুরো পথটার দূরত্ব পেয়ে যাব। অঙ্কের ভাষায় লিখলে  সময় থেকে  সময়ের মধ্যে বিন্দুটা কতটা দূরত্ব অতিক্রম করবে তার ফর্মুলা হচ্ছে:

যেখানে | | চিহ্নটার মানে হচ্ছে নর্ম, যেটা আমরা বার করতে পারব রীমানীয় মাপকটা দিয়ে। কিকরে বার করবো, সেই ফর্মুলাটাও দেওয়া ওপরের ডানদিকে। অর্থাৎ রীমানীয় মাপক দিয়ে আমরা জমি-স্থানে যেকোন দুটো বিন্দুর মধ্যে যেকোন একটা পথের দৈর্ঘ্য মাপতে পারি। তাই কোন পথটা হ্রস্বতম সেটাও বার করতে পারি, অর্থাৎ বার করতে পারি কারা জমি-স্থানের জিওডেসিক।     

মাপক আর সংযোগের মিতালি

এখন আমরা সহজেই বুঝতে পারব, ওই বিশেষ সমান্তরাল সংবহনটা কি করে চিনব।

আগেই বলেছি সমান্তরাল সংবহনটা এমন যাতে একটা বিন্দুতে দুটো স্পর্শককে অন্য একটা বিন্দুতে সংবাহিত করলে স্পর্শক দুটোর মধ্যে কোণ পাল্টায় না। কোণ মাপতে যেহেতু এখন কোন অসুবিধে নেই, রীমানীয় মাপকটাকে ব্যবহার করেই সেটা করা যাবে। এই সমান্তরাল সংবহনটা যে সংযোগ থেকে আসে সেইটা কেমন? সেটাও বোঝা সহজ, কোন একটা স্পর্শক স্থানে দুটো স্পর্শকের মধ্যে যে কোণ, অন্য একটা স্পর্শক স্থানে তাদের কপির মধ্যেও কোণটা একই। আমরা এমন একটা লিনিয়ার সংযোগ দেখতে পাচ্ছি যা রীমানীয় মাপকটার কথাও ভাবে। এই সংযোগের সাহায্যে আমরা প্রত্যেকটা স্পর্শক স্থানকে শুধু লিনিয়ার স্থান হিসেবে একে অপরের কপি নয়, বরং ইনার প্রোডাক্ট স্থান হিসেবে কপি ভাবতে পারি।

বস্তুত এইরকম সংযোগের আরও একটা ধর্ম আছে: কোন স্পর্শক স্থানের সাপেক্ষেই একটা স্পর্শকের কপি মোচড় খেয়ে নেই। এই ধর্মটা থাকলে তেমন সংযোগের পোশাকী নাম মোচড়-ছাড়া সংযোগ বা টরশন-ফ্রি কানেকশন (torsion-free connection )। এমন কোন মোচড়-ছাড়া সংযোগ যা কোন একটা মাপকের কথা মাথায় রাখে, তাকে সাধারণভাবে মাপক সংযোগ বা মেট্রিক কানেকশন বলা হয়। রীমানীয় ম্যানিফোল্ডের স্পর্শকগুচ্ছে এরকম মাপক সংযোগ, যা রীমানীয় মাপকটার কথা ভাবে, তাকে বলা হয় লেভি-চিভিতা সংযোগ (Levi-civita connection)। এইরকম সংযোগের বিশেষ গুরুত্ব এখানেই যে যেকোন রীমানীয় কাঁথায় একটা আর একটামাত্রই লেভি-চিভিতা সংযোগ আছে। এই তথ্যটা প্রমাণ করা যায় অবশ্যই, কিন্তু সেজন্যে অনেক আঁক কষতে হয়। সেই উপপাদ্যটার নাম রীমানীয় জ্যামিতির মূল উপপাদ্য ( fundamental theorem of Riemannian geometry)।    

নাক বরাবর সোজা

আচ্ছা এবার ধরা যাক, আপনাকে কেউ বলল নাক বরাবর সোজা যেতে। ইউক্লিডীয় স্থানে এর মানে কি আমরা সবাই বুঝি, কিন্তু বাঁকা স্থানেও কি এর কোন মানে হয়? আমি যদি নাক বরাবর সোজা হাঁটতে থাকি, তাহলে আমার যাওয়ার পথটা কি ‘সরলরেখাংশ’ হবে, এমনকি বাঁকা স্থানেও?

এর উত্তরটা বেশ চমকপ্রদ। বাঁকা স্থানেও আমরা নাক বরাবর সোজা কথাটার মানে দিতে পারি, আর সেই অর্থে নাক বরাবর সোজা হাঁটলে আমার যাওয়ার পথটা ‘সরলরেখাংশ’ও হবে!! 

আচ্ছা সোজা মানে ঠিক কি? এইভাবে ভাবতে পারি, সোজা হাঁটছি মানে আমার নাকটা দিক পরিবর্তন করছে না, মানে প্রতিটি বিন্দুতেই আমার নাকটা তার আগের অবস্থানের সমান্তরাল আছে, তাই না? তাহলে সমান্তরালে থাকা ব্যাপারটার যখন বাঁকা স্থানেও একটা মানে দিতে পারি, এইভাবে নাক বরাবর সোজা কথাটার মানে দেওয়া যাবে না? একদমই যাবে আর ঠিক এইভাবেই!

কোন একটা পথের ক্ষেত্রে যদি পথের স্পর্শকটা পথ বরাবর সমান্তরাল সংবাহিত হয় তাহলে সেরকম পথকে বলব আমরা স্ব-সমান্তরাল পথ ( auto-parallel curves )। নাক বরাবর সোজা হাঁটা মানে আসলে একটা স্ব-সমান্তরাল পথ ধরে হাঁটা! আর লেভি-চিভিতা সংযোগের সমান্তরাল পরিবহনের সাপেক্ষে স্ব-সমান্তরাল পথ মানেই সেই পথটা রীমানীয় কাঁথাটার জিওডেসিক !!!

এইটা সামান্য কলনবিদ্যা কাজে লাগিয়ে সহজেই প্রমাণ করা যায়, কিন্তু ধারণাগতভাবেও বোঝা যায়। একটা বিন্দু থেকে আর একটা বিন্দুতে যেতে কোন পথে গেলে সবচেয়ে কম দূরত্ব অতিক্রম করতে হবে? সোজাসুজি গেলে, অর্থাৎ যতদূর সম্ভব সোজা একটা বিন্দু থেকে অন্য বিন্দুটায় গেলে। ঘুরপথে গেলেই বেশী হাঁটতে হবে। এখানেও তাইই হচ্ছে আসলে। সবচেয়ে ‘সোজা’ পথটাই সবচেয়ে কম দূরত্বের পথও। আর বাঁকা স্থানে জিওডেসিকরাই ‘সরলরেখা’। তাই আপনি ‘নাক বরাবর সোজা’ গেলে আপনার পথটাও ‘সরলরেখাংশ’, এমনকি বাঁকা স্থানেও। শুধু ‘সরলরেখাংশ’ গুলো আর সাধারণ কথ্য অর্থে সরলরেখাংশ নয়, এই যা তফাত।   

এভাবেও ফিরে আসা যায়

আমরা আমাদের আলোচনার একদম শেষে এসে পৌঁছেছি। স্থানের বক্রতার জন্য কত অদ্ভুত আর মজার মজার জিনিস ঘটতে পারে, তার একটা উদাহরণ দিয়ে আমরা শেষ করব। আচ্ছা, যদি আমরা এমন একটা পথ নিই, যে পথটা একটা বিন্দু থেকে শুরু হয়ে সেই বিন্দুতেই শেষ হয়েছে, আর সেই পথ বরাবর যদি একটা স্পর্শক ভেক্টরকে সমান্তরাল সংবাহিত করি, সেই ভেক্টরটার কি হবে? সাধারণভাবে মনে হয় শুরুর স্পর্শক ভেক্টরটাই ফেরত পাব। ইউক্লিডীয় স্থানে এই উত্তরটা ঠিকও। কিন্তু এক এবং একমাত্র ইউক্লিডীয় স্থানেই ঠিক!!

বাঁকা স্থানে ফিরে আসার পর কখনোই একই ভেক্টর ফেরত পাব না!! কতটা তফাত হবে সেটা নির্ভর করবে স্থানটার বক্রতার ওপর, আর পথটার ওপর। এই তফাতটাকে ওই পথটার হলোনমি (holonomy around the path) বলা হয়। নিচের ছবিতে আমরা গোলকের উপরিতলে একটা পথের হলোনমি দেখবো।

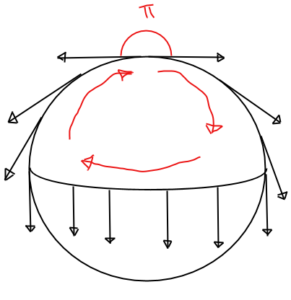
উপরের ছবিতে প্রথমেই যে প্রশ্ন মনে জাগা স্বাভাবিক, সেটা হল: কিকরে জানলাম যে ‘উত্তর মেরু’ থেকে শুরু করে স্পর্শকটা গোলকের উপর ওই বিশেষ সমান্তরাল পরিবহনটা (লেভি-চিভিতা সংযোগ) মেনে যখন ফিরে আসে, সেই সংবহনটাই ছবিতে দেখানো সমান্তরাল সংবহনটা?এর একটা উত্তর অবশ্যই আঁক কষে, কিন্তু তা ছাড়াও উত্তর দেওয়া যাবে। একটু আগেই আমরা দেখেছি যে দুটো স্পর্শক ভেক্টরের লেভি-চিভিতা সংযোগ থেকে আসা সমান্তরাল পরিবহনে তাদের মধ্যের কোণ পালটায় না। আরও দেখেছি যে স্ব-সমান্তরাল পথের স্পর্শক পথের সাথে সমান্তরালভাবে সংবাহিত হয়। স্ব-সমান্তরাল পথ কারা? জিওডেসিকরা।

এরপরে বাকিটা সহজ। পথটা আর একবার দেখুন। পথটার তিনটে আলাদা আলাদা অংশ আছে। তিনটে অংশই গোলকের উপরে জিওডেসিক কারণ তারা তিনজনেই মহাবৃত্তের অংশ, যদিও তিনজনে তিনটে আলাদা আলাদা মহাবৃত্তে রয়েছে। 

এইবারে ভেক্টরটাকে লক্ষ্য করুন। উত্তর মেরুতে সেটা ডানদিকের দ্রাঘিমারেখাটার স্পর্শক। যেহেতু দ্রাঘিমারেখাটা জিওডেসিক, তাই স্ব-সমান্তরাল। ওই ভেক্টরটাকেও সমান্তরাল সংবাহিত হতে গেলে তাইই থাকতে হবে, তাই নিরক্ষরেখা অবধি নেমে আসা পর্যন্ত তাইই রয়েছে। এরপর পথটা নিরক্ষরেখা বরাবর। আর ডানদিকের দ্রাঘিমারেখাটা যখন নিরক্ষরেখায় পড়েছে তখন ভেক্টরটা নিরক্ষরেখার সাথে লম্ব, নিচের দিকে। আবার নিরক্ষরেখা জিওডেসিক বলে এই কোণটা একই থাকতে হবে নিরক্ষরেখা বরাবর সমান্তরাল সংবহন হতে গেলে। ঠিক তাইই থেকেছে ভেক্টরটা বাঁদিকের দ্রাঘিমারেখা পর্যন্ত। এইবারে নিরক্ষরেখা যেখানে বাঁদিকের দ্রাঘিমারেখায় মিলেছে সেখানে ভেক্টরটা বাঁদিকের দ্রাঘিমারেখার স্পর্শকের ঠিক উলটো। খেয়াল করুণ দ্রাঘিমারেখা বরাবর আমরা নিচে থেকে ওপরে যাব, তাই স্পর্শক ওপরদিকে, আর ভেক্টরটা নিচের দিকে। সেই কোণটাও পাল্টাতে পারে না দ্রাঘিমারেখাটাও জিওডেসিক বলে। আর তাই উত্তর মেরুতে যখন ফিরে এলাম, ভেক্টর উলটে গেছে ১৮০ ডিগ্রী!!!

অন্য পথ বেছে নিলে কোণের তফাতটা ১৮০ ডিগ্রী নাও হতে পারত, কিন্তু কখনোই তফাতটা শূন্য হত না। এই শূন্য না হওয়াটার কারণ গোলকের উপরিতলের বক্রতা। ওই স্থানের রীমানের বক্রতা টেনসর (Riemann’s curvature tensor), যা ওই স্থানের বক্রতার একটা পরিমাপ, সেটা জানা থাকলে যেকোন পথের হলোনমি অঙ্ক কষে সহজেই বার করা যায়। আবার মেট্রিক টেনসরটা জানা থাকলে রীমানের বক্রতা টেনসরটাও অঙ্ক কষে বার করা যায়। এই রীমানীয় মেট্রিক টেনসর ও রীমানের বক্রতা টেনসর আবিষ্কারই রীমানের অবকলন জ্যামিতিতে (differential geometry) সবচেয়ে বড় অবদান। বক্রতার অবশ্য আরও নানারকম পরিমাপ ব্যবহার হয় অঙ্কে, সেগুলো সবই কোন না কোনভাবে সম্পর্কিত। অর্থাৎ, রীমানের বক্রতা টেনসরটা জানা থাকলে সেগুলোও বার করা যায়। সেগুলোর মধ্যে সবচেয়ে পরিচিত ও বহুল ব্যবহৃত পরিমাপটার নাম রিচি বক্রতা টেনসর বা Ricci curvature tensor।

সাধারণ অপেক্ষবাদের সঙ্গে পরিচিতি আছে যাদের তাদের হয়ত এই নামটা মনে পড়বে। সাধারণ অপেক্ষবাদের মূল সূত্র, যা আইনস্টাইন-হিলবার্ট ক্ষেত্র সমীকরণ  (Einstein-Hilbert field equation) নামে বিখ্যাত, তাতে চতুর্মাত্রিক স্থান-কাল সন্ততির ( four dimensional space-time continuum ) রিচি বক্রতা টেনসর ও মেট্রিক টেনসর দুটোরই দেখা মেলে। সাধারণ অপেক্ষবাদে মহাকর্ষ এই স্থান-কাল সন্ততির বক্রতারই একটা প্রতিফলন মাত্র।  

আর তাই জ্যামিতিতে দেওয়া জিনিস আসলে একটাই, একটা ম্যানিফোল্ড ও তার মেট্রিক টেনসর!

(সমাপ্ত)

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/elements-of-geometry-part-6

print