ইউক্লিডীয় স্ববিরোধিতা থেকে অইউক্লিডীয় জ্যামিতির জন্ম (জ্যামিতির গোড়ার কথা - পর্ব ৩)

স্বর্ণেন্দু শীল

(Ecole Polytechnique Fédérale de Lausanne, Switzerland)

 

05 Jul 2015

Link: https://bigyan.org.in/elements-of-geometry-part-3

এইবারে আমরা ঢুকব ইউক্লিডের পঞ্চম স্বতঃসিদ্ধের আলোচনায়। একবার দেখে নি কি বলছে এই স্বতঃসিদ্ধ।

একটি সরলরেখা অন্য দুটি সরলরেখাকে ছেদ করলে, যদি কোন একটি দিকে অন্তর্বর্তী কোণদ্বয়ের যোগফল দুই সমকোণের কম হয়, তবে সরলরেখাদুটিকে অনির্দিষ্টভাবে বর্ধিত করলে সেই দিকে মিলিত হবে।

ইউক্লিড ভেবেছিলেন যে এটা একটা উপপাদ্য। অর্থাৎ, এটাকে অন্য স্বতঃসিদ্ধগুলো থেকে প্রমাণ করা সম্ভব। কিন্তু দীর্ঘদিন ধরে কেউ এটা প্রমাণ করতে পারেনি। এই প্রমাণ করার চেষ্টার মধ্যে দিয়েই একদিন বোঝা গেল যে এটাও জ্যামিতিতে একটা দেওয়া জিনিস। অন্য স্বতঃসিদ্ধগুলো থেকে আসে না। কিভাবে বোঝা গেল, সেটা বুঝতে আমাদের কয়েকটা সংজ্ঞা জানতে হবে।

১. সরলরেখা বা লাইন — আবার মনে করিয়ে দিচ্ছি: যে সংজ্ঞা আমরা এখানে দেখব, তা গাণিতিকভাবে নিখুঁত কোন সংজ্ঞা নয়। বস্তুত কোন সংজ্ঞাই নয়। জ্যামিতিতে বিন্দুর মতই সরলরেখাও একটা অসংজ্ঞায়িত ধারণা। তবু সেই ধারণাটাকে বুঝতে আমরা কিছু একটাকে, যাকে এই ধারণাটার ব্যাখ্যা বলা যেতে পারে, সংজ্ঞা বলে চালাব।

যেকোনো দুইটি বিন্দুর মধ্যে হ্রস্বতম দূরত্বের পথটিকে ওই দুইটি বিন্দু দিয়ে যাওয়া সরলরেখাংশ বলা হয়। যেকোনো সরলরেখাংশকে দুইদিকে অসীমভাবে বর্ধিত করলে একটি সরলরেখা পাওয়া যায়।

২. সমান্তরাল সরলরেখা বা প্যারালাল লাইন — এটা ইউক্লিডেও যা, আজও সেই সংজ্ঞাটাই ব্যবহার করি আমরা। এই সংজ্ঞাটা দেখায় কতটা দূরদর্শী ছিল ইউক্লিডের প্রতিভা।

একই তলে অবস্থিত দুটি সরলরেখাকে উভয়দিকে অসীমভাবে বর্ধিত করলে, যদি কোন দিকেই তারা পরস্পরকে ছেদ না করে, তাহলে এই সরলরেখাদ্বয়কে পরস্পরের সমান্তরাল বলা হয়।

এবার ফিরে যাই ইতিহাসে। পঞ্চম স্বতঃসিদ্ধর ইতিহাস। আগেই বলেছি বহু শতাব্দীর বহু গণিতজ্ঞ চেষ্টা করার পরেও কেউই এটা প্রমাণ করতে পারেন নি। শেষ পর্যন্ত, ১৮৩০ খ্রিষ্টাব্দ নাগাদ নিকোলাই লোবাচেভস্কি নামে এক রাশিয়ান গণিতজ্ঞ ও জানোস বোলেয়াই নামে এক হাঙ্গারিয়ান গণিতজ্ঞ দুজনে প্রায় একই সময়ে এই সমস্যাটার নিষ্পত্তি করলেন।^[১]

কি নিষ্পত্তি? সেটা বুঝতে আমাদের দেখতে হবে তাঁরা ঠিক কিভাবে ইউক্লিডের পঞ্চম স্বতঃসিদ্ধটা প্রমাণ করতে চেয়েছিলেন। মজার কথা হলো, পদ্ধতিটা ইউক্লিডেরই উদ্ভাবন বলে মনে করা হয় — স্ববিরোধের সাহায্যে প্রমাণ (proof by contradiction)। ব্যাপারটা এরকম:

• আমি যা প্রমাণ করতে চাইছি, তার উলটোটা সত্যি বলে ধরে নিয়ে শুরু করব।
• তারপর তার থেকে আর কি কি প্রমাণ হয়, সেটা দেখব।
• যদি এমন কিছু প্রমাণ করে ফেলি যা যৌক্তিকভাবে অসম্ভব, তাহলে আমাদের প্রথম ধরে নেওয়াটা সত্যি হতে পারে না। যেহেতু যা প্রমাণ করতে চাইছি তার উলটোটা ধরে নিয়েছিলাম, যা প্রমাণ করতে চাইছি, সেটা সত্যি হতেই হবে।

যেমন ধরা যাক, কিছু একটা বক্তব্য x-কে প্রমাণ করতে চাই। তার উলটোটা, যাকে অঙ্কের ভাষায় বলে, x কমপ্লিমেন্ট, সেটাকে সত্যি বলে ধরে নিলাম। তার থেকে ধরুন প্রমাণ করে ফেললাম, ২ < ২। যেহেতু ২ < ২ অসম্ভব, তাই প্রমাণ হয়ে গেল যে x সত্যি।

এবার পঞ্চম স্বতঃসিদ্ধের একটা তুল্যমূল্য প্রতিপাদ্য আছে। এর নাম প্লেফেয়ারের স্বতঃসিদ্ধ।

একটি সরলরেখা এবং ওই সরলরেখায় আপতিত নয় এমন একটি বিন্দু দেওয়া থাকলে, ওই বিন্দু দিয়ে ওই সরলরেখার সমান্তরাল করে একটি এবং একটিমাত্র সরলরেখা টানা যায়।

এইটা আর পঞ্চম স্বতঃসিদ্ধ যে তুল্যমূল্য, তা বোলেয়াই ও লোবাচেভস্কির অনেক আগে থেকেই জানা ছিল। কেন তুল্যমূল্য, তা আপনারাও একটু ভাবলেই বুঝতে পারবেন। পঞ্চম স্বতঃসিদ্ধ বলছে, একটি সরলরেখা অন্য দুটি সরলরেখাকে ছেদ করলে, যেদিকে অন্তর্বর্তী কোণদ্বয়ের যোগফল দুই সমকোণের কম, সেদিকে মিলিত হতে বাধ্য। তার মানে, সরলরেখা দুটি সমান্তরাল হলে, ছেদকের দুদিকেই অন্তর্বর্তী কোণদ্বয়ের যোগফলকে ঠিক দুই সমকোণ হতে হবে। আর তাই, একটি সরলরেখা ও একটি বিন্দু দেওয়া থাকলে:

• বিন্দুটা থেকে সরলরেখাটির ওপর লম্ব টানব প্রথমে।
• তারপর সেই লম্বটির উপর আর একটি লম্ব টানব বিন্দুটা দিয়ে।

এই দ্বিতীয় লম্বটিই ওই বিন্দু দিয়ে যাওয়া সমান্তরাল সরলরেখাটি, যা আমরা খুঁজছি। নিচের ছবি দেখলেই বুঝবেন ইউক্লিডীয় দ্বিসামতলীয় জ্যামিতিতে কেন এইটা হবে।

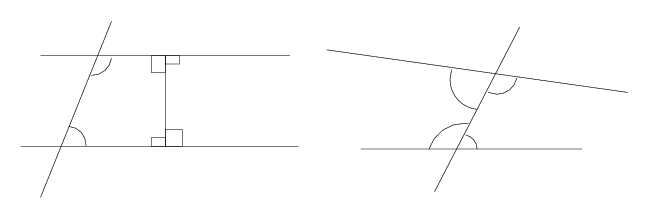
লোবাচেভস্কি ও বোলেয়াই এই তুল্যমূল্য প্রতিপাদ্যটারই উলটো ধরে নিয়ে শুরু করেছিলেন। এই প্রতিপাদ্যটার উলটো কি? যেহেতু প্রতিপাদ্যটা বলছে এক এবং একটিমাত্র সমান্তরাল সরলরেখা টানা যায় তাই তার উলটো হওয়া উচিৎ এরম:

একটি সরলরেখা এবং ওই সরলরেখায় অপতিত নয় এমন একটি বিন্দু দেওয়া থাকলে, ওই বিন্দু দিয়ে ওই সরলরেখার সমান্তরাল করে হয় একটিও সরলরেখা টানা যায় না, অথবা একাধিক সরলরেখা টানা যায়।

তা, ওঁরা দুজনেই শুরু করেছিলেন একাধিক টানা যায়, এইটা ধরে নিয়ে। উদ্দেশ্য ছিল ইউক্লিডের বাকি চারটে স্বতঃসিদ্ধ আর এই একাধিক সমান্তরাল সরলরেখা টানা যাবে, এইটা ধরে শুরু করে একের পর এক উপপাদ্য প্রমাণ করে যাবেন, যতক্ষণ না কোন যৌক্তিক স্ববিরোধ (logical contradiction) খুঁজে পান। দীর্ঘ সময় চেষ্টা করেছিলেন দুজনেই। কেউ কারও কাজের কথা জানতেনও না। মোটামুটি একই সময়ে দুজনেই থেমে যান। এবং না, দুজনের কেউই পঞ্চম স্বতঃসিদ্ধ প্রমাণ করতে পারেন নি।

তবে থেমে গেলেন কেন? কারণ দুজনেই এক আশ্চর্য কাজ করে ফেলেছিলেন। যৌক্তিক স্ববিরোধ খুঁজতে খুঁজতে তাঁরা দুজনেই একেবারে নতুন জ্যামিতি তৈরি করে ফেলেছিলেন। ইউক্লিডীয় জ্যামিতির মতই তা, আর তাতে কোন স্ববিরোধও নেই। শুধু আছে একটা কিন্তু। কিন্তু কি? তাদের তৈরি করা জ্যামিতিতে উপপাদ্যগুলো যা বলছে, সেগুলো ইউক্লিডীয় জ্যামিতির সাথে মেলে না বেশিরভাগই।

কিরকম? ধরুন, ইউক্লিডীয় জ্যামিতির একটা উপপাদ্য:

ত্রিভুজের তিনটি কোণের সমষ্টি সর্বদা দুই সমকোণের সমান।

লোবাচেভস্কি ও বোলেয়াইয়ের জ্যামিতিতে এই উপপাদ্যটা আর সত্যি নয়। তবে এরকমই একটা উপপাদ্য আছে:

ত্রিভুজের তিনটি কোণের সমষ্টি সর্বদা দুই সমকোণের কম।

এখানে মনে হতে পারে, এই তো এই একটা অসম্ভব জিনিস! এই তো পঞ্চম স্বতঃসিদ্ধ প্রমাণ হল! না, তা হল না, কারণ এটা যৌক্তিকভাবে অসম্ভব কিছু না। আমরা খাতার পাতায় ত্রিভুজ এঁকে কোণ মেপে দেখলে দুই সমকোণ বেরোয় ঠিক, তাই এই উপপাদ্যটা অদ্ভুত হতে পারে। কিন্তু ২ < ২, এটা যেমন যৌক্তিকভাবে অসম্ভব (logical impossibility), অর্থাৎ কোন নির্ভুল যুক্তিতেই অমন একটি প্রতিপাদ্য সত্যি হতে পারে না, তেমন কিছু নয়।

কিন্তু আমাদের রোজকার অভিজ্ঞতার সাথে ওনাদের জ্যামিতির এরকম বহু উপপাদ্যই মিলছিল না। সে এক আশ্চর্য নতুন জগৎ! এতটাই আলাদা জ্যামিতি আবিষ্কার করেছিলেন তাঁরা যে ঠিক কি ঘটেছে সেটা বুঝে উঠতে খানিক সময় লেগেছিল। ১৮৪৮ সাল থেকে গণিতজ্ঞরা এই নিয়ে ভীষণভাবে মাথা ঘামাতে শুরু করেন। এক সময় ফেলিক্স ক্লেইন প্রমাণ করলেন যে, এই জ্যামিতিগুলি যৌক্তিকভাবে স্ববিরোধমুক্ত যদি এবং কেবলমাত্র যদি ইউক্লিডীয় জ্যামিতি যৌক্তিকভাবে স্ববিরোধমুক্ত হয়।

সমস্তটা বুঝে উঠতে ইতিহাসকে আরো অপেক্ষা করতে হয়েছিল, রীমানের প্রতিভার জন্য। ওনারা যে জ্যামিতিগুলো আবিষ্কার করেছিলেন সেগুলোকে বলে অধিবৃত্তীয় জ্যামিতি (hyperbolic geometry)। পরে, ইউক্লিডীয় জ্যামিতির থেকে আলাদা কিন্তু এগুলোর থেকে অন্যরকম আরও জ্যামিতি আবিষ্কার হয়, সেগুলোকে বলা হয় উপবৃত্তীয় জ্যামিতি (elliptic geometry)। আর ইউক্লিডীয় জ্যামিতির থেকে আলাদা এই সমস্ত জ্যামিতিগুলোকে একসাথে বলা হয় অনিউক্লিডীয় জ্যামিতি (non euclidean geometry)।

পরের অংশে আমরা দেখব এই জ্যামিতিগুলো কেন এমন অদ্ভুত আর এরা কিই বা বলছে।

[১] বোলেয়াই তাঁর আবিষ্কারের কথা যখন গাউস (Karl Frederick Gauss) কে জানান, ততদিনে গাউস নিজেও এই আবিষ্কার করেছিলেন। যদিও এ নিয়ে তাঁর কোন কাজ কখনো প্রকাশিত হয়নি।

লেখাটি অনলাইন পড়তে হলে নিচের কোডটি স্ক্যান করো।

Scan the above code to read the post online.

Link: https://bigyan.org.in/elements-of-geometry-part-3

print