14-05-2025 07:16:54 am

বিজ্ঞান - Bigyan

বাংলা ভাষায় বিজ্ঞান জনপ্রিয়করণের এক বৈদ্যুতিন মাধ্যম
An online Bengali Popular Science magazine

https://bigyan.org.in

ব্রাকিস্টোক্রোন সমস্যা: সমাধান ও প্রয়োগ

অনির্বাণ ঘোষ

("বিজ্ঞান" সম্পাদক)

প্রদীপ্ত পঞ্চাধ্যায়ী

(কাঁথি প্রভাত কুমার কলেজ)

অভিজিৎ কর গুপ্ত

(পাঁশকুড়া বনমালী কলেজ)

03 Apr 2024

Link: https://bigyan.org.in/brachistochrone-curve-02

%e0%a6%ac%e0%a7%8d%e0%a6%b0%e0%a6%be%e0%a6%95%e0%a6%bf%e0%a6%b8%e0%a7%8d%e0%a6%9f%e0%a7%8b%e0%a6%95%e0%a7%8d%e0%a6%b0%e0%a7%8b%e0%a6%a8-%e0%a6%b8%e0%a6%ae%e0%a6%b8%e0%a7%8d%e0%a6%af%e0%a6%be

আগের পর্বে আমরা দেখেছি, গণিতজ্ঞ বার্নোলি “ব্রাকিস্টোক্রোন” সমস্যা সমাধানের চ্যালেঞ্জ ছুঁড়লেন ইউরোপের বাঘা বাঘা গণিতজ্ঞদের দিকে। সমস্যাটা হলো: একটা নুড়ি যদি উঁচু থেকে একটা খাঁজকাটা পথে নামে, খাঁজটা কীভাবে কাটলে সবথেকে কম সময় লাগবে। সবচেয়ে চমকপ্রদ সমাধানটা কিন্তু দিলেন বার্নোলি নিজেই। তিনি দেখালেন, একটা নুড়ি যে পথে সবথেকে দ্রুত নেমে আসবে সেটা বের করার অঙ্ক আসলে আলোর প্রতিসরণের পথ বের করার অঙ্কের সমতুল্য। আলোর প্রতিসরণের সূত্র আগেই জানা ছিল। ব্রাকিস্টোক্রোন সমস্যায় সেই সূত্র কাজে লাগাতেই বেরিয়ে এলো বার্নোলির আশ্চর্য সমাধান।

ফার্মার নীতি ও স্নেলের সূত্র

ব্রাকিস্টোক্রোন প্রবলেমের সমাধান করতে গিয়ে বার্নোলি অদ্ভুতভাবে কাজে লাগিয়েছিলেন আলোকবিদ্যার কিছু প্রাথমিক নিয়ম। তোমরা নিশ্চয়ই জানো, আলোক রশ্মি এক বিন্দু থেকে অন্য কোনো বিন্দুতে যেতে গেলে এমন পথ অনুসরণ করে যাতে সবচেয়ে কম সময় লাগে। এটা আসলে বিখ্যাত গণিতজ্ঞ ফার্মার নীতি (Fermat’s principle)।

এছাড়া, আলোর এক মাধ্যম থেকে অন্য মাধ্যমে প্রতিসরণ ঘটার ক্ষেত্রে বিখ্যাত সেই স্নেলের সূত্রের কথাও তোমরা সবাই পড়েছো। ধরি, প্রথম মাধ্যম থেকে কোনো নির্দিষ্ট তরঙ্গদৈর্ঘ্যের আলো দ্বিতীয় মাধ্যমে যাচ্ছে। প্রথম মাধ্যমে আলোর আপতন কোণ $\theta_1$ ও দ্বিতীয় মাধ্যমে আলোর প্রতিসরণ কোণ $\theta_2$ হলে স্নেলের সূত্র বলে:

$\frac{sin\theta_1}{v_1} = \frac{sin\theta_2}{v_2}$

যেখানে $v_1$ ও $v_2$ হল প্রথম ও দ্বিতীয় ও মাধ্যমে আলোর গতিবেগ।

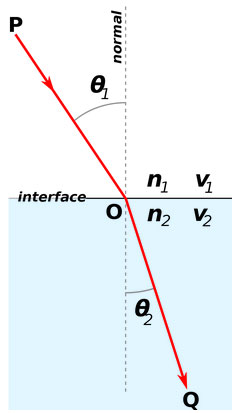
জ্যামিতির অঙ্ক কষে দেখানো যায় যে প্রতিসরণের ক্ষেত্রে ফার্মার নীতি আর স্নেলের সূত্র এক্কেবারে সমতুল্য। অর্থাৎ যে পথ স্নেলের সূত্র মেনে চলে সেই পথেই আলোর যেতে সবচেয়ে কম সময় লাগে!

মজার ব্যাপার হলো এই দুই সূত্রের সমতুল্যতা একটা নিছকই জ্যামিতিক উপপাদ্য। অর্থাৎ এটা প্রমাণ করতে শুধু এটুকুই ধরতে হয় যে, কোনো একটা বস্তু $v_1$ গতিসম্পন্ন মাধ্যম থেকে $v_2$ গতিসম্পন্ন মাধ্যমে যাচ্ছে। বস্তুটা ঠিক কী তা অপ্রাসঙ্গিক। তা আলোও হতে পারে, আবার একটা ভরযুক্ত কণাও হতে পারে!

নিরন্তরভাবে পরিবর্তনশীল মাধ্যম

স্নেলের সূত্রকে একটু অন্যভাবে বলা যায়। যখন আলো অনেকগুলি মাধ্যম দিয়ে যায়, যার প্রতিটিতে তার গতিবেগ আলাদা, তখন তার গতিপথের উপর সর্বত্র $\frac{sin\theta}{v}$ মানটি ধ্রুবক (constant)। অর্থাৎ একটি বিশেষ পথের ওপর যে বিন্দুতেই এই মানটি নির্ণয় করা হোক না কেন সর্বদা একই উত্তর পাওয়া যাবে। এখানে হলো সেই বিন্দুতে উল্লম্বরেখা আর পথটির মধ্যবর্তী কোণ। আর $v$ হলো সেই বিন্দুতে আলোর গতিবেগ।

এবার ভাবো আলো এমন একটা মাধ্যম দিয়ে যাচ্ছে যাতে তার গতিবেগ মাধ্যমের গভীরতা $y$ -এর সাথে সাথে নিরন্তরভাবে পরিবর্তিত হচ্ছে কোনো একটা অপেক্ষক $v(y)$ অনুযায়ী। এক্ষেত্রে ভাবা যায় মাধ্যমটি আসলে পরপর অনেকগুলি ছোট ছোট স্তর দিয়ে তৈরি।

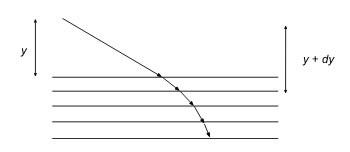
এদের একেকটির গভীরতা এতো সামান্য যে শূন্যের কাছাকাছি ধরা যায়। আর $y$ এবং $y + dy$ গভীরতার মাঝে যে স্তরটি আছে সেখানে আলোর গতিবেগ $v(y)$ । অর্থাৎ মাধ্যমের প্রতি স্তরে ঐ খুব ছোট ছোট গভীরতা অতিক্রম করার সাথে সাথে আলোর বেগের সামান্য সামান্য পরিবর্তন হচ্ছে।

এইরকম নিরন্তর প্রতিসরণ হলে আলোর পথ আগের মতো অনেকগুলো সরলরেখাংশের সমষ্টি না হয়ে একটা একটানা বক্ররেখা হবে। কিন্তু আমরা স্নেলের সূত্রকে উপরে যে একটু অন্যভাবে লিখলাম, সেটা কিন্তু এক্ষেত্রেও সোজাসুজি প্রয়োগ করা যাবে:

$\frac{sin\theta(y)}{v(y)} = k$

এখানে $k$ একটি ধ্রুবক অর্থাৎ তার মান $y$ -এর ওপর নির্ভরশীল নয়। আর $\theta(y)$ হলো $y$ গভীরতায় আলোর পথের স্পর্শক আর উল্লম্বরেখার মধ্যে কোণ।

এটা কিন্তু একটা দারুণ সমীকরণ! যেহেতু $v(y)$ দেওয়া আছে, $k$ -এর কোনো একটা বিশেষ মানের জন্যে $\theta(y)$ অপেক্ষকটা আমরা পুরোপুরি জেনে গেলাম:

$\theta(y) = sin^{-1}(k\cdot v(y))$

এবার কোনো একটা বিন্দু $(x_0, y_0)$ থেকে শুরু করে আলোর পুরো পথটাই এঁকে ফেলা যাবে। কারণ প্রতিটি বিন্দুতে পথটা ঠিক কোন কোণে হেলে আছে সেটা এই সমীকরণ থেকে জানা যাচ্ছে। যেমন, শুরুর বিন্দু থেকে যদি আমি পথ বরাবর $X$ -দিকে একটুখানি $dx$ এগোই, তাহলে $Y$ -দিকে আমি ঠিক যতটা $dy$ নামবো সেটা হবে $dy = cot\theta(y_0)dx$ । সুতরাং, আমি শুরুর বিন্দু থেকে পথের ওপর একটুখানি এগিয়ে গেলাম। এবার এই নতুন বিন্দু থেকে তার পাশের বিন্দুটা কী হবে একইভাবে নির্ণয় করতে পারবো। এইভাবে এগোতে থাকলে আস্তে আস্তে পুরো পথটাই এঁকে ফেলা যাবে।

এখানে বলে রাখি, এইভাবে একটু একটু করে এগিয়ে চলার ব্যাপারটা সহজেই কম্পিউটারে প্রোগ্রাম লিখে করে ফেলা যায়। কিছু বিশেষ $v(y)$ -এর জন্যে কাগজে কলমে ইন্টিগ্রেশন কষেও পথটা বের করা যায় — কিন্তু বেশিরভাগ $v(y)$ -এর জন্যই যায় না।

বার্নোলির সমাধান

লেখার শুরুতে আমরা যে স্নেলের সূত্র আর ফার্মার নীতির সমতুল্যতার কথা বলেছিলাম সেটা ভাবো। মনে রাখো যে এই সমতুল্যতা শুধু আলো নয়, বস্তুকণার ক্ষেত্রেও খাটে।

আমাদের নতুনভাবে লেখা স্নেলের সূত্রের ক্ষেত্রে সেই সমতুল্যতার নীতি প্রয়োগ করে আমরা এই সিদ্ধান্তে আসতে পারি:

ধরি, একটি বস্তুকণা একটি দ্বিমাত্রিক $XY$ তলে অবস্থিত, $A$ বিন্দু থেকে $B$ বিন্দুতে যাচ্ছে। সে এমনভাবে চলেছে যে তার গতিবেগ পরিবর্তিত হচ্ছে $v(y)$ অপেক্ষক অনুযায়ী। এই অপেক্ষকটা আগে থেকে বলে দেওয়া আছে, কিন্তু বস্তুটার পথের জ্যামিতিক আকার যা খুশি হতে পারে। সমস্ত আকারের পথের মধ্যে সেই পথে যেতে বস্তুটার সবচেয়ে কম সময় লাগবে যেটা এই সমীকরণ মেনে চলে:

$\frac{sin\theta(y)}{v(y)} = k$

এইবার ফিরে আসি ব্রাকিস্টোক্রোন সমস্যায়। ধরো, একটা $m$ ভরের কণা স্থিতাবস্থা থেকে ঘর্ষণহীন পথে নামছে। শুরুর বিন্দু থেকে উল্লম্বভাবে $y$ দূরত্ব নেমে এলে তার গতিবেগ কী হবে তা আমরা যান্ত্রিক শক্তির সংরক্ষণ সূত্র কাজে লাগিয়ে বলতেই পারি:

$\frac{1}{2}mv^2 = mgy$

যেখানে $g$ হল অভিকর্ষজ ত্বরণ। তাহলে,

$v(y) = \sqrt{2gy}$

দেখতেই পাচ্ছো এই গতিবেগ শুধু পতনের ‘গভীরতা’ $y$ -এর ওপর নির্ভরশীল, ঠিক আমাদের উপরের প্রতিপাদ্যের শর্তের মতো। বিশেষ করে, পথটির জ্যামিতিক আকৃতির ওপর এই $v(y)$ নির্ভর করে না।

তাহলে আমাদের উপরের প্রতিপাদ্য প্রয়োগ করে পাই, যে পথে কণাটির নামতে সবচেয়ে কম সময় লাগবে সেই পথ এই সমীকরণ মানবে:

$\frac{sin\theta(y)}{\sqrt{y}} = k$

মাধ্যমে আলোর গতিবেগ নিরন্তরভাবে পরিবর্তিত হলে আলোর গতিপথে স্নেলের সূত্রের প্রয়োগ (Credit — 3Blue1Brown)

আমরা আগেই দেখেছি এই সমীকরণ থেকে পথটার চেহারা নির্ণয় করার মূল নীতি কী। এই বিশেষ সমীকরণটার সমাধান করতে কম্পিউটার লাগে না— কাগজে কলমে ইন্টেগ্রেশনের অঙ্ক কষেই বের করা যায়। আমরা সেই অঙ্কের খুটিঁনাটিতে যাবো না। শুধু এইটুকুই বলি যে, এই সমীকরণের সমাধান করে জোহান বার্নোলি দেখিয়েছিলেন এই গোটা পথটা একটা সাইক্লয়েড আকারের হবে। সুতরাং, প্রমাণিত হলো যে ব্রাকিস্টোক্রোন একটা সাইক্লয়েড।

বার্নোলির সমাধানের সীমাবদ্ধতা

বার্নোলির এই সমাধান যেন পদার্থবিদ্যা ও অঙ্কের অপূর্ব এক মেলবন্ধন! তবে, গণিতজ্ঞরা সবাই তা পুরোপুরি পছন্দ করলেন না। এইরকম প্রমাণ যদিও খুবই সুন্দর, তবুও এই পদ্ধতি অন্য কোনো প্রবলেমের ক্ষেত্রে প্রয়োগ করা যাবে না। কারণ এই পদ্ধতিটা পুরোপুরি নির্ভর করে ব্রাকিস্টোক্রোন সমস্যার সাথে নিরন্তরভাবে পরিবর্তনশীল মাধ্যমে আলোর প্রতিসরণের সমস্যার মিলের ওপর। এই মিলটা খুঁজে পাওয়া অবশ্যই জোহান বার্নোলির অসাধারণ বুদ্ধির পরিচয়, কিন্তু তবুও এটা একটা প্রায় কাকতালীয় মিলের বেশি কিছু না।

আমরা আগের পর্বে দেখেছি যে, ব্রাকিস্টোক্রোন সমস্যা আসলে “অপেক্ষকের অপেক্ষক”-এর মিনিমাম বা ম্যাক্সিমাম বের করার সাধারণ সমস্যার একটা বিশেষ উদাহরণ। এই সাধারণ সমস্যাটার সমাধানের একটা উপায় যদি বের করা যেত তাহলে দারুণ হতো। কারণ সেই উপায়ে ব্রাকিস্টোক্রোনের মতো আরও হাজারটা সমস্যার সমাধান করা যেত। আমরা এও বলেছি যে সেই পদ্ধতি বার করেছিলেন জোহান বার্নোলির পরবর্তী প্রজন্মের গণিতজ্ঞরা — জোহান বার্নোলির ছাত্র লিওনার্ড অয়লার এবং প্রতিভাবান ফরাসী গণিতজ্ঞ জোশেফ ল্যুই লাগ্রাঞ্জ। তাঁদের সেই সমাধান অয়লার-লাগ্রাঞ্জ সমীকরণ নামে খ্যাত।

আমরা আজকের লেখায় অয়লার-লাগ্রাঞ্জ সমীকরণের তত্ত্বে যাবো না। শুধু ব্রাকিস্টোক্রোন প্রবলেমের বাইরে গণিত ও পদার্থবিদ্যায় এই তত্ত্বের ব্যাপক প্রয়োগের কয়েকটা উদাহরণ দিয়ে আমাদের আলোচনা শেষ করবো। কিন্তু তার আগে একটা হাতে কলমে পরীক্ষার কথা ছোট্ট করে বলে নিই।

হাতে কলমে বানাও: ল্যাবে ব্রাকিস্টোক্রোন

আচ্ছা এতক্ষণ তত্ত্বের কচকচির মধ্যে কাটিয়ে নিশ্চয় নিজের চোখে দেখতে ইচ্ছে করছে কীভাবে ব্রাকিস্টোক্রোন পথে নুড়ি সবচেয়ে চটপট নেমে আসে? কয়েকটা উপকরণ হাতের কাছে থাকলে ব্রাকিস্টোক্রোন প্রবলেমের উপর তোমরা নিজেরা মডেল বানিয়ে ফেলতে পারো। তারপর অনেকগুলো বল একসাথে উপর থেকে ছেড়ে দেখতে পারো কোন বল আগে পৌঁছায়। মডেল বানানোর বিশদ বিবরণ পাবে এই ওয়েবসাইটে।

ব্রাকিস্টোক্রোন প্রবলেম হাতে নাতে যাচাই করে দেখার এক মডেল (Credit — Autodesk Instructables)

আরও আরও সমস্যা: নতুন ক্যালকুলাসের ক্ষমতা

গ্যালিলিওর শেষ বইতেই ব্রাকিস্টোক্রোন সমস্যা ছাড়া ছিল আরেকটা প্রবলেম, একটা অতি সাধারণ বিষয়। ধরা যাক, দুটো বিদ্যুতের খুঁটির মাঝখানে ঝুলে আছে একটা ভারী ইলেক্ট্রিক তার। এই ঝুলন্ত তারের আকার কীরকম হবে? তা কি অধিবৃত্তাকার (parabola)?

গ্যালিলিওর গণনা অনুযায়ী তা হবে অধিবৃত্ত। তবে, অয়লার-ল্যাগ্রাঞ্জ সমীকরণ দিয়ে হিসাব করে দেখা গেল তার প্রকৃত গাণিতিক রূপ হবে নতুন রকম কিছু। তাকে বলা হলো ক্যাটিনারি (catenary)। এই ক্যাটিনারি শব্দটা এসেছে ল্যাটিন শব্দ ক্যাটিনা থেকে, যার অর্থ শিকল বা চেইন। ঝুলন্ত কোনো চেইন-এর ওই আকারকে বলা হলো ক্যাটিনারি।

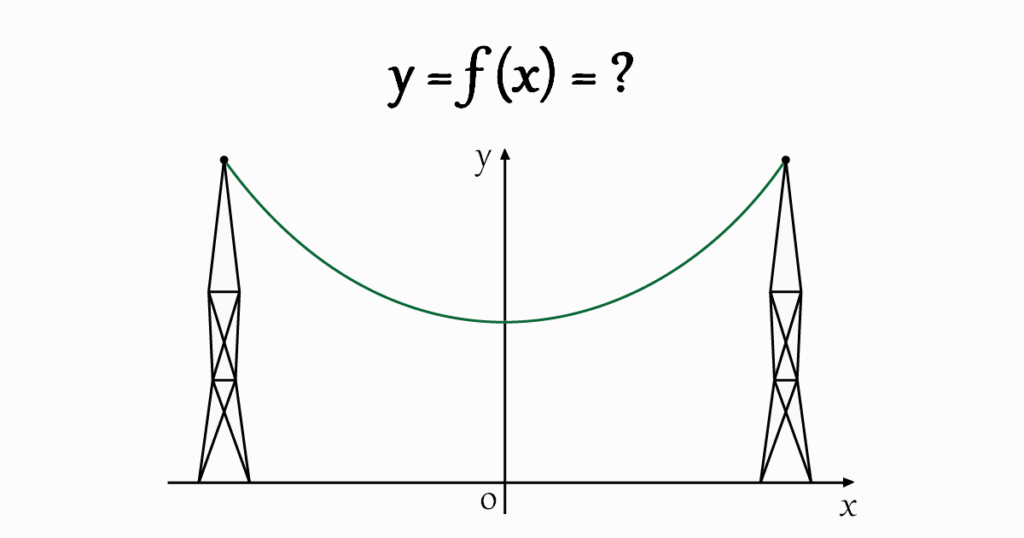
ঝুলন্ত ওজনদার চেইন-এ ক্যাটিনারি বক্রের রূপ (Credit — Art of mathematics)।

ভারী সুন্দর এই ভ্যারিয়েশনাল ক্যালকুলাস-এর ভাবনাটা। অয়লার-ল্যাগ্রাঞ্জ সমীকরণ দিয়ে কত অনায়াসে যে ইন্টারেস্টিং সব প্রবলেমের সমাধান করে ফেলা যায় তা ভাবাই যায় না। ধরা যাক, দুটো রিং-কে সাবান জলে চুবিয়ে তুলে নিয়ে ধীরে ধীরে তাদের আলাদা করা হচ্ছে। দেখা যাবে তাদের মধ্যে একটা সাবানের ফিল্ম (soap film) তৈরি হচ্ছে। প্রশ্ন হলো, এই ফিল্মের আকার কীরকম হবে? একটা জিনিস ভাবতে হবে, এই ফিল্মের আকার এমন হবে যাতে তার ক্ষেত্রফল মিনিমাম হয়, যাকে বলা হয় ‘মিনিমাম এনার্জি সারফেস’। কেননা, পৃষ্ঠটান (surface tension) -এর কারণে একটা সাবানের ফিল্মের মধ্যে জমা থাকা স্থিতিশক্তি তার ক্ষেত্রফলের সমানুপাতিক এবং প্রকৃতি ন্যূনতম শক্তির অবস্থাই পছন্দ করে।

ধরা যাক, একটা অনুভূমিক লাইন (x-axis), তার একদিকে দুটো বিন্দু, তাদের যোগ করে একটা বক্ররেখা টানা হলো। এবার কল্পনা করো, এই বক্রকে এই অনুভূমিক লাইন বা অক্ষের চারপাশে ঘুরিয়ে একটা তল তৈরি করা হচ্ছে।

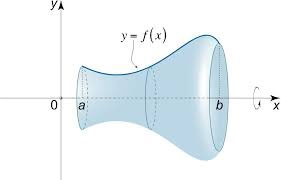
বক্রকে অনুভূমিক অক্ষের চারপাশে ঘুরিয়ে একটা তল তৈরি করা হচ্ছে (Credit — Math24)

তাহলে, এই বক্রের চেহারা কীরকম হতে হবে যাতে সেই তলের পৃষ্ঠের ক্ষেত্রফল হয় সবচেয়ে কম? আসলে, এটাই তো সাবানের ফিল্ম! অয়লার-ল্যাগ্রাঞ্জ সমীকরণ তথা ভ্যারিয়েশানাল ক্যালকুলাসের-এর সাহায্যে হিসাব করে দেখা যাচ্ছে এই বক্রের আকার হবে একটা ক্যাটিনারি!

সেদিন এই অঙ্কটা নিয়েই আলোচনা করছিলাম ক্লাসে। শেষ পর্যন্ত পুরো অঙ্কটা হাতে কষে বার করা যায় না। কম্পিউটারের সাহায্য নিতে হয়। কম্পিউটারের সাহায্যে একটা প্যারামিটারের মান বার করতে গিয়ে দেখা গেল তার দু-রকম মান আসছে। অর্থাৎ, কম্পিউটারের হিসাব বলছে, দু-রকম পৃষ্ঠতল হতে পারে — বেশি গভীর এবং অল্প গভীর পৃষ্ঠতল (deep and flat surface)! সেক্ষেত্রে, বক্রের চেহারা হতে পারে গভীর বক্রতা সম্পন্ন অথবা কম বক্রতা সম্পন্ন ক্যাটিনারি।

ছবিটবি এঁকে বোঝানোর সময় এক ছাত্র প্রশ্ন করল, সেটা কী করে হয়? সাবানের ফিল্মের দু-রকম সারফেস কেন হবে? প্রকৃতি তো সেই সারফেসই তৈরি করবে যার ক্ষেত্রফল ন্যূনতম। আসলে, তাই হয়। দুটো কেসের মধ্যে যার ক্ষেত্রফল ন্যূনতম (অগভীর পৃষ্ঠতল) সেটাই আসলে দেখা যায় বাস্তবে।

পরে তথ্য ঘেঁটে জানা গেল এসব নিয়ে প্রচুর স্টাডি হয়েছে সে যুগে! প্ল্যাটো (Joseph Plateau, 1801 – 83), বয়েস (C.V. Boys, 1855-1945) এঁরা দীর্ঘদিন পরীক্ষা-নিরীক্ষা করেছেন সাবানের ফিল্ম নিয়ে। আসলে, সাবান ফিল্মের স্টাডি, সাবান বুদ্বুদের জোড়া লাগা, এদের সীমানা (boundary), ন্যূনতম ক্ষেত্রফলযুক্ত পৃষ্ঠতল (minimum surface) তৈরি — এসবই ভীষণ গুরুত্বপূর্ণ বিষয়। কোথায় না এগুলোর ধারণা কাজে লাগে — জীববিদ্যার বিভিন্নরকম প্রবলেম বোঝার ক্ষেত্রে, জ্যোতির্পদার্থবিদ্যা (Astrophysics) বা মহাবিশ্বতত্ত্ব (Cosmology)-এর নানান ভাবনায় ও মডেল তৈরি করে বোঝার ক্ষেত্রে। এবং অবশ্যই গণিতজ্ঞদের মধ্যে যাঁরা টপোলজি নিয়ে কাজ করেন তাঁরা ন্যূনতম ক্ষেত্রফলযুক্ত পৃষ্ঠতল নিয়ে বিবিধ গবেষণা করেন।

সাবানের ফিল্ম এ গোল্ডস্মিথ সলিউশান (Credit — Cambridge University)

সাবানের বুদ্বুদ নিয়ে আমাদের এই পরীক্ষাতে আরেকটা জিনিস দেখা যায়। দুটো রিং-এর মধ্যে দূর‍ত্ব বাড়াতে থাকলে একসময় ফিল্মটা ভেঙে গিয়ে দু-দিকের দুটো রিং-এ দুটো গোলাকার পৃষ্ঠতল তৈরি হয়ে যায়। অঙ্ক কষে এবং কম্পিউটারের সাহায্যেও এইরকম সিদ্ধান্তই করা যায়। এই যে হঠাৎ করে একটা পরিবর্তন দেখা যায়, একে বলে গোল্ডস্মিথ সলিউশান। গোল্ডস্মিথ (C.W.B. Goldschmidt, 1807 – 51) এই ব্যাপারটা নিয়ে চমৎকার অঙ্ক কষে দেখান 1831 সালে। তবে, আমরা হয়তো আগে তাঁর নাম বিশেষ শুনি নি। গোল্ডস্মিথ সেরকম বিখ্যাত কেউ না হলেও তিনি ছিলেন বিখ্যাত গটিনগেন (Göttingen) ইউনিভার্সিটি-তে এস্ট্রনমির অধ্যাপক। এছাড়া, তিনি ছিলেন সেখানকার অবজারভেটরি-তে স্বনামধন্য গণিতজ্ঞ কার্ল ফ্রেইড্রিখ গাউসের সহকারি। এই যে একটা বক্ররেখাকে ঘুরিয়ে ন্যূনতম ক্ষেত্রফলযুক্ত পৃষ্ঠতল তৈরি করার অঙ্ক, এসব এখন প্রায় সব বইতেই থাকে। এটা নি:সন্দেহে গোল্ডস্মিথের অবদান। তবে, গোল্ডস্মিথ সম্পর্কে বিশেষ কিছুই লেখা থাকে না অঙ্কের বইগুলোতে।

একটা অসাধারণ বই পড়ছিলাম— Paul J. Nahin-এর লেখা “When Least is Best”! এই লেখার অধিকাংশ তথ্যই এই বই থেকে নেওয়া। ভাবছিলাম, ন্যূনতম ক্ষেত্রফলযুক্ত পৃষ্ঠতল কিংবা ন্যূনতম সময়ের পথ এরকম সব অতি সাধারণ অথচ কত গুরুত্বপূর্ণ প্রবলেম গ্যালিলিওর হাত ঘুরে, আরো কত শত গণিতজ্ঞ ও পদার্থবিদের হাতের ছোঁয়ায় এখন নিশ্চিন্তে স্থান করে নিয়েছে আমাদের সভ্যতার টেক্সট বইতে! আর, বিজ্ঞান ও অঙ্কের জগতে এসেছে কতই না পরিবর্তন!

(প্রচ্ছদের ছবির সূত্র)

===================

সহযোগী পাঠ ও দেখার জন্য: