এর আগের পর্বে আমরা দেখেছিলাম তাত্ত্বিক কম্পিউটার সায়েন্স-এ কী ধরণের সমস্যা নিয়ে ভাবা হয়। বিশেষ করে জেনেছিলাম জটিলতার তত্ত্ব বা কমপ্লেক্সিটি থিওরি-র (complexity theory) কথা। এই পর্বে আমরা আরেক ধাপ এগিয়ে এই ধরণের গবেষণার কিছু নমুনা দেখবো।
সৌমিকঃ আপনার গবেষণা কোয়ান্টাম কমপ্লেক্সিটি থিওরি (জটিলতার তত্ত্ব) এবং কোয়ান্টাম ইনফরমেশন এই দুদিকেই বিস্তৃত। এই দুটি বিষয়ের মধ্যে সম্পর্ক নিয়ে যদি কিছু বলেন।
জনঃ কোয়ান্টাম জগতে জটিলতার কথা বলতে হলে আগে কোয়ান্টাম জগতের তথ্যকে অঙ্কের ভাষায় প্রকাশ করতে হবে, যেটা কোয়ান্টাম ইনফরমেশন করে। এটাই কোয়ান্টাম কমপ্লেক্সিটি থিওরির মজা; আমরা একটা কোয়ান্টাম মেশিন দিয়ে একটা সমস্যা সমাধান করা কতটা সোজা বা শক্ত – সেটা বুঝতে চাই। কিন্তু অনেকসময়, সেটা বুঝতে গিয়ে কোয়ান্টাম তথ্য নিয়েই কিছু মৌলিক প্রশ্নের সম্মুখীন হতে হয়। এই প্রশ্নগুলোর সাথে কোয়ান্টাম জগতে জটিলতার তত্ত্বের হয়ত বিশেষ সম্পর্ক নেই, সেগুলো হয়ত পুরোপুরি অঙ্কের কিছু প্রশ্ন – যেমন কোনও matrix এর কিছু বৈশিষ্ট্য।
অন্যভাবে বললে, জটিলতার তত্ত্ব নিয়ে প্রশ্নের উত্তর পেতে গেলে আগে অঙ্কের কিছু জটিল ধাঁধার উত্তর খুঁজতে হয়। অনেক সময়ই ধাঁধাগুলো খুবই জটিল, কীভাবে সমাধান করবো, আমাদের জানা নেই। কিন্তু অনেক সময় জানা থাকে, আর অঙ্কের প্রশ্নটা সমাধান করতে পারলেই মূল জটিলতা নিয়ে প্রশ্নটারও সমাধান হয়ে যায়। এভাবে খুব গুরুত্বপূর্ণ কিছু প্রশ্ন পাওয়া গেছে – যাদের প্রয়োগ জটিলতার তত্ত্বের বাইরে সম্পূর্ণ ভিন্ন কোনো জায়গায়।
রাজীবুলঃ বিভিন্ন জিনিসের পারস্পরিক সম্পর্ক বলতে মনে পড়লো, কমপ্লেক্সিটি ক্লাস (জটিলতার শ্রেণী) বলে একটা কথা হয়, তাই না? এই কমপ্লেক্সিটি ক্লাস ঠিক কী? কোয়ান্টামেও যেতে হবে না, একটা কমপ্লেক্সিটি ক্লাসের সনাতন সংজ্ঞাটাই বা কী?
জনঃ কমপ্লেক্সিটি ক্লাস হলো কিছু গাণিতিক সমস্যার সেট বা সমষ্টি – একদম সেট থিওরির সেটের মত, ব্যাস এইটুকুই। আমরা যা ইচ্ছে কিম্ভূত সেট বানাতেই পারি – এমন কিছু গাণিতিক সমস্যা একত্রিত করলাম যেগুলোর মধ্যে পারস্পরিক কোনও সম্পর্কই নেই। কিন্তু সাধারণত আমরা সেটা করি না। যেটা করি সেটা হলো – এমন কিছু সেট বানাই যার মধ্যে কিছু পারস্পরিক সম্পর্কযুক্ত গাণিতিক সমস্যা আছে, যে সম্পর্কটা কোনো না কোনো কারণে মৌলিক বা কৌতুহলোদ্দীপক [১]; যেমন হয়তো সেটে অন্তর্ভুক্ত সবকটা সমস্যা কোনও একটা নির্দিষ্ট কম্পিউটার দিয়ে কোনও একটা নির্দিষ্ট মডেলের সাহায্যে একটা নির্দিষ্ট সময় বা অন্য কোনো সীমার মধ্যে সমাধান করা যাবে।
রাজীবুলঃ ধরা যাক, একটা কমপ্লেক্সিটি ক্লাস নিয়ে চর্চা হচ্ছে, এবং একটা যন্ত্র বানানো হয়েছে বা পদ্ধতি পাওয়া গেছে যা ওই ক্লাসের একটা সমস্যার সমাধান করতে পারে। এটা কি বলা যায় যে ওই ক্লাসের বাকি সমস্যাগুলোও নিশ্চিতভাবেই সমাধান করা যাবে?
জনঃ এটা তখনি সম্ভব যখন আমরা সেই ক্লাস-টার কোনও একটা যাকে বলে “complete” (পূর্ণ) সমস্যার সমাধান করতে পারি। কিন্তু সেই ক্লাস-টার যেকোনো একটা সমস্যা সমাধান করলেই যে বাকিগুলো পারা যাবে এমনটা নয়। ধরুন আমি সেইসব গাণিতিক সমস্যাকে একত্রিত করলাম যেগুলো একটা সাধারণ কম্পিউটার নির্দিষ্ট সময়ের মধ্যে সমাধান করতে পারে। এই ক্লাস-টায় অনেক শক্ত শক্ত সমস্যা থাকতে পারে, আবার খুব সহজ ও খুব তুচ্ছ কিছু সমস্যাও থাকতে পারে – যেমন ধরুন একটা সমস্যা যেখানে উত্তর সবসময় ০, যে ইনপুটই দেওয়া হোক না কেন। এটা আমরা খুবই সহজে সমাধান করতে পারি – কম্পিউটারকে সবসময় ০ আউটপুট দিতে বলব, তাহলেই হলো। কিন্তু এত সোজা একটা সমস্যার সমাধান করছি মানেই এই ক্লাসটার শক্ত শক্ত সমস্যাগুলোর সমাধান করে ফেলব, এমনটা নয়।
কিন্তু ধরা যাক আমরা কমপ্লেক্সিটি ক্লাসটার “সবচেয়ে শক্ত” সমস্যাটার সমাধান করে ফেলেছি; ‘complete’ সমস্যা বলতে অনেকটা সেটাই বলা হচ্ছে – এমন একটা প্রবলেম্ যেটা সমাধান করলে ক্লাসটার বাকি সব সমস্যার সমাধান করা যাবে। প্রায় সব গুরুত্বপূর্ণ কমপ্লেক্সিটি ক্লাস-এর এরম “complete” সমস্যা আছে। কিন্তু কয়েকটা ক্লাস-এর আবার নেই বা পাওয়া যায়নি। সেই ক্লাসগুলি বেশ অদ্ভুত – হবে নাই বা কেন, মাঝেমাঝে কমপ্লেক্সিটি ক্লাস ব্যাপারটা খানিকটা অদ্ভুতুড়েই বটে!
রাজীবুলঃ জটিলতা তত্ত্বের এমন কিছু সমস্যার কথা বলুন যা আপনার মনে হয় পরের ১০ বছরে কেউ না কেউ সমাধান করে ফেলবে। মানে ধরুন একদম গরম জিলিপির মত কিছু প্রবলেম্।
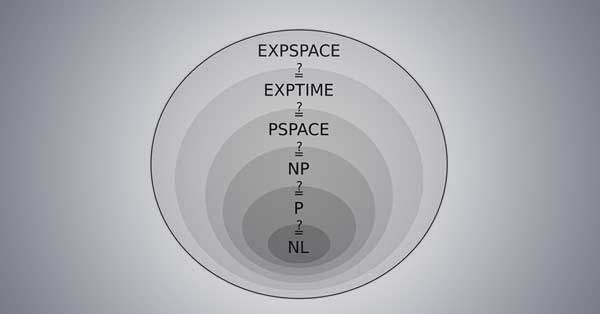
জনঃ অনেক এরকম সমস্যা আছে। আমরা কমপ্লেক্সিটি ক্লাসগুলো কোনটা কার চেয়ে কত বেশি বড় সেটা একদমই ভালো বুঝিনা। যেমন ধরুন P আর PSPACE। P মানে যেসব সমস্যা polynomial সময়ে সমাধান করা যাবে, আর PSPACE মানে যেসব প্রবলেম্ polynomial স্পেসে সমাধান করা যাবে। P অবধারিত ভাবে PSPACE-এর সাবসেট – polynomial সময়ে কোনও algorithm-এর polynomial-এর বেশি স্পেস লাগতে পারে না [২, ৩]। তবে সাবসেট-টা প্রপার কিনা আমরা জানি না।
এটা ভাবাই স্বাভাবিক যে PSPACE P-এর চেয়ে অনেক বড়। PSPACE-এ এমন এমন সব প্রবলেম্ আছে যেগুলোর polynomial সময়ের কোনও algorithm আজ অবধি কেউ বের করতে পারেনি। কিন্তু কেউ কোনোদিন পারবে না এটাই বা বলা যায় কীকরে? হয়তো খুব বুদ্ধিমান কোনও গবেষক কোনোদিন এরকম একটা algorithm বের করলেন। আসলে কিছু জিনিস কোনোদিন কেউ করতে পারবে না – এই ব্যাপারটা গাণিতিকভাবে প্রমাণ করা খুব শক্ত। তাই এরম কিছু প্রমাণ করার কোনও উপায় বের হলে খুব সুবিধে হবে – কমপ্লেক্সিটি ক্লাসগুলো কোনটা কার চেয়ে বড় সেটা শেষমেশ বোঝা যাবে। আর P বনাম NP সমস্যাটা তো আছেই – ওটা একদম কোহিনুর। তবে ওটার সমাধান করার ধারেকাছেও আমরা নেই। তবে এগুলোর কোনও একটা নিয়ে কিছুটা এগোনো গেলেও আমি বেশ খুশি হবো।
রাজীবুলঃ এই P বনাম NP প্রবলেম্টায় কি এটা জিজ্ঞাস্য যে P আর NP সমান কিনা [৪]?
জনঃ ঠিক তাই। প্রায় কেউই বিশ্বাস করে না P আর NP সমান, কিন্তু কিকরে সেটা দেখানো যাবে কেউ জানে না। যখন ইন্টারভিউয়ের শুরুতে আমি বলেছিলাম যে কিছু সমস্যা সমাধান করতে কম্পিউটার-এর অনেক বেশি সময় লাগে, সেটা বলেছিলাম বর্তমানে যা যা algorithm জানা গেছে, সেইগুলোর কথা মাথায় রেখে। এমন হতেই পারে যে দারুণ কোনও algorithm এইসব প্রবলেম্ খুব তাড়াতাড়ি সমাধান করে দিতে পারবে – সেটা শুধু আবিষ্কারের অপেক্ষায়। উৎপাদকে বিশ্লেষণ নিয়েও একই কথা প্রযোজ্য। আমরা সবাই মনে করি উৎপাদকে বিশ্লেষণ খুব কঠিন কাজ – এটাই cryptography-এর RSA cryptosystem-এর মূলে [৫]। কিন্তু এর কোনও গাণিতিক প্রমাণ নেই। কালকেই কেউ উৎপাদকে বিশ্লেষণ করার একটা algorithm বের করে RSA ভেঙ্গে দিতে পারে।
রাজীবুলঃ মানে একটা ক্লাসিক্যাল কম্পিউটারেও হতে পারে সেটা?
জনঃ একটা শক্তিশালী কোয়ান্টাম কম্পিউটার তো উৎপাদকে বিশ্লেষণ খুব তাড়াতাড়ি করতে পারেই, যদিও সেরম শক্তিশালী কোয়ান্টাম কম্পিউটার এখনো তৈরি হয়নি [৬]। কিন্তু ক্লাসিক্যাল কম্পিউটারেও হয়তো এমন কোনও algorithm আছে যা দিয়ে কোনও যৌগিক সংখ্যাকে সমান তাড়াতাড়ি উৎপাদকে ভাঙ্গা যায় [৭]। আমরা মনে করি সেটা করা শক্ত কারণ আমরা এখনো এটা করে উঠতে পারিনি – আর বিশেষ কোনো কারণ নেই।
রাজীবুলঃ তাই নাকি? খুব আশ্চর্যের তো!
জনঃ মানে, অনেক গুণী মানুষ অনেকদিন এটা চেষ্টা করে গেছেন, তাঁরা কেউ পারেননি – তাই কিছুটা আশ্বস্ত হওয়া যায় যে উৎপাদকে বিশ্লেষণের কোনও polynomial সময়ের algorithm নেই – প্রবলেম্টা সত্যি শক্ত। কিন্তু অন্য অনেকে মনে করেন এইরম ভাবার কোনও বৈজ্ঞানিক কারণ নেই। আমাকে যদি জিজ্ঞেস করেন, আমি খুব একটা জানি না কারা ঠিক আর কারা ভুল। শুধু এটাই বলতে পারি এরম কোনও polynomial সময়ের algorithm আমি বের করতে পারি নি – পারলে তো লিখেই ফেলতাম!
(এরপর আলোচনা অন্যদিকে ঘুরলো। এই অব্দি পড়ে যদি মনে প্রশ্ন জাগে, এই ধরণের গবেষণা করতে গেলে কীভাবে শুরু করা উচিত, কী বিষয় নিয়ে পড়া উচিত, তাহলে তার উত্তরটাই পাওয়া যাবে পরের অংশে।) (নিচে জন-এর গবেষণা-সংক্রান্ত বাকি আলোচনাটা দেওয়া হলো। বৈজ্ঞানিক জীবনে কোয়ান্টাম ইনফরমেশন তত্ত্বের আর জটিলতার তত্ত্বের মেলবন্ধনে থাকা বিভিন্ন বিষয় নিয়ে কাজ করেছেন জন। সেরকম কয়েকটা বিষয় নিয়েই একটু গভীরে গেলেন এখানে। বিষয়গুলো যেহেতু অত্যন্ত জটিল, উৎসাহী পাঠকদের জন্য জনের কথার সাথে সাথে থাকলো বেশ কিছু লিঙ্ক আর ফুটনোট।)

সৌমিকঃ আপনি এমন কিছু কমপ্লেক্সিটি ক্লাস নিয়ে কাজ করেছেন যেগুলিকে বিভিন্ন বস্তুর মধ্যে সহযোগিতামূলক (cooperating) বা প্রতিযোগিতামূলক (competing) ক্রিয়াপ্রতিক্রিয়ার দ্বারা ব্যাখ্যা করা যায়। সেগুলোর পেছনে ঠিক কী ভাবনা ছিল? এই ক্লাসগুলো ও আপনার গবেষণার ফলাফলগুলো নিয়ে যদি একটু বলেন।
জনঃ এই যে একাধিক কম্পিউটার-এর মধ্যে বিভিন্ন ক্রিয়া ও প্রতিক্রিয়া, যেখানে কম্পিউটারগুলোর লক্ষ্য আলাদা হতে পারে, এটা শুধু কমপ্লেক্সিটি থিওরি নয়, থিওরেটিক্যাল cryptography-তেও খুব গুরুত্বপূর্ণ। কমপ্লেক্সিটি থিওরিতে একটা ধারণা আছে – interactive proof system; এখানে এক বা একাধিক কম্পিউটার অন্য একটা কম্পিউটারের কাছে কিছু একটা গাণিতিক assertion প্রমাণ করতে চাইছে। এই interactive proof system কমপ্লেক্সিটি থিওরির অনেকটা জুড়ে রয়েছে। অনেক রিসার্চ হয়েছে এটা নিয়ে; খুব গুরুত্বপূর্ণ কিছু ফলাফলও পাওয়া গেছে।
কোয়ান্টামের ক্ষেত্রেও interactive proof system সমানভাবে গুরুত্বপূর্ণ। এখানে কম্পিউটারগুলো শুধু ক্লাসিক্যাল কোনও message (বার্তা) নয়, entangled কোনও কোয়ান্টাম অবস্থাকেও (quantum state) নিজেদের মধ্যে পাঠাতে পারে। অঙ্কের দিক থেকে entanglement খুব মজার; entanglement এর গাণিতিক চিত্রটা পরিষ্কার হলে interactive proof system এর অনেক কিছুও পরিষ্কার হয়ে যায়। যেমন ধরুন ঠিক দুটো কম্পিউটার আছে, আর তারা পরস্পরকে pure state পাঠাচ্ছে [৮], যেটা entangled ও হতে পারে – এই ব্যাপারটা নিয়ে অনেক রিসার্চ হয়েছে [৯]।
রাজীবুলঃ কোয়ান্টাম ইনফরমেশন তত্ত্বের এমন একটা সমস্যার কথা বলুন যা দশ বছরের মধ্যে সমাধান হয়ে গেলে আপনার খুব ভালো লাগবে।
জনঃ তার নাম SIC-POVM প্রবলেম্ বা symmetric information-complete positive operator valued measurement প্রবলেম্ [১০]। আমি নিজেও খুব চেষ্টা করেছি এটা। মাঝে মাঝে মনে হয়েছে সমাধানের প্রায় কাছাকাছি চলে এসেছি – কিন্তু শেষমেশ কিছুই হয়নি। কীভাবে হবে সেটাও এখনো জানিনা। এই সমস্যাটা কেউ সমাধান করতে পারলে খুব ভালো লাগবে।
প্রচ্ছদের ছবি: বিভিন্ন complexity class বা জটিলতার শ্রেণী। কোন শ্রেণী যে কোন শ্রেণীর অন্তর্ভুক্ত, সেসব এখনো গবেষণার বিষয়। (ছবির সূত্র)
কৃতজ্ঞতা স্বীকার: ইন্টারভিউটা ট্রান্সক্রাইব করেছে “বিজ্ঞান” টিমের সৌমিক ঘোষ। ইংরেজি থেকে বাংলায় অনুবাদ করেছে “বিজ্ঞান” টিমের শৌর্য সেনগুপ্ত। অনুবাদে সাহায্য করেছে “বিজ্ঞান” টিমের অনির্বাণ গঙ্গোপাধ্যায় ও সৌমিক ঘোষ।
উৎসাহী পাঠকদের জন্য
[১] কমপ্লেক্সিটি ক্লাস নিয়ে আরেকটু বিশদে জানতে “বিজ্ঞান”-এর এই লেখাটা পড়ে দেখতে পারোঃ কমপ্লেক্সিটি থিওরির মজার জগৎ – বিজ্ঞান।
[২] স্পেস মানে মেমরি। সময়ের সাথেসাথে কতটা মেমরি ব্যাবহার করছি সেটাও মাঝেমাঝে দেখা হয়। মানে, এই ধরো ল্যাপটপ ধরলে কতটা RAM বা hard drive-এর স্পেস খরচ হল।
[৩] P একটা সেট, যেখানে সেইসব গণনামূলক কাজ আছে যা একটা ক্লাসিক্যাল কম্পিউটার তাড়াতাড়ি করে ফেলতে পারবে। কতটা তাড়াতাড়ি? সময়টা হবে কম্পিউটারটার ইনপুটের সাইজের সাথে বহুপদী (বা polynomially related)। PSPACE-ও একটা সেট, যেখানে সেইসব গণনামূলক কাজ আছে যা একটা বিশেষ ধরণের ক্লাসিক্যাল কম্পিউটার করতে পারবেঃ এমন একটা কম্পিউটার যার মেমরির সাইজটা তার ইনপুটের সাইজের সাথে polynomially related। PSPACE-এ কিন্তু কতটা সময় লাগছে সে বিষয়ে কিছুই বলছি না – সময়টা ইনপুটের সাইজের সাথে polynomially related হতে পারে, কিংবা তার বেশিও সময় লাগতে পারে; আমাদের তাতে যায় আসে না, আমাদের কারবার মেমরির সাইজ নিয়ে। একটু ভাবলেই দেখবে, যদি এক একক সময়ে এক একক মেমরি ব্যাবহার করি, তাহলে ‘polynomial’ সময়ে ‘polynomial’-এর চেয়ে বেশি মেমরি ব্যাবহার করা সম্ভব নয়। তাই, যা কিছু গণনামূলক কাজ P সেটটায় আছে, সব PSPACE সেটটাতেও আছে।
[৪] এই প্রশ্নটা নিয়ে আরেকটু জানতে এই লেখাটা পড়তে পারো। প্রশ্নটাকে সর্বকালের অন্যতম সেরা অমীমাংসিত প্রশ্ন বলা হয়।
[৫] RSA অর্থাৎ Rivest, Shamir ও Adleman: এই তিন মানিকজোড় একটা cryptographic system বানিয়েছিলেন। এটা বহু ক্ষেত্রে ব্যাবহার হয়। ফ্লিপকার্ট থেকে যখন কেনাকাটা করছ, তোমার ক্রেডিট কার্ড নম্বর কোনও হ্যাকার জানতে পারছে না কেন? তার মূলে RSA। কোনও কোম্পানির মধ্যে কেউ একই কোম্পানির অন্য কারোকে একটা ফাইল পাঠাচ্ছে ই-মেলে, ফাইলটা অন্য কোম্পানির কেউ চুরি করতে পারছে না কেন? তার মূলেও RSA। RSA-কে খুব সহজ করে বোঝানো যায়। ধরো তুমি আর তোমার বন্ধু একটা ফাইল পাঠাতে চাও। তোমার কাছে একটা মৌলিক সংখ্যা আছে, তোমার বন্ধুর কাছে আরেকটা মৌলিক সংখ্যা আছে – দুটো সংখ্যাই ঐ একজন ছাড়া আর কেউ জানে না। আর আছে একটা কম্পিউটার নেটওয়ার্ক – যাতে করে ফাইলটা পাঠাবে। নেটওয়ার্কটা তোমাদের দুজনের থেকে দুটো মৌলিক সংখ্যা নেবে; তোমার মৌলিক সংখ্যাটা দিয়ে ফাইলটাকে encrypt (বা পরিবর্তন) করবে; দুটো গুন করে একটা যৌগিক সংখ্যা করবে; আর তোমার বন্ধুকে পাঠাবে encrypted ফাইলটা এবং ঐ যৌগিক সংখ্যাটা। Encryption-টা এমনভাবে হবে যে কেবলমাত্র তোমার মৌলিক সংখ্যাটা পেলেই ফাইলটাকে আবার আগের অবস্থায় ফেরানো যাবে (বা decrypt করা যাবে)। মানে তোমার মৌলিক সংখ্যাটা অনেকটা সিন্দুকের চাবির মত। কিন্তু যেহেতু তোমার বন্ধু যৌগিক সংখ্যাটার একটা উৎপাদক জানে, অন্যটা – মানে তোমার সংখ্যাটা – ভাগ করেই পেয়ে যাবে। তোমার সংখ্যাটা পেয়ে গেলে সে ফাইলটাও decrypt করতে পারবে। এবার ধরো কোনও হ্যাকার নেটওয়ার্কটা হ্যাক করে যৌগিক সংখ্যাটা আর ফাইলটা পেয়েছে। কিন্তু তাতে তার লাভ নেই কিছু, তার যে চাই তোমার মৌলিক সংখ্যাটা! যেহেতু বড় সংখ্যাটার উৎপাদকে বিশ্লেষণ করা খুব শক্ত কাজ, ঐ যৌগিক সংখ্যাটা যদি খুব বড় হয়, সেটাকে উৎপাদকে বিশ্লেষণ করে তোমার মৌলিক সংখ্যাটা পেতে পেতে এত সময় লাগবে যে হয়তো তারমধ্যে পৃথিবীই ধ্বংস হয়ে যাবে।
[৬] P-এর মতই আছে BQP: এটা এমন একটা সেট যেখানে সেইসব গণনামূলক কাজ আছে যা একটা কোয়ান্টাম কম্পিউটার তাড়াতাড়ি করে ফেলতে পারবে। তাড়াতাড়ি মানে আবার ঐ polynomial সময়ে। উৎপাদকে বিশ্লেষণ BQP সেটটায় আছে। Peter Shor সেটাই দেখিয়েছিলেন।
[৭] ‘সমান তাড়াতাড়ি’ বলতে polynomial সময়ে। অর্থাৎ, এমন হতেই পারে যে ‘উৎপাদকে বিশ্লেষণ’ সমস্যাটা P সেটটায় আছে।
[৮] Pure state নিয়ে পড়তে হলে এই লিঙ্কটা দেখতে পারো। কোয়ান্টাম entanglement নিয়ে পড়তে হলে এইটা। দ্বিতীয় লিঙ্কটা পড়লেই বুঝতে পারবে pure state-ও ‘entangled’ হতে পারে। কম্পিউটার সায়েন্সের আর ফিজিক্সের বহু ক্ষেত্রে কোয়ান্টাম entanglement দেখা যায়। কয়েকটা উদাহরণ দ্বিতীয় লিঙ্কটায় আছে।
[৯] ধরো তোমার প্রিয় বান্ধবীর ক্রিকেটে বিশেষ জ্ঞান নেই। একদিন তোমাকে সে জিজ্ঞেস করে বসেছে, দাদা না ধোনি – কে বড় ক্রিকেটার আর কেন। তুমি তো দাদার ভক্ত – প্রমাণ করেই ছাড়বে বাইশ গজে দাদা ধোনির থেকে অনেক বড়। তবে বান্ধবীটি সহজে গলবার নয়; যতবারই কিছু প্রমাণ দিচ্ছ, সে পাল্টা প্রশ্ন করে তোমাকে ভালোই যাচাই করে নিচ্ছে। এইভাবেই বিভিন্ন রাউন্ডে তোমাদের কথোপকথন চলছে। কিংবা ধরো এই ছবিটাই, কিন্তু তোমার সঙ্গে আছে সারাদিন তোমার পেছনে লাগা ক্লাসের সেই ফাজিল ছোকরা। তুমি যাই বল, বান্ধবীর সামনে তোমার প্রেস্টিজ পাংচার করতে সেই ছোকরা বলে ঠিক তার উলটো কথা। তুমি যদি দাদার সাপোর্টে ২০০২ ন্যাটওয়েস্ট ট্রফির কথা বল, সে বলছে ধোনির সাপোর্টে ২০১১ বিশ্বকাপ। এবার ধরো এইসব ক্ষেত্রে মানুষের জায়গায় কম্পিউটার আছে, আর গরমাগরম আলোচনার টপিকটা এনকোড করা আছে কাঠখোট্টা গাণিতিক ভাষায়। জন এই ধরণের interaction নিয়ে প্রচুর গবেষণা করেছেন। যদি শুধু তুমি আর তোমার বান্ধবী থাকো, তোমাদের কথোপকথনের সঙ্গে কমপ্লেক্সিটি থিওরির যে ক্লাসের সাদৃশ্য সে হল QIP (quantum interactive proofs)। আর তুমি, ফাজিল, ও তোমার বান্ধবী থাকলে তাকে বলে QRG (quantum refereed games)। নামগুলো হিব্রু শোনাচ্ছে? এই লিঙ্কগুলো পড়লে কিছুটা সম্যক ধারণা করতে পারবে।
- QIP: https://en.wikipedia.org/wiki/QIP_(complexity)
- QRG: https://en.wikipedia.org/wiki/Quantum_refereed_game
[১০] খুব সহজভাবে বললে প্রবলেম্টা জিজ্ঞেস করছে, একটা খুব বিশেষ ধরণের কোয়ান্টাম measurement সব dimension-এ বিদ্যমান কিনা। কোয়ান্টাম measurement নিয়ে জানতে হলে এই লিঙ্কটা পড়ে দেখতে পারো। SIC-POVM নিয়ে জানতে হলে এইটা।