লেখাটির প্রথম পর্বে আমরা দেখেছিলাম মানুষের জন্য আপাত সহজ কিছু কাজ করতে একটা যন্ত্রকে কতটা কাঠখড় পোড়াতে হয়। একটা ছবি চেনা কিংবা লিখিত শব্দের মর্মোদ্ধার করা, যেগুলো মানুষ অবলীলায় করতে পারে, সেগুলোই একটা যন্ত্রকে ধরে ধরে শেখানো প্রায় অসম্ভবের পর্যায়ে পরে। এই পর্বে আমরা এই সমস্যার একটি সমাধান দেখবো।
সনাতন এ আই–এর সীমাবদ্ধতা
সনাতন এ আই-এর ভিত্তি ছিল যুক্তিবাদ, অর্থাৎ প্রতিটি বুদ্ধির কাজকে বিশ্লেষণ করে বোঝার চেষ্টা করা হয়েছে কিভাবে কম্পিউটারকে এই ক্ষমতা দেওয়া যেতে পারে। তাতে সব ক্ষেত্রেই কিছু সরল সমস্যার সমাধান হলেও, বাস্তবের অনেক সমস্যাই ধরাছোঁয়ার বাইরে থেকে গেছে। অথচ একটু খেয়াল করলেই বোঝা যায়, আমাদের ক্রিয়াকলাপ প্রায়ই আমাদের অজান্তে অবচেতন থেকে নিয়ন্ত্রিত হয়। আশপাশটা দেখে বুঝে বা চিনে নেওয়া, কথা বলা এবং শোনা, এসবের জন্য আমরা কখনও ভাবতে বসিনা। সনাতন এ আই-তে ধরা হোতো যন্ত্রের কার্যকলাপে বুদ্ধির প্রকাশের জন্য প্রয়োজন অনুভব – বোধ – কর্ম এমন একটি চক্রাকার নিয়ন্ত্রণ ব্যাবস্থা। অনুভব হলো কাজের উপযোগী একাধিক সেন্সর থেকে যে তথ্যের ধারা আসতে থাকে, তাদের সঞ্চয় করা। বোধ হোলো এই তথ্যের বিশ্লেষণ করে পরিবেশের সম্বন্ধে একটি ধারণা করা, বা পরিবেশের একটি মডেল তৈরি করা। এই মডেলের ভিত্তিতে, লক্ষ্য অনুযায়ী, যুক্তি, তর্ক ও অন্বেষণের মাধ্যমে স্থির করা হয় যন্ত্রের কি করা উচিত।
অবিরাম কম্পিউটার এই নিয়ন্ত্রণ চক্র মেনে চলতে থাকে, যাতে পরিবেশে হঠাৎ কোনও পরিবর্তন হলেও যন্ত্র তা মানিয়ে নিতে পারে। এই নিয়ন্ত্রণ চক্রটি আমাদের সাধারণ বুদ্ধিতে বেশ যুক্তিগ্রাহী মনে হলেও, এতে প্রছন্ন আছে ‘বুদ্ধির ভিত্তি যুক্তি’ এমন একটি ধারণা। এর বিকল্প যে বুদ্ধির গঠন হতে পারে তা হোলো সরাসরি অনুভব থেকে কর্ম এমন একটি নিয়ন্ত্রণ চক্র। এতে যুক্তি তর্কের কোনও বালাই নেই। অনেকটা অবচেতন থেকে শুধু অনুভবের ভিত্তিতে কাজ স্থির করা। এই উদ্দেশ্যে প্রস্তাবিত হোলো মস্তিষ্কের স্নায়বিক জালের অনুকরণে আর্টিফিশিয়াল নিউরাল নেটওয়ার্ক (artificial neural network), অর্থাৎ কৃত্রিম স্নায়বিক জাল, সংক্ষেপে এ এন এন।
সনাতন এ আই-তে ধরা হোতো যন্ত্রে বুদ্ধির প্রকাশের জন্য প্রয়োজন অনুভব – বোধ – কর্ম, এমন এক চক্রাকার নিয়ন্ত্রণ ব্যাবস্থা।
নিউরাল নেটওয়ার্ক–এর জন্ম
এর ভাবনা চিন্তা শুরু হয়েছিল চল্লিশের দশক থেকেই, যখন কম্পিউটারের গঠন কেমন হবে সে বিষয়ে স্পষ্ট ধারণা ছিল না। এর প্রধান অঙ্গ ছিল উদাহরণ থেকে কাজ শেখার ক্ষমতা। এই সময় যে ধরনের নিউরনের কথা ভাবা হয়েছিল, তার ইনপুট আর আউটপুটের মধ্যে সম্পর্কটা ছিল সরলরৈখিক, তাই এর ক্ষমতা ছিল সীমিত। সত্তরের দশকে মারভিন মিন্সকি ‘পারসেপ্ট্রন’ নামে একটি বইয়ে [১] এর বিস্তারিত বিশ্লেষণ করে এই সিদ্ধান্তে আসেন যে নিউরাল নেটওয়ার্ক কখনওই কোনো কঠিন কাজ শিখতে পারবে না। এর ফলস্বরূপ বেশ কিছু বছর এই বিষয়ে গবেষণা প্রায় বন্ধ থাকে। এরপর আশির দশকের শেষার্ধে রুমেলহার্ট ও আরও অনেকে অরৈখিক (নন লিনিয়ার) নিউরনের নেটওয়ার্ক বানিয়ে তাকে কিভাবে কাজ শেখানো যায় তা দেখালেন [২]। তার সফল প্রয়োগ হলো অনেক ক্ষেত্রে। এরপর আবার এ এন এন নিয়ে নতুন করে আগ্রহ জন্মালো সবার মনে। কৃত্রিম নিউরন একটি অতি সরল গণকযন্ত্র যে তার ইনপুট থেকে কেবল একটি নির্দিষ্ট সূত্র অনুযায়ী আউটপুট গণনা করে। নিচের ছবিতে এই ধরণের নিউরন দিয়ে গঠিত একটা স্নায়ুতন্ত্রের ছবি দেওয়া হলো।
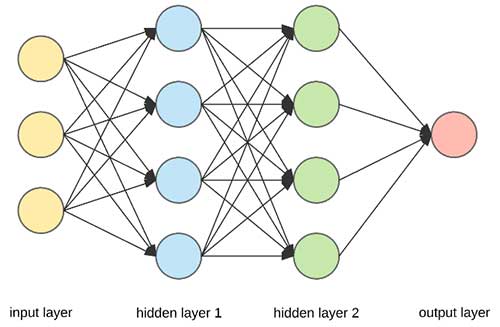
স্তরপূর্ণ নিউরাল নেট – বাঁয়ে ইনপুট স্তর, মাঝে দুটি গুপ্ত স্তর, ডাইনে আউটপুট স্তর। প্রতিটি স্তর তার পরের স্তরের সাথে সম্পূর্ণ ভাবে সংযুক্ত (ছবির সূত্র)
যে সূত্রের মাধ্যমে আউটপুট গণনা হয়, সেটা নানারকম হতে পারে। কিন্তু তা অবশ্যই সরলরৈখিক নয়, অর্থাৎ ইনপুট কিছুটা পরিবর্তন হলে আউটপুট সেই অনুপাতেই পরিবর্তিত হবে এমন নয়। উপরের ছবিটির মতো একটি নিউরন অন্য অনেক নিউরনের থেকে একত্রে ইনপুট নিতে পারে, আবার তার আউটপুট অন্য অনেক নিউরনের ইনপুটে পৌঁছে দিতে পারে। একটি নিউরনের আউটপুট থেকে আরেকটি নিউরনের ইনপুটে বার্তা যাওয়ার পথে আছে নিয়ন্ত্রণকারী একটি ভার (ওয়েট) যেটি ঠিক করে দেয় দ্বিতীয় নিউরনের সক্রিয়তায় প্রথম নিউরনের অবদান কতটা থাকবে। নিউরনগুলি নিজেদের মধ্যে নানারকমভাবে সংযুক্ত থাকতে পারে। একটি সংযোগের ভার ঠিক করে দেয় তার সক্রিয়তা কেমন হবে। একটি নিউরাল নেটকে শেখানো মানে হচ্ছে তাদের সংযোগের ভারগুলির মান ঠিক করে দেওয়া, যাতে তারা শেখানো আচরণটি অনুসরণ করতে পারে।
ইনপুট, আউটপুট ও গুপ্ত স্তর
পারস্পরিক সংযোগের ধরণের উপর নির্ভর করে নানারকম নিউরাল নেট বানানো যায়। এখানে বিশেষ ভাবে যে নিউরাল নেটের কথা আলোচিত হবে তার নিউরনগুলি ইনপুট থেকে আউটপুট অবধি স্তরে স্তরে সাজানো। ইনপুট স্তরের নিউরনগুলি সমস্যার বিবরণ গ্রহণ করে। আউটপুট স্তরের নিউরনগুলির মাধ্যমে সমস্যার সমাধান পাওয়া যায়। যেমন, হাতে লেখা সংখ্যা চেনা যদি এর উদ্দেশ্য হয়, তাহলে ইনপুট স্তরের নিউরনগুলিতে ইনপুট হবে একটি হাতে লেখা সংখ্যার চিত্রের প্রতিটি বিন্দুর ঔজ্জ্বল্য। তেমনি আউটপুট স্তরের এক একটি নিউরন এক একটি সংখ্যার প্রতিনিধি হিসাবে গণ্য হতে পারে। অর্থাৎ, যে আউটপুট নিউরনের সক্রিয়তা সবচেয়ে বেশি, সে সংখ্যার চিত্রই ইনপুট করা হয়েছে বলে মানা হবে। ইনপুট এবং আউটপুট স্তরে কতগুলি করে নিউরন থাকা উচিত, তা নির্ভর করে সমস্যার প্রকৃতির উপর। সংখ্যার চিত্র যদি বর্গাকার ১০ x ১০ বিন্দুতে ঔজ্জ্বল্য দিয়ে বর্ণিত হয়, তাহলে ইনপুট স্তরে ১০০ টি নিউরনের প্রয়োজন। আউটপুট যেহেতু ০ থেকে ৯ এই দশটি সংখ্যাই শুধু হতে পারে, আউটপুট স্তরে প্রয়োজন মাত্র ১০ টি নিউরনের।
এতো হলো ইনপুট এবং আউটপুট স্তরের কাহিনী। এদের মাঝে থাকে এক বা একাধিক গুপ্ত নিউরনের স্তর বা হিডেন লেয়ার (hidden layer)। প্রথম গুপ্ত স্তরের প্রতিটি নিউরনের ইনপুট আসে ইনপুট স্তরের প্রতিটি নিউরনের আউটপুট থেকে, তাদের সংযোগের ভার অনুযায়ী। তেমনি গুপ্ত স্তরের প্রতিটি নিউরনের আউটপুট প্রেরিত হয় তার পরের গুপ্ত স্তরের প্রতিটি নিউরনের ইনপুটে (কিংবা যদি একটিই গুপ্ত স্তর থাকে, তাহলে তার আউটপুট প্রেরিত হয় আউটপুট স্তরের প্রতিটি নিউরনের ইনপুটে)। প্রত্যেকটি স্তরের প্রতিটি নিউরন তার ইনপুটে প্রাপ্ত সমস্ত বার্তাকে মিলিয়ে তার উপর গণনা করে আউটপুট বার্তা তৈরি করে [২]। এইভাবে অবশেষে আউটপুট স্তরে প্রকাশিত হয় সমাধান।
খুব স্বাভাবিক ভাবেই এই সমাধান নির্ভর করে নিউরনগুলির পারস্পরিক সংযোগের ভারের বর্তমান মানের উপর। সমাধানকে কার্যকরী করার জন্য সমস্ত ভারের উপযুক্ত মান হওয়া দরকার। রুমেলহার্ট ও তার সহকর্মীরা ব্যাকপ্রপাগেশন আ্যলগরিদম (backpropagation algorithm) তৈরি করলেন অনেক উদাহরণ থেকে এই ভারগুলির মান স্থির করার জন্য। এটি অবশ্য এক দফায় হয় না। অনেক উদাহরণকে বারবার দেখিয়ে ধীরে ধীরে নেটওয়ার্ক তার সমস্ত সংযোগের ভারের মান বেঁধে নেয়। প্রতিটি উদাহরণে সমাধানে যে পরিমাণ ভুল হোলো, তার উপর ভিত্তি করে পেছনের প্রতিটি স্তরের সংযোগের ভার উপর নিচ করে ভুল কমানোই এই আ্যলগরিদমের উদ্দেশ্য। সহজ সরল হলেও এই আ্যলগরিদম খুবই কার্যকরী প্রতিপন্ন হয়েছে। এর ব্যবহার এখনও অব্যাহত, যদিও ক্ষেত্র অনেক বদলে গেছে।
নিউরাল নেটওয়ার্ক কদ্দুর যেতে পারে
নব্বইয়ের দশকে এ এন এন-এর অনেক প্রয়োগ হয়েছিল তথ্যের শ্রেনীবিভাগ বা তার মধ্যে কোনও বিশেষ জিনিস বা প্যাটার্নকে চেনার জন্য। এগুলি অন্য অনেক পদ্ধতিতেও করা সম্ভব ছিল, কিন্তু এ এন এন-এর এই প্রাথমিক পরীক্ষায় পাশ করাটা জরুরি ছিল। এ এন এন এর ক্ষেত্রে নতুন ছিল ইনপুট এবং আউটপুট কিরকম হবে, কোন স্তরে কটি নিউরন হলে ঠিক হয়, এই সবের বিচার। তাছাড়া প্রয়োজন ছিল অনেক উদাহরণের, যার থেকে এর সম্যক শিক্ষা সম্ভব হতে পারে। এ এন এন ঠিক কিভাবে কাজ করে তা নিয়ে অনেক ভাবনা চিন্তা হয়েছে এই সময়। বোঝা গেলো এর প্রতিটি স্তর তার নিচের স্তরের তথ্যের মধ্যে যে বৈশিষ্ট্য আছে তাকে প্রকাশ করার চেষ্টা করে। এইভাবে অনেক স্তরের মধ্যে দিয়ে প্রায় যে কোনো সমস্যার সমাধান শিখে নেওয়া যেতে পারে।
কিন্তু দেখা গেলো স্তরের সংখ্যা বাড়ালে শিক্ষার সময় নিচের স্তরের সংযোগের ভারে প্রায় কোনো পরিবর্তনের ঢেউ এসে পৌঁছচ্ছে না। তাই বিশেষ কঠিন সমস্যার সমাধান এ এন এন এর এক্তিয়ারের বাইরেই রয়ে গেলো। এছাড়া অন্য সমস্যাও ছিল। অনেক সমস্যা সমাধানেই, যেমন ক্যামেরার ছবির বিশ্লেষণে, ইনপুট স্তরে বহুসংখ্যক নিউরনের প্রয়োজন হয়। এতে অনেক বেশি সংযোগ ভারের আমদানি হয়, আর তাদের শিক্ষার জন্য প্রয়োজন হয় অসংখ্য উদাহরণ, যা সংগ্রহ করে ভার শিক্ষায় ব্যবহার করাটা প্রায় অসম্ভব হয়ে ওঠে। এর ফলে ধীরে ধীরে এ এন এন এর প্রতি গবেষকদের আগ্রহ কমে যাচ্ছিল। এর পর ২০০৬ এ বহুস্তরীয় এ এন এন এর শিক্ষার বিষয়ে একটি নতুন ধারণা এলো ক্যানাডার কয়েকজন বৈজ্ঞানিকের কাছ থেকে। শুরু হোলো ডীপ লার্নিং (deep learning) বা গভীর শিক্ষার অভিযান।
আরো একবার সম্ভাব্য ব্যর্থতার মুখে দাঁড়িয়ে কৃত্রিম বুদ্ধিমত্তার সম্ভাবনা মাথা চাড়া দিয়ে উঠলো। কথা বলে নিজের বক্তব্য পেশ করা, অন্যের কথা শুনে বোঝা, আশপাশের অজস্র জিনিসকে চিনে নেওয়া, এগুলো আমরা ঠিক কিভাবে করি তা কয়েকটি স্পষ্ট নিয়ম দিয়ে বাঁধা প্রায় অসম্ভব বলে মনে হচ্ছিল সনাতন যুক্তিভিত্তিক এ আই তে। আশা ছিল এ এন এন এই জটিল সমস্যার সমাধান শিখে নেবে প্রচুর উদাহরণ থেকে। তার জন্য প্রয়োজন বহুস্তরীয় এ এন এন। কিন্তু শুধু ব্যাক প্রপাগেশন অ্যালগরিদম দিয়ে এমন বহুস্তরীয় নেটের সন্তোষজনক শিক্ষা হচ্ছিল না।
কিছু রেফারেন্স:
[১] Perceptrons: an introduction to computational geometry, by Marvin Minsky and Seymour Papert
[২] নিউরাল নেটওয়ার্ক-এ কিভাবে ননলিনিয়ার গণিত ব্যবহৃত হয়, তার কয়েকটি সহজ উদাহরণ এখানে দেখুন।
[৩] Krizhevsky, Alex & Sutskever, Ilya & Hinton, Geoffrey. (2012). ImageNet Classification with Deep Convolutional Neural Networks. Neural Information Processing Systems. 25. 10.1145/3065386.[৪] Geoffrey E. Hinton, Simon Osindero, and Yee-Whye Teh. 2006. A fast learning algorithm for deep belief nets. Neural Comput. 18, 7 (July 2006), 1527–1554. DOI:https://doi.org/10.1162/neco.2006.18.7.1527

nice