এই ধারাবাহিকের আগের পর্বে আমরা দেখেছিলাম যে রামধনু তৈরি করতে শুধুমাত্র একটি জলকণাই যথেষ্ট। প্রতিসরণ ও প্রতিফলনের সূত্র মেনে রামধনু তৈরি হয় এবং তারা একাধিক প্রকারের হয়। কিন্তু সাথেসাথে যে অতিরিক্ত ধনুর আবির্ভাব হয়, তার ব্যাখা এভাবে পাওয়া যায় না। প্রাথমিক ও মাধ্যমিক রামধনুর মাঝের আকাশই বা সবসময় বেশি গাঢ় দেখায় কেন? এর ব্যাখা কি আলোর প্রতিফলন ও প্রতিসরণের মাধ্যমে সম্ভব?

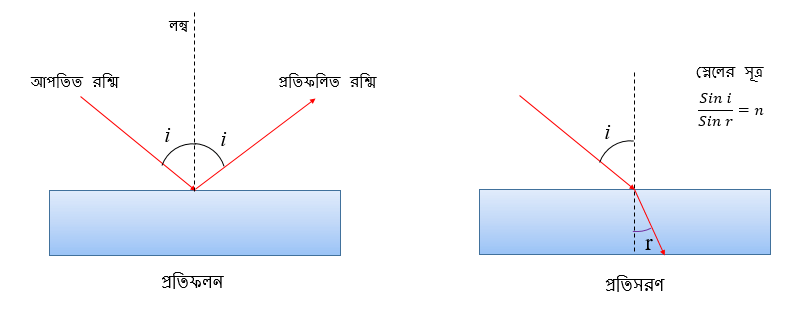
প্রতিফলন ও প্রতিসরণের সূত্রের সাথে তো তোমরা সকলেই কমবেশী পরিচিত, তাও একবার নিচের ছবিগুলির মাধ্যমে তোমাদের একটু মনে করিয়ে দিই।

প্রতিফলনে আপতন আর প্রতিফলন কোণের মান সমান হয় (ছবিতে i)। অন্যদিকে প্রতিসরণে স্নেলের সূত্র খাটে। মাধ্যমের প্রতিসরাঙ্ক (ছবিতে n) জানলে প্রতিসরণ কোনের মান (ছবিতে r) খুব সহজেই বের করা যায় এই নিয়ম কাজে লাগিয়ে।

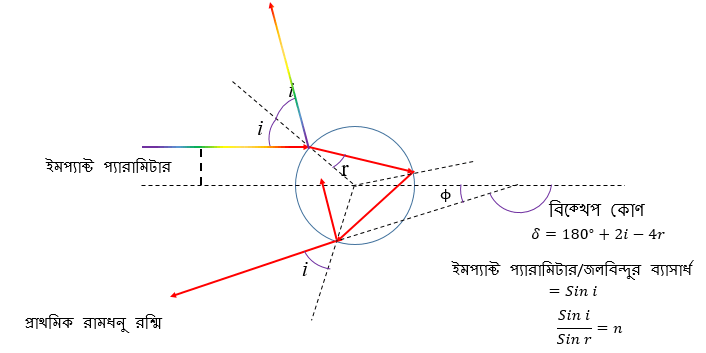
রামধনুর প্রাথমিক বিশ্লেষণ এই দুই নীতির উপর ভিত্তি করেই শুরু হয়েছিল। এখন বিশ্লেষণের সুবিধার জন্য ধরে নেওয়া যাক যে আকাশে ভাসমান জলবিন্দুরা গোলাকৃতি। কি সুবিধা তাতে? সুবিধা এই যে গোলকের প্রতিসাম্যর (symmetry) দরুন আপতিত আলোকরশ্মির দিশা নিয়ে আমাদের মাথা ঘামানোর কোন দরকার নেই। কারণ গোলকের কাছে সমস্ত দিকই সমান। শুধু যেটা বিবেচ্য সেটা হল গোলকের কেন্দ্রবিন্দু থেকে আলোকরশ্মির লম্ব দুরত্ব।

এই দুরত্বকে বিজ্ঞানের পরিভাষায় বলা হয় ইমপ্যাক্ট প্যারামিটার (impact parameter)। যদি আলোকরশ্মি সরাসরি গোলকের কেন্দ্রবিন্দু ভেদ করে, তাহলে তার ইমপ্যাক্ট প্যারামিটার শূন্য। আর যদি তা গোলকটিকে স্পর্শ করে বেরিয়ে যায় তাহলে তার ইমপ্যাক্ট প্যারামিটার-এর মান গোলকের ব্যাসার্ধের সমান (এটি ইমপ্যাক্ট প্যারামিটার-এর সর্বোচ্চ মানও বটে)। নিচের ছবিটি দেখ, ইমপ্যাক্ট প্যারামিটার-এর ধারণা আরো পরিষ্কার হবে।

ভেবে দেখলে, রামধনুর ব্যাপারটা অবাক করার মতই। যে সূর্যরশ্মি জলকণার উপর এসে পড়ছে, তাদের ইমপ্যাক্ট প্যারামিটার-এর মান শূন্য থেকে জলকণার ব্যাসার্ধের মাঝে যা খুশি হওয়া সম্ভব। আর তাহলে, বিক্ষিপ্ত রশ্মিদের বিক্ষেপ কোণও শূন্য ও ১৮০° র মাঝে যে কোন মান  নিতে পারে, তাই নয় কি? তাহলে আকাশের একটা বিশেষ কোণেই শুধু রামধনু দেখতে পাওয়া যাবে কেন? থিওডোরিক এটা ভেবে দেখেননি। এই প্রশ্নের উত্তর প্রথম মেলে ডেকার্টের কাছে।

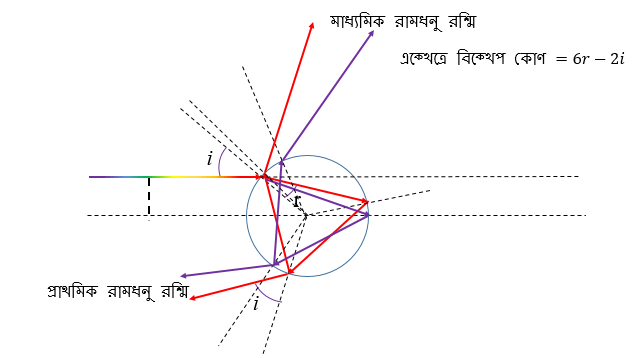
একটু ভাল করে এই প্রশ্নটা ভেবে দেখা যাক। উপরের ছবিটি দেখ – খুব সহজ জ্যামিতি লাগিয়ে আমরা বিক্ষেপ কোণ বা স্ক্যাটারিং অ্যাঙ্গেল (scattering angle), δ-র মান বের করার একটা সমীকরণ লিখেছি। এই সমীকরণ অনুযায়ী আপতন আর প্রতিসরণ কোণের মান জানলেই বিক্ষেপ কোণের মান জানা যাবে।

উপরের ছবি অনুযায়ী ইমপ্যাক্ট প্যারামিটারের মান পাল্টালে, অর্থাৎ আলোক রশ্মি জলকণার বিভিন্ন জায়গায় এসে ধাক্কা মারলে, আপতন কোণ বা i-এর মান বদলাব‍ে (সমীকরণ ছবিতে দেওয়া হয়েছে)। এবং পরিণামে প্রতিসরণ কোণ বা r-এর মানেরও পরিবর্তন হবে। অর্থাৎ ইমপ্যাক্ট প্যারামিটার বদলালে বিক্ষেপ কোণ বদলাবে, তাই না? যেমন, আপতিত আলোকরশ্মির ইমপ্যাক্ট প্যারামিটার শূন্য হলে বিক্ষেপ কোণের মান হবে ১৮০°, অর্থাৎ বিক্ষিপ্ত আলোকরশ্মি প্রতিফলিত হয়ে সোজা যেদিক থেকে এসেছিল সেদিকেই ফিরে যাবে।

এবার ধরো, ইমপ্যাক্ট প্যারামিটার-এর মান যদি ক্রমাগত বাড়ানো যায়, তাহলে বিক্ষেপ কোণের মানের পরিবর্তনটা ঠিক কিরকম হবে? ডেকার্ট এই প্রশ্নেরই উত্তর খুঁজছিলেন।

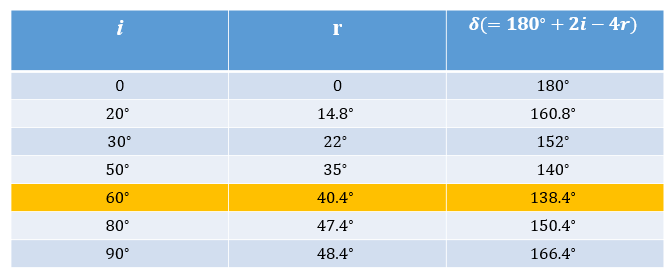
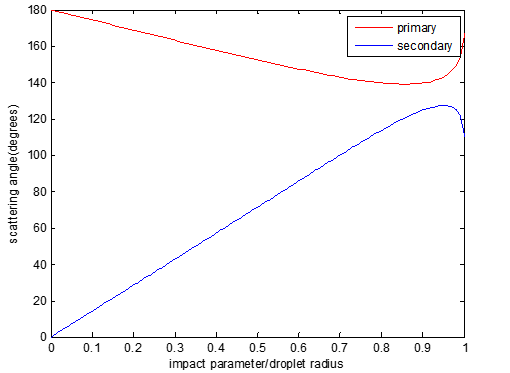
প্রাথমিক রামধনু রশ্মির ক্ষেত্রে দেখা গেল যে ইমপ্যাক্ট প্যারামিটার বাড়ানোর সাথে সাথে বিক্ষেপ কোণের মান প্রথমে কমতে থাকে, কিন্তু একটা সময় পর সেটা আবার বাড়তে শুরু করে! অর্থাৎ বিক্ষেপ কোণের একটি সর্বনিম্ন মান রয়েছে; হিসেব করে দেখা গেল যে এই সর্বনিম্ন মানটি হল ১৩৮°। ইমপ্যাক্ট প্যারামিটার জলবিন্দুর ব্যাসার্ধের ৭/৮ ভাগ হলে বিক্ষেপ কোণের মান এই দাঁড়ায়।

এখানে তোমরা হয়ত প্রতিবাদ করে বসবে! বলবে – “বিক্ষেপ কোণের মান হিসেব করতে আলোর প্রতিসরাঙ্কের মান জানতে হয়। আর এই যে সেদিন স্কুলে মাষ্টার মশাই দেখালেন, প্রিজমের মধ্যে দিয়ে সূর্যের আলো সাত রঙে ভেঙ্গে যায়। বিভিন্ন রঙের আলোর জন্য মাধ্যমের প্রতিসরাঙ্ক আলাদা – তাই না আলো সাত রঙে ভেঙ্গে গেল? তাহলে বিক্ষেপ কোণের মানও তো পালটাবে আলোর রঙ পাল্টালে?” সাবাশ তোপসে! ডিটেক্টিভের মত একদম ঠিক ধরেছ! এই বিক্ষেপ কোণের মান বিভিন্ন রঙের জন্য সত্যিই আলাদা। আর সেখানেই তো রামধনুর সৃষ্টি-রহস্য! বুঝতে যাতে আর একটু সুবিধা হয় তার জন্য নিচে একটি টেবিলে আপতন কোণ i-এর বিভিন্ন মানের জন্য বিক্ষেপ কোণের মান দেখিয়ে দেওয়া হল, শুধু বেগুনি রঙের আলোর জন্য। জলের জন্য বেগুনি রঙের প্রতিসরাঙ্ক 1.340।

ছবিটিতে দেখ, i = 60°-র জন্য δ-র মান সর্বনিম্ন। কোন ম্যাজিক নেই, শুধু যোগ-বিয়োগের খেলা! δ-র সমীকরণটি পাঠকদের মনে করিয়ে দেওয়ার জন্য আরেকবার লিখে দেওয়া হল।

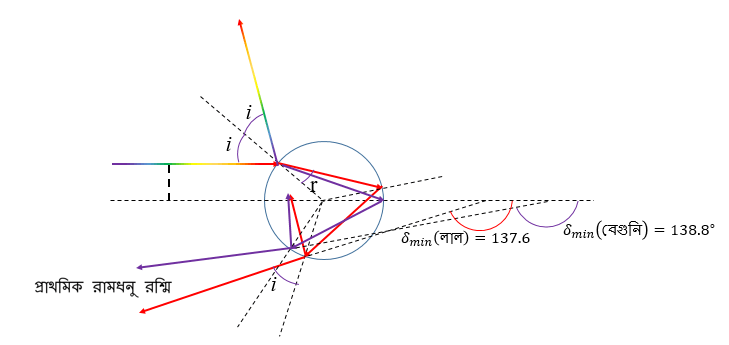
লাল রঙের জন্য বিক্ষেপ কোণ δ-র সর্বনিম্ন মান বেগুনির তুলনায় সামান্য কম, কারণ লাল রঙের জন্য জলের প্রতিসরাঙ্ক বেগুনির তুলনায় কম (1.331)। অর্থাৎ বেগুনির প্রতিসরণ লালের তুলনায় বেশি। নিচের ছবিটি দেখ; ব্যাপারটা আরো পরিষ্কার বুঝতে পারবে।

মাধ্যমিক রামধনুর ক্ষেত্রে কিন্তু ব্যাপারটা হয় ঠিক উল্টো! ইমপ্যাক্ট প্যারামিটার বাড়ার সাথে-সাথে বিক্ষেপ কোণ প্রথমে বাড়ে এবং ১৩০° অতিক্রম করার পর কমতে শুরু করে। এক্ষেত্রে ১৩০° হল বিক্ষেপ কোণের সর্বোচ্চ মান।

এই যে বিক্ষেপ কোণের একটা সর্বনিম্ন মান আছে, ডেকার্টের এই পর্যবেক্ষণের গুরুত্বটা কতখানি সেটা বোঝার জন্য একটু কল্পনাশক্তি প্রয়োগ করা যাক। ধরো, আকাশের জলবিন্দুগুলি এমনভাবে আলোকরশ্মিদের বিক্ষেপণ ঘটাচ্ছে যাতে করে আকাশের সর্বত্রই ঔজ্জল্য একইরকম। তাহলে কি আদৌ রামধনু বলে কিছু থাকত? থাকত না! আবার বিক্ষেপ কোণের মান যদি ক্রমাগত কমতেই থাকত ইমপ্যাক্ট প্যারামিটার বাড়ার সাথে-সাথে, তাহলেও লাভের লাভ কিছু হত না। ইমপ্যাক্ট প্যারামিটার-এর অসংখ্য মানের জন্য অসংখ্য বিক্ষেপ কোণের মাঝে আমাদের রামধনু কোণ হারিয়ে যেত! বিক্ষেপ কোণের একটা সর্বনিম্ন মান থাকার ফলেই বিক্ষিপ্ত আলোকরশ্মিদের একটা বড় অংশ ওই বিশেষ কোণের আশেপাশে জড়ো হয়। কেন? নিচের ছবিটাতে আমি ইমপ্যাক্ট প্যারামিটারের সাথে বিক্ষেপ কোণের বিভিন্ন মানের একটা লেখচিত্র দিলাম।

ভাল করে খেয়াল কর – এই সর্বনিম্ন বিক্ষেপ কোণের কাছে ইমপ্যাক্ট প্যারামিটার পালটালেও বিক্ষেপ কোণ তেমন ভাবে পালটাচ্ছে না! অর্থাৎ, ইমপ্যাক্ট প্যারামিটার-এর সঙ্গে বিক্ষেপ কোণের পরিবর্তনের হার সব চাইতে কম বিক্ষেপ কোণের এই সর্বনিম্ন মানের জন্য। অতএব, জলকণার উপর বিভিন্ন আপতন কোণে পতিত অনেক রশ্মি ওই একই বিক্ষেপ কোণে ফিরে গিয়ে দর্শকের চোখে ধরা দেবে! তাই ১৩৭.৬° বিক্ষেপ কোণে লাল রঙের আলোর জটলা হবে, ১৩৮.৮° বিক্ষেপ কোণে হবে বেগুনির জটলা। ভিন্ন রঙের আলোর ভিন্ন বিক্ষেপ কোণে এই জটলাটাই হচ্ছে আমাদের রামধনু!

যেহেতু জলকণা থেকে ধাক্কা খেয়ে ফিরে আসা আলো রামধনু তৈরি করছে, তাহলে এবার বুঝলে তো, কেন রামধনু সূর্যের বিপরীত দিকে দেখা যায়? উপরের ছবিগুলির দিকে আরেকবার ভাল করে তাকালে বুঝবে যে সূর্যের আলোর দিকের সাথে মোটামুটি ৪২ ডিগ্রী কোণে প্রাথমিক রামধনু দেখা যায় – লাল থাকে উপরে, বেগুনি নিচে। মাধ্যমিক রামধনুর ক্ষেত্রে কিন্তু উলটো – বেগুনি উপরে, লাল নিচে!

উপরের লেখচিত্রের দিকে আবার তাকাও – ১৩০‍‍‍° ও ১৩৮°-র মাঝে কোন রামধনু (প্রাথমিক ও মাধ্যমিক) রশ্মির বিক্ষেপ কোণ নেই! অর্থাৎ, ওই কোণটুকুর মধ্যকার আকাশে কোনো বিক্ষিপ্ত আলো এসে পৌঁছবে না। এটাই আলেকজান্ডারের ডার্ক ব্যান্ড!

তাহলে তোমরা বুঝলে তো, যে রামধনুর রহস্য বেশ সহজ অঙ্ক কষেই বের করা যায়! আর একটা লক্ষ্য করার মত বিষয় হল, জলবিন্দুর আয়তনের উপর রামধনু কোণের মান নির্ভর করে না। থিওডোর যেমনটি দেখিয়েছিলেন – বিক্ষেপনের জ্যামিতি জলকণাদের জন্যও যা, জলভর্তি কাঁচের গোলকের জন্যও তাই! একটি জলকণা নিয়ে পরীক্ষা করা শক্ত, কিন্তু একটা কাঁচের গোলকের উপর উজ্জ্বল সাদা আলো ফেলে নিজেরাই রামধনু তৈরি করে দেখবে নাকি?

আবার যখন রামধনু উঠবে আকাশে, নতুন চোখে দেখবে! রামধনু সুন্দর, কিন্তু তার সৃষ্টি-রহস্য যে জানে তার চোখে সে আরো সুন্দরভাবে ধরা দেয়! আমাদের কথা কিন্তু এখনো ফুরোয়নি! আলোক রশ্মির জ্যামিতিক হিসেব কানুন দিয়ে রামধনুর অনেক সূক্ষ্ম কারুকার্য, যেমন অতিরিক্ত ধনু (supernumerary arcs, যার কথা তোমাদের আগের পর্বে বলেছিলাম) ব্যাখ্যা করা যায় না। এর ব্যাখা খুঁজতে হলে আমাদের আলোর তরঙ্গধর্ম নিয়ে আলোচনায় ঢুকতে হবে। সেই গল্প নিয়ে হাজির হব পরের পর্বে।

(প্রচ্ছদের ছবিটির উৎস)

তথ্যসূত্র: 

উপরের লেখাটির অনুপ্রেরণা ও আংশিকভাবে উৎস (আগ্রহী পাঠকদের জন্য) এখানে দেখুন।

—