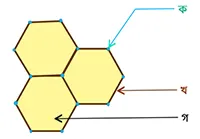
ফুটবলের নেপথ্যে বহুভূজ

ফুটবল বানানোর আধুনিক প্রযুক্তি আসার আগে ফুটবল সাধারণত কয়েকটি পঞ্চভূজ (pentagon) ও ষড়ভূজ (hexagon) সেলাই করেই তৈরি হত। সব চেয়ে প্রচলিত যে নকশা, তাতে থাকত 20টি ষড়ভূজ ও 12টি পঞ্চভূজ। কিন্তু এ ছাড়াও আরো কয়েক ধরণের নকশা বাজারে দেখা যেত। নিচে কয়েকটা উদাহরণ দেওয়া হলো।

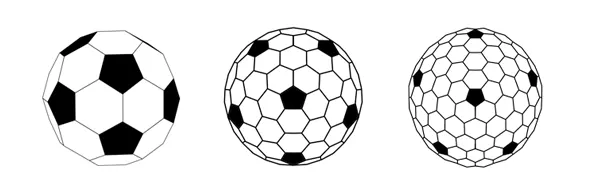
উপরের ছবিগুলো দেখে একজন পাঠক হয়ত এরই মধ্যেই আলাদা আলাদা ফুটবলে পঞ্চভূজের সংখ্যার মধ্যে কিছু মিল লক্ষ্য করে ফেলেছেন। মনে হচ্ছে ষড়ভূজের সংখ্যা যেন বিপুল পরিমাণে আলাদা, কিন্তু পঞ্চভূজগুলো একই সংখ্যায় উপস্থিত। এবার আপনি বলতেই পারেন যে আমি হয়ত এমন ছবি এখানে দিয়েছি যাতে এরকম একটি ভুল ধারণা মাথায় আসে। চলুন তাহলে এই বিষয় নিয়ে আরো কিছু গভীরে যাওয়া যাক, এবং দেখা যাক এই প্রশ্নের উত্তর খুঁজতে গণিত আদৌ কিছু সাহায্য করে কি না।

খুব বেশী গভীরে প্রবেশ করার আগে, চলুন আরেকটি অদ্ভুত সামঞ্জস্যের দিকে তাকাই। আমরা ধরে নেব পঞ্চভূজ ও ষড়ভূজের তৈরি ফুটবলটিতে মোট শীর্ষ বিন্দুর সংখ্যা , মোট বাহুর সংখ্যা ও মোট বহুভূজের তলের সংখ্যা । উপরের ফুটবলগুলোর ছবি একবার দেখলেই বোঝা যাচ্ছে যে প্রত্যেকটি শীর্ষ বিন্দু 3টি বহুভূজের অংশ এবং প্রত্যেক বাহু 2টি বহুভূজের অংশ। এই যুক্তির ভিত্তিতে সহজেই দেখা যাচ্ছে যে 20টি ষড়ভূজ ও 12টি পঞ্চভূজের ফুটবলে মোট শীর্ষ বিন্দুর সংখ্যা:

,

মোট বাহুর সংখ্যা:

ও মোট তলের সংখ্যা:

এই তিনটে সংখ্যার উপর একটু যোগবিয়োগ চালালে পাওয়া যাবে:

উপরের দ্বিতীয় ছবিটিতে দেখতে পাই যে , ও ; সুতরাং আবার পাওয়া গেল:

হঠাৎ এই “2” সংখ্যাটাকে কেমন যেন রহস্যময় লাগছে। এবার আমি যদি বলি ষড়ভূজ ও পঞ্চভূজ দিয়ে তৈরী প্রতিটি ফুটবলের ক্ষেত্রে

তাহলে এর সত্যতা নিয়ে নিশ্চয় প্রশ্ন উঠবে, কিন্তু আমরা এর সত্যতা প্রমাণ করব একটু বাদে। তার আগে একটু দেখে নি যে এই সমীকরণের সত্যতা ধরে নিলে আমরা কি পাই।

অয়লার সংখ্যা

চলুন একটি ফুটবলের কথা ধরা যাক যেটায়  সংখ্যক পঞ্চভূজ আছে ও  সংখ্যক ষড়ভূজ আছে। এরম একটি ফুটবলের মোট বহুভূজের তলের সংখ্যা

মোট শীর্ষ বিন্দুর সংখ্যা নির্ধারণ করার জন্যে আমাদের শুধু বুঝতে হবে যে প্রত্যেক পঞ্চভূজে 5টি ও ষড়ভূজে 6টি শীর্ষ বিন্দু আছে, এবং প্রত্যেক শীর্ষ বিন্দু 3টি বহুভূজের অংশ, তাই

,

যেহেতু প্রত্যেক বাহু 2টি বহুভূজের অংশ, একই ভাবে পাওয়া যাবে যে মোট বাহুর সংখ্যা

তাহলে আমাদের ওই শুরুর ধরে নেওয়াটা ঠিক হলে দাঁড়ায়:

এই ছোট্ট গণনার ফলেই আমরা পেয়ে যাচ্ছি যে কোন ফুটবল যদি ষড়ভূজ ও পঞ্চভূজ সেলাই করে তৈরি হয়, পঞ্চভূজের সংখ্যা কিন্তু 12টিতেই সীমিত, কমও নয়, বেশীও নয়।

অবশ্যই এই ফলাফল আমাদের অবাক করে দেয়, কিন্তু এর সত্যতার পিছনে লুকিয়ে আছে আমাদের নির্ধারণ করা সমীকরণ

এইটি হল জনপ্রিয় সুইস গণিতবিদ লিওনার্ড অয়েলারের (Leonhard Euler) দেওয়া এক উপপাদ্য। আমরা যতটা সহজে সম্ভব এর ব্যাখ্যা করার চেষ্টা করব। কিন্তু তার জন্য আমাদের একটি গোলকের (sphere) জ্যামিতির কিছু অংশ বুঝতে হবে। আমরা  সংখ্যাটিকে “অয়েলার সংখ্যা” বলবো এবং তাকে দিয়ে চিহ্নিত করবো।

একটি পৃষ্ঠতলের উপরিভাগে যদি আমরা কিছু বহুভূজ ব্যবহার করে সেলাই করি, প্রত্যেকটি আলাদা নকশা হবে সেই পৃষ্ঠতলের এক প্রকারের “ট্রায়াঙ্গুলেশান” (triangulation), এবং প্রত্যেক ট্রায়াঙ্গুলেশানের জন্য একটি অয়েলার সংখ্যা হয়। তাহলে বোঝা যাচ্ছে যে ফুটবলের নকশাগুলো আসলে এক এক ধরনের গোলকের ট্রায়াঙ্গুলেশান। আমরা যেটা ব্যাখ্যা করার চেষ্টা করব সেটা হল একটি পৃষ্ঠতলের প্রত্যেকটি ট্রায়াঙ্গুলেশানের অয়েলার সংখ্যা সমান।

বক্রতার খুঁটিনাটি

এবার গোলকের জ্যামিতিতে আসা যাক। গোলকের উপরিভাগ হল বক্র। যত কম তার ব্যাসার্ধ তত বেশি বক্র তার উপরিভাগ। এটা বোঝার একটি সহজ উপায় হলো এইরকম: ধরুন আপনি পৃথিবীর উপরিভাগে দাঁড়িয়ে আছেন, সেটি কিন্তু একটি সরল পৃষ্ঠতল মনে হয়। এর কারণ পৃথিবীর ব্যাসার্ধ এত বেশী যে সেটি অল্প পরিসরে একটি সমতল রূপ ধারণ করে।

এই বক্রতাকে সংখ্যায় ব্যক্ত করার জন্যে একটি গাণিতিক রাশি হচ্ছে , যাকে বলে গাউসিয়ান কারভেচার (Gaussian curvature)। এই নামকরণ বিশিষ্ট জার্মান গণিতবিদ ইয়হান কার্ল র্ফেড্রিক গাউসের (Johann Karl Friedrich Gauss) নামে। নীচের ছবিগুলো দেখলেই এই রাশিটার অর্থ পরিস্কার হয়ে যাবে। পৃষ্ঠতলের উপর একটি বিন্দু যদি মূলবিন্দুর (এখানে মূলবিন্দুর অর্থ হল origin (0,0,0)) থেকে দূরের দিকে বক্র হয়ে থাকে তার গাউসিয়ান কারভেচার ধনাত্মক (এর উদাহরণ হল গোলক)। যদি মূলবিন্দুর প্রতি বক্র হয়ে থাকে তার গাউসিয়ান কারভেচার ঋণাত্মক (এর উদাহরণ একটি hyperboloid)।

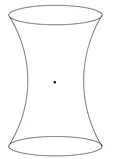
তাহলে দেখা যাচ্ছে যে -ব্যাসার্ধ গোলকের উপরিভাগে প্রত্যেকটি বিন্দুতে গাউসিয়ান কারভেচার ধনাত্মক। এবার এটা বার করা যায় যে প্রত্যেকটি বিন্দু -তে গাউসিয়ান কারভেচার

^[১]

গাউস ও বনেটের দেওয়া জনপ্রিয় একটি উপপাদ্য (Gauss-Bonnet Theorem) আছে, যেটা বলে যে

যেখানে একটি পৃষ্ঠতল ও হল সেই পৃষ্ঠতলের যে কোন ট্রায়াঙ্গুলেশানের অয়েলার সংখ্যা। অঙ্কটাকে ভাষায় বললে দাঁড়ায়: একটি পৃষ্ঠতলের উপরিভাগের উপর গাউসিয়ান কারভেচারের সমাকলন (integration) হল গুণিত সেই পৃষ্ঠতলের যে কোন ট্রায়াঙ্গুলেশানের অয়েলার সংখ্যা।

এই উপপাদ্য ব্যবহার করে সহজেই একটি গোলকের অয়েলার সংখ্যা বের করেতে পারি। আমরা জানি যে একটি -ব্যাসার্ধ বিশিষ্ট গোলকের উপরিভাগের ক্ষেত্রফল হচ্ছে , তাই

অতএব একটি -ব্যাসার্ধ গোলকের অয়েলার সংখ্যা:

অবশেষে বোঝা গেল যে আমরা যা যা অনুমান করে আমাদের মূল উদ্দেশ্যে পৌঁছেছিলাম সবেরই একটি গাণিতিক ভিত্তি আছে।

গাউস-বনেটের বাস্তব প্রয়োগ

গাউস ও বনেট উপপাদ্যের থেকে কিছু গুরুত্বপূর্ণ বিষয় বেরিয়ে আসে। এটা বোঝার জন্য একটি হাওয়া বের করা ফুটবলের ছবি দেখা যাক। স্বাভাবিক ভাবেই যত ধরণের বহুভূজ সেলাই করে একটি হাওয়া ভরা ফুটবল তৈরি হয়, একটি হাওয়া বের করা ফুটবলও ঠিক একই সংখ্যক বহুভূজ দিয়ে তৈরি হয়। কারণ, হাওয়া বার করে দিলেও বহুভূজের সংখ্যা তো আর পাল্টাবে না!

তার মানে একই ট্রায়াঙ্গুলেশান দুইয়ের জন্য প্রযোজ্য। অর্থাৎ একটি ফুটবলের অয়েলার সংখ্যা ফুটবলটিকে ফোলানোর বা চাপার উপর পালটায় না। এইরকম ধর্মকে গাণিতিক ভাষায় বলা হয় টোপোলজিকাল ইনভেরিয়েন্স (topological invariance)।

কিন্তু আপনি এই প্রশ্ন তুলতেই পারেন যে আমরা একটি ফুটবলের আকারের কোন পরিবর্তন ঘটালে তার উপরিভাগে কিছু বিন্দুর গাউসিয়ান কারভেচার (বা বক্রতার পরিমাপ) তো বদলাতে পারে। যেমন কিছু বিন্দুর গাউসিয়ান কারভেচার ধনাত্মক থেকে ঋণাত্মক হয়ে যেতে পারে। অবশ্যই ঠিক। কিন্তু যেটার পরিবর্তন হবে না সেটা হল পুরো উপরিভাগের উপর গাউসিয়ান কারভেচারের সমাকলন (integration)।

এটা অত্যন্ত জোরদার একটি ফলাফল। যারা বিদ্যালয়ের পরে কিছুটা গণিত চর্চা করেছেন, তারা হয়ত আরেকটু ভাল ব্যাপারটা বুঝতে পারবেন। গাউস বনেট উপপাদ্যের সমীকরণের বাম দিকটি হল একটি জ্যামিতিক বস্তু আর ডান দিকটি হল একটি topological বস্তু। এই দুই ভিন্ন ধারার মিলন ঘটাতে পেরেছে বলেই এই উপপাদ্যটা এতটা জনপ্রিয়।

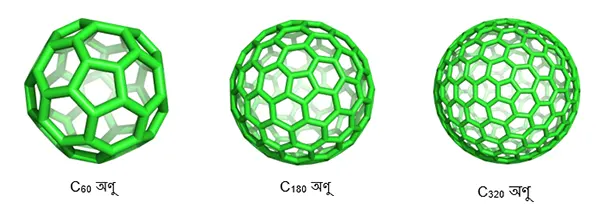
এই জ্যামিতিক প্রভাব শুধু ফুটবলেই সীমিত নয়। রসায়নের দুনিয়ায় একটি জনপ্রিয় অণুর উল্লেখ বহু জায়গায় পাওয়া যায়, যার নাম Buckminsterfullerene। এর একেকটা অণু 60টি কার্বন পরমাণু () দিয়ে তৈরি। এই অণুর জ্যামিতি লক্ষ্য করলে দেখা যাবে যে সেটিও একইরকম 20টি ষড়ভুজ ও 12টি পঞ্চভুজ দিয়ে তৈরি। আরো বহু প্রকারের fullerene অণুর সন্ধান বৈজ্ঞানিকরা পেয়েছেন, এবং দেখা যায় যে তারা প্রত্যেকেই একটি গোলকের বিভিন্ন ট্রায়াঙ্গুলেশান।

এই ফলাফল নিশ্চিতভাবে দেখায় যে একইরকম জ্যামিতি এই পৃথিবীর নানা নকশার সঙ্গে জড়িত। যদিও এই গভীর মিলন খুঁজতে গেলে গণিতজ্ঞদের বহু তাত্ত্বিক কাজকর্মের মধ্যে দিয়ে যেতে হয়, কিন্তু দিনের শেষে যখন সেই মিল খুঁজে পাওয়া যায়, তখন তার চেয়ে আনন্দের বিষয় আর কি আছে?

কভার ইমেজ : নির্মিতি মূলেয়

এই বিষয়ে আরো জানতে হলেঃ

[১] https://www.youtube.com/watch?v=gi-TBlh44gY এই ভিডিয়োতে গাউসিন কারচারের আরো কিছু প্রভাব জানা যাবে।

[২] আমরা জানি একটি ত্রিভুজের 3টি অন্তঃকোণের সমষ্টি 180 ডিগ্রি। কিন্তু একটি গোলকের উপরিভাগে একটি ত্রিভুজের 3টি অন্তঃকোণের সমষ্টি হয় 180 ডিগ্রির চেয়ে বেশী। এই ফলাফলের ভিত্তি আবার সেই গাউস বনেট উপপাদ্য। এই বিষয় ব্যাখ্যা করে “বিজ্ঞানে” অধ্যাপক স্বর্নেন্দু শীলের একটি লেখা আছে ^[২]। সেখানে ধনাত্মক ও ঋণাত্মক গাউসিয়ান কারভেচারের পৃষ্ঠতলের আরো কিছু জ্যামিতিক চরিত্রের উল্লেখ আছে।

রেফারেন্স:

[১] http://pi.math.cornell.edu/~bowman/curv.pdf (এখানে একটি -ব্যাসার্ধ গোলকের গাউসিয়ান কারভেচারের গণনা পাওয়া যাবে।)

[২] স্বর্নেন্দু শীল, জ্যামিতির গোড়ার কথা: এউক্লিড থেকে রীমান ৪ (https://bigyan.org.in/2016/04/04/elements-of-geometry-part-4/)