যে কোন ঘড়িতে একটা দোলক (oscillator) আর একটা গণক (counter) থাকে। একেক ধরণের ঘড়িতে একেক রকম দোলক থাকতে পারে। সে দোলক হতে পারে চলন (motion) ভিত্তিক, যেমন পৃথিবীর একপাক ঘোরা বা একটা যান্ত্রিক পেন্ডুলাম-এর দোলুনি। আবার কোনো চারিত্রিক পরিবর্তনও দোলকের কাজ করতে পারে, যেমন একটা স্ফটিক-এর (crystal) দৈর্ঘ্যে পরিবর্তন বা পরমাণুর ভিতর ইলেক্ট্রন-এর শক্তিস্তর পরিবর্তন। এসব ক্ষেত্রেই দোলকটার স্বভাব হলো, নির্দিষ্ট সময় পর পর তার অবস্থার পুনরাবৃত্তি হয় আর গণক সেই পুনরাবৃত্তির নির্ভুল হিসাব রাখে। চ্যুতিহীন দোলক এবং ত্রুটিহীন গণনার উপর একটা ঘড়ি কতটা ‘সঠিক’ এবং ‘স্থির’, তা নির্ভর করে। বিস্তারিত আলোচনার আগে এই দুটো বিষয়ে আমাদের স্বচ্ছ ধারণা থাকা আবশ্যক।
পরিমাপের স্থিরতা
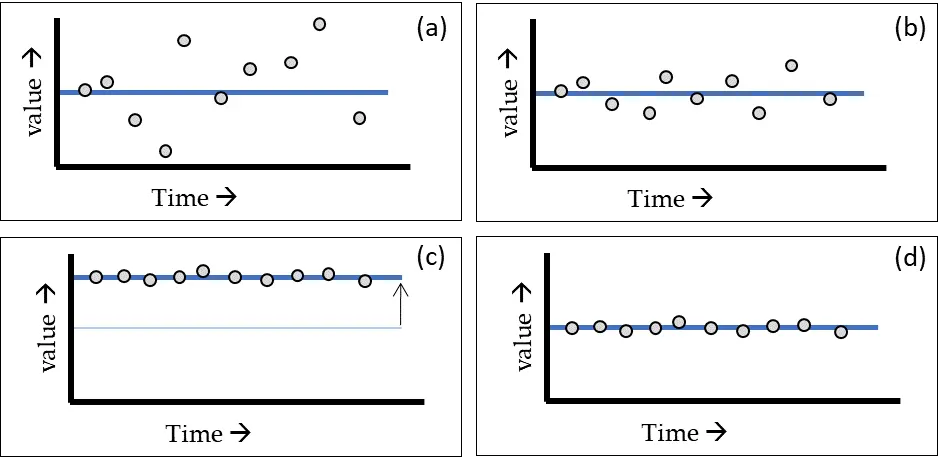
এখন ধর, তুমি একটা নির্দিষ্ট জিনিসের পরিমাপের দশটা করে মান পর্যায়ক্রমে লিপিবদ্ধ করেছ এবং তাদের একটা গ্রাফ বানিয়েছ। এখানে মোটামুটি চারটে সম্ভাবনা তৈরি হতে পারে (যেমন, চিত্র ১-এ দেখানো হয়েছে):
(ক) পরিমাপের মানগুলো আসল মানের থেকে দূরে ছড়িয়ে রয়েছে এবং আসল মানের সাথে তাদের কোনো পারস্পরিক সম্পর্ক নেই। এক্ষেত্রে পরিমাপটা বেঠিক এবং স্থিরতাহীন (inaccurate and unstable)।
(খ) পরিমাপের মানগুলো আসল মানের কাছাকাছি কিন্তু অনেকটা জায়গা জুড়ে ছড়িয়ে আছে। পরিমাপটা তখন সঠিক কিন্তু স্থিরতাহীন (accurate but unstable)।
(গ) পরিমাপের মানগুলো আসল মানের থেকে দূরে কিন্তু একে অপরের কাছাকাছি। এক্ষেত্রে পরিমাপটা বেঠিক কিন্তু স্থির (inaccurate but stable)।
(ঘ) পরিমাপের মানগুলো আসল মানের খুব কাছাকাছি এবং খুব বেশী ছড়িয়ে নেই। এরকম পরিমাপ সঠিক এবং স্থির (accurate and stable)। যে কোনো পরীক্ষাতেই চেষ্টা করা হয় নির্ভুল এবং স্থির পরিমাপ করার। কিন্তু বাস্তবে স্থিরতা এলেও পরিমাপটা আসল মান-এর থেকে একটু দূরে থাকে।
তবে পরিমাপগুলো স্থির হলে একটা সুবিধে আছে। প্রত্যেকবার মাপলে যদি একই বা কাছাকাছি মান পাওয়া যায়, তাহলে এই পরিমাপগুলোর গড় (average) নিলে সেই গড়টার একটা মানে থাকে। নইলে কিছু মান শূন্যের অনেক উপরে আর কিছু মান অনেক নিচে, এরকম হলে তার গড় মান শূন্য বলে লাভটা কি! যাইহোক, একবার সেই গড় মাপটা পেলে তার থেকে আসল মানটা বার করা সম্ভব। তার জন্য আগে থেকে জানতে হয় পরিমাপের সাথে আসলের তফাৎ-টা (offset) আসছে কোত্থেকে, যন্ত্রের কারণে নাকি পারিপার্শ্বিক কোনো প্রভাবের কারণে। এই তফাৎ-টা পারিপার্শ্বিক আর কোনো পরিবর্তন না হলে প্রত্যেক পরিমাপেই যে একই থাকবে এরকমটা আশা করা যায়, তাই একে বলা হয় systematics। তফাতের সূত্র জানলে কতটা তফাৎ হয় সেটাও আগে থেকে বার করা যায় এবং পরিমাপের গড় থেকে সেই তফাৎটা বাদ দিয়ে আসল মান-টা পাওয়া যায়। যদিও কি কারণে আসলের সাথে পরিমাপের তফাৎ হতে পারে আর কতটা হতে পারে, সেটা বার করার জন্য অনেক পরীক্ষা নিরীক্ষা আর চুলচেরা বিশ্লেষণের প্রয়োজন। এই ব্যাপারটা বেশ শ্রমসাদ্ধ, তাই পারমাণবিক ঘড়ি জাতীয় হাই-প্রিসিশন পরিমাপ (high precision measurement) সাধারণ গবেষণাগারের বেশিরভাগ সাধারণ পরিমাপের থেকে অনেকটাই আলাদা হয়।
পারমাণবিক ঘড়িতে কিসের দোলন মাপা হয়
একটা পরমাণুতে ইলেক্ট্রনগুলো বিশেষ কিছু শক্তিস্তরে (energy levels) বিচরণ করে। সবথেকে আলগাভাগে নিউক্লিয়াসের সাথে যুক্ত যে ইলেক্ট্রন বা ইলেক্ট্রনগুলো (valence electron), তাদের স্বাভাবিক অবস্থার থেকে আরো উচ্চ শক্তিতে পাঠানো যায়। এটাকে বলে পারমাণবিক স্থানান্তর (atomic transition)। উত্তেজিত ইলেক্ট্রনগুলো এমনিতে একটা সময় পর আবার স্বস্থানে ফেরত আসে, সময়টা নির্ভর করে উত্তেজিত অবস্থাটার পরমায়ুর (lifetime) উপর। ইলেক্ট্রন-এর এই উত্তেজনা এবং ফেরত আসা, এটা একটা বিশেষ কম্পাঙ্কে (frequency) হয়, যেটা স্বাভাবিকভাবে অত্যন্ত নির্দিষ্ট এবং স্থির। এই সুনির্দিষ্ট কম্পাঙ্কের কারণে এটা দোলকের কাজ করতে পারে। এর আগে যেসব দোলনের (periodic motion) কথা বলা হয়েছে, তাদের কম্পাঙ্ক পরিমাপের তুলনায় এই রশ্মির কম্পাঙ্ক পরিমাপ অনেক বেশী নির্ভরযোগ্য। কম্পাঙ্কের মানটা এতটা স্থির কারণ সেটা আসলে ওই দুটো অবস্থার শক্তির তফাৎকে (energy difference) চিহ্নিত করছে। এই তফাৎটাকে প্লাঙ্ক ধ্রুবক (Planck’s constant) দিয়ে ভাগ করলেই ওই কম্পাঙ্কের মানটা বেরিয়ে আসে। এই যে শক্তির তফাৎ, এটা কিন্তু ওই পরমাণুর একটা মৌলিক চরিত্র, এবং অজানা কোনো পারিপার্শ্বিক কারণে সেটা এদিকওদিক হয়না।
অন্যভাবে বললে, পারমাণবিক ঘড়িতে দুটো বিশেষ অবস্থার মধ্যে পারমাণবিক স্থানান্তর (atomic transition) প্রক্রিয়াটা দোলকের কাজ করছে। ঘড়ির মধ্যে সেই দোলকের কম্পাঙ্কটাকেই মাপা হয় অত্যাধুনিক যন্ত্রের সাহায্যে। কম্পাঙ্কটা বলে, কি হারে ইলেক্ট্রন ওই দুটো অবস্থার মধ্যে যাতায়াত করছে। সময়ের এককের সংজ্ঞাটা মানলে সিজিয়াম পরমাণুর সর্বনিম্ন দুটো হাইপারফাইন শক্তিস্তরের মধ্যে ৯, ১৯২, ৬৩১, ৭৭০ বার যাতায়াতের জন্য কতটা সময় লাগছে, সেইটা থেকে “এক সেকেন্ড” সময়টা পাওয়া যায়। অর্থাৎ, ঘড়িটাকে পারমাণবিক স্থানান্তরের কম্পাঙ্কে লক করে স্থানান্তরগুলো নামাতে পারলেই সময় মাপাও হয়ে গেল। পারমাণবিক ঘড়িগুলোকে সেই অর্থে সময় পরিমাপের স্ট্যান্ডার্ড না বলে কম্পাঙ্ক পরিমাপের স্ট্যান্ডার্ড-ও বলা যায়।
বিশেষ কিছু পারমাণবিক স্থানান্তরকেই ঘড়ির কাজে লাগানো যায়। এই স্থানান্তরগুলোর জন্য ১০৯ Hz থেকে ১০১৪ Hz-এর রশ্মির প্রয়োজন হতে পারে, অর্থাৎ, সেই রশ্মির তরঙ্গদৈর্ঘ্য (wavelength) মাইক্রোওয়েভ থেকে দৃশ্যমান আলোর তরঙ্গের মধ্যে পড়তে পারে। যত বেশী সেই রশ্মির কম্পাঙ্ক, তত একটা দোলন গুনতে ভুল করলে গোটা পরিমাপে তার প্রভাবটা কম হবে। সুতরাং ১০১৪ Hz-এর অপটিক্যাল ঘড়ি (optical clock) ১০৯ Hz-এর মাইক্রোওয়েভ ঘড়ির (microwave clock) তুলনায় বেশী সঠিক পরিমাপ দিয়ে থাকে। পারমাণবিক ঘড়ি এই কম্পাঙ্কটাকেই যতটা সম্ভব সূক্ষ্মভাবে মাপে। সঠিকতা আর স্থিরতা বাড়াতে সেই মাপের পর আরো পোস্ট প্রসেসিং (post processing) করতে হয়,যাতে কম্পাঙ্কের পরিমাপ সূক্ষ্ম থেকে সূক্ষ্মতর পর্যায়ে পৌঁছায়।
সবথেকে সঠিক পারমাণবিক ঘড়ি ঠিক কতটা সঠিক? সহজভাবে বললে, ধরা যাক, এরকম একটা ঘড়ি আমাদের বিশ্বব্রম্ভান্ডের শুরু থেকে চলছে, অর্থাৎ ১৩৮০ কোটি বছর আগে থেকে। তাহলে বর্তমানে এসে দেখা যাবে, তাতে এক সেকেন্ডের হেরফের হয়েছে। এটা খানিকটা গোটা পৃথিবীতে কতটা জল আছে, সেইটা মাপতে গিয়ে এক কিউবিক মিটার ভুল হওয়ার মতো।
এবার দেখা যাক, আজকের দিনের সময় পরিমাপের মেরুদন্ড, অর্থাৎ পারমাণবিক ঘড়ি, কিভাবে কাজ করে।
পারমাণবিক ঘড়ির নানা প্রকার
পারমাণবিক ঘড়ি কোন কম্পাঙ্কে চলছে, তার ভিত্তিতে এদের দুটো শ্রেণীতে ভাগ করা হয় – মাইক্রোওয়েভ আর অপটিক্যাল ঘড়ি। দু’ধরণের ঘড়িই একই নীতিতে চলে। কোন পরমাণু নিয়ে এবং তাদের কোন দুটো শক্তিস্তরের মধ্যেকার কম্পাঙ্ক নিয়ে কাজ করা হচ্ছে, সেখানেই ঘড়িগুলোর তফাৎ। এছাড়াও এদের চালাতে এবং পরিমাপের সূক্ষ্মতা বাড়াতে যেসব উপায় ব্যবহার হয়, সেগুলোতেও তফাৎ থাকে। যেমন, স্বাভাবিক তাপমাত্রার থেকে লক্ষগুণ কম তাপমাত্রায় গিয়ে ঘড়ির সঠিকতা মোটামুটি লক্ষগুণ বাড়িয়ে দেওয়া যায়। অবশ্যই অতটা ঠান্ডা পরমাণু নিয়ে কাজ করতে হলে তার প্রযুক্তিও আর এক থাকে না। নতুন, উন্নততর, জটিলতর প্রযুক্তির আশ্রয় নিতে হয়।
নিচের টেবিলে বিভিন্ন ধরণের ঘড়ি এবং সাধারণত তাদের সঠিকতা কিরকম হয়, সেই মানগুলো দেওয়া হলো। হাইড্রোজেন-মেসার (Hydrogen maser বা H-maser), রুবিডিয়াম ঘড়ি (rubidium clock বা Rb-clock) এবং সিজিয়াম ঘড়ির (Cesium clock বা Cs-clock) পরমাণুগুলো প্রায় ঘরের তাপমাত্রায় কাজ করে। এই ঘড়িগুলো কয়েক দশক আগেই তৈরি হয়েছে এবং এখন বাজারেও কিনতে পাওয়া যায়।
তবে এর থেকেও উন্নত ঘড়ি হয়। যেমন, মাইক্রোওয়েভ ফোয়ারা ঘড়ি (microwave fountain clock)। এগুলো লেজার রশ্মি দিয়ে সিজিয়াম বা রুবিডিয়াম পরমাণু ঠাণ্ডা এবং আবদ্ধ করে (cooling and trapping technique), তারপর সেগুলোকে ব্যবহার করে। সিজিয়াম ফোয়ারা ঘড়ি (Cesium fountain clock) বর্তমানে পৃথিবীর কয়েকটা দেশেই রয়েছে, যেমন, অ্যামেরিকা, ফ্রান্স, ইংল্যান্ড, ইতালি, জার্মানি ও জাপান ইত্যাদি [১]। পারমাণবিক ঘড়িগুলোর মধ্যে সবথেকে সঠিক সময় দেয় অপটিক্যাল ঘড়ি। তবে হাতেগোনা কয়েকটা উন্নত দেশেই এটা রয়েছে। এই ফোয়ারা বা অপটিকাল ঘড়িগুলোকে পরীক্ষাগারে সযত্নে ধাপে ধাপে তৈরি করতে হয়, এখনও এগুলো বাজারে কিনতে পাওয়া যায় না।
এই ধরণের ঘড়ি চালু রাখতে যে প্রযুক্তি লাগে, সেরকম প্রযুক্তি দেশের মধ্যেই তৈরি করতে পারা উচিত। নয়তো অত্যাধুনিক সব প্রযুক্তির চালাতে যেরকম সঠিক সময় নির্ধারণ প্রয়োজন, তার জন্য বাইরের উপর নির্ভরশীল হয়ে থাকতে হবে। শুধু প্রযুক্তি না, মৌলিক বিজ্ঞান গবেষণাতেও এই ধরণের ঘড়ির অপরিসীম গুরুত্ব রয়েছে। তাই, ভারত সহ অন্যান্য উন্নয়নশীল দেশ চেষ্টা করছে নিজেরাই এরকম ঘড়ি বানাতে। এর প্রয়োগ হবে সর্বত্র, লক্ষ্যে মিসাইল পাঠানো বা নজরদারি থেকে শুরু করে বিমানচালনা বা আধুনিক যোগাযোগ ব্যবস্থায়।
| দোলক এবং কোন কম্পাঙ্কে চলে | সঠিকতা | স্থিরতা প্রতি সেকেন্ড |
| H-Maser ১ ৪২০ ৪০৫ ৭৫২ Hz | ১০–১৩ | ১০–১৩ |
| Rb-clock ৬ ৮৩৪ ৬৮২ ৬০৮ Hz | ১০–১১ | ১০–১১ |
| Cs-clock ৯ ১৯২ ৬৩১ ৭৭০ Hz | ১০–১৪ | ১০–১২ |
| Cs-fountain ৯ ১৯২ ৬৩১ ৭৭০ Hz | ১০-১৬ | ১০-১২ |
| Optical clock ১০১৪ Hz | ১০–১৮ | ১০–১৬ |
এস আই নিয়মে ‘সেকেন্ড’-এর সংজ্ঞা হ’ল এইরকম: শূন্য কেলভিন তাপমাত্রায় অনুত্তেজিত অবস্থায় একটা সিজিয়াম (১৩৩Cs) পরমাণুর দুটো হাইপারফাইন শক্তিস্তরের (hyperfine state) মধ্যে ৯ ১৯২ ৬৩১ ৭৭০ বার যাওয়া আসা করতে যতটা সময় লাগে। এই সংজ্ঞার মধ্যেই সিজিয়াম ফোয়ারা ঘড়িকে সময়ের মানদণ্ড হিসাবে ধরা রয়েছে (যেহেতু তার মধ্যে সিজিয়াম পরমাণুকে প্রায় শূন্য কেলভিন তাপমাত্রায় ঠান্ডা করা হয়)। অপটিকাল পারমাণবিক ঘড়িগুলো সাধারণত এর তুলনায় কমপক্ষে ১০০গুণ বেশী সঠিক। কিন্তু সেকেন্ড-এর সংজ্ঞা এখনো নতুন করে তার ভিত্তিতে তৈরি করা হয়নি। ২০২৬ নাগাদ হবে আশা করা যায়।
উৎসাহী পাঠকদের জন্য লেখার শেষে সময় গণনার একটা কালানুক্রমিক ইতিহাস দেওয়া হলো। আপাতত দেখা যাক, সিজিয়াম ফোয়ারা ঘড়ি (Cs Fountain Clock) কিভাবে কাজ করে।
সিজিয়াম ফোয়ারা ঘড়িতে (Cs Fountain Clock) ফোয়ারাটা কিসের
প্রথমে বোঝা যাক, এই ঘড়ির নামটাতে পারমাণবিক “ফোয়ারা” (atomic “fountain”) আছে কেন। জলের ফোয়ারা, যেটা পার্ক জাতীয় জায়গায় দেখা যায়, তাতে জলের তোর ছিটকে উপরের দিকে যায় এবং একটা উচ্চতায় পৌঁছে অভিকর্ষের (gravity) কারণে আবার নিচের দিকে ফেরত আসে। এই উপর নিচ করার সময় জলের ফোঁটাগুলো কিছুটা ছড়িয়ে পড়ে, ফলে জলের ফোয়ারাকে ওরকম সুন্দর দেখতে লাগে। সিজিয়াম ফোয়ারা ঘড়িতে জলের বদলে সিজিয়াম পরমাণুর একটা সমষ্টি একইরকম পথ অনুসরণ করে এবং সেই জন্যই এর নাম সিজিয়াম ফোয়ারা।
তবে জলের ফোয়ারাতে জল তোরে ছাড়লেই হলো। এখানে পরমাণুগুলোকে ফোয়ারার রূপ দেওয়ার আগে একটা জটিল পদ্ধতি মেনে বিশেষ অবস্থায় প্রস্তুত করতে হয়। যেমন, পুরো কাজটা একটা সীল করা প্রায় বায়ুশূন্য স্থানে (vacuum sealed) করতে হয়। সেখানে বায়ুচাপ হয় সাধারণ বায়ুমণ্ডলের চাপের তুলনায় ১০–১২ গুণ কম (১০–৯ মিলিবার)। এটা করতে হয় যাতে সিজিয়াম পরমাণুগুলো নিজেদের মধ্যে বা অন্যান্য অণু পরমাণুর সাথে সংঘাত এড়িয়ে যেতে পারে। নইলে কম শক্তির সিজিয়াম পরমাণুগুলো সংঘাতের ফলে শক্তি সঞ্চয় করবে এবং যেমনখুশি গতি পাওয়ার ফলে এই সিজিয়াম ফোয়ারা ঘড়িতে কোনো কাজে আসবে না।
প্রথমে একতাল সিজিয়াম ধাতুকে তার গলনাঙ্কের (২৮.৫ ডিগ্রি সেন্টিগ্রেড) থেকে বেশী তাপমাত্রায় উত্তপ্ত করা হয়। এর ফলে সিজিয়ামের স্তুপ থেকে একেকটা পরমাণু ছিটকে বেড়িয়ে আসে। তাপমাত্রার কারণে তাদের শুরুতে একটা গতিশক্তি (kinetic energy) থাকে। সেই গতি ম্যাক্সয়েল-বোল্টজম্যান-এর সূত্র (Maxwell-Boltzmann statistics) অনুযায়ী শূন্য থেকে অসীম সবই হতে পারে। এই পরমাণুগুলোকে উপরদিকে যেতে দিলে এরা একেকজন একেকটা উচ্চতায় যাবে। এরকম একটা ছন্নছাড়া পরমাণুর দলকে ঘড়ির কাজে লাগানো যায়না। তাই, পরমাণুগুলোকে বার করার পর তাদের একত্র করে প্রায় শূন্য তাপমাত্রায় নিয়ে যাওয়া হয়। এর জন্য জটিল লেজার কুলিং (laser cooling) এবং ম্যাগনেটো-অপটিকাল ট্র্যাপিং (Magneto Optical Trapping বা MOT) পদ্ধতি ব্যবহার করা হয়ে থাকে।
লেজার দিয়ে ঠাণ্ডা করা
লেজার দিয়ে যে ঠাণ্ডা করা যায়, সেইটা ১৯৭৫ সালে দুটো দল আলাদা করে দেখায়, টি. ডবলু. হান্স (T. W. Hansch) ও এ. এল. শাওলো (A. L. Schawlow) এবং ডি. ওয়াইনল্যান্ড (D. Wineland) ও এইচ. ডেহমেল্ট (H. Dehmelt)। এই চার জন বিজ্ঞানীই নোবেল পেয়েছেন যথাক্রমে ২০০৫, ১৯৮১, ২০১২ এবং ১৯৮৯ সালে, কিন্তু লেজার দিয়ে ঠাণ্ডা করার উপায় বাৎলানোর জন্য নয়। সেই নোবেলটা গেছিলো ১৯৯৭ সালে স্টিভ চু (Steven Chu), ক্লাউডে কোহেন-তান্নাওজি (Claude Cohen-Tannoudji) এবং উইলিয়াম ডি. ফিলিপস (William D. Philips) এই তিন বিজ্ঞানীর কাছে। তারা লেজার দিয়ে পরমাণুর গতি নিয়ন্ত্রণ করে তাদের আবদ্ধ করার পদ্ধতি আবিষ্কার করেছিলেন।
লেজার কুলিং ও ট্র্যাপিং (laser cooling and trapping) পদ্ধতি নামটা থেকেই অনেকটা আঁচ করা যায়। লেজার দিয়ে পরমাণুর তাপজনিত শক্তি কমিয়ে দেওয়া হয়। প্রায় শূন্য তাপমাত্রায় যাওয়ার ফলে পরমাণুগুলোর গতিও প্রায় শূন্য হয়ে যায়। ফলে আগে যে অনেকরকম গতির সম্ভাবনা ছিল, সেইটা আর থাকে না। আর ম্যাগনেটো অপটিকাল ট্র্যাপ (Magneto Optical Trap বা MOT) প্রায় একশো কোটি পরমাণুকে এক মিলিমিটার ব্যাসের গোলকের আয়তনে কয়েদ করে ফেলে।
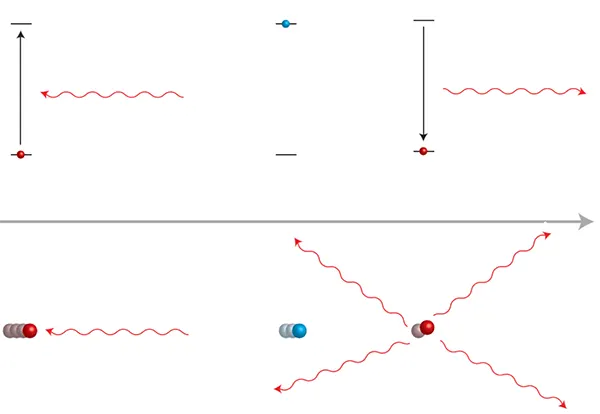
এই অব্দি শুনে যে প্রশ্নটা মাথায় আসে সেটা হলো, লেজার দিয়ে ঠান্ডা? এ আবার কেমন কথা? লেজার কিভাবে একটা পরমাণুর শক্তি কমাতে পারে? অবশ্যই একটা আলোককণা একটা পরমাণুকে উত্তেজিত করে থাকে, তবে সেটাই শেষ কথা নয়। কিছুটা সময় পর সেই পরমাণু আবার শুরুর অবস্থায় ফিরে আসে এবং শক্তি সংরক্ষণের (conservation of energy) ফলে একটা আলোককণা ছেড়ে দিয়ে। এই ঘটনাটাকে বলে ফ্লুওরেসেন্স (fluorescence)। শক্তি সংরক্ষণের (conservation of energy) ফলে পরমাণুটার শক্তি একই থেকে যায়। অতএব এইভাবে পরমাণু ঠান্ডা হতে পারেনা।
লেজারে যে ব্যাপারটা গুরুত্বপূর্ণ সেটা হলো, আলোককণাগুলোর গতি সব একই দিকে (spatial coherence)। এই ব্যাপারটা কিভাবে একটা পরমাণুর শক্তি কমাতে কাজে লাগানো যায়, সেটা নিচে চিত্র ২-এ দেখানো হলো। পরমাণুগুলো শোষণের সময় একই দিকে ধাবমান লক্ষ লক্ষ আলোককণাকে শুষে নেয় তবে ছাড়ার সময় সেগুলোকে দিগ্বিদিক নির্বিশেষে সবদিকে ছাড়ে। যেহেতু সমস্ত ফ্লুওরেসেন্স আলোককণাগুলোর গড় গতিবেগ শূন্য, মোটের উপর লেজারের আলোককণার শক্তিটা এখন পরমাণুর মধ্যে চালান হয়ে গেছে। চালান হওয়া গতিবেগটা যদি পরমাণুর নিজের গতিবেগের উল্টো দিকে হয়, তাহলে পরমাণুগুলোর গতি কমে আসবে, এবং পারতপক্ষে এই গতি কমে আসাটা হচ্ছে লেজারের মাধ্যমে শক্তিপ্রয়োগের ফলে। ব্যাস, হয়ে গেল লেজার দিয়ে ঠান্ডা! তিনটে সমকোণীয় (orthogonal) দিকে এইরকম লেজার পাঠাতে হয়, যাতে কোনদিকেই আর পরমাণুর গতি না থাকে। একেকটা দিকে একজোড়া বিপরীতমুখী লেজার তাক করতে হয় যাতে তাদের মাঝে একটাই জায়গা থাকে যেখানে পরমাণুগুলো শান্ত হয়ে থাকতে পারে। বিপরীতমুখী লেজার না পাঠিয়ে একটাই লেজার পাঠালে পরমাণু সেই লেজার-এর আলোককণার ঠ্যালায় ক্রমাগত চলতেই থাকবে, আর থামবে না।
পরমাণুদের কয়েদ করা
শুধু লেজার দিয়ে ঠান্ডা করাই যথেষ্ট নয়। পরমাণুগুলোকে ব্যবহারের উপযোগী করতে তাদের বন্দী করতে হয় একটা ছোট্ট জায়গার মধ্যে। এর জন্য একটা বল চাই যেটার মান জায়গাবিশেষে আলাদা হবে (spatially dependent force)। যেই পরমাণুগুলো তাদের বন্দী অবস্থা থেকে বেরোতে চেষ্টা করবে, তারা প্রয়োজনীয় মাপের বল অনুভব করবে এবং ধাক্কা খেয়ে ফেরত আসতে বাধ্য হবে। এর ফলে পরমাণুগুলো ঘাপটি মেরে বসে থাকবে এমন একটা জায়গায় যেখানে সেই বলজনিত শক্তি সবথেকে কম। এটাকেই পোশাকি ভাষায় বলে ফাঁদের কেন্দ্র (trap center)।
এই ধরণের বল সৃষ্টি করা হয় লেজার এবং চৌম্বক ক্ষেত্রের (magnetic field) সম্মিলিত প্রয়াসে। চৌম্বক ক্ষেত্রটা সর্বত্র এক নয়, সেটা ফাঁদের কেন্দ্রতে ভ্যানিশ হয়ে যায় এবং সেখান থেকে চারিদিকে এর মান রৈখিকভাবে (linearly) বাড়তে থাকে। চৌম্বক ক্ষেত্র-এর একটা দিক আছে, এক্ষেত্রে সেটা ফাঁদের কেন্দ্র থেকে উভয় দিকে বিপরীত মুখে কাজ করে। এই চৌম্বক ক্ষেত্রের প্রভাব এমন হয় যে সেটা সবসময় পরমাণুটাকে কেন্দ্রের দিকে পাঠাতে চেষ্টা করে। (পরমাণুর নিজস্ব একটা চৌম্বক ভ্রামক (magnetic moment) থাকে, সেইজন্যেই এরকম চৌম্বক ক্ষেত্রের প্রভাব সে অনুভব করে। এটাকে বিজ্ঞান-এর ভাষায় বলে জিমান ইফেক্ট – Zeeman effect। )
এই পদ্ধতিটার নাম ম্যাগনেটো-অপটিকাল ট্র্যাপিং (Magneto Optical Trapping বা সংক্ষেপে MOT), কারণ লেজার-এর আলো আর চৌম্বক ক্ষেত্রের ফাঁদ, দুইয়ে মিলে পরমাণুগুলোকে বন্দী করা হচ্ছে।
ঠান্ডা পরমাণুর সাথে মাইক্রোওয়েভের ক্রিয়া এবং শেষে কম্পাঙ্ক পরিমাপ
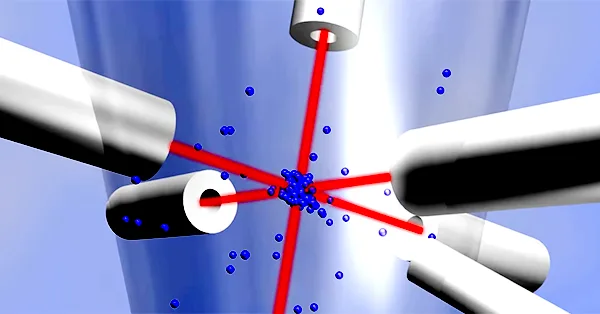
এইভাবে কিছু নোবেলজয়ী গবেষণার হাত ধরে একটা ঠান্ডা পরমাণুর সমষ্টিকে একটা ফাঁদের মধ্যে একত্র করা হলো। নিচের ছবিতে এইটা ঘড়ির স্টেজ (a) বলে চিহ্নিত করা হয়েছে। এখান থেকে শুরু করেই তৈরি হয় পরমাণুর ফোয়ারা।
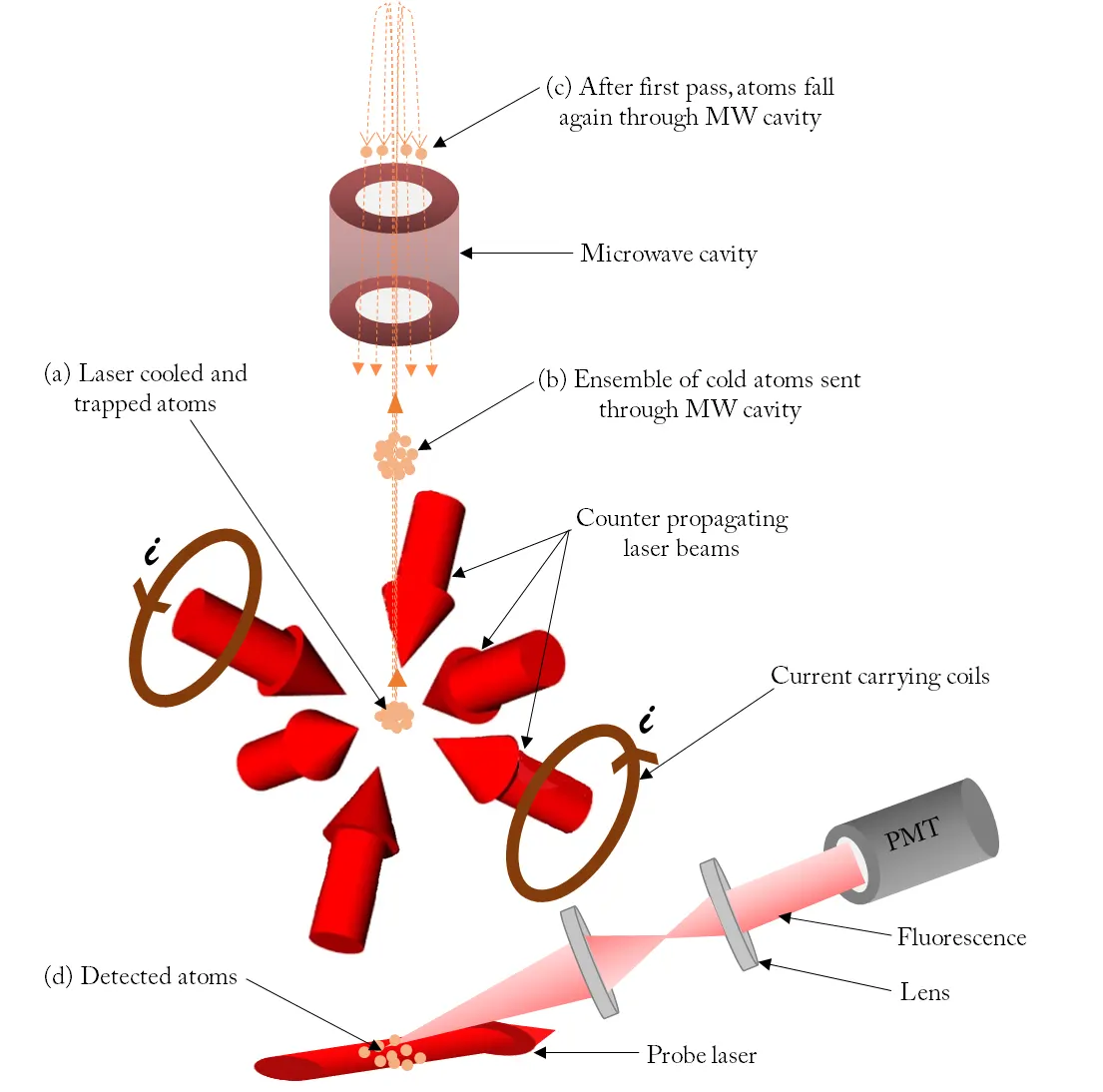
উপরের ছবিতে স্টেজ (b)-তে দেখানো হয়েছে। যেহেতু এখন আর ফাঁদটা নেই, এই যাত্রাপথে জমাটবাঁধা পরমাণুগুলো একে অপরের থেকে একটু দূরে সরে গিয়ে গোটা ব্যাপারটাকে একটা ফোয়ারার রূপ দেয়। যদিও সেই ফোয়ারাটা খুব বিস্তৃত হয়না কারণ শুরুর পরমাণুগুলোর প্রায় কোনো গতিশক্তিই ছিল না। এর ফলে পরমাণুগুলো যখন মাধ্যাকর্ষণের টানে একটা উচ্চতায় পৌঁছে আবার ফেরত আসে, সেগুলো তখনও ওই মাইক্রোওয়েভ গহ্বরের মধ্যে দিয়েই ফেরত যায়। তারা কিন্তু এতটাও ছড়িয়ে যায়নি যে গহ্বরের চৌহদ্দির বাইরে গিয়ে পড়বে।
অর্থাৎ একই মাইক্রোওয়েভ গহ্বর দিয়ে পরমাণুগুলো দুবার যায়। এই মাইক্রোওয়েভের কম্পাঙ্ক যদি সিজিয়াম পরমাণুর দুটো হাইপারফাইন স্তরের স্থানান্তর কম্পাঙ্কের (transition frequency) সাথে মিলে যায়, তখন সেটা সিজিয়াম পরমাণুগুলোকে একটা শক্তি স্তর থেকে আরেকটাতে স্থানান্তরিত করতে পারবে। যেহেতু মাইক্রোওয়েভ গহ্বরটা পরমাণুর যাতায়াতের পথে, তাই এক্ষেত্রে দুবার পরমাণুগুলো এই মাইক্রোওয়েভের দ্বারা প্রভাবিত হবে। দুবার যাতায়াতের ফলে কিভাবে পরিমাপটা আরো সূক্ষ্মতর হয়, সেটা পরে বলা হয়েছে।
আয়োজনটার একদম নিচে একটা ব্যবস্থা থাকে, যেটা ফেরত আসা পরমাণুগুলোর কতগুলো উত্তেজিত হয়েছে, সেইটা মাপে। ছবিতে এইটা স্টেজ (d)। মাইক্রোওয়েভ-টাকে যদি সঠিক কম্পাঙ্কে লক করা যায়, তখন এই উত্তেজিত হওয়া পরমাণুর সংখ্যাটা সবথেকে বেশী হবে। যে কম্পাঙ্কে এই সংখ্যাটা সর্বোচ্চ হবে, সেই কম্পাঙ্কটাই পড়ে ফেললেই কাজ শেষ। কম্পাঙ্কের পরিবর্তনের সাথে উত্তেজিত পরমাণুর সংখ্যাটা মাপলে খানিকটা নিচের ছবির মতো এইরকম একটা গ্রাফ পাওয়া যাবে। আপাতত গ্রাফে বড় পাহাড়টা দেখো। ওর চূড়াটা হলো কম্পাঙ্কের পরিমাপ আর দৈর্ঘ্য হলো সেই পরিমাপের বিস্তৃতি (এই বিস্তৃতিটা একটা ম্যাক্সওয়েল-বোল্টজমান বিন্যাস অনুসরণ করে)। দেখতেই পাচ্ছো, বিস্তৃতিটা অনেকটা। কিভাবে সেটা কমিয়ে ওই সরু পাহাড়ের দৈর্ঘ্যে নিয়ে যাওয়া হয়, সেটাই এর পর বলা হবে।
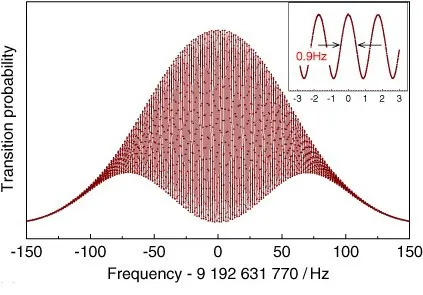
পরিমাপটা কিভাবে আরো সূক্ষ্ম (precise) করা যায়
উপরের ছবিতে গ্রাফের চূড়া যেখানে, সেই কম্পাঙ্কটা পড়ে ফেললেই সিজিয়াম পরমাণুর দুটো স্তরের মধ্যে স্থানান্তর কম্পাঙ্ক (transition frequency) পাওয়া যায়। কিন্তু ওই চূড়ার দৈর্ঘ্যটা বেশ বড় (ওটা আসলে একটা ম্যাক্সওয়েল-বোল্টজম্যান চূড়ার বিস্তার)। অর্থাৎ, পরিমাপে কতটা ভুল থাকতে পারে, সেইটা বেশ বড়। এইটা কমাতে যা করা হয়, সেই নিয়ে একটু বলি।
উপর নিচ যাতায়াতের সময় দুবারই পরমাণুগুলো একই কম্পাঙ্কের মাইক্রোওয়েভ-এর সাথে আন্তঃক্রিয়া (interaction) করে বটে, কিন্তু সেই দুটো আন্তঃক্রিয়ার মধ্যে একটা সময়ের তফাৎ থাকে। এই সময়ের তফাৎ-টা পরমাণুগুলোর কাছে মাইক্রোওয়েভের অবস্থার একটা তফাৎ (phase difference) হিসেবে ধরা দেয়। যেমন, উপরদিকে যাত্রার সময় যদি পরমাণুগুলো মাইক্রোওয়েভ তরঙ্গের একটা চড়াই দেখে, তো নিচে যাওয়ার সময় হয়তো উৎরাই দেখলো। কতটা অবস্থার তফাৎ হলো, সেটা দুটো আন্তঃক্রিয়ার মধ্যে একটা সময়ের তফাতের উপর নির্ভর করে, তাই বিভিন্ন পরমাণুর আলাদা গতিবেগের ফলে সেই তফাৎটাও আলাদা হয়। এই অবস্থার তফাতের কারণে একটা ঘটনা ঘটে, যাকে বলে তরঙ্গ ব্যতিচার (interference of waves)।
এই ঘটনাটা কিভাবে হয়, সেই বিবরণে না গিয়ে, শুধু এটুকুই বলা যায়, এই ব্যাতিচারের ফলে আগের ম্যাক্সওয়েল-বোল্টজমান বিন্যাসটা অনেকগুলো সূক্ষ্মভাগে বিভাজিত হয়। যে চূড়াটা হয়তো ১০০Hz সূক্ষ্মতায় মাপা যাচ্ছিলো, সেটা এখন ১Hz সূক্ষ্মতায় মাপা যায়। চিত্র ৪-এ বড় চূড়াটার ভিতর সরুসরু চূড়াগুলো দেখো।
সূক্ষ্মতা বাড়ানোর এই পদ্ধতিটাকে বলে র্যামসি স্পেক্ট্রোস্কোপি (Ramsey spectroscopy)। এই নামটা দেওয়া হয়েছে N F Ramsey-র নামে, যিনি এই পদ্ধতি আবিষ্কারের জন্য ১৯৮৯-এ নোবেল পুরষ্কার পেয়েছিলেন।
এক কথায় বললে, যখন মাইক্রোওয়েভ গহ্বরে আলোর কম্পাঙ্ক অনুরনণ (resonance) সৃষ্টি করে, অর্থাৎ সবথেকে বেশি পরমাণুকে উত্তেজিত করে, সেই অবস্থায় এই র্যামসি স্পেক্ট্রোস্কোপি পদ্ধতি ব্যবহার করলে সবথেকে সূক্ষ্ম কম্পাঙ্কের পরিমাপ পাওয়া যায়। এইভাবে, সিজিয়ামের স্থানান্তর কম্পাঙ্ক (transition frequency), যেটার মান ৯, ১৯২, ৬৩১, ৭৭০ Hz, সেইটা ১ Hz-এর থেকেও বেশী সূক্ষ্মতার সাথে মাপা যায়। এই সূক্ষ্মতার কারণেই সিজিয়াম ফোয়ারা ঘড়িকে কম্পাঙ্ক পরিমাপের (এবং সেই থেকে সময় পরিমাপের) একটা মানদণ্ড হিসেবে ধরা হয়।
প্রযুক্তির চমৎকার
এই সিজিয়াম ফোয়ারা ঘড়িতে এতগুলো প্রযুক্তির সম্মিলন ঘটেছে যে তার পিছনে সেই ১৯৮১ থেকে শুরু করে আটজন নোবেলজয়ী এবং অসংখ্য আরো অনেক গবেষকের পরিশ্রম গেছে। তাদের গবেষণার বিষয়ও ছিল বিবিধরকম: লেজারের আবিষ্কার থেকে শুরু করে লেজার দিয়ে পরমাণুদের ঠাণ্ডা ও বন্দী করা, লেজার অপটিক্স গবেষণা, সূক্ষ্ম স্পেক্ট্রোস্কোপি (precision spectroscopy), অত্যাধুনিক ইলেক্ট্রনিক্স ও নিয়ন্ত্রণ ব্যবস্থা (control system), এবং আরও অনেক কিছু।
যদিও বেশ কিছু দেশ এই ঘড়ির ব্যবহার করতে শুরু করেছে, এদের আরো উন্নত করার কাজ এখনো অব্যাহত। সেখানে নতুন নতুন প্রযুক্তির ব্যবহার হচ্ছে, যেমন আলোক কম্পাঙ্ক চিরুনি (Optical frequency comb), ইত্যাদি। আজকাল সব দেশই আলোক পারমাণবিক ঘড়ি (Optical atomic clock) তৈরির দিকে মনোযোগী হয়েছে কারণ সেটা সিজিয়াম ঘড়ির থেকে আরও নিখুঁত সময় দেয়। সবচেয়ে ভালো আলোক পারমাণবিক ঘড়ির সঠিকতা ৯.৩×১০–১৯, যার মানে ৩,৩৭০ কোটি বছরে তার পরিমাপে ১ সেকেন্ড ভুল হতে পারে। সেখানে সিজিয়াম ফোয়ারা ঘড়ির সঠিকতা ১.৬×১০–১৬। বলাই, বাহুল্য সেই আলোক পারমাণবিক ঘড়ির কর্মপন্থাটাও তস্য জটিল।
এই ধরনের পরীক্ষামূলক গবেষণা চট করে শেষ হবার নয়, আগামী ভবিষ্যতে আরো অনেক কিছু ঘটতে পারে। এই প্রযুক্তির উন্নতি শুধুমাত্র আরও নিখুঁত সময় গণনাতেই যে কাজে লাগে, তা নয়। তাত্ত্বিক পদার্থবিদ্যার নানা মৌলিক প্রশ্নের উত্তর দিতেও এগুলো কাজ লাগতে পারে। প্রশ্নগুলো হতে পারে ব্রহ্মাণ্ডের অতীত জানা কিংবা স্ট্যান্ডার্ড মডেল (Standard Model) পরীক্ষা করার মতো মৌলিক প্রশ্নও। ভারতের বিভিন্ন পরীক্ষাগারের সাথে সাথে আমাদের নিজস্ব গবেষণা কেন্দ্রেও (Precision & Quantum Measurement-lab or PQM-lab at Inter University Centre for Astronomy and Astrophysics in Pune) এই নিয়ে বেশ কিছু কাজ বিপুল উদ্যমে এগিয়ে চলেছে।
উৎসাহী পাঠকদের জন্য
কিভাবে সময় গণনার সঠিকতা বেড়েছে, তার একটা কালানুক্রমিক ইতিহাস দেওয়া হলো।
1945 I. Rabi suggested clock using atomic beam magnetic resonance technique.
1949 Ramsey’s oscillatory field technique.
1955 First cesium atomic clock by L. Essen and J. V. L. Parry (NPL, UK).
1958 Commercialization of cesium beam clock.
1967 First redefinition of second in terms of cesium clock (Primary clock).
1975 Proposals for laser cooling of atoms and ions.
1978 Laser cooling of trapped ions.
1980 GPS satellite navigation introduced.
1993 Cs-fountain clock by A. Clairon et al. (Observatory de Paris, France).
1997 Cesium fountain based SI definition second (Amendment).
1999 First optical-frequency measurement with femtosecond combs.
2001 Concept of single ion optical clock by Jim Bergquist et al. (NIST, USA).
2001 Demonstration of Optical ion clock by S. A. Didamas et al. (NIST, USA)
2002 Concept of an optical lattice clock by H. Katori et al. (Univ. Tokyo, Japan)
2003 Concept of Nuclear optical clock by E. Peik et al. (PTB, Germany)
2005 Demonstration of Optical lattice clock by M. Takamoto et al. (Univ. Tokyo, Japan)
2011 Chip scale microwave atomic clock.
2012 Proposal to use highly charged ions as clocks.
2019 Deep space atomic clock (NASA, USA).
2019 The best optical atomic clock with accuracy 9.4×10-19 (1 s inaccuracy over 33.7 billion years).
2026 Expected Second redefinition of SI second with Optical clock.
সূত্র
[১] S. Weyers et al. Metrologia 55, 789 (2018).
[২] S. De et al., Current Science 106, 1348 (2014).
[৩] https://www.nist.gov/pml/time-and-frequency-division/primary-standard-nist-f1
[৪] M. Kumahai et al., Metrologia 45, 139 (2008).