সনাতন কম্পিউটার বনাম কোয়ান্টাম কম্পিউটার 

রাজীবুল(বিজ্ঞান): কম্পিউটার তো অনেকদিন ধরেই আছে। আমরা ছোটবেলায় হয়তো প্রথম কম্পিউটার দেখেছিলাম ট্রেনের টিকিট কাটতে গিয়ে অথবা লাইব্রেরিতে। তারপর ধীরে ধীরে বাড়িতে কম্পিউটার এল। প্রথমে ডেস্কটপ এল, তারপরে ল্যাপটপ। পকেটের মধ্যে যে স্মার্টফোন রয়েছে সেটাও এক ধরনের কম্পিউটার। আমরা খাবার অর্ডার করি ফোনের অ্যাপের মাধ্যমে সেটাও কম্পিউটারের সুফল। Ola, Uber ইত্যাদি অ্যাপের মাধ্যমে যাতায়াত করা হয় সেটাও এক ধরনের কম্পিউটারের সুফল। এসব ছাড়া আমাদের বর্তমান জীবন ভাবা খুবই মুশকিল। তাই না?

ডাঃ অনির্বাণ চৌধুরী: নিশ্চয়ই। কম্পিউটার ছাড়া তো জীবন ভাবাই যায় না। এই যে বললে খাবার অর্ডার করা, এই ধরনের একটা প্রযুক্তি যে হতে পারে সেটা কি কুড়ি বছর আগে ভাবতেও পারতাম? এই নতুন প্রযুক্তি দিয়ে যে অনেক ধরনের কাজ করা যায় এটা সত্যিই একটা অলৌকিক ঘটনা। 

ঠিক ঠিক, একেবারেই তাই। কিন্তু এখান থেকে একটা প্রশ্ন আসতে পারে। এই যে আমরা চারদিকে এত ধরনের কম্পিউটার ব্যবহার করছি, তারপরেও বিজ্ঞানীরা কোয়ান্টাম কম্পিউটার আবিষ্কারের চেষ্টা করছেন কেন? দরকার কী? এখনই তো এত রকমের কম্পিউটার রয়েছে। 

প্রথম কথা হচ্ছে যে নতুন প্রযুক্তি এলে তার কী প্রয়োগ হতে পারে তা অনেকসময় আমাদের ধারণার বাইরে। কোয়ান্টাম কম্পিউটার একটি সম্পূর্ণ নতুন ধরনের কম্পিউটারের প্রযুক্তি। এটা আমাদের এখনকার কম্পিউটারের ব্যবহারে একটা বিপ্লব আনতে পারে। 

এটাকে সম্পূর্ণ নতুন কম্পিউটার প্রযুক্তি বলছো কেন? সেটা একটু খুলে বলো।

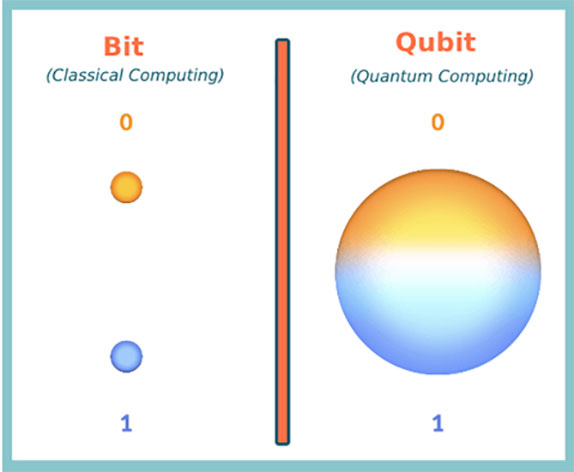
নিশ্চয়ই। এই যে বললে স্মার্টফোন, ডেস্কটপ, ল্যাপটপ, সুপার কম্পিউটার ইত্যাদি – এগুলো কিন্তু আদতে একই প্রযুক্তিতে চলে। এতে কিছু চিপ (Chip) থাকে যা তৈরি হয় ট্রানজিস্টর (Transistor) দিয়ে। সহজ কথায় ট্রানজিস্টর এক ধরনের সুইচ। এটা অন বা অফ হতে পারে। কম্পিউটার সায়েন্সের ভাষায় এটা শূন্য বা এক হতে পারে। কম্পিউটারে যে গণনা হয় সেটা এই শূন্য আর একেরই খেলা। তাকে আমরা বলি বুলিয়ান লজিক (Boolean logic)।

কোয়ান্টাম কম্পিউটার কি একইরকম নয়? এর থেকে আলাদা কিছু জিনিস?

কোয়ান্টাম কম্পিউটার এর থেকে সম্পূর্ণ আলাদা জিনিস। এখানে বুলিয়ান লজিকের জায়গায় চলে কোয়ান্টাম মেকানিক্স। এতে ট্রানজিস্টর থাকে না। তার জায়গায় কাজ করে অণু-পরমাণুরা।

ট্রানজিস্টরের কথা বলে ভালো করলে। আমরা যখন কম্পিউটারে কাজ করি, একটা সফটওয়্যার বা অ্যাপ নিয়ে কাজ করি। তখন আমাদের সাধারণত মনে হয় না যে গণনাগুলো আদতে হচ্ছে সিপিইউ (CPU) এর ভেতর থাকা অসংখ্য ট্রানজিস্টরে। ট্রানজিস্টরের মধ্য দিয়ে কারেন্ট যাচ্ছে, তার ফলে তার অবস্থা পাল্টাচ্ছে। একটা অবস্থাকে আমরা “শূন্য” বলছি, আরেকটাকে “এক”। 

আমরা যদি এই কম্পিউটারটাকে নিয়ে অন্য কোনো জগতে চলে যাই, যেখানে প্রকৃতির নিয়ম আলাদা, কারেন্ট আর ভোল্টেজের মধ্যে সম্পর্ক আলাদা, তাহলে কিন্তু কম্পিউটারের গণনাটাই পাল্টে যাবে।

ঠিক একইভাবে পাল্টাতে পারে যদি আমরা একটা ট্রানজিস্টরের জায়গায় এক একটা পরমাণু দিয়ে একটা কম্পিউটার বানাই। ট্রানজিস্টর যেহেতু নেই, আমরা ট্রানজিস্টরের অবস্থাকে বিট বললাম না। আমরা বিট বললাম পরমাণুর মধ্যে ইলেকট্রন-টা কোন শক্তিস্তরে রয়েছে সেটাকে। এই যুক্তিতে যদি একটা কম্পিউটার বানাই, তাহলে সেই কম্পিউটার আমাদের এখনকার কম্পিউটারের মতো একই ভাবে কাজ করবে না আলাদা হবে? 

এই চিন্তা ভাবনা থেকেই কোয়ান্টাম কম্পিউটারের শুরু। কারণ পরমাণু যে নিয়ম মেনে চলে, তা কোয়ান্টাম ফিজিক্সের নিয়ম। এতে অনেক অদ্ভুত সব জিনিস হয়। এখানে পরমাণু শুধুমাত্র শূন্য আর এক নয়; তার মাঝে আরো অনেক ধরনের স্তরে থাকতে পারে। যাদের সুপারপোজিশন (Superposition) বলে। বা এন্ট্যাঙ্গলমেন্ট (Entanglement) এর মতো অদ্ভুত সব জিনিসও হয়। এই নিয়মগুলো কিন্তু সম্পূর্ণ আলাদা। 

একেবারেই তাই। এই নতুন কম্পিউটার কি আরো নতুন জিনিস করতে পারবে? এটাই ছিল বিজ্ঞানীদের প্রশ্ন। দেখা গেছে যে উত্তরটা হ্যাঁ। আমরা এমন কিছু করতে পারি যেটা এখনকার কম্পিউটারে ভাবাও যায় না।

সুপার কম্পিউটারও যখন পেরে ওঠে না

একটা উদাহরণ দেওয়া যাক। কারণ আমাদের পাঠকদের মধ্যে অনেকেরই মনে হবে, এমন কী সমস্যা আছে যা আমাদের এখনকার চলতি কম্পিউটার সমাধান করতে পারে না কিন্তু কোয়ান্টাম কম্পিউটার পারে?

শুরু করা যাক একটা অংকের সমস্যা দিয়ে। একটা খুবই বিখ্যাত উদাহরণ কোয়ান্টাম কম্পিউটারে। এটা হচ্ছে উৎপাদক বিশ্লেষণ (prime factorization)। 

এটা ছোটবেলায় আমরা করেছি। হাইস্কুলেও করেছি। 

হ্যাঁ, হাইস্কুলে প্রচুর উৎপাদকে বিশ্লেষণ করতে হয়েছে। পনেরোকে উৎপাদকে ভাঙলে তিন আর পাঁচ পাওয়া যেত। একুশে তিন আর সাত। এবার করা যাক 97। 

97 হচ্ছে মৌলিক সংখ্যা, এর কোনো উৎপাদক নেই। 1 আর 97 রয়েছে, তার বাইরে কিছু নেই। 

ঠিক। তাহলে আরেকটু বড় সংখ্যায় করা যাক — 5382।

এটা তুমি মুখে করতে পারবে না। দুই হবে একটা। কিন্তু তার বাইরে কী হবে, সেটা মুখে করা মুশকিল। তবে এটা তো কম্পিউটার করে দেবে। আমি একটা কম্পিউটারের প্রোগ্রাম লিখতে পারি, তাতে কম্পিউটার দেখবে এটাকে দুই দিয়ে ভাগ করা যায় কি না, তিন দিয়ে ভাগ করা যায় কি না, চার দিয়ে ভাগ করা যায় কি না। এইভাবে ভাগ করে করে কম্পিউটার বার করে দিতে পারবে। আমি পারবো না এই মুহূর্তে। 

কম্পিউটার এক সেকেন্ডের কমে করে দেবে। কিন্তু কম্পিউটারে কি নিচে দেওয়া এই বিশাল বড় সংখ্যাটাকে উৎপাদকে বিশ্লেষণ করতে পারে?

এটা কম্পিউটার করতে পারবে কি না সেটা হয়তো বলা মুশকিল। পারবে কি?

বলে দিই। এখন যে সবচেয়ে শক্তিশালী সুপার কম্পিউটার রয়েছে সেটাও এটা করতে পারেনি। 

আচ্ছা মানে লোকজন চেষ্টা করেছে কিন্তু পারেনি।

হ্যাঁ। 

কেন পারেনি?

কারণ উৎপাদকে বিশ্লেষণ করাটা আসলে খুব জটিল একটা সমস্যা। এটা করতে এক্সপোনেনশিয়াল (exponential) সময় লাগে।

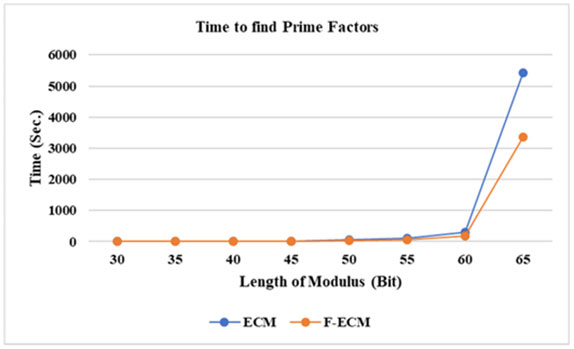
এক্সপোনেনশিয়াল মানে কী জিনিস? 

এক্সপোনেনশিয়াল হচ্ছে এমন একটা জিনিস, যেটা খুব দ্রুত বেড়ে যায়।

মানে সংখ্যাটা যতটা বড় আর কম্পিউটারে যতটা সময় লাগছে, সেটার কথা বলছো?

একদম। এখানে সংখ্যাটা দেখো। পুরো একটা পাতা ভরে রয়েছে। এটাকে উৎপাদকে বিশ্লেষণ করতে যে সময় লাগবে সেই সময়টাকে লিখতে হয়তো আরো 10 পাতা ভরে যাবে।

আচ্ছা। 

এর মানে হল, একটা ছোট সংখ্যাকে বিশ্লেষণ করতে যে সময় লাগবে তার থেকে দ্বিগুণ লম্বা একটা সংখ্যা দিলে দ্বিগুণের অনেক বেশি সময় লাগবে। এটাকেই বলে এক্সপোনেনশিয়াল বৃদ্ধি।

ছোটবেলায় শোনা একটা গল্প মনে পড়ছে। রাজার ফকিরের গল্প। গল্পতে ছিল, রাজা ফকিরকে বলল, তুমি যা চাও তাই পাবে। ফকির রাজাকে বলল, “মহারাজ আমি বেশি কিছু চাই না। আজকে আপনি আমাকে একটা ধান দিন, আগামীকাল দুটো ধান। তারপরের দিন চারটে। তারপরের দিন 8 টা। এই করে বাড়তে থাকবে।” রাজা তখন ভেবেছিলেন: “এ তো মূর্খ। আমি রাজা, আমার কাছ থেকে সোনা দানা হিরে চাওয়ার বদলে সে চাইছে একটু ধান।” 

কিন্তু ফকিরের শর্ত ছিল যে এক মাস ধরে তাকে এইভাবেই বাড়িয়ে বাড়িয়ে ধান দিতে হবে। এতে শেষদিনে এত ধান লাগে যে তার ওজন প্রায় 25 টনেরও বেশি।

যেভাবে ধানের সংখ্যা এক্সপোনেনশিয়াল হারে বেড়েছিল, উৎপাদকে বিশ্লেষণ করতে গেলে সংখ্যা বড় হওয়ার সাথে সাথে একটা কম্পিউটারের গণনার সময়টাও এরকম  এক্সপোনেনশিয়াল হারে বাড়তে থাকে। 

কিন্তু যদি আমরা একটা কোয়ান্টাম কম্পিউটার বানাতে পারি, তাহলে উৎপাদক বিশ্লেষণের সমস্যাটা খুব সহজভাবেই সমাধান হয়ে যাবে। এতটা সময় আর লাগবে না। লাগবে পলিনোমিয়াল টাইম (polynomial time)। অর্থাৎ, সংখ্যাটা যে হারে বাড়বে, বিশ্লেষণ করার সমস্যাটাও সমানুপাতিক হারে বাড়বে।

এটা কি প্রমাণ করা গেছে? 

হ্যাঁ, এটা প্রমাণ করা গেছে। এটা দেখিয়েছিলেন MIT-র কম্পিউটার সাইন্টিস্ট, পিটার শোর (1994 সালে)। 

আচ্ছা। তার মানে কারো যদি কোয়ান্টাম কম্পিউটার থাকে সে এত বড় সংখ্যাটার উৎপাদকে বিশ্লেষণ করে দিতে পারবে? 

হ্যাঁ।

আশীর্বাদ না অভিশাপ? 

আচ্ছা উৎপাদকে বিশ্লেষণ না হয় হল। ভাগ্যিস ছোটবেলায় কোনো মাস্টারমশাই এত বড় সংখ্যা দেননি। কিন্তু এই সমস্যাটা কেন সমাধান করা দরকার? এটা নিয়ে আমরা ভাবছি কেন? এটা কি শুধুমাত্র একটা অংকেরই সমস্যা না দৈনন্দিন জীবনে কোনো প্রয়োগ আছে? 

এই যে এই সমস্যাটা এত যন্ত্রনাদায়ক, এটাই আমাদের রাত্রে নিশ্চিন্তে ঘুমোতে দেয়।

আচ্ছা। 

আমাদের ব্যাংকের যে লেনদেন হয়, ক্রেডিট কার্ড যখন ব্যবহার করছি আর টাকা কাটছে, সেগুলো সুরক্ষিত থাকে বিভিন্ন ধরনের এনক্রিপশন (encryption) দিয়ে। এই এনক্রিপশন পদ্ধতির একটা অংশ করা হচ্ছে উৎপাদকে বিশ্লেষণ করার সমস্যা দিয়ে।

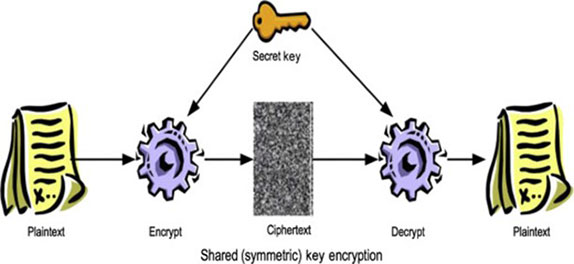
এনক্রিপশন মানে কী? কোনো হ্যাকার (hacker) যদি  আমাদের ক্রেডিট কার্ড ব্যবহার থেকে উৎপন্ন সিগনালটা পেয়ে যায়, তাহলে সে যাতে আমাদের কোনো তথ্যাবলি না পেয়ে যায়, সেইটা নিশ্চিত করার পদ্ধতি? 

হ্যাঁ, হ্যাকারকে যদি সেই তথ্যগুলি পেতে হয়, তাকে একটা খুব কঠিন উৎপাদকে বিশ্লেষণ করতে হবে। এই যে একটা বড় সংখ্যা দিলাম, এটারই উৎপাদকে বিশ্লেষণ করতে হবে। এখনকার কোনো কম্পিউটারই এটা করতে পারবে না। 

কিন্তু কোয়ান্টাম কম্পিউটার হলে পারবে? 

হ্যাঁ।

তাহলে কোয়ান্টাম কম্পিউটার আবিষ্কার করার চেষ্টা হচ্ছে কেন? আমরা ছোটবেলায় তো পড়তাম, বিজ্ঞান আশীর্বাদ না অভিশাপ? এ তো মনে হচ্ছে কোয়ান্টাম কম্পিউটারে এলে আমার রাতের ঘুম চলে যাবে। আমার ব্যাংক অ্যাকাউন্টে মুশকিল হয়ে যাবে। তাহলে তো সমস্যা সেটা। 

ঘুম গায়েব হওয়ার মতো চিন্তা এখন করার দরকার নেই। কারণ এখন যে কোয়ান্টাম কম্পিউটার বানানো চলছে সেগুলোই উৎপাদক বিশ্লেষণ করার ধারে কাছেও আসেনি। এবং আগামী দশকেও যে সেই ধরনের কম্পিউটার তৈরি হবে তার সম্ভাবনাও খুবই কম। 

আচ্ছা এটা এখনো অবধি তাত্ত্বিক জায়গাতেই আছে। আমার মতো এক্সপেরিমেন্টালিস্ট-রা যেটুকু করতে পারছে সেগুলো অনেকটাই ছোট স্তরে। 

একদম একদম। 

আচ্ছা। 

কোয়ান্টাম কম্পিউটারে শুধুমাত্র যে উৎপাদক বিশ্লেষণ হয় শুধু তাই নয়, আরো অনেক ভালো ব্যবহার রয়েছে। এই আলোচনার মধ্যে আমরা সেগুলো নিয়ে কথা বলবো। 

এই যে কোয়ান্টাম কম্পিউটার উৎপাদকে বিশ্লেষণ করে এনক্রিপশন ভাঙতে পারে, সেইটা যাতে ঠেকানো যায়, সে নিয়েও কি গবেষণা হচ্ছে? 

হ্যাঁ, সেটা নিয়েও অনেকে গবেষণা করছে। কোয়ান্টাম হ্যাকারদের থেকে বাঁচানোর জন্য, লোকে অনেক ধরনের নতুন এনক্রিপশন পদ্ধতি ভেবেছেন। এমনকি কোয়ান্টাম মেকানিক্স ব্যবহার করেও সে ধরনের এনক্রিপশন বানানো যায়। 

আচ্ছা। মানে সেই বিজ্ঞানীরা কত ভালো কাজ করবেন তার ওপর নির্ভর করবে আমাদের ভবিষ্যতে একাউন্ট কতটা সুরক্ষিত থাকবে। 

একদম। 

কোয়ান্টাম কম্পিউটিং-এর গোড়ার কথা 

আচ্ছা, কোয়ান্টাম কম্পিউটিং এর ইতিহাসের কথা যদি আমরা ভাবি তাহলে প্রথম নাম মাথায় আসে রিচার্ড ফাইনম্যানের (Richard Feynman)। 1980-র দিকে ইনি প্রথম কোয়ান্টাম কম্পিউটিং-এর ধারণাটি তুলে ধরেন। এই সময় আর কারো নাম পাওয়া যায়?

অনির্বাণ: রিচার্ড ফাইনম্যান তো অনেক বড় পদার্থ বিজ্ঞানী। কিন্তু ইনি ছাড়াও আরো দু-জন বড় বিজ্ঞানী ভাবছিলেন কীভাবে কোয়ান্টাম মেকানিক্স দিয়ে কম্পিউটিং করা যেতে পারে। একজন হলেন আমেরিকান পদার্থবিজ্ঞানী পল বেনিয়ফ (Paul Benioff), অপরজন রাশিয়ান পদার্থবিজ্ঞানী ইউরি ম্যাণীন (Yuri Manin)। 

তাছাড়াও এসময় কোয়ান্টাম ফাউন্ডেশন (quantum foundations) এবং কোয়ান্টাম অপটিক্স (quantum optics) নিয়েও কিছু কাজ চলছিল।

এই কোয়ান্টাম ফাউন্ডেশন যে বললে সেটা একটা গুরুত্বপূর্ণ কথা। কারণ আমরা দেখেছি, যখন কোনো নতুন প্রযুক্তির উদ্ভব হয়, সেটা হঠাৎ করে হয় না। তার পেছনে বহুদিনের কাজকর্ম থেকে থাকে, তারপরে সেটা সম্ভব হয়। 

ফাউন্ডেশন বললে বলে “নো ক্লোনিং থিওরেম”-এর (no-cloning theorem) নামটা প্রথমে মাথায় আসছে। এই বিষয়টা খুব মজার লাগে আমার।

হ্যাঁ, থিওরেম-টার সারমর্ম হলো যে তথ্য নকল করা যাবে না। 

যেমন ধরো আমাদের কাছে একই বইয়ের দুটো অনুলিপি রয়েছে, আমরা আবার আরো জেরক্স করাতে পারি। কম্পিউটারে কপি-পেস্ট করতে পারি। যদি জেরক্স দোকানে নিয়ে যাই, যিনি জেরক্স করছেন, তাকে কিন্তু বইটা পড়তে হবে না, তিনি এমনিই জেরক্স করে দেবেন। কোয়ান্টাম মেকানিক্সে এই কপি-পেস্ট জিনিসটা করা যায় না। তাই না?

কোয়ান্টাম মেকানিক্সে আমরা খুবই সূক্ষ্ম স্তরে কাজ করছি। যেহেতু আমরা একেকটা পরমাণুর ভেতরের তথ্যাবলি নিয়ে কাজ করি, তথ্যগুলো যখনই আমি কপি পেস্ট করতে যাই তখনই সেটা ঘেঁটে যায়। যে কারণে কোয়ান্টাম কম্পিউটার ক্লাসিক্যাল কম্পিউটারের থেকে অনেকটাই আলাদা।

সেই। অনেকের মনে হতে পারে এই যে কপি-পেস্ট করতে পারছে না এটা কোয়ান্টাম কম্পিউটারের দুর্বলতা। কিন্তু সেটা নয়। এই যে এই কপি পেস্ট করা যায় না এটা থেকে বোঝা যায় যে কোয়ান্টাম ইনফরমেশন (quantum information) ব্যাপারটা অন্যরকম। আর এই অন্যরকম জিনিসটা ব্যবহার করেই আমরা নতুন কিছু করতে পারি। 

এই প্রসঙ্গে, কোয়ান্টাম ফাউন্ডেশন-এর আরো একটা উদ্ভাবনা মাথায় আসে, যেটা হলো বেলস ইন-ইকুয়ালিটি (Bell’s inequality)। এটার কথা হয়তো শুনে থাকবে কেউ কেউ।

2022 সালে ফিজিক্সের নোবেল পুরস্কারটি  তিনজন বিজ্ঞানীকে দেওয়া হয় বেলস ইন-ইকুয়ালিটি নিয়ে গবেষণার জন্যই।

একদমই। বেলস ইন-ইকুয়ালিটির তত্ত্ব আবিষ্কার হয়েছিল 1940-এর দশকে। কিন্তু এই তত্ত্বের পরীক্ষামূলক প্রমাণ, যেটা এর সবথেকে গুরুত্বপূর্ণ দিক, সেটা পাওয়া যায় সত্তর আশির দশকে। 

একটু সহজ করে বলো, বেলস ইন-ইকুয়ালিটি ব্যাপারটা কী? 

বেলস ইন-ইকুয়ালিটি বলে যে, দুটি কণা যদি ক্লাসিকাল বা নিউটনিয়ান পদার্থবিজ্ঞান মেনে চলে, তাদের মধ্যে সম্পর্কটা একটা নির্দিষ্ট রকমের হয়ে থাকে। বেলস ইন-ইকুয়ালিটির এই নির্দিষ্ট লিমিটটা কোয়ান্টাম অণু-পরমাণুরা ভাঙতে পারে। এই তত্ত্বের পরীক্ষামূলক প্রমাণই সত্তর আশির দশকে পাওয়া যায়। তার মানে কোয়ান্টাম অণু-পরমাণুতে এমন একটা কিছু ব্যাপার রয়েছে যেটা নিউটনিয়ান ফিজিক্স দিয়ে ব্যাখ্যা করা যায় না। 

আইনস্টাইন নিজে অনেক কাজ করেছেন কোয়ান্টাম মেকানিক্সের শুরুর দিকে। উনি কিন্তু কোনোদিনই কোয়ান্টাম মেকানিক্স নিয়ে স্বচ্ছন্দ ছিলেন না। 

হ্যাঁ, উনি বলেছিলেন এটা ভুতুড়ে কাণ্ডকারখানা, এটাকে উনি মানতে পারছেন না।

এটাকে ‘Spooky action at a distance’ বলা হয়। মানে, দুটো কোয়ান্টাম পার্টিকলকে তুমি যত দূরেই রাখো না কেন, তাদের দু-জনের মধ্যে একটা ভুতুড়ে সম্পর্ক রয়েছে। এটাই আমরা ব্যবহার করছি কোয়ান্টাম কম্পিউটিং-এ। 

আইনস্টাইনের ধারণা ছিল এটা ভুল। কিন্তু সত্তর আশির দশকে যে পরীক্ষাগুলি হয়, তা প্রমাণ করে আইনস্টাইনই এক্ষেত্রে ভুল ছিলেন। 

পদার্থ বিজ্ঞানে যে কেউ ভুল হতে পারে। 

একেবারে। বিজ্ঞানে যে কেউ ভুল হতে পারে। 

এই যে ফাউন্ডেশনের কথা বললাম, তার উপর ভিত্তি করে নব্বইয়ের দশকের শুরুর দিকে পিটার শোর (Peter Shor) কোয়ান্টাম কম্পিউটিং-এর মাধ্যমে উৎপাদকে বিশ্লেষণের পদ্ধতি (prime factorization algorithm) তৈরি করেন। আমি যতটা ইতিহাস সম্পর্কে শুনেছি, এই ঘটনার পর থেকেই কোয়ান্টাম কম্পিউটেশনের জগতে একটা উৎসাহের সৃষ্টি হয়। 

নিশ্চয়ই। তখনই সরকারি দপ্তর, প্রচুর ফান্ডিং এজেন্সি, ন্যাশনাল সিকিউরিটি এজেন্সি, এমনকি মিলিটারিও নড়েচড়ে বসলো। তার কারণ হচ্ছে এনক্রিপশন (encryption) ভাঙার ব্যাপারটা মিলিটারিদের ক্ষেত্রে খুবই গুরুত্বপূর্ণ। যদি কোনো গভর্মেন্ট বা মিলিটারি এমন সংকেত পাঠাতে চায় যেটা শত্রুপক্ষ পড়তে পারবে না, তাহলে সেটাকে এনক্রিপ্ট (encrypt) করে পাঠাতে পারে। কিন্তু শত্রুপক্ষ যদি সেই এনক্রিপশন ভেঙে ফেলে তাহলে তারা চূড়ান্ত সুবিধে পেতে পারে। 

যেমন দ্বিতীয় বিশ্বযুদ্ধের সময় জার্মান এনিগমা মেশিনটার এনক্রিপশন ভেঙেছিল ব্রিটেনের আলান টিউরিং, যাকে সাধারণ কম্পিউটারের অন্যতম পথিকৃৎ বলা হয়। 

হ্যাঁ, বলা যায় সেখান থেকেই কম্পিউটার সাইন্সের শুরু।

তাহলে এই এনক্রিপশন ভাঙতে পারার মোটিভেশনটা কোয়ান্টাম কম্পিউটিং-এর জন্য খুবই গুরুত্বপূর্ণ। 

হ্যাঁ, এরপরে আসে গ্রোভার সার্চ অ্যালগোরিদম (Grover’s algorithm)। যেটা কোয়ান্টাম কম্পিউটিং-এর জন্য একটা গুরুত্বপূর্ণ মাইলফলক। 

মানে, তখন বিভিন্ন বিজ্ঞানীরা কোয়ান্টাম ফাউন্ডেশন ব্যবহার করে নানা ধরনের অ্যালগোরিদম আনতে থাকলেন। 

নিশ্চয়ই। এখন সেই আলগোরিদম গুলোর বিভিন্ন ধরনের ব্যবহার রয়েছে, যেমন মেশিন লার্নিং বা ডাটা সায়েন্সের ক্ষেত্রে। 

তাহলে ফাউন্ডেশন নিয়ে আমরা কথা বললাম। ফাউন্ডেশন-এর উপর তৈরি নানা ধরনের অ্যালগোরিদম ও তা দিয়ে সমস্যা সমাধানের প্রক্রিয়া নিয়েও কথা হল। এছাড়াও কোয়ান্টাম কম্পিউটিং-এর জগতে ওই নব্বইয়ের দশকে অন্য কোনো ধারায় কাজ হচ্ছিল?

এই সময় আরেকটা খুব গুরুত্বপূর্ণ বিষয় নিয়ে কাজ হচ্ছিল, সেটা হচ্ছে কোয়ান্টাম এরর কারেকশন (quantum error correction)। 

কম্পিউটারের ভুল শোধরানো 

এরর মানে তো ভুল!

হ্যাঁ। কম্পিউটেশন মানে গণনা, আর গণনা করতে গিয়ে আমরা তো ভুল করিই, কম্পিউটারও করে। 

কীভাবে?

কম্পিউটারে গণনা হওয়ার সময় আসলে কী হচ্ছে? কিছু ট্রানজিস্টরের মধ্য দিয়ে কারেন্ট যাচ্ছে, তার ফলে ট্রানজিস্টর অন বা অফ হচ্ছে, যাকে আমরা শূন্য বা এক বলছি। এখন ধরো মহাকাশের মধ্য দিয়ে কোনো একটা কসমিক রশ্মি (cosmic ray) এসে ট্রানজিস্টরের মধ্যে দিয়ে চলে গেল। 

ট্রানজিস্টর তারপরে ঠিকই থাকবে কিন্তু মুহূর্তের জন্য ভোল্টেজটা হয়তো চেঞ্জ হয়ে যাবে। ফলত শূন্যটা এক হয়ে যেতে পারে। ফলে ট্রানজিস্টরে যদি আমরা এক যোগ এক দুই করতে চাই, সেটা শূন্যও হয়ে যেতে পারে। এখানেই ভুল হয়ে গেল। 

এই ভুলটা কিন্তু কোডের ভুল বা সফটওয়্যারের ভুল নয়। ভুল হচ্ছে কারণ একটা কসমিক রশ্মি ট্রানজিস্টরের মধ্যে গিয়ে ভোল্টেজটা বিগড়ে দিয়েছে। 

একেবারে ঠিক। পদার্থভিত্তিক কারণ (physical process) থেকে ভুলটা তৈরি হচ্ছে।

আর এই যে ভুলের কথা বলছো, এইরকম নিশ্চয় হয় না যে কসমিক রশ্মি প্রচুর পরিমাণে ট্রানজিস্টরের অবস্থা বিগড়ে দিচ্ছে।

হ্যাঁ, সেজন্যই আমরা ল্যাপটপ বা কম্পিউটারে সেরকম ভুল দেখতে পারি না। খুবই কম হয়।

কিন্তু কোয়ান্টাম কম্পিউটারে এরকম ভুল হতেই থাকে। এটার জন্য কসমিক রশ্মির অপেক্ষা করতে হবে না। একটা সাধারণ আলোর কণা গিয়েও একটা পরমাণুকে ধাক্কা মেরে দিতে পারে। অথবা পাশ দিয়ে কোনো একটা ট্রাক গেলে তার চুম্বকক্ষেত্রটাও পরমাণুটাকে প্রভাবিত করতে পারে। মানে কোয়ান্টাম কম্পিউটার এরকম ভুল আকচার করতেই থাকে। 

হ্যাঁ। 

তুমি এরর কারেকশনের কথা বলছো। সেই গল্পটা একটু বলো। 

ক্লাসিকাল কম্পিউটারে ভুলটা খুব কমই হয়। আর এতে ভুলটা ঠিক করাও খুবই সোজা। ধরো আমি কোনো একটা গণনা করছি এবং কোনো কারণে সেটা একটু ভুল হয়ে গেল। আমি যেহেতু এই ধরনের ক্লাসিকাল কম্পিউটারে কপি করতে পারি, আমি এই গণনাটাই তিনটে ট্রানজিস্টরে একসাথে (in parallel) করলাম। তারপর আমি তিনটেই তুলনা করে দেখলাম। যে গণনার ফলটা বেশি এসেছে সেটাকেই আমি ঠিক বলে নিলাম। তাই আমরা সহজেই কপি করার মাধ্যমে ঠিক উত্তরটা বুঝতে পারি। 

আচ্ছা। আর আমরা একটু আগেই যে নো-ক্লোনিং বিষয়টা নিয়ে আলোচনা করলাম, তার কারণে কোয়ান্টাম কম্পিউটারে কপি করা যায় না। তাই কোয়ান্টাম কম্পিউটারে এইভাবে নিশ্চয়ই ভুলও ঠিক করা যাবে না। 

একদম। তাই কোয়ান্টাম কম্পিউটারের ভুল ঠিক করার ব্যাপারটা একটু জটিল। 

কিন্তু অসম্ভব নয়। 

একেবারেই অসম্ভব নয়। এটাই ওই সময় কম্পিউটার সাইন্টিস্ট এবং পদার্থবিজ্ঞানীরা তাত্ত্বিকভাবে দেখিয়েছেন। কোয়ান্টাম কম্পিউটারে ভুলটাকে শূন্য করতে হবে না। আমরা যদি কোনো একটা প্রসেস ডিজাইন করতে পারি যাতে এই ভুলটা সবসময় কম থাকে, তাহলেই চলবে। এটাকেই বলে কোয়ান্টাম এরর কারেকশন (quantum error correction), আর কোয়ান্টাম ফল্ট টলারেন্স (quantum fault tolerance)। 

আচ্ছা, এই থিওরিটা আছে বলেই আমাদের মতো এক্সপেরিমেন্টালিস্টরা একটু আশাবাদী যে আমরা প্রচুর খাটাখাটনি করে যদি এই ভুলগুলোকে কম করি, তাহলে একটা সময় বড় স্কেলে কোয়ান্টাম কম্পিউটার বানানো গেলেও যেতে পারে। 

হ্যাঁ, সেজন্যই কোয়ান্টাম কম্পিউটিং -এর বিকাশে এরর কারেকশনটা খুবই গুরুত্বপূর্ণ বিষয়।

প্রচ্ছদের ছবি: https://media.wired.co.uk/photos/60c78558edeb9d79d47f89f2/16:9/w_1920,c_limit/WIRED-Consulting-0506FTQuantum01-1.jpg