সার্চ ইঞ্জিন
ইন্টারনেট এখন আমাদের দেশে (ভারতে) যথেষ্ট সহজলভ্য বলে মনে করা যেতে পারে।
2021 সালের হিসেব মতো এদেশে মোটামুটি 64 কোটির বেশি মানুষ ইন্টারনেট ব্যবহার করতেন [1] — সেবছর দেশের 140 কোটির জনসংখ্যার প্রায় অর্ধেকের কাছাকাছি বলা যেতে পারে। আর 2022 সালে স্মার্টফোন ব্যবহারকারীর সংখ্যা ছিল 66 কোটির কাছাকাছি [2]। এই দুটো ব্যাপারেই পৃথিবীতে আমাদের অবস্থান ছিল দুই নম্বরে – চীনের পরে আর আমেরিকার আগে। বর্তমানে সংখ্যাটা আরো বেশি হবে। স্মার্টফোন তো আমাদের অনেকেরই শরীরের অপরিহার্য অঙ্গ হয়ে উঠেছে।
ইন্টারনেটে আমাদের বিভিন্ন কর্মকাণ্ডের মধ্যে একটা প্রধান কাজ হলো বিভিন্ন ওয়েবসাইট থেকে দরকারি তথ্য সংগ্রহ করা। ইউটিউবের ভিডিও, ফেসবুকের ফ্রেন্ড, ইন্সটাগ্রামের ছবি, আরো অনেককিছু – এই তালিকার শেষ হবে না চট করে।
যার যেটা প্রয়োজন, সেই গুরুত্বপুর্ন ওয়েবপেজগুলি খুঁজে দেওয়ার কাজটা করে ওয়েব সার্চ ইঞ্জিন। যেমন, গুগল, ইয়াহু, বিং, ইত্যাদি।
গুগল সার্চ বনাম বাকিরা
1990 সাল নাগাদ প্রথম সার্চ ইঞ্জিনের ব্যবহার শুরু হয়।
শুরুর দিকের সার্চ ইঞ্জিনের মধ্যে কয়েকটি হল W3Catalog, ALIWEB, JumpStation, WWW Worm, WebCrawler, Go.com, Lycos, Infoseek ইত্যাদি। এদের মধ্যে WebCrawler আর Lycos ছাড়া অন্য কোনোটাই বর্তমানে ব্যবহারযোগ্য নয়। 1995 সালে Yahoo! Search-এর উদ্ভব ঘটে এবং সেটা এখনো চালু রয়েছে।
আজকের বহুপ্রচলিত সার্চ ইঞ্জিন গুগল তার যাত্রা শুরু করে 1998 সালে আমেরিকার স্ট্যানফোর্ড ইউনিভারসিটির দুই ছাত্র, ল্যারি পেজ (Larry Page) আর সারগে ব্রিন (Sergey Brin), এদের হাত ধরে। 1996 সালে তাঁরা ওয়েব সার্চ করার নতুন একটি পদ্ধতি – পেজর্যাঙ্ক (PageRank) উদ্ভাবন করেন। তখন তাঁদের দুজনেরই বয়স মাত্র 23 বছর।
2024 সালের অক্টোবর মাসের হিসেব অনুযায়ী গুগল সার্চ ইঞ্জিন দিয়ে দিনে 27 কোটির বেশি বার ওয়েব সার্চ করা হয়েছে। এটা সারা পৃথিবীর মোট ওয়েব সার্চের 91 শতাংশেরও বেশি। অথচ গুগল যখন যাত্রা শুরু করে, 1998 সালের সেপ্টেম্বর মাসে, তখন দৈনিক সার্চের সংখ্যা ছিল 10 হাজারের কাছাকাছি। এক বছর বাদে সংখ্যাটা বেড়ে দাড়ায় 35 লক্ষর মতো [4]।
টাকাপয়সার হিসেবটা একটু দেখা যাক। 2024 সালে ল্যারি পেজের সম্পত্তির আনুমানিক পরিমাণ 15600 কোটি মার্কিন ডলারের কাছাকাছি। ব্রিনের একটু কম 14600 কোটি মার্কিন ডলার। প্রথমজন পৃথিবীর পঞ্চম আর পরের জন সপ্তম ধনী ব্যক্তি। এখানে অবশ্য একটা কথা বলে রাখা ভালো। গুগল যে শুধুই সাফল্যের মুখই দেখেছে এমন না, তাদের সোশ্যাল মিডিয়া Google+ 2011 সালে যাত্রা শুরু করে 2019 সালে বন্ধ হয়ে যায় [5]।
গুগল কতটা ভালোভাবে কাজ করে একটু বোঝা যাক। আজ অমি গুগলে Football লিখে সার্চ করলাম। 0.29 সেকেন্ডে গুগল প্রায় 322 কোটি Football সম্পর্কিত ওয়েবপেজ দেখাল। এতোগুলি পেজের মধ্যে আমরা সাধারণত প্রথমে দিকের 10-12টি পেজ দেখি আর বাকিগুলো দেখিনা।
গুগল পেজগুলিকে গুরুত্ব অনুসারে সুন্দরভাবে সাজিয়ে দেয়। যেমন প্রথমে Football সম্পর্কে Wikipedia, তারপর Espn India-র Website, এরপর আরো অন্যান্য (তবে এই সার্চ রেজাল্ট বিভিন্ন সময় ও বিভিন্ন ব্যক্তির জন্য বিভিন্ন হতে পারে)। প্রত্যেক সার্চ ইঞ্জিন নিজের মত করে ওয়েবপেজগুলো সাজায়। গুগলের জনপ্রিয়তার একটা কারণ হচ্ছে যে গুগল সবথেকে দরকারি ওয়েবপেজকে ভালোভাবে বাছাই করে আমাদের দেখায়।
ওয়েবপেজ-এর মধ্যে সম্পর্কের গ্রাফ
গুগলের প্রথম সার্চ algorithm ছিল PageRank। সেটা বিভিন্ন ওয়েবপেজের মধ্যে সম্পর্কের ভিত্তিতে কোনো একটা ওয়েবপেজের গুরুত্ব নির্ণয় করতো। যে ওয়েবপেজের বেশি গুরুত্ব, সেটাই সার্চ রেজাল্টে প্রথমের দিকে আসে, বাকিরা যায় পিছিয়ে।
কিন্তু আলাদা আলাদা ওয়েবপেজের মধ্যে সম্পর্কটা কিভাবে বোঝা যায়?
উপরে লেখার মধ্যে যখন ল্যারি পেজের নাম লেখা হলো, সেটা আন্ডারলাইন করা একটা উল্লেখ ছিল। ওর উপর ক্লিক করলে আমরা তাঁর উইকিপিডিয়া পেজ দেখতে পাবো। এই কথাগুলিকে বলা হয় হাইপারলিঙ্ক (hyperlink) – যারা পাঠককে একটি ওয়েবপেজ থেকে সম্পর্কিত অন্য ওয়েবপেজে নিয়ে যায়।
একটা কাগজের উপর একগুচ্ছ ওয়েবপেজকে কিছু বিন্দু দিয়ে চিহ্নিত করা যাক। ধরা যাক, ওয়েবপেজ A এর মধ্যে একটা হাইপারলিঙ্ক আছে যা পাঠককে A থেকে আরেকটা ওয়েবপেজ B-তে নিয়ে যায়। আমরা A থেকে B পর্যন্ত একটি তীর চিহ্ন আঁকব। গণিতের পরিভাষায় এই বিন্দুগুলিকে বলা হয় ভার্টেক্স (vertex), আর তীরগুলিকে বলা হয় লিঙ্ক (link), আর এই ছবিটিকে বলা হয় গ্রাফ (graph)।
হাইপারলিঙ্ক গ্রাফের উদাহরণ
ধরা যাক অমল আর তার চার জন বন্ধু – দেবু, মান্তু, দুর্গা, আর রেবেকা – প্রত্যেকের একটি করে ওয়েব পেজ আছে। একটি কাগজের ওপর আমরা পাঁচটি ওয়েব পেজের জন্য একটি করে ভার্টেক্স আঁকব (নিচের ছবিতে নীল বিন্দু)।
ধরা যাক, অমলের ওয়েব পেজ থেকে তার চার বন্ধুর ওয়েবপেজে হাইপারলিঙ্ক দিয়ে যাওয়া যায়। তাই অমলের থেকে শুরু করে এদের সকলের মধ্যে একটা করে লিঙ্ক থাকবে। এটাও ধরা যাক, অন্য সকলের ওয়েব পেজ থেকে অমলের ওয়েব পেজে হাইপারলিঙ্ক দিয়ে আসা যায়। তাই ওদের সবার থেকে অমলের লিঙ্ক থাকবে।
এখন ধরা যাক, দুর্গার পেজ থেকে রেবেকার পেজে যাওয়া যায় না বা রেবেকার পেজ থেকে দুর্গার পেজে যাওয়া যায় না। তাই রেবেকা এবং দুর্গার মধ্যে কোন লিঙ্ক থাকবে না। মান্তুর পেজ থেকে রেবেকার পেজে যাওয়া যায়, কিন্তু রেবেকার পেজ থেকে মান্তুর পেজে যাওয়া যায় না। তাই মান্তু থেকে রেবেকা পর্যন্ত একটা লিঙ্ক থাকবে কিন্তু রেবেকা থেকে মান্তু পর্যন্ত কোন লিঙ্ক থাকবে না। ওয়েব পেজগুলির এই সম্পর্ককে আমরা নিচের গ্রাফ দিয়ে প্রকাশ করতে পারি।
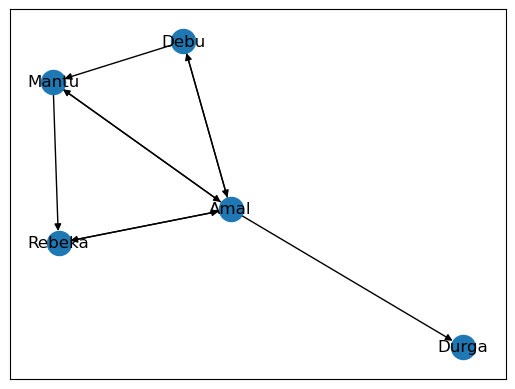
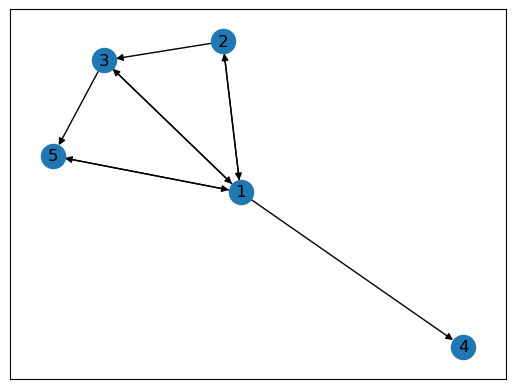
গ্রাফের ভার্টেক্সগুলি যে শুধু নাম দিয়েই চিহ্নিত করা হয় এমন না – হিসেবের সুবিধার জন্য সংখ্যা দিয়েও তাদের সূচিত করা যায়। যেমন – অমলের জন্য 1, দেবুর জন্য 2, ইত্যাদি। গ্রাফের ভার্টেক্স বা লিঙ্কের সংখ্যা প্রয়োজনমতো পরিবর্তন করা যায়।
পেজর্যাঙ্ক কিন্তু যে কোনো ধরনের গ্রাফের জন্য ব্যবহার করা যায়। অর্থাৎ, এটা যে শুধু ওয়েবপেজগুলিকে গুরুত্ব অনুসারে সাজানো পারে এমন না। যেকোনো গ্রাফের ভার্টেক্সগুলির গুরুত্ব আমরা পেজর্যাঙ্ক এর সাহায্যে কষে নিতে পারি। আমাদের সামাজিক সম্পর্কগুলির মধ্যে কে কতটা গুরুত্বপূর্ণ, সেটাও গাণিতিকভাবে হিসেব করা যায়।
ওয়েবপেজে ভিজিট করা আসলে গ্রাফের পথ অনুসরণ
ধরা যাক এই লেখাটি থেকে তুমি ল্যারি পেজ (Larry Page) এর উইকিপিডিয়া পেজে গেলে হাইপারলিঙ্ক অনুসরণ করে। তারপর সেখান থেকে হাইপারলিঙ্ক অনুসরণ করে গেলে মিশিগান ইউনিভারসিটির পাতায়। সেখান থেকে আবার লিঙ্ক অনুসরণ করে পছন্দমতো অন্য যেকোনো একটি পেজে চলে যেতে পারো।
এভাবে পেজ ভিজিট করার সময় তুমি কোনো নিয়মমাফিক চলছো না। অর্থাৎ, একটি পেজে আসবার পরে সেখান থেকে আবার কোন পেজে যাবে, সেটা পূর্বনির্দিষ্ট নয় (random)। ব্যাপারটা অনেকটা লুডোর ছক্কা ফেলার মতো। আমরা জানি 1 থেকে 6-এর মধ্যে কোন একটা সংখ্যা পাবো, কিন্তু কোনটা পাবো তা আগে থেকে বলা যাবে না। মিশিগান ইউনিভার্সিটির পেজটির সঙ্গে যে পেজগুলি লিঙ্ক করা আছে, তুমি নিশ্চিত তার মধ্যে একটিতে যাবে, কিন্তু না যাবার আগে কেউ বলতে পারবে না যে কোনটিতে গিয়েছ।
আর একটা ব্যাপার এখানে বোঝার আছে। যখন তুমি একটি পেজ থেকে আর একটি পেজে যাচ্ছ, তখন আসলে ইন্টারনেট গ্রাফের এক ভার্টেক্স থেকে আর এক ভার্টেক্সে যাচ্ছ গ্রাফের লিঙ্কগুলির দিশা মেনে।
এইটুকু জেনে এবার দেখা যাক, কীভাবে গুগলের পেজর্যাঙ্ক algorithm এই গ্রাফের ভিত্তিতে সার্চ রেজাল্ট-গুলোকে সাজায়।
গ্রাফ থেকে গুগল পেজর্যাঙ্ক (নিজে করো)
অনেকগুলো ওয়েবপেজ একে অপরের সাথে লিঙ্ক করা থাকলে, পেজর্যাঙ্ক নিচের কয়েকটা ধাপ মেনে তাদের গুরুত্ব নির্ণয় করে। এই পদ্ধতিটা তৈরী হয়েছে ল্যারি পেজের পিএইচডি গবেষণা থেকে।
ল্যারি পেজের পিএচডি গবেষণার মূল উদ্দেশ্য ছিল বিভিন্ন বৈজ্ঞানিক গবেষণাপত্রের গুরুত্ব সংখ্যা দিয়ে প্রকাশ করা। পেজর্যাঙ্ক পদ্ধতিটা সেই গবেষণা থেকেই বেরিয়ে এসেছে। পেজ আর ব্রিনের গবেষণাপত্রটি বর্তমান বিশ্বের সর্বাধিক পঠিত গবেষণাপত্রগুলির মধ্যে একটি [8]।
যাইহোক, আপাতত কিকরে পেজর্যাঙ্ক হিসেব করতে হবে সেটা শিখে নেওয়া যাক। পেজর্যাঙ্ক হিসেব করতে নিচের ধাপগুলো অনুসরণ করতে হবে।
ধাপ 1- আমরা যেকোনো গ্রাফকে একটি ম্যাট্রিক্স হিসাবে প্রকাশ করতে পারি। মনে করো একটা গ্রাফ-এ n সংখ্যক ভারটেক্স আছে। আমাদের উদাহরণের জন্য n = 5। এখন একটি n × n স্কোয়ার ম্যাট্রিক্স (square matrix) বানাতে পারি যার (i, j) অবস্থানে 1 লেখা হবে, যদি i থেকে j পর্যন্ত একটা লিঙ্ক থাকে। আর লিঙ্ক না থাকলে আমরা 0 লিখব। এই ম্যাট্রিক্স-কে আমরা বলি অ্যাডজাসেন্সি ম্যাট্রিক্স (adjacency matrix)। আমাদের উপরের গ্রাফের জন্য অ্যাডজাসেন্সি ম্যাট্রিক্স হবে –

ধাপ 2 – এবার অ্যাডজাসেন্সি ম্যাট্রিক্সের প্রত্যেক সারিকে যোগ করে নেবো আর সারিটিকে তার যোগফল দিয়ে ভাগ করে নেবো (এই ধাপের ঠিকঠাক ব্যখ্যা দিতে গ্রাফের উপর random walk-এর ধারনা থাকা দরকার – উৎসাহী পাঠক সেই নিয়ে পড়তে পারেন)। আমাদের উদাহরণের জন্য আমরা নিচের ম্যাট্রিক্সটা পাবো –
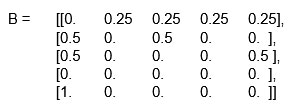
ধাপ 3 – এখন যে ম্যট্রিক্সটা পেলাম তার মধ্যে একটা সারি আছে যার সবগুলি এলিমেন্ট (element) 0 । লক্ষ্য করো এই সারিটি দুর্গার ওয়েব পেজের জন্য। পাঠক যদি দুর্গার ওয়েব পেজে পৌঁছে যায়, তবে হাইপারলিঙ্ক দিয়ে আর কোন পেজে যেতে পারবে না। পাঠককে অন্য যে কোন পেজ থেকে নতুন করে যাত্রা শুরু করতে হবে। পেজর্যাঙ্ক হিসেব করতে এই ধরনের সব ভার্টেক্সের সঙ্গে সম্পর্কিত সারিগুলির সবগুলো এলিমেন্টকে 1/n করে দেব। চার নম্বর সারির প্রত্যেক এলিমেন্টকে আমরা 1/n = 0.2 করে দেবো। এখন নতুন যে B ম্যাট্রিক্সটা পেলাম সেটা হল –
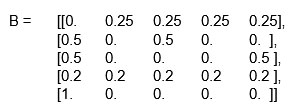
যদি এমন কোন সারি না থাকে যার সব এলিমেন্ট 0, তখন এই ধাপটি না করে আমরা পরের ধাপে চলে যাবো।
ধাপ 4 – সাধারণত ধরে নেওয়া হয় একজন পাঠক একটা পেজ থেকে 85 শতাংশ ক্ষেত্রে হাইপারলিঙ্ক অনুসরণ করে নতুন ওয়েব পেজে যায় আর 15 শতাংশ ক্ষেত্রে নতুন পেজ দেখবার জন্য হাইপারলিঙ্ক অনুসরণ করে না, নতুন করে অন্য কোনো পেজ খোলে। পেজর্যাঙ্ক হিসেব করতে এই ঘটনাটিকেও যুক্ত করা হয়।
এবার একটা ম্যাট্রিক্স J নেওয়া যাক যার সব এলিমেন্ট 1/n । এখন B আর J ম্যাট্রিক্স থেকে Google ম্যাট্রিক্স তৈরি করা যাক –
Google = 0.85 * B + 0.15 * J
আমাদের উদাহরণের জন্য
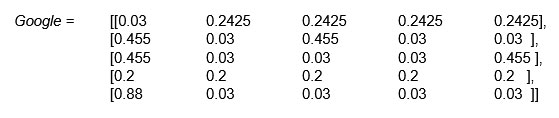
ধাপ 5 – এবার n টি এলিমেন্টের একটি সারি নেওয়া যাক –
R1 = [1 0 0 0 0]
এই R1 সারিটিকে Google ম্যাট্রিক্সের বাম দিকে নিচের মত করে বারবার গুণ করতে হবে।
R2 = R1 * Google
R3 = R2 * Google
R4 = R3 * Google …
এই R1, R2, ইত্যাদি ভার্টেক্সগুলির গুরুত্বের আনুপাতিক মান নির্ধারণ করে। যখন দেখা যাবে নতুন সারিগুলি আর বিশেষ কোন পরিবর্তন হচ্ছে না তখন আমাদের এই গুণ প্রক্রিয়া থামাতে হবে। আমাদের উদাহরণের জন্য সাতবার গুণের পরে পাবো –
R8 = [[0.35 0.12 0.18 0.12 0.21]]
গ্রাফ বড়ো হলে আরও বেশিবার গুণ করতে হতে হবে। Google ম্যাট্রিক্স এমনভাবেই বানানো হয়েছে যে এভাবে গুণ করতে থাকলে গ্রাফের উপর নির্ভর করে একটি নিদিষ্ট সারি পাওয়া যাবে।
ধাপ 6 – এখন R8 সারির ভিত্তিতে আমরা ভার্টেক্সগুলিকে সাজিয়ে নিতে পারি। আমাদের উদাহরণের জন্য পাবো
| ভার্টেক্স এর নাম্বার | নাম | গুরুত্বের মান | পেজর্যাঙ্ক |
| 1 | অমল | 0.35 | 1 |
| 5 | রেবেকা | 0.21 | 2 |
| 3 | মান্তু | 0.18 | 3 |
| 2 | দেবু | 0.12 | 4 |
| 4 | দুর্গা | 0.12 | 5 |
দেবু আর দুর্গার গুরুত্বের মান সমান। এদের যেকোনো একজনকে আগে বা পরে র্যাঙ্ক দেওয়া যায়।
গুগল পেজর্যাঙ্ক-এর পিছনে যে অঙ্ক রয়েছে
3 নাম্বার ধাপে 0 গুলিকে কেন 1/n নেওয়া হল, 4 নাম্বার ধাপে কেন J ম্যাট্রিক্স নেওয়া, আর 5 নাম্বার ধাপে কেন একটি বিশেষ সারি নেওয়া হল – এগুলি বোঝবার জন্য একটু সম্ভাবনা তত্ত্ব (probability theory) জানা দরকার।
ধরা যাক, পাঠক 1 নম্বর পেজ থেকে যাত্রা শুরু করলো। সুতরাং, প্রথম পর্যায়ে 1 নম্বর ভার্টেক্সে পাঠককে পাবার প্রবাবিলিটি 1 আর অন্যান্য ভার্টেক্সে 0। সুতরাং 5 নম্বর ধাপে একটি বিশেষ সারি থেকে শুরু করা হয়েছে:
R1 = [1 0 0 0 0]
R1, R2, ইত্যাদি সারিগুলি হল বিভিন্ন পর্যায়ে পাঠককে একটি পেজে পাবার সম্ভাবনার বিন্যাস (probability distribution)। Google ম্যাট্রিক্স দিয়ে কেন এরকম একটি বিন্যাসকে গুণ করলে আর একটি বিন্যাস পাবো, বা বারবার Google ম্যাট্রিক্স দিয়ে গুণ করতে থাকলে কেন আমরা শেষে একটি নিদৃষ্ট বিন্যাস বা পেজ র্যাঙ্ক ভেক্টর (Page Rank vector) পাবো – সেই গাণিতিক প্রসঙ্গের মধ্যে এই প্রবন্ধে যাচ্ছি না [6]। সাধারণ পাঠকের জন্য বলি, প্রত্যেক ম্যাট্রিক্স-এর কিছু বিশেষত্ব থাকে। Google ম্যাট্রিক্স এমনভাবেই বানানো হয়েছিল যার জন্য এমন হয়।
লক্ষ্য করা যেতে পারে যে দুর্গার ওয়েব পেজে পৌঁছাবার পরে পাঠক হাইপারলিঙ্ক অনুসরণ করে অন্য কোন পেজে যেতে পারবে না। তাই, ধরে নেওয়া যায়, তখন সে n সংখ্যক পেজের মধ্যে থেকে যেকোনো একটিকে 1/n সম্ভাবনা-সহ নির্বাচন করে সেখানে যাবে। n সংখ্যক পেজের মধ্যে থেকে যেকোনো একটিকে নির্বাচন করার সম্ভাবনা হল 1/n। তাই 3 নম্বর ধাপে, চার নম্বর সারির প্রত্যেক এলিমেন্টকে আমরা 1/n = 0.2 করে দিয়েছি।
ঠিক একই কারণে যখন পাঠক হাইপারলিঙ্ক ব্যবহার করে অন্য পেজে করতে চাইছে না, সে যেকোনো পেজে চলে যাবে হাইপারলিঙ্ক ব্যবহার না করে। এই ঘটনাটির ফলাফল অন্তর্ভুক্তির জন্য 4 নাম্বার ধাপে J ম্যাট্রিক্সকে একটি সম্ভাবনা দিয়ে গুণ করে তবে যুক্ত করা হয়েছে।
উপসংহার
গুগল বর্তমানে আর পেজর্যাঙ্ক ব্যবহার করে না। ওয়েব সার্চের জন্য গুগল উদ্ভাবিত আরো কয়েকটা পদ্ধতি বেশ বিখ্যাত – যেগুলো কোন না কোন সময় ব্যবহার হয়েছিল – যেমন গুগল পাণ্ডা, পেঙ্গুইন, হামিংবার্ড, মোবাইল, র্যাঙ্কব্রেন, মেডিক, বারট, এগুলো। উল্লেখ্য – বর্তমানে গুগল তাদের ইন্টারনেট সার্চ করবার পদ্ধতিগুলো বছরে কয়েক হাজার বার আপডেট করে।
কৃতজ্ঞতা স্বীকার
This article is written for the partial fulfillment of the Scientific Social Responsibility of the author’s project “Transmission of quantum information using perfect state transfer” (CRG/2021/001834) funded by the Anusandhan National Research Foundation (ANRF), Government of India. The author acknowledges the financial support from ANRF.
তথ্যসূত্র
[1] https://en.wikipedia.org/wiki/List_of_countries_by_number_of_Internet_users
[2] https://en.wikipedia.org/wiki/List_of_countries_by_smartphone_penetration
[3] https://en.wikipedia.org/wiki/Search_engine
[4] https://explodingtopics.com/blog/google-searches-per-day
[5] https://en.wikipedia.org/wiki/History_of_Google
[6] Google’s PageRank and Beyond: The Science of Search Engine Rankings. Amy N. Langville and Carl D. Meyer. PRINCETON UNIVERSITY PRESS.
[7] https://searchengineland.com/8-major-google-algorithm-updates-explained-282627
[8] Brin, S.; Page, L. (1998). “The anatomy of a large-scale hypertextual Web search engine”. Computer Networks and ISDN Systems. 30 (1–7): 107–117

