একটা টর্নেডো হবে কি হবে না, সেটা কি একটা প্রজাপতির ডানা ঝাপটানোর উপর নির্ভর করতে পারে? ষাটের দশকের শুরুতে গণিতজ্ঞ এবং আবহাওয়াবিদ এডওয়ার্ড লোরেঞ্জ যা দেখলেন, তার মানে কিন্তু সেটাই দাঁড়াচ্ছে। আবহাওয়ার ভবিষ্যদ্বাণী করতে গিয়ে কিছু সমীকরণ লিখেছিলেন তিনি। কম্পিউটারে তার সমাধান করছিলেন। একবার কম্পিউটার চালু করে কফি খেতে গেছিলেন; ফিরে এসে দেখলেন, কম্পিউটার আগামী দু মাসের আবহাওয়া বলে দিয়েছে। কিন্তু আগে একই সমীকরণ সমাধান করে যা বলছিল, তার সাথে এই নতুন সমাধানের কোনো মিল নেই।

প্রথমে উনি ভাবলেন, কম্পিউটার বেগড়বাই করছে। দুটো সমাধানে এত তফাৎ কেন? তারপর সংখ্যাগুলো দেখলেন। উনি লক্ষ্য করলেন যে দুটো সমাধানে শুরুর যে সংখ্যাগুলো উনি দিয়েছিলেন, তাতে একটার থেকে আরেকটার সামান্য তফাৎ ছিল। যাকে বলে round off error, দশমিকের বেশ কিছুটা পরের সংখ্যাগুলো ঝেড়ে ফেললে যা হয়। তফাৎটা এতই কম যে তাকে প্রজাপতির ডানা ঝাপটানো বলা চলে। কিন্তু এই তফাতের ফলে সমাধানে শুরুর দিকের সংখ্যাগুলো কাছাকাছি থাকলেও খুব অল্প সময় পরই তারা দুটো ভিন্ন পথে চলে গেছে। শেষে দু মাস পরের আবহাওয়া দেখলে আর দুটো সমাধানের শুরুর সাদৃশ্যের কিছুই বাকি থাকে না।

সামান্য পরিবর্তনের উপর ভবিষ্যদ্বাণী যদি এতটা নির্ভরশীল হয়ে, তাহলে তো এক্কেবারে চূড়ান্ত ক্যাওস হয়ে যায়! আর কোথায় কোথায় এরকম ক্যাওস হতে পারে? সেই খোঁজ শুরু হলো। 

গণিতজ্ঞ লোরেঞ্জ-এর ওই পর্যবেক্ষণ থেকেই “ক্যাওস” (chaos) নিয়ে গবেষণার শুরু। এর আগেও এই ধারণাটা এসেছে, কিন্তু আবহাওয়ার পূর্বাভাসের ক্ষেত্রে সরাসরি প্রয়োগ আছে বলেই বোধহয় এইবার জোরকদমে গবেষণা শুরু হলো। ক্যাওস-এর উদাহরণ পাওয়া গেল খুব সহজ সিস্টেম-এ। এমন সিস্টেম যেগুলো পাতি নিউটনের সূত্র মেনে চলে।

এমনই একটা সিস্টেম আছে নিচের ছবিটাতে। দুটো আয়তাকার (rectangular) পাত আছে। উপরেরটা একদিকে আটকানো, সেদিকটা নড়ন চড়নের উপায় নেই। নিচেরটা, মানে নীলটার, একটা দিক উপরের পাতটার সাথে আটকানো। দুটো পাতের মধ্যে আটকানো অংশটাতে ঘর্ষণ প্রায় নেই বললেই চলে (frictionless)। নিচের পাতটা যদি ছবিতে যেভাবে দেখানো আছে সেভাবে একদিকে টেনে ছেড়ে দেওয়া হয়, পাত দুটো কীভাবে চলবে?

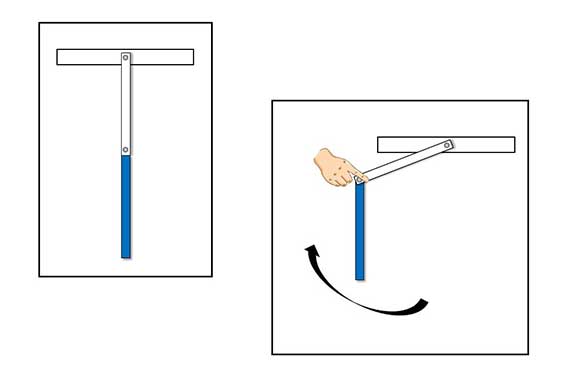
যদি অঙ্ক কষতে বসো, একটু সাবধান করে দিচ্ছি। অঙ্কের সাথে বাস্তবের কিন্তু বিস্তর ফারাক হতে পারে।

অঙ্কের সাথে বাস্তবের মিল 

ইস্কুলে যে সনাতন পদার্থবিদ্যা পড়ি আমরা, বা যেসব অঙ্ক কষি, তার মধ্যে একটা প্রতিশ্রুতি থাকে। একটা বস্তুর শুরুর অবস্থান আর গতিবেগ জানলে এবং সেটার উপর কোন কোন বল কাজ করছে সেইটা জানলে, বস্তুটার যেকোনো সময়ে অবস্থান বলে দেওয়া যায়। তারপর অঙ্কটা কষে ল্যাবে গিয়ে পরীক্ষা করে দেখা যায়, যে উত্তরটা পেয়েছিলাম, তার মোটামুটি কাছাকাছিই থাকছে বস্তুটা। 

যেমন, একটা পেন্ডুলাম।

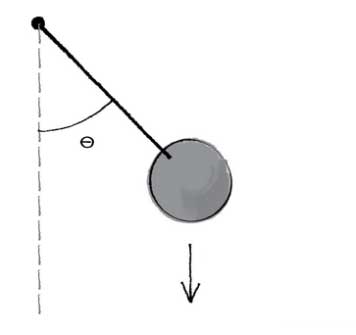
নিচের বলটাকে একটা বিশেষ কোণে-এ ছাড়লে কিছুক্ষণ পর কোথায় থাকবে নিউটনের সূত্র ব্যবহার করে অঙ্ক কষে বলে দেওয়া যায়। তারপর যদি সত্যিই ওই কোণে ছাড়ি, ওই সময় পর দেখা যাবে বলটা মোটামুটি অঙ্কে পাওয়া অবস্থানেই আছে। এই প্রতিশ্রুতির উপর দাঁড়িয়ে আছে সনাতন পদার্থবিদ্যার ভিত। অঙ্কের উত্তরগুলো শুধু খাতায় কলমে নয়, বাস্তব জগতেও খাটে। 

পরিমাপের সীমাবদ্ধতা

উপরের কথাটার মধ্যে মোটামুটি শব্দটা ব্যবহার করলাম কারণ বাস্তব পরীক্ষা করার সময় আমি শুরুর অবস্থানটা অত নিখুঁতভাবেও ঠিক করে দিতে পারবো না। একটু “ভুল” থেকেই যায়।

ধরো, চাঁদা দিয়ে পেন্ডুলাম ছাড়ার কোণটা মাপলাম। 

ধরো, এক ডিগ্রীর কম সেই চাঁদাতে মাপা যায় না। যখন বলছি, তিরিশ ডিগ্রীতে ছাড়লাম, হয়তো সেটা 30.1 ডিগ্রী। সেই ভুলের ফলে শেষের অবস্থানটাও একটু পাল্টে যেতে পারে। 

কিন্তু তাতে ততটা যায় আসে না কারণ ওই শুরুর ভুলটা সামান্য হলে শেষের অবস্থানেও সামান্যই এদিক ওদিক হয়। এমনকি, শুরুর ওই সামান্য ভুলটা কতটা হতে পারে, তার একটা আন্দাজ থাকলে এটাও বলা যায় যে শেষের বস্তুটা অমুক জায়গা থেকে অমুকের মধ্যে থাকবে। অর্থাৎ, অঙ্কে পাওয়া ফলাফলের কতটা দূরের মধ্যে থাকবে, সেইটা বলা যায়। 

যেমন, উপরের কেসটাতে জানি যে শুরুতে এক ডিগ্রি মত গলদ থাকতে পারে। ওই এক ডিগ্রী গলদের কারণে কিছুক্ষণ পর পেন্ডুলামের অবস্থানে কতটা গলদ দেখা দেবে, সেইটা কষে দেওয়া যায়।

ক্যাওটিক সিস্টেম (chaotic system)

এই কথাগুলো উপরের পেন্ডুলাম এর মত সিস্টেম-এর ক্ষেত্রে খাটে। ইস্কুলের পাঠ্যবইয়ে এই ধরণের সিস্টেম নিয়েই কাজ করে থাকি আমরা। কিন্তু কিছু সিস্টেম-এর ক্ষেত্রে একটা অদ্ভুত ব্যাপার ঘটে। ওই উপরের পেন্ডুলামটাকেই আরেকটু জটিল করা যাক। প্রথম পেন্ডুলামটার নিচে একটা দ্বিতীয় পেন্ডুলাম লাগিয়ে দেওয়া যাক। এটাকে বলে ডাবল পেন্ডুলাম। শুরুর প্রশ্নটাতে যে ব্যবস্থাটা দেখানো হয়েছে সেটা একটা ডাবল পেন্ডুলাম-এরই বাস্তবায়ন।

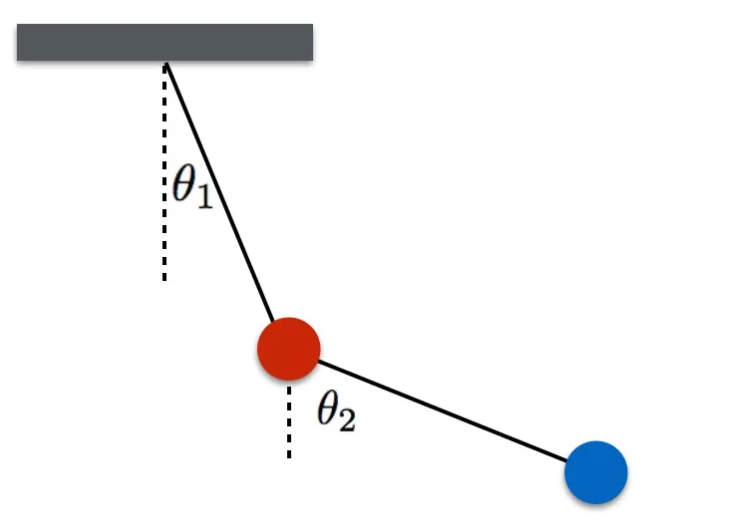
এই ডাবল পেন্ডুলাম-কে অল্প কোণে ছাড়লে সেটার চলন হবে এইরকম:

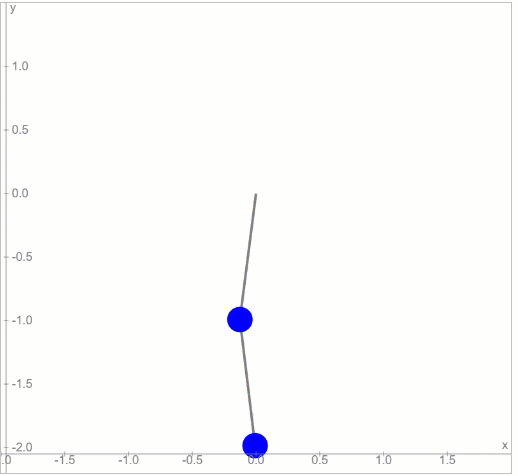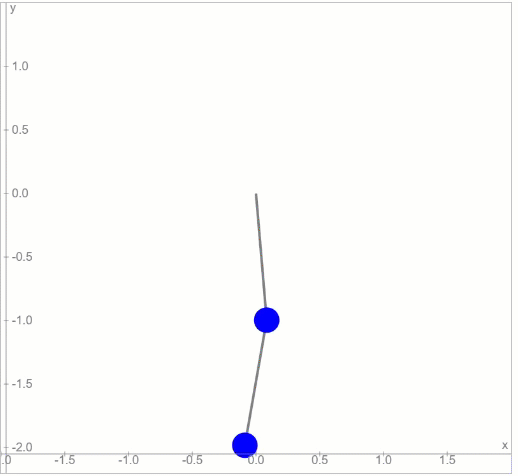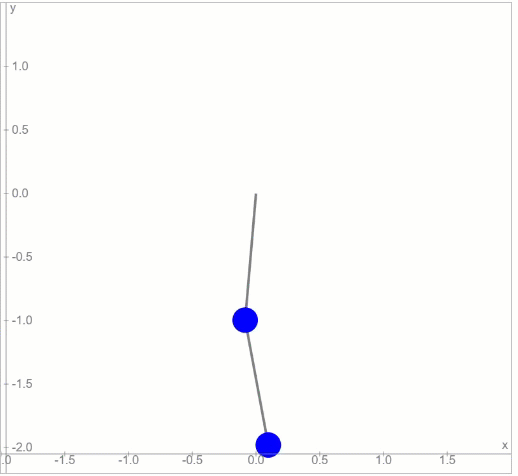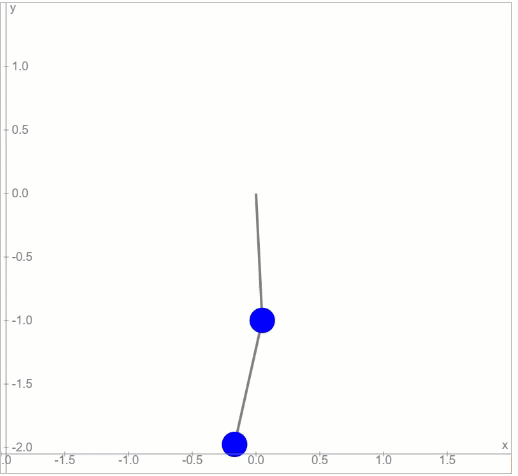
দুটো সিম্পল পেন্ডুলাম, একটার নিচে আরেকটা থাকলে যেরকম হওয়া উচিত, এই চলনটা অনেকটা সেরকমই। কিন্তু মুশকিল হবে এই পেন্ডুলাম-টাকে বড় কোণে ছাড়লে। তখন চলনটা হবে এইরকম:

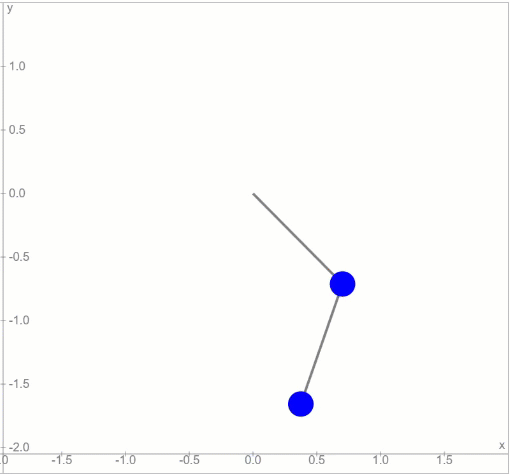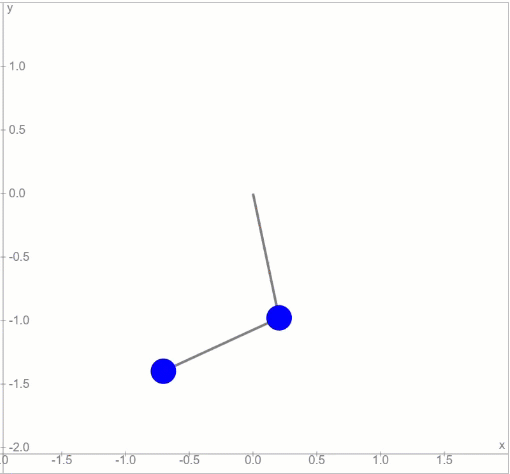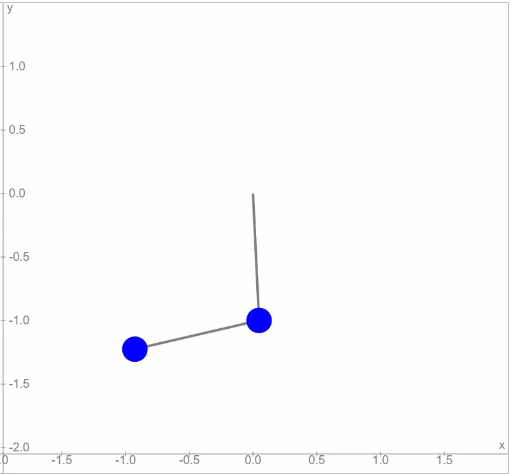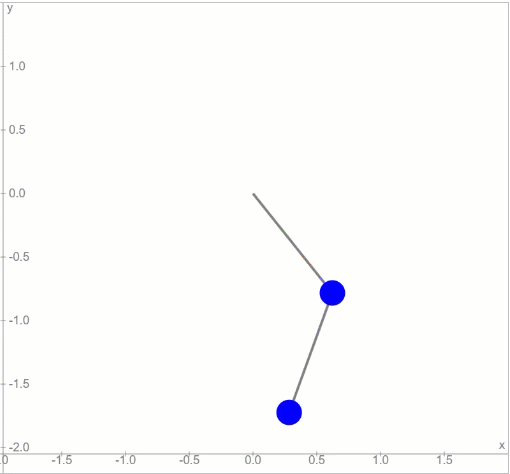
এইবার পড়বে ফ্যাসাদে। শুরুর অবস্থায় একটু ভুল হলেই আর বলতে পারবে না, কিছুক্ষণ পর দ্বিতীয় পেন্ডুলাম এর নিচে ঝুলন্ত বস্তুটাকে কোথায় পাওয়া যাবে। ফলে অঙ্কের সাথে বাস্তবের মিল পাওয়া দুরূহ ব্যাপার হয়ে দাঁড়াবে। 

শুধু তাই না, বাস্তবেও প্রত্যেকবার পেন্ডুলাম-টাকে আপাতদৃষ্টিতে একই জায়গা থেকে ছাড়লেও আগের থেকে এক্কেবারে আলাদা আচরণ দেখতে পারো। নিচের ছবিটার মতো। তিনটে ডাবল পেন্ডুলামকে প্রায় একই জায়গা থেকে শুরু করিয়ে সময়ের সাথে তাদের চলাফেরা দেখা হচ্ছে।

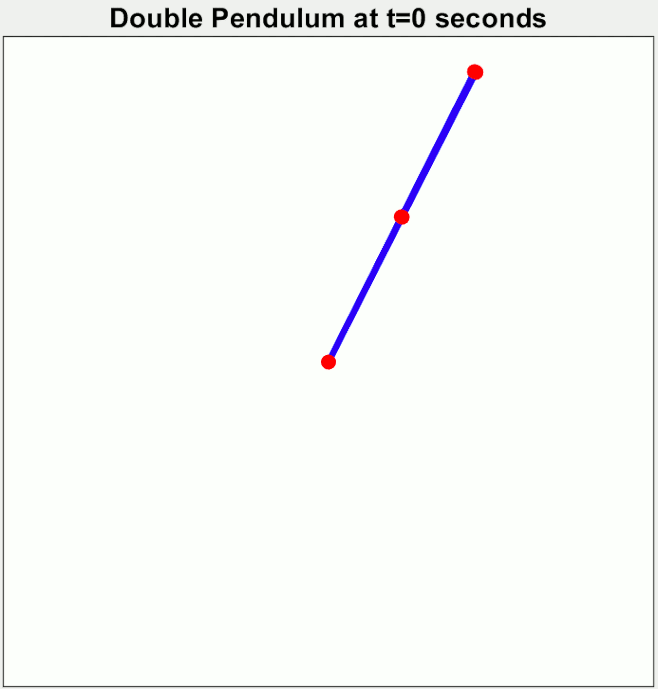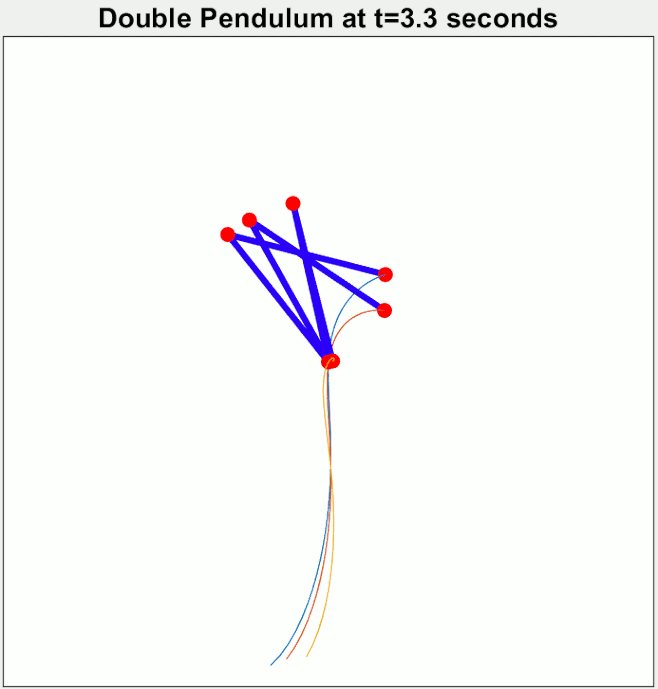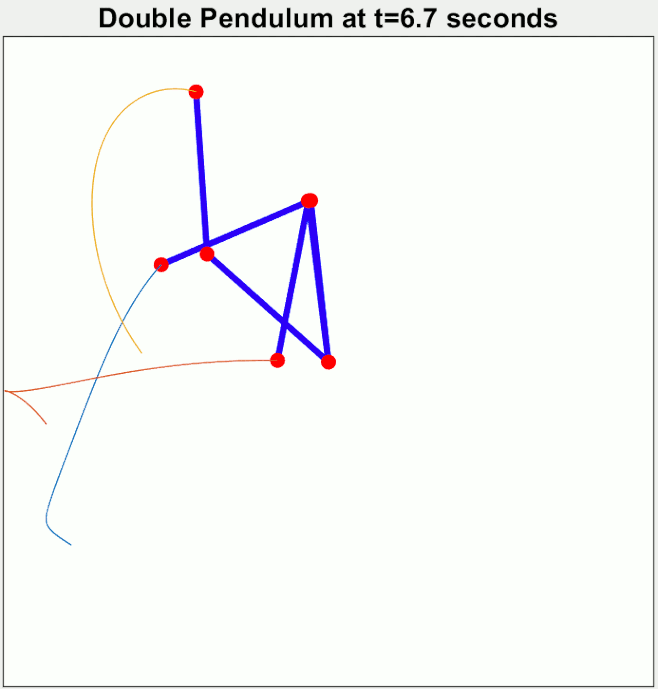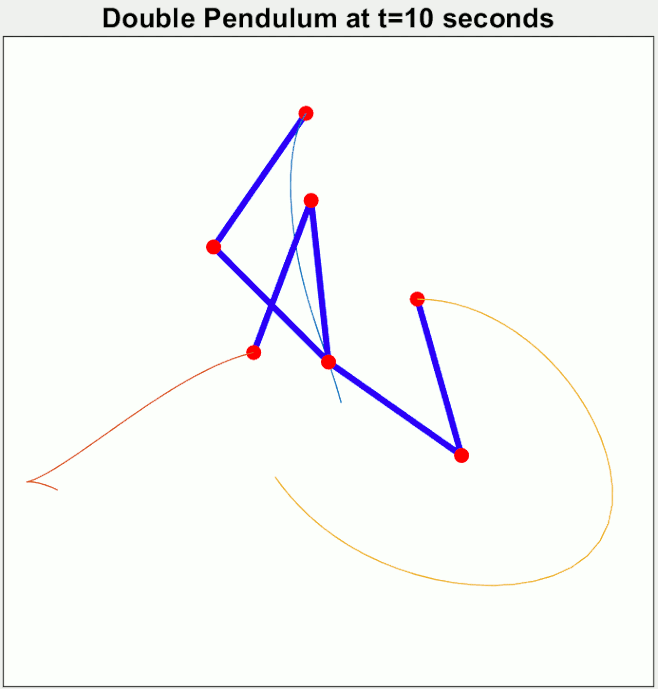
দেখা যাচ্ছে অচিরেই তাদের চলাফেরা একে অপরের থেকে এতটাই আলাদা হয়ে যাচ্ছে যে শুরুতে তারা যে কাছাকাছি ছিল তার কোনো পরিচয় আর দেখা যাচ্ছে না।

এরকমটা কেন?

এক ধরণের সিস্টেম হয় যেগুলোর শুরুর অবস্থার যৎসামান্য পরিবর্তন হলেই বস্তুর চলপথ রাতারাতি পাল্টে যায়। উপরের ডাবল পেন্ডুলাম সেই গোত্রেরই সিস্টেম।

যেহেতু বাস্তবে শুরুর অবস্থাটা প্রত্যেকবার একইরকম করতে পারছি না, একটু উনিশ বিশ থেকেই যায়, তাই এই ধরনের সিস্টেম-এর জন্য প্রত্যেকবার আলাদা আলাদা চলপথ পাওয়ার সম্ভাবনা থাকে। আর অঙ্কের সাথেও মেলে না কারণ শুরুর অবস্থাটাকে অঙ্কে যা ধরেছিলাম, বাস্তবে একদম সেই মানেই শুরু করা যায় না (অর্থাৎ, দশমিকের পর সব সংখ্যাকে অঙ্কের মানে রাখা সম্ভব না)।

এই ধরনের সিস্টেমগুলোকে বলে ক্যাওটিক সিস্টেম (chaotic system)। একটা সিস্টেমকে ক্যাওটিক হতে গেলে তার কিছু বিশেষত্ত্ব থাকতে হয়, নইলে এরকম আচরণ দেখা সম্ভব নয়। যেমন, এদের চলার সমীকরণগুলো (equations of motion) অরৈখিক (nonlinear) হয়, অর্থাৎ সমীকরণে সবকটা রাশিকে একই গুণিতক দিয়ে বাড়ালে, গোটা সমীকরণটাই সেই গুণিতকে বাড়ে না। সমীকরণ শুধু অরৈখিক হলেই চলবে না, শুরুর অবস্থার উপর এই মারাত্মক নির্ভরতা দেখতে হলে আরো কিছু বিশেষত্ত্ব থাকতে হবে।

কিন্তু মোদ্দা কথা হলো, ক্যাওটিক সিস্টেম-এ শুরুর অবস্থার এত্তোটুকু পরিবর্তন হলেই বস্তুর চলপথ খুব তাড়াতাড়ি দিন থেকে রাত হয়ে যেতে পারে। এই ধারণাটা নিয়ে একটা মজার চলচ্চিত্র হয়েছে : জার্মান ভাষার Run Lola Run। তাতে একই ঘটনা তিনবার দেখানো হয়েছে, শুধু শুরুতে উনিশ বিশ তফাৎ। সেই সামান্য তফাত থেকেই একবার লোলা তার বয়ফ্রেন্ডকে বাঁচাতে গিয়ে প্রাণ দেয়, তো আরেকবার বাঁচানোর প্রয়োজনও পড়ে না।

কম্পিউটারের প্রিসিশন (precision) এর উপর যখন উত্তর নির্ভর করে 

শুধু বাস্তবে না, কম্পিউটার সিমুলেশন-এও এই সমস্যাটা দেখা যায়। কম্পিউটার কতটা প্রিসিশন (precision) সহ অঙ্ক কষছে, তার উপর নির্ভর করে ডাবল পেন্ডুলাম-এর চলাটা কীরকম হবে। 

কম্পিউটারে গণনার সময় যেহেতু সীমিত সংখ্যক বিট নিয়ে কাজ করা হয়, তাই কম্পিউটার বাবাজি গণনার একেকটা স্তরে কিছুটা “ভুল” করে। অর্থাৎ, দুপুর বারোটায় বস্তুটা কোথায় আছে, সেটা থেকে যখন বারোটা বেজে এক সেকেন্ড পরে বস্তুটার অবস্থা গণনা করতে যায়, কম্পিউটার দশমিকের পর কয়েকটা সংখ্যা রেখে বাকিটা ঝেড়ে ফেলে। যেমন, হতে পারে বস্তুটার অবস্থান 1.00000000000000124… মিটার দূরে, কম্পিউটার সেটাকে ধরে 1.00000000000000।

এমনিতে এতে কোনো ঝামেলা হবে না কিন্তু এই ধরণের ক্যাওটিক সিস্টেম তো শুরুর ভুল-এর উপর মারাত্মকভাবে নির্ভরশীল। তাই, শুরুর ওই সামান্য ভুলের ফলে অচিরেই ভুলের পাহাড় হয়ে যায়। এবং কম্পিউটার ডেসিমাল-এর পর যত বেশি সংখ্যা নিয়ে কাজ করতে পারবে, অর্থাৎ যত বেশি প্রিসিশন হবে, তত শুরুর ভুলটা কম হবে। তাই কীরকম কম্পিউটারে সিমুলেশন করছি, তার উপর নির্ভর করে একটা ক্যাওটিক সিস্টেম-এর চলনটাই পাল্টে যায়।

এই শুরুর অবস্থার উপর অতিনির্ভরতাকে অঙ্কে দেখতে চাইলে খুব সহজ কিছু অঙ্ক কষা যায়। ডাবল পেন্ডুলাম-এর চলনের থেকেও সহজ। সেরকমই একটা অঙ্ক কষে দেওয়া হয়েছে এখানে : বিশৃঙ্খলার গতিবিদ্যা। 

আমরা আগেই দেখেছি, আবহাওয়ার পূর্বাভাসের মত বেশ কিছু ক্ষেত্রে এই ক্যাওটিক আচরণ দেখা যায়। সুদূর আবহাওয়ার পূর্বাভাস এতো কঠিন কারণ আবহাওয়ার মডেল করতে যে সমীকরণগুলো ব্যবহার করা হয়, তার সমাধানেও শুরুর অবস্থার উপর অতিনির্ভরতা দেখা যায়। তাই কম্পিউটারের যত বেশি প্রিসিশন, তত দূরের আবহাওয়া ঠিকঠাক বলা সম্ভব। একসময় যতটা সঠিকভাবে বলা যেত, এখন তার থেকে বেশি বলা যায়, কারণ কম্পিউটারের ক্ষমতা বেড়েছে।

এই যদি হয় ক্যাওসের নমুনা, তাহলে আশা করা উচিত নয় যে দুটো ক্যাওটিক সিস্টেম একে অপরের সান্নিধ্যে এলে তালে তাল মেলাবে। যেমনখুশি আচরণ সত্ত্বেও এ যেমন চলবে, ও-ও তেমনি চলবে। কিন্তু এরকমটাই দেখানো গেছে এক পরীক্ষায়, এবং এই পরীক্ষার ফলে ক্যাওস-কে বাগে আনবার একটা উপায় পাওয়া গেছে। সেই গল্প জানতে হলে অন্য একটা পর্বের জন্য অপেক্ষা করতে হবে। কিম্বা নিচের ভিডিও-টাও দেখতে পারো। শুধু ক্যাওটিক সিস্টেম নয়, এই তালে তাল মেলানো বা সমলয়ন আর কোথায় কোথায় দেখা যায়, সব জানতে পারবে! 

Cover image credit – Pinterest