ওজনদার বস্তুর উপর জমির “প্রতিক্রিয়া”
টেবিল-এর ওপর একটা বই রাখো। যদি জিজ্ঞেস করি বইটার ওপর কোন কোন বল কাজ করছে, চট করে বলে দেবে, বইয়ের ওজন-টাকে সামাল দিচ্ছে টেবিলের প্রতিক্রিয়া। যেটাকে প্রতিক্রিয়া বললে, সেটা নিশ্চয় ওজনের প্রতিক্রিয়া না। কারণ নিউটনের তৃতীয় সূত্রের ক্রিয়া-প্রতিক্রিয়া তো আলাদা বস্তুর ওপর কাজ করে, এখানে দুটোই কাজ করছে ওই বইটার ওপর। তাহলে টেবিলের “প্রতিক্রিয়া” আবার কি?
আসলে একটা উপরিতল-কে (surface) যতই মসৃণ লাগুক, মাইক্রোস্কোপ দিয়ে দেখলে আর মসৃণ থাকে না। যেটাকে মসৃণ মনে হচ্ছিলো, সেটাই একগুচ্ছ পাহাড় আর মাঝের উপত্যকায় পরিণত হয়। অতএব, যখন বইটা টেবিলের ওপর রাখা হয়, বইয়ের কিছু অণুর সাথে টেবিলের কিছু অণুর ঘষাঘষি লাগে (চিত্র ১ দেখো)।
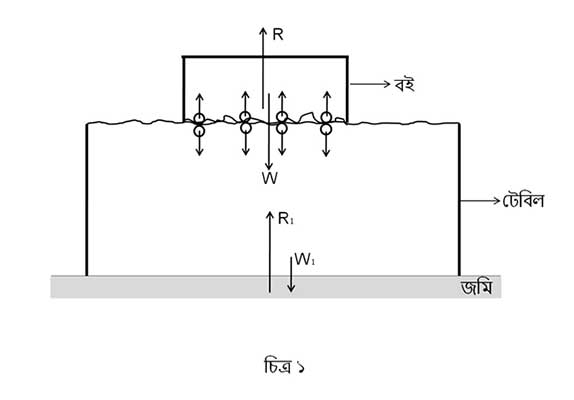
অণুগুলোর ধর্ম হলো এইরকম: তাদের পারস্পরিক দূরত্ব equilibrium বা সাম্যাবস্থার দূরত্বের থেকে কমে গেলে তারা একে অপরকে ঠেলতে থাকে আর দূরত্ব বেড়ে গেলে টানে। অর্থাৎ, তারা স্বাভাবিক অবস্থায় ফেরৎ যেতে চায়। বইয়ের অণুগুলো মাধ্যাকর্ষণের টানে নিচে যাওয়ার চেষ্টা করে, তারা টেবিলের অণুর সংস্পর্শে থাকার ফলে তাদেরও নিচের দিকে ঠেলে। টেবিলের অণুগুলোও ফিরে আসার চেষ্টা করে তাদের স্বাভাবিক অবস্থায় এবং জন্ম হয় নতুন এক প্রতিক্রিয়ার। সবকটা অণুর প্রতিক্রিয়া জুড়লে (resultant) বইয়ের উপর যে বলটা তৈরী হয়, সেটা স্বাভাবিকভাবেই সরাসরি উপরের দিকে। এটাকেই গোদা ভাষায় “টেবিলের প্রতিক্রিয়া” হিসেবে চিহ্নিত করা হয়। স্বাভাবিক অবস্থায়, যখন কেউ নড়ছে-চড়ছে না, তখন এই টেবিলের প্রতিক্রিয়া (ধরা যাক, 
এতক্ষণ বইটার কথা ভাবছিলাম। বইটা ছেড়ে যদি এবার টেবিলটাকে দেখি, সেও তো নড়ছে না। তার ওজন যদি হয় 
আর যেহেতু বইয়ের ওজনের সমান, তাই:
বই আর টেবিলটাকে মিলে যদি একটা বস্তু ভাবি, তাহলে উপরের সমীকরণটা সেই বস্তুটার জন্য প্রযোজ্য। অর্থাৎ, বই এবং টেবিলের মিলিত ওজন জমির প্রতিক্রিয়ার সমান। আরেকবার বলি, এই “জমির প্রতিক্রিয়া”-কে ব্যাখ্যা করতে হলে আণবিক স্তরে যেতে হবে। যেভাবে একটু আগে “টেবিলের প্রতিক্রিয়া”-কে বোঝালাম।
ঝুলন্ত বস্তু যে টান অনুভব করে
ধরা যাক, সিলিং থেকে সুতো দিয়ে ঝুলছে একটা বস্তু। বস্তুর ওজন
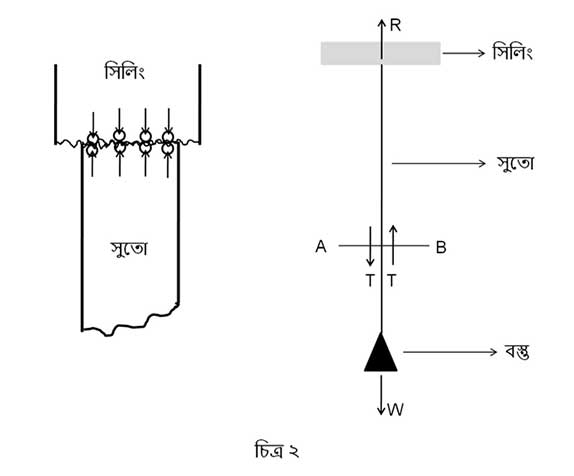
তখন তুমি বলবে যে সিলিং-এর “প্রতিক্রিয়া”
এবার AB বরাবর সুতোর একটা প্রস্থচ্ছেদ (cross-section) কল্পনা করো। যেহেতু সিলিং-সুতো-ঝুলন্তবস্তু মিলিয়ে গোটা সিস্টেম-টা সাম্যাবস্থায় রয়েছে (equilibrium), একেকটা অংশও তাই। অর্থাৎ এই প্রস্থচ্ছেদের উপরের আর নিচের অংশটাও আলাদা করে সাম্যাবস্থায় রয়েছে। এই অংশবিশেষের সাম্যাবস্থাকে কিভাবে বোঝানো যায়? গোটা বস্তুটা সাম্যাবস্থায় রয়েছে মানে তার ওপর নিচের দিকে আর উপরের দিকের বল সমান। এবার তাতে যদি একজোড়া নতুন বল জুড়ে দি, যেগুলো সমান এবং বিপরীতমুখী, কিছু যায় আসবে না। তখনো নিম্নমুখী আর ঊর্ধ্বমুখী বল সমান থাকবে।
উপরের ছবিতে তাই করা হলো। ধরা যাক ওই প্রস্থচ্ছেদের নিচের অংশটাকে একটা বল টানছে আর উপরের অংশটাকে একই পরিমাণ বল ঠেলছে, এবং উভয় বলের মান 
যদিও ‘টান’ নামক বলটা অংশবিশেষের সাম্যাবস্থা বোঝাতে আমদানি করলাম, এই টান-এর ধারণাটা আকাশ থেকে পড়েনি, এর উৎসও আণবিক স্তরে। আগেই বলেছি যে বস্তুর মধ্যের অণুগুলো পরস্পরের থেকে দূরে সরে গেলে, তারা সেই দূরত্বকে স্বাভাবিক অবস্থায় ফিরিয়ে নিয়ে যেতে চেষ্টা করে। অর্থাৎ সুতোর উপরের অংশের আর নিচের অংশের অণুগুলো পরস্পরকে টানে। এই আণবিক বলগুলোকে জুড়লে দেখা যায় যে সুতোর উপরের অংশের ওপর নিট বল কাজ করছে নিচের দিকে, আর নিচের অংশের ওপর বলটা উপরের দিকে। এটাই টান।
টান কতটা, সেটা কি সুতোর সর্বত্রই সমান? যদি সুতোর কোনো ওজন না ধরি, তাহলে সেই ওজনের বল নিয়ে মাথা ঘামাতে হচ্ছে না। সুতোর যেখানেই প্রস্থচ্ছেদ কাটি না কেন, প্রস্থচ্ছেদ-এর নিচের অংশটাকে ধরলে টান খালি নিচের বস্তুর ওজনটাকে সামাল দেয়, সুতোর কোনো ওজন নেই। অর্থাৎ, সর্বত্রই লেখা যায় 
কিন্তু সুতোর যদি একটা ওজন থাকে, তখন কিন্তু আর সুতোর সর্বত্র একই টান থাকবে না? কোনো একটা জায়গায় টান কতটা, সেটা কিভাবে বার করা হবে তখন? সেই গল্প পরের পর্বে।
(লেখাটা মূল ইংরেজি থেকে বাংলায় অনুবাদ করেছে ‘বিজ্ঞান’ টীম-এর অনির্বাণ গঙ্গোপাধ্যায়।)
ছবি: ধীরঞ্জন রায় / বনানী মণ্ডল