টিফিনের পর পরাণমাস্টার অঙ্কের ক্লাসে ঢুকে ছাত্রদের বললেন, “বুঝলি, ভাবছি এবারের ফাইনাল পরীক্ষায় একটা মজা করব। দশ নম্বরের প্রশ্নের সঠিক উত্তর লিখলে শুধু সাত পাবি। বাকি তিনটে নম্বর পাওয়ার জন্যে উত্তরটাকে সুন্দরও হতে হবে।”
টিফিনের পর সবারই বেশ ঘুম ঘুম পাচ্ছিলো। এমনকি ক্লাসের ফার্স্টবয় গোপালও জেগে থাকার জন্যে নিজেকে চিমটি কাটছিলো মাঝে মাঝে। এসবের মধ্যে পরাণমাস্টারের এই পিলে চমকানো কথা শুনে সবাই একটু নড়েচড়ে বসলো। যদিও পরাণ এরম কথা মাঝে মাঝেই বলে থাকে। লোকটার আজগুবি কথা বলা আর বাড়িয়ে বলা এই দুটো বদঅভ্যেসই আছে। মাথায় একটু ছিট থাকলে যেরম হয় । তাই এসব শুনে ছেলেরা অতটাও ভয় পায় না আজকাল। পরাণ সাসপেন্স ক্রিয়েট করার জন্য একটু থামলেন। কিন্তু কেউ বিশেষ পাত্তা দিলো না দেখে একটু ক্ষুণ্ণ হয়েই আবার শুরু করলেন, “ধর একটা ত্রিভুজ আছে।” বলে ব্ল্যাকবোর্ডে আঁকলেন:
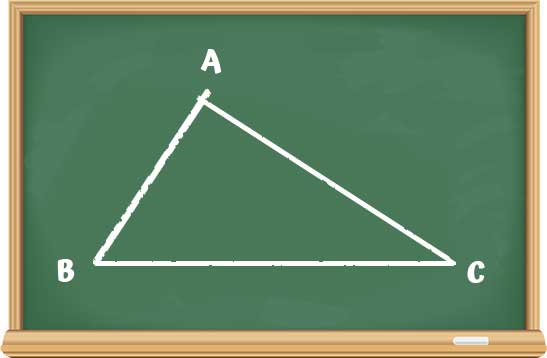
“আমরা শিখেছি যে এর তিনটে কোণের সমষ্টি ১৮০ ডিগ্রী।”
“এটা কেন হয় তোদের দেখিয়েছিলাম। মনে আছে?”
যথারীতি গোপালের মনে ছিল। সে ব্ল্যাকবোর্ডে গিয়ে প্রমাণটা দেখালো।
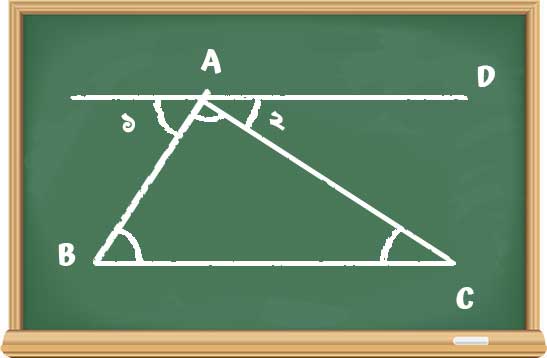
“ ” বিন্দুর মধ্যে দিয়ে
-র সমান্তরাল একটা রেখা (
) আঁকলাম। সমান্তরাল রেখার ধর্ম থেকে আসে:
১ ,
২ ,
আবার এক সরলরেখার ওপর অবস্থিত বলে:
১
২
এই দুটো সিদ্ধান্ত একত্র করলে ত্রিভুজের আলোচ্যমান ধর্মটা আসে।”
“বেড়ে বলেছিস!” পরাণ আবার শুরু করলেন, “এবার বলতো এই বহুভুজটার সবকটা কোণের যোগফল কত?” বলে ব্ল্যাকবোর্ডে এটা আঁকলেন:
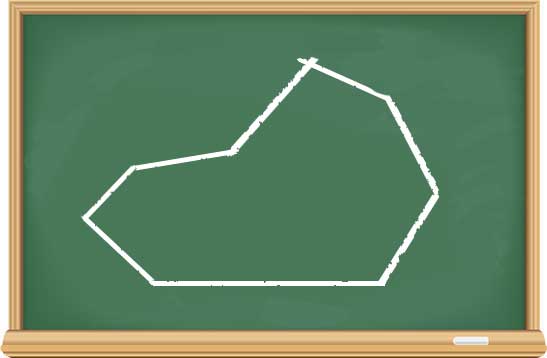
এবার যে কজন মন দিয়ে শুনছিলো তারা সবাই ভ্যাবাচ্যাকা। খালি গোপাল চাপ নিয়ে খাতায় অনেক আঁকিবুকি কাটলো:
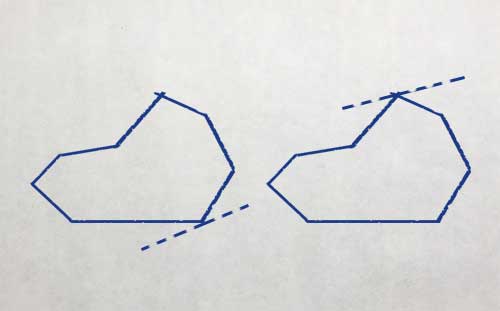
কিন্তু কোন শীর্ষবিন্দু দিয়ে যে সমান্তরাল রেখা টানবে আর কোন বাহুর সাথেই বা সেটা সমান্তরাল হবে তার মাথামুন্ডু খুঁজে পেলো না।
পরাণ মুচকি মুচকি হাসছেন এমন সময় পেছন থেকে দুর্গার মিনমিনে গলা শোনা গেলো, “আচ্ছা বহুভুজটাকে অনেকগুলো ত্রিভুজে ভেঙে ফেললে হয় না ?”
দুর্গার মিনমিনে গলা শোনা গেলো, “আচ্ছা বহুভুজটাকে অনেকগুলো ত্রিভুজে ভেঙে ফেললে হয় না ?”
পরাণ একটু অবাক হলেন। মন্দ বলেনি মেয়েটা!
“দেখা কিভাবে ভাঙবি।” পরাণের ক্লাসে ব্ল্যাকবোর্ডে সবার অবাধ গতিবিধি ছিল। দুর্গা বোর্ডে এসে এই লাইনগুলো আঁকলো
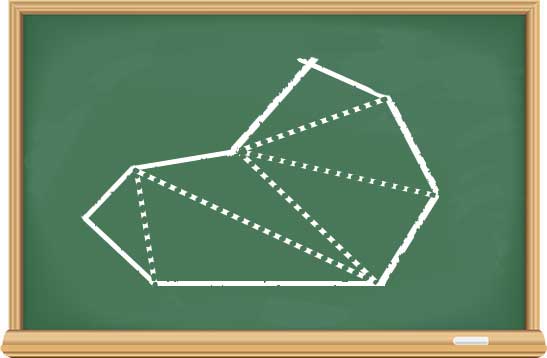
তারপর বললো, “বহুভুজের কোণগুলোর যোগফল ওই ছ’ টা ত্রিভুজের কোণগুলোর যোগফলের সমান। একেকটা ত্রিভুজ থেকে আসে ১৮০ ডিগ্রী, সুতরাং মোট কোণের পরিমাণ হলো ১৮০ x ৬ = ১০৮০ ডিগ্রী।”
“একদম সঠিক!”
দুর্গা বেঞ্চে ফেরত গেলে পরাণ আবার শুরু করলেন, “এটা খুবই ভালো সমাধান, কিন্তু আরও ভালো হতো যদি আমাদের শুরুর যুক্তিটা, যেটা দিয়ে ত্রিভুজের ধর্মটা প্রমাণ করেছিলাম সেটা যেকোনো বহুভুজের ক্ষেত্রেই লাগানো যেত, তাই না?”
এই বলে ত্রিভুজের ছবিটায় ফেরত গিয়ে গোপাল যে লেজুড় গুলো জুড়েছিলো সেগুলো মুছে ফেললেন।

“ধর আমি ত্রিভুজের বাহু বরাবর হাঁটতে থাকলাম: প্রথমে থেকে
, তারপর বাঁক নিয়ে
থেকে
, আবার বাঁক নিয়ে
থেকে
, শেষ বাঁক নিয়ে আবার
রাস্তায় ফেরত।”
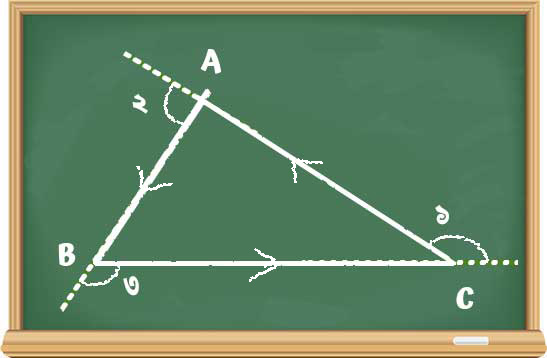
“অর্থাৎ আমি শুরুতে যেমুখো যাচ্ছিলাম, এক চক্কর মেরে আবার সেইদিকেই যেতে শুরু করলাম। সুতরাং আমার তিনটে বাঁকের ( ১,
২, আর
৩) সমষ্টি হলো একটি পূর্ণকোণ বা ৩৬০
।”
১ +
২ +
৩ = ৩৬০
“ত্রিভুজের কোণগুলির সাথে এই বাঁকের কোণগুলির (যাদেরকে ত্রিভুজের বহির্মুখী কোণ বলতে পারি) একটা সোজাসুজি সম্পর্ক আছে:”
২
৩
১
“এই দুটো তথ্য থেকে আসে:”
“কেমন লাগলো যুক্তিটা?”
কেউ কিছু না বললেও কয়েকজনের মাথা নাড়া থেকে বোঝা গেলো তাদের ভালো লেগেছে।”
“দুটো প্রমাণই সঠিক”, পরাণমাস্টার বলে চললেন, “কিন্তু নতুন প্রমাণটা বেশ সুন্দর লাগলো না? লাগলো কি?”
অনেকেই আবার উপরনিচে মাথা নাড়লো।
“কেন লাগলো বলতে পারবি?”
পেছনের বেঞ্চ থেকে দুর্গা মাথা চুলকে বললো, “বইয়ের প্রমাণটায় কথা নেই বার্তা নেই কিরম দুম করে একটা সমান্তরাল রেখা টানতে বললো। এটা মূখস্থ করে রাখতে হবে — নইলে মনে থাকবে না। সেই তুলনায় ত্রিভুজের রাস্তা ধরে হাঁটলে যে পুরো একপাক ঘোরা হয় এটা বেশ মজার জিনিস। নতুন প্রমাণটায় একটা সুন্দর গল্প আছে।”
বইয়ের প্রমাণটায় কথা নেই বার্তা নেই কিরম দুম করে একটা সমান্তরাল রেখা টানতে বললো। এটা মূখস্থ করে রাখতে হবে — নইলে মনে থাকবে না। … নতুন প্রমাণটায় একটা সুন্দর গল্প আছে।
“ভালো বলেছিস!” পরাণ খুশি হলেন, “ওটাই নতুন প্রমাণটার আইডিয়া। আর শুধু ত্রিভুজ নয়, সমতলে যেকোনো সহজ বদ্ধ বক্ররেখার (simple closed curve) জন্যেই এ কথাটা খাটে। অর্থাৎ বক্ররেখাটাকে শেষে এসে নিজের সাথে মিলিত হতে হবে (বদ্ধ), আর মাঝে নিজেকে কোথাও ছেদ করা চলবে না (সহজ)। রেখাটা পুরোটাই বাঁকানো হওয়ার প্রয়োজন নেই — টুকরো টুকরো সরলরেখা জুড়ে বানালেও চলবে। এই হিসেবে আমাদের ত্রিভুজও একটা সরল বদ্ধ বক্ররেখা। অর্থাৎ এই রেখাগুলোর জন্য আমাদের যুক্তিটা খাটবে:

কিন্তু এইগুলোর জন্য খাটবে না:
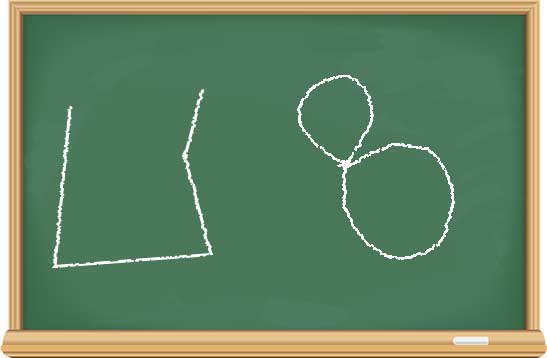
খালি দুটো কথা মনে রাখতে হবে:
- রেখাটা বহুভুজ না হলে বাঁকগুলো দুম দুম করে ৩-৪ টে জায়গা হয়না – ক্রমাগত একটু একটু করে হতে থাকে। এক্ষেত্রে মোট বাঁকের হিসেব করাটা একটু কঠিন – তার জন্যে ক্যালকুলাস বা কলনবিদ্যার প্রয়োগ করতে হয়। কিন্ত আমাদের মূল আইডিয়া টা তখনো ঠিক – মোট বাঁকের পরিমাণ এক পূর্ণকোণ বা ৩৬০ ডিগ্রী।
- একটা বাঁক কোনদিকে হচ্ছে – ঘড়ির কাঁটা যেদিকে ঘোরে সেইদিকে (দক্ষিণাবর্ত/clockwise) না তার উল্টোদিকে (বামাবর্ত/anticlockwise) তার খেয়াল রাখা প্রয়োজন। আমাদের ত্রিভুজের উদাহরণে তিনটে বাঁক-ই বামাবর্ত ছিল। কিন্তু এই বহুভুজটায় একটা বাঁক দক্ষিণাবর্ত। যোগ করার সময় বামাবর্ত বাঁক-কে ধণাত্মক ধরলে দক্ষিণাবর্ত বাঁক-কে ঋনাত্বক ধরতে হবে।”
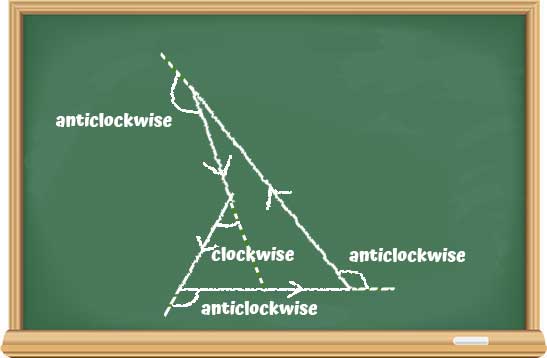
“এই ফাঁকে তোদের একটু জ্ঞান দিয়ে দি। সাধারণতঃ আমরা গণিতজ্ঞরা একটা বিষয়ে মোটামুটি একমত: যে কোনো একটা যুক্তি যত সরল, সেটা তত বেশি সুন্দর। প্রচুর কায়দা আর মারপ্যাঁচ ওয়ালা যুক্তি আমরা ততটা পছন্দ করি না। সেই অর্থে আমাদের নতুন প্রমাণটা আগেরটার থেকে বেশি সুন্দর, যদিও দুটোই একদম সঠিক।”
গণিতজ্ঞরা একটা বিষয়ে মোটামুটি একমত: যে কোনো একটা যুক্তি যত সরল, সেটা তত বেশি সুন্দর।
“সরল প্রমাণ ভালো লাগার একটা কারণ হলো অনেক সময়েই তার থেকে আমরা বিষয়টা সম্বন্ধে বেশ গভীর কিছু অন্তর্দৃষ্টি পাই। যেমন এখানে শুরুতে আমরা মাথা ঘামাচ্ছিলাম ত্রিভুজের ভেতরের কোণগুলো নিয়ে, কিন্তু শেষে দেখলাম যে ত্রিভুজের বাইরের কোণগুলোর যোগফল আরও মৌলিক একটা ধর্ম। কারণ সেটা শুধু যেকোনো ত্রিভুজ নয়, যেকোনো সরল বদ্ধ বক্ররেখার ক্ষেত্রেই সবসময় এক পূর্ণকোণ হয়। আর তার কারণ ঐরকম একটা রেখা মোট একপাক ঘুরে আবার নিজেতে ফিরে আসে!”
“এছাড়া আরও একটা ব্যাপার আছে: সেটা হলো প্রতিসাম্য। এখানে আমরা বার করতে চাইছি . আমাদের প্রশ্নটাতে ,
আর
তিনটে শীর্ষবিন্দুই সমান গুরুত্বপূর্ণ। কিন্তু প্রথম প্রমাণটায়
বিন্দুটাকে আলাদাভাবে দেখা হচ্ছে
আর
-এর থেকে। সেটা করা মোটেই ভুল কিছু না, কিন্তু এরকম একটা যুক্তি গণিতজ্ঞদের সৌন্দর্যবোধে একটু খোঁচা দেয়। যেন তিনটে বিন্দুকে সমানভাবে ব্যবহার করে একটা যুক্তি খাড়া করতে পারলে আরেকটু ভালো হতো। আমাদের দ্বিতীয় প্রমাণটা আশাটা পূর্ণ করে।”[1]
“এর থেকে বহুভুজের প্রশ্নটার সমাধান করা তো জলভাত। এটা তোদের হোমওয়ার্ক।” বলে পরাণ গটগট করে বেরিয়ে গেলেন। ক্লাস শেষের ঘন্টাও বাজলো।
উৎসাহী পাঠকদের জন্য
[১] Measurement, Paul Lockhart, Harvard University Press (2012)
[২] Proofs from THE BOOK, Martin Aigner, Gunter M Zeigler, Karl H Hoffman, Springer (2013)
~প্রচ্ছদের ছবির উৎস : https://pixabay.com/
[1] বিখ্যাত গণিতজ্ঞ পল এরদিশ মাঝে মাঝে (খানিকটা মজা করেই) বলতেন যে ঈশ্বরের কাছে একটা বই আছে যাতে যাবতীয় গাণিতিক উপপাদ্যের সবচেয়ে সুন্দর ও অন্তর্দৃষ্টিসম্পন্ন প্রমাণগুলো লেখা আছে। একটা যুক্তি বা প্রমাণ তাঁর খুব ভালো লাগলে তিনি বলতেন: “এটা সেই বইটা থেকে নেওয়া!” (“This one’s from the book!”)। গণিতের নানা শাখার বেশ কিছু এরকম সেই বই থেকে নেওয়া প্রমাণ একত্র করে গণিতজ্ঞ মার্টিন আইগনার আর গুন্টার জিগলার লিখেছেন Proofs from THE BOOK নামে একটি আকর্ষণীয় বই। এই বইটির অনেক প্রমাণই এরদিশের আবিষ্কৃত, বাকিগুলি অন্যদের। এরকমই একটি প্রমাণ নিয়ে আলোচনা করা হয়েছে ‘বিজ্ঞান’-এর এই লেখাটিতে।


nice