সাতটা ব্রিজ, একটা পথ। ধাঁধাটার সমাধান করতে গিয়ে বেরিয়ে এলো অঙ্কের এক নতুন শাখা। সেই গল্পটা বলছে ক্লিফ স্টল, বাংলায় সাবটাইটেল বানিয়েছে ‘বিজ্ঞান’-এর স্বেচ্ছাসেবকরা।
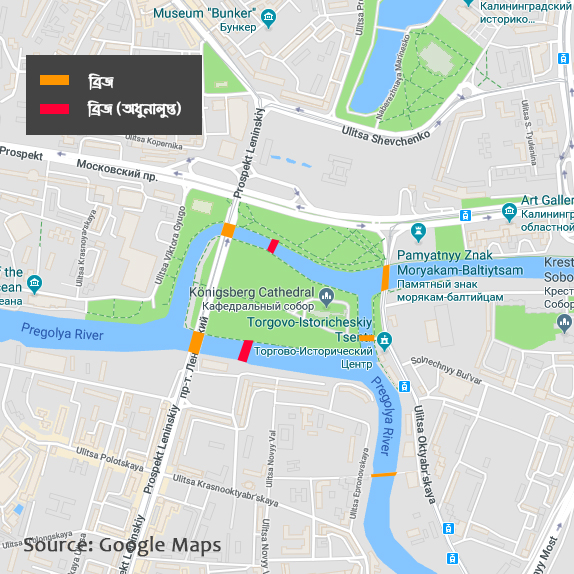
শহরের নাম কোয়েনিসবার্গ। প্রিঙ্গল নদী বয়ে যাচ্ছে শহরের মধ্যে দিয়ে। নদী এমনভাবে বইছে যে তার দুধারের ভূখণ্ড ছাড়াও মাঝে দুটো ছোট দ্বীপ সৃষ্টি করেছে। নদীর এপার ওপার করতে আছে সাত সাতটা ব্রিজ। প্রাতঃভ্রমণে বেরিয়ে ব্রিজ দিয়ে হাঁটতে হাঁটতে শহরের বাসিন্দারা একটা মজার সমস্যা তৈরী করলেন। আচ্ছা, এমন পথে কি হাঁটা সম্ভব যাতে সবকটা ব্রিজ একবার করে পার হওয়া যাবে? একবারই কিন্তু, তার বেশি করলে চলবে না।
এই সমস্যাটা সমাধান করার একটা গোদা উপায় হলো: সবকটা পথ একেক করে গুনে গুনে যাচাই করে দেখা। করতে গেলে একটু পরেই ঘাম ছুটবে আর মনে হবে, এর থেকে সোজা উপায় নিশ্চই আছে। গণিতজ্ঞ লিওনার্ড অয়লার এই উপায়টাই বার করলেন। তিনি যেটা বললেন তার সারমর্ম হলো: নদীর ধারের একেকটা ভূমিখণ্ডের উপর মনোসংযোগ করা যাক। ভূমিখণ্ডগুলোর কিছু গাণিতিক ধর্ম বার করা কি সম্ভব যেগুলো মানলে সবকটা পথ না গুনেই এই সমস্যাটার উত্তর দেওয়া যায়?
প্রথমে তিনি সমস্যাটার সহজতম সংস্করণটা তৈরী করলেন। শুধু যদি দুটো ভূমিখণ্ড থাকতো আর তাদের জুড়তো দুটো ব্রিজ, তাহলে কি হতো? এক মুহূর্তে বলে দেওয়া যায় এর উত্তর: অবশ্যই একটা পথ আছে যাতে ব্রিজগুলো একবার পেরোনো যায়। একটা ব্রিজ দিয়ে এপার থেকে ওপার, আরেকটা দিয়ে ওপার থেকে এপার। ব্যস, খেল খতম!
অয়লার যেটা করলেন, এই সহজতম সংস্করণে ভূমিখণ্ডগুলোর উপর মনোনিবেশ করলেন। লক্ষ্য করলেন যে এই সহজ কেসটাতে দুটো ভূমিখণ্ডেই জোড় সংখ্যক ব্রিজ গিয়ে প্রবেশ করছে। তারপর তিনি এই গাণিতিক ধর্মটাকে এমনভাবে বললেন যাতে আসল সমস্যাটাতেও সেটা লাগানো যায়। কিভাবে? সেটা দেখতে নিচের ভিডিওটা দেখুন1।
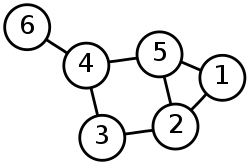 এই সমস্যাটা শুধু একটা মজার টাইমপাস নয়। এর থেকে জন্ম নিয়েছিল গণিতের একটা নতুন শাখা: গ্রাফ থিওরি। ধরুন, একরাশ বিন্দুকে জুড়ে আছে কিছু শাখা। এটা হলো একটা গ্রাফ।
এই সমস্যাটা শুধু একটা মজার টাইমপাস নয়। এর থেকে জন্ম নিয়েছিল গণিতের একটা নতুন শাখা: গ্রাফ থিওরি। ধরুন, একরাশ বিন্দুকে জুড়ে আছে কিছু শাখা। এটা হলো একটা গ্রাফ।
প্রশ্ন হলো: একেকটা বিন্দুতে কটা শাখা জুড়ে আছে, তার থেকে গোটা গ্রাফটার চরিত্র সম্বন্ধে কিছু বলা যায় কি?
গ্রাফ থিওরি ব্যবহার করা হয়েছে বহু সমস্যার সমাধানে। জীবনবিজ্ঞানের থেকে সমাজবিজ্ঞান, যেখানেই জোড়ায় জোড়ায় সংযুক্ত একদল বস্তুর প্রকৃতিনির্ণয়ের প্রয়োজন হয়েছে, গ্রাফ থিওরির উপপাদ্যগুলো সরাসরি ব্যবহার করা গেছে সেইসব সমস্যায়।
যেমন ধরুন, উপরের এক একটা বিন্দু হলো একেকটা ফেসবুক ইউসার আর শাখাগুলো বলছে কে কার ফ্রেন্ড। এখন যদি আমার এমন একটা ফ্রেন্ড থাকে যার সাথে আমার কমন ফ্রেন্ড অনেক বেশি, তার মানে হয়তো সে আমার খুব কাছের বন্ধু। সে কিছু পোস্ট করলে আমি সেটা পড়বো। ফেসবুক এইভাবে নিউজ ফিড-এ কাছের বন্ধুদের পোস্ট বেশি উপরে দেখায়, যাতে সহজেই চোখে পড়ে। এবং এই “কাছের বন্ধু”-কে চিহ্নিত করতে বন্ধুদের এই নেটওয়ার্ক-এ গ্রাফ থিওরিকে সহজেই কাজে লাগানো যায়2।
অর্থাৎ, শুধু একটা বহূদূরের সমস্যা নয়, আমাদের একদম কাছাকাছি চুপিসারে কাজ করে চলেছে ‘গ্রাফ থিওরি’। যার জন্ম অষ্টাদশ শতাব্দীতে কোয়েনিসবার্গের সাতটি ব্রিজের সমস্যার সমাধান করতে।
টীকা
- অরিজিনাল ভিডিওটি Numberphile চ্যানেল থেকে নেওয়া। বাংলায় সাবটাইটেল প্রস্তুত করেছে বিজ্ঞান-এর স্বেচ্ছাসেবক অনির্বাণ গঙ্গোপাধ্যায় ও কুণাল চক্রবর্তী।
Numberphile - গ্রাফ থিওরি আর ফেসবুক-এর যোগসাজশ নিয়ে আরো গভীরে জানতে এখানে দেখুন
Graph theory in facebook - ক্লিফ স্টল পেশায় জ্যোতির্বিদ্যার গবেষক কিন্তু তার খ্যাতি সম্পূর্ণ এক ভিন্ন ক্ষেত্রে। ১৯৮৬-তে উনি লরেন্স বার্কলে ন্যাশনাল ল্যাবরেটরি-তে কাজ করার সময় এক রুশ হ্যাকার-কে পাকড়াও করেছিলেন। ওনার এই কীর্তিটাকে ডিজিটাল ফরেনসিকস্-এর একটি শুরুর কেস হিসেবে ধরা হয়। পরবর্তীকালে উনি গণিত শিক্ষক হিসেবে খ্যাতিলাভ করেন। ওনার অসংখ্য অঙ্ক-সংক্রান্ত ইউটিউব ভিডিও এখানে পাবেন। একটা মজার গল্প হলো: আপনি যদি কাচ-এর ক্লাইন বোতল কিনতে চান, উনি তারও ব্যবস্থা করে রেখেছেন। নিজের বাড়ি থেকেই একটা কারখানা খুলেছেন। ক্লাইন বোতল হলো অঙ্কের জগতের এক অদ্ভুতুড়ে বাসিন্দা। আপনি ওই বোতলের পিঠে হাঁটতে হাঁটতে এমন পথ নিতে পারেন যাতে শুরুর বিন্দুতে ফিরে এলে আপনি শুরুর অবস্থার তুলনায় একেবারে উল্টে যাবেন।

Good