আমাদের এই আলোচনাটা রোধ()-এর বদলে রোধাঙ্ক(
) নিয়ে করা বেশি সুবিধাজনক, কারণ কোনো এক টুকরো পরিবাহীর রোধ তার উপাদান ছাড়াও দৈর্ঘ্য(
) আর প্রস্থচ্ছেদ(
)-এর ওপর নির্ভর করে। এই নির্ভরতাটা ঠিক এইরকম:
, যেখানে
হলো টুকরোটার উপাদানের রোধাঙ্ক। এছাড়া আলোচনার সুবিধের জন্য আমরা এখানে শুধু ধাতব পরিবাহীর (যেমন লোহা বা তামা বা সোনা) কথা ভাববো। সুতরাং প্রশ্নটা এখন দাঁড়ালো কেন বিভিন্ন ধাতুর রোধাঙ্ক আলাদা হয় ?
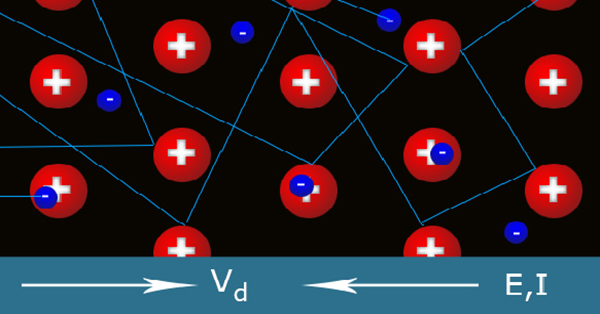
রোধ কেন ধাতুবিশেষে আলাদা সেটা বুঝতে হলে, ইলেক্ট্রন-এর প্রবাহে কিসে বাধা পড়ে সেটা আগে বুঝতে হবে। আমরা জানি যে তড়িৎপ্রবাহ বা ইলেকট্রিক কারেন্ট হচ্ছে ইলেক্ট্রন-এর একমুখী প্রবাহ, সেই প্রবাহে বাধা পড়লে রোধ সৃষ্টি হয়। তাই, রোধ কেন ধাতুবিশেষে আলাদা সেটা বুঝতে হলে, ইলেক্ট্রন-এর প্রবাহে কিসে বাধা পড়ে সেটা আগে বুঝতে হবে।
রোধ কেন ধাতুবিশেষে আলাদা সেটা বুঝতে হলে, ইলেক্ট্রন-এর প্রবাহে কিসে বাধা পড়ে সেটা আগে বুঝতে হবে।
ধাতুর পরমাণুর একদম বাইরের শক্তিস্তরের ইলেক্ট্রনগুলো খুব আলগাভাবে আবদ্ধ থাকে। তাই যখন অনেক পরমাণু একসাথে জড়ো হয়ে এক টুকরো কঠিন ধাতু তৈরী করে তখন এই বাইরের ইলেক্ট্রনগুলো আর পরমাণুদের মধ্যে আটকা পড়ে থাকে না। তারা এই কঠিন পদার্থের সর্বত্র চলে বেড়াতে পারে। এদের বলা হয় মুক্ত ইলেক্ট্রন: এদের চলাচলেই কারেন্ট সৃষ্টি হয়। যদি প্রতিটি পরমাণু থেকে সংখ্যক মুক্ত ইলেক্ট্রন বেরোয় আর পরমাণুর সংখ্যা-ঘনত্ব (প্রতি ঘনসেন্টিমিটারে কতগুলো পরমাণু আছে) হয়
, তাহলে ধাতুটার মুক্ত ইলেক্ট্রনের সংখ্যা-ঘনত্ব হবে
।
ইলেক্ট্রনগুলো এতো ছোট যে তাদের চলাফেরা বুঝতে কোয়ান্টাম মেকানিক্স লাগে। এরম মাথা গোলানো অবস্থায় পদার্থবিদরা একটা চালাকি হামেশাই করে থাকে। তারা বলে যে এই সিস্টেমটার খুব সরল একটা থিওরি বানানো যাক, যাকে বলে “টয় মডেল”। এখন এই চলাচল কিভাবে হয় ভাবতে বসলে একটু পরেই মাথা গুলিয়ে যাবে। কারণ একটুকরো ধাতু একটা খুব জটিল সিস্টেম। তার মধ্যে একগাদা মুক্ত ইলেক্ট্রন আছে আর থাকে থাকে সাজানো পরমাণু আছে (যেগুলো ইলেক্ট্রন বেরিয়ে যাওয়ার ফলে ধনাত্মক আয়নে পরিবর্তিত হয়েছে)। এরা সবাই আধানযুক্ত কণা, তাই এদের পরস্পরের মধ্যে কুলম্বের সূত্র অনুযায়ী স্থির তড়িৎ বল-ও কাজ করছে। তার ওপর ইলেক্ট্রনগুলো এতো ছোট যে তাদের চলাফেরা বুঝতে কোয়ান্টাম মেকানিক্স লাগে। এরম মাথা গোলানো অবস্থায় পদার্থবিদরা একটা চালাকি হামেশাই করে থাকে। তারা বলে যে এই সিস্টেমটার খুব সরল একটা থিওরি বানানো যাক, যাকে বলে “টয় মডেল”। সেটা হয়তো খুব সঠিক হবে না, সিস্টেমের সব জটিলতা কে ধরবেও না, কিন্তু সেটা নিয়ে ভাবনাচিন্তা অন্তত করা যাবে। আর মডেলটা থেকে অন্তত কিছুটা আইডিয়া পাওয়া যাবে আসল সিস্টেমটায় কি ঘটছে। এটা করা গেলে তারপর একটু একটু করে মডেলটাকে আরও সঠিক করার চেষ্টা করা হয়।
ইলেক্ট্রনগুলো এতো ছোট যে তাদের চলাফেরা বুঝতে কোয়ান্টাম মেকানিক্স লাগে। এরম মাথা গোলানো অবস্থায় পদার্থবিদরা একটা চালাকি হামেশাই করে থাকে। তারা বলে যে এই সিস্টেমটার খুব সরল একটা থিওরি বানানো যাক, যাকে বলে “টয় মডেল”।
প্রথমে ভাবা যাক বাইরে থেকে কোনো বল প্রযুক্ত না হলে ধাতুর মধ্যে মুক্ত ইলেক্ট্রনদের চলাফেরার সবথেকে সরল মডেল কি হতে পারে। ধরা যাক একটা মুক্ত ইলেক্ট্রন নিউটনের প্রথম গতিসূত্র অনুযায়ী সরলরেখায় সমবেগে চলে, যতক্ষণ না কোনো একটা আয়নে ধাক্কা খাচ্ছে। ধাক্কা খাওয়ায় তার বেগের মান ও দিক দুইয়েরই পরিবর্তন ঘটে: এরপর সে নতুন বেগে আবার চলতে শুরু করে যতক্ষণ না আরেকটা আয়নে ঠোক্কর মারছে। ধাক্কা খাওয়ার পর ইলেক্ট্রনটার যে কোনো দিকে যে কোনো গতিতে চলার সম্ভাবনা সমান এবং ধাক্কার আগের বেগের সাথে তার কোনো সম্পর্ক নেই।
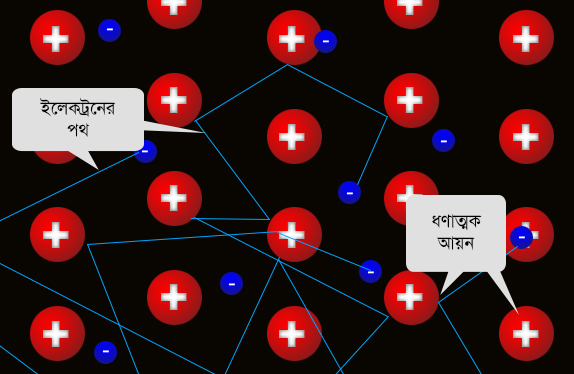
এখন যদি একটা ইলেক্ট্রনের গতিপথ অনেকক্ষণ ধরে অনুসরণ কর তাহলে দেখবে সেটা অনেক সরলরেখাংশ দিয়ে তৈরী একটা আঁকাবাঁকা পথে চলেছে ধাক্কা খেতে খেতে (উপরের ছবিটা দেখো)। পরপর দুটো ধাক্কার মধ্যে সময়কে যদি বলি তাহলে গোটা পথ বরাবর এরকম অনেকগুলো
পাওয়া যাবে:
। এদের গড়কে আমরা নাম দেব
, যেখানে
কে বলা হয় ওই ধাতুতে ইলেক্ট্রনের রিলাক্সেশন টাইম। (2 গুণিতক টা নিয়ে বেশি মাথা ঘামিয়ো না, জাস্ট অংকের একটু সুবিধার জন্য ওটা ঢোকানো হয়…যেটা আমরা একটু পরেই দেখতে পাবো।)
শেষে ধরা যাক এই ইলেক্ট্রনগুলো পুরোপুরি সনাতনী বস্তুকণার মতো আচরণ করে। অর্থাৎ বাইরে থেকে কোন বল প্রয়োগ করলে তার ফলে (নিউটনের দ্বিতীয় গতিসূত্র অনুসারে) ইলেক্ট্রনের ত্বরণ হয়
.
ব্যাস, আমাদের টয় মডেল রেডি! মডেল এর অনুমানগুলো থেকে আপাততঃ মনে হচ্ছে আয়নের সাথে ধাক্কা-ই ইলেক্ট্রনের চলায় বাধা দেয় আর রোধের সৃষ্টি করে। রিলাক্সেশন টাইম যত কম হবে, ধাক্কাও তত বেশি লাগবে আর রোধ-ও বাড়বে। বিভিন্ন ধাতুতে আয়নগুলোর সজ্জা আলাদা আলাদা রকমের, মুক্ত ইলেক্ট্রন আর আয়নের আকর্ষণের মাত্রাও আলাদা। এইসব কারণে রিলাক্সেশন টাইম এর মান, আর সেই সূত্রে রোধাঙ্ক-ও, ধাতুবিশেষে আলাদা হওয়ার কথা।
আর কোনো কারণে কি রোধাঙ্কের মান আলাদা হতে পারে? এই প্রশ্নের একটা সম্পূর্ণ উত্তর পেতে হলে আমাদের টয় মডেলে রোধাঙ্কের মান ঠিক কত সেটা অঙ্ক কষে বার করতে হবে। মডেলটা কতটা সঠিক সেটা বোঝার জন্য-ও অঙ্কটা কষা প্রয়োজন। কারণ যদি এর থেকে বার করা রোধাঙ্কের মান এক্সপেরিমেন্ট-এ পাওয়া মান-এর থেকে আলাদা হয়, তাহলে বোঝা যাবে টয় মডেল-এ আরো মালমশলা লাগবে। সেটা করার চেষ্টা করা যাক।
আমরা প্রথমে এক টুকরো ধাতুর (যার দৈর্ঘ্য আর প্রস্থচ্ছেদ
) রোধ নির্ণয় করবো। তারপর সেখান থেকে রোধাঙ্ক বার করা কঠিন হবে না। আমরা জানি রোধের সংজ্ঞা হলো
. সুতরাং টুকরোটার দুই প্রান্তের বিভব-প্রভেদ
হলে তার মধ্যে তড়িৎপ্রবাহ
কত হবে সেটা আমাদের জানা দরকার। তাহলেই কেল্লা ফতে।
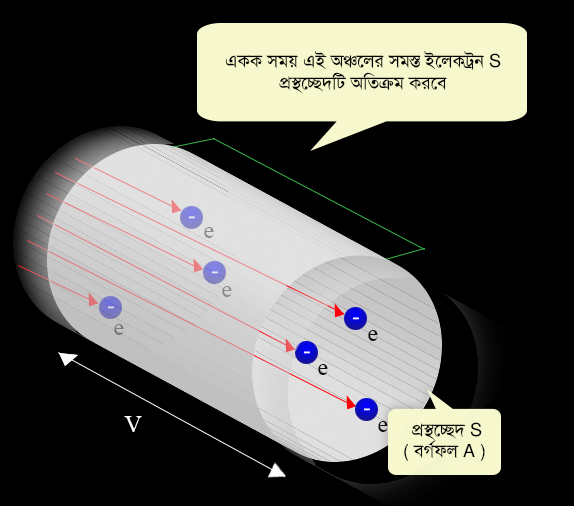
ধাতুটার মধ্যে ইলেক্ট্রনের গড় বেগ যদি হয় (অর্থাৎ একক সময়ে কোনো একটা ইলেক্ট্রন গড়ে
দূরত্ব যায়) তাহলে নিচের ছবিটা থেকে দেখা যাচ্ছে যে একক সময়ে
ঘনফলে যত ইলেক্ট্রন আছে সবাই S প্রস্থচ্ছেদটি অতিক্রম করবে। যেহেতু ইলেক্ট্রনের সংখ্যা-ঘনত্ব
, এতে যতটা আধান প্রবাহিত হবে তা হলো
, যেখানে ইলেক্ট্রনের আধান হলো
(যা একটা ধ্রুবক)। একক সময়ে যতটা আধান প্রবাহিত হয় তাকেই তড়িৎ-প্রবাহ বলে। সুতরাং
।
আমাদের টয় মডেলে এই বেগ -এর দুটো অংশ আছে। প্রথমটার কারণ হলো আয়ন এর সাথে ধাক্কা। আগেই বলেছি ধাক্কা খাওয়ার পর ইলেক্ট্রনটার যে কোনো দিকে যে কোনো গতিতে চলার সম্ভাবনা সমান: অর্থাৎ এই অংশটার গড় মান শূন্য। তাই আমাদের বাকি আলোচনায় আমরা এই অংশটার কথা বেমালুম চেপে যাবো।
দ্বিতীয় অংশটা আসে ইলেক্ট্রনের ওপর তাড়িতীক বলের জন্য। এর গড় মান কত সেটা বার করা যাক। টুকরোটার দুই প্রান্তের মধ্যে বিভব-প্রভেদ প্রয়োগ করলে তার মধ্যে তড়িৎ-ক্ষেত্র হয়
. এই তড়িৎ-ক্ষেত্র একটা মুক্ত ইলেক্ট্রনের ওপর
বল প্রয়োগ করবে। এর ফলে (নিউটনের দ্বিতীয় গতিসূত্র অনুসারে) ইলেক্ট্রনের ত্বরণ হবে
, যেখানে m হলো ইলেক্ট্রনের ভর।
পরপর দুটো ধাক্কার মধ্যেকার পথটুকুতে এই ত্বরণের ফল কি হচ্ছে দেখা যাক। ছবিতে দেখা যাচ্ছে ইলেক্ট্রনটা প্রথমে A আয়নে ধাক্কা খেলো, তারপর AB পথ বরাবর চলতে চলতে শেষে B-তে গিয়ে লাগলো। সুতরাং AB পথের শুরুতে ইলেক্ট্রনের গতি (কারণ ধাক্কার পর সে সবে চলা শুরু করেছে) আর শেষে
. তাহলে গড় বেগ হলো
এর থেকে আমরা পাই
এর থেকে আসে রোধ
এবং রোধাঙ্ক
আমরা শুরুতে রিলাক্সেশন টাইমের ওপর রোধাঙ্কের যে নির্ভরতার কথা ভেবেছিলাম তা এই ফর্মুলার সাথে মিলছে: রিলাক্সেশন টাইম বাড়লে রোধাঙ্ক কমে। কিন্তু এই ফর্মুলা বলছে আরও দুটো জিনিসের জন্য রোধাঙ্কের মান ধাতুবিশেষে আলাদা হতে পারে:
- ইলেক্ট্রনের ভর (
): প্রথমে মনে হবে ইলেক্ট্রনের ভর তো একটা ধ্রুবক। তার মান আবার বিভিন্ন ধাতুতে আলাদা হবে কি করে? কিন্তু আমাদের টয় মডেলে আমরা একটা জিনিস ধরিনি: ইলেক্ট্রনটা যখন সরলরেখায় চলে তখনো তার ওপর চারিপাশের আয়নগুলোর আকর্ষণ কাজ করে। এই আকর্ষণের ফলে ধাতুর মধ্যে মুক্ত ইলেক্ট্রনের আপাত-ভর
শূন্যস্থানে ইলেক্ট্রনের ভরের থেকে আলাদা হয়ে যায়।1 বিভিন্ন ধাতুতে আয়নগুলোর সজ্জা আলাদা আলাদা রকমের, ইলেক্ট্রন আর আয়নের আকর্ষণের মাত্রাও আলাদা। তাই
-এর মান-ও আলাদা হওয়ার কথা।
যত বেশি হবে, ইলেক্ট্রনকে নড়ানো তত কঠিন হবে আর রোধাঙ্ক-ও বাড়বে।
- ইলেক্ট্রনের সংখ্যা-ঘনত্ব (
): এটা বোঝা বেশ সোজা। ধাতুতে বেশি মুক্ত ইলেক্ট্রন থাকলে পরিবাহিতা বাড়ে, অর্থাৎ রোধাঙ্ক কমে।
ধাতুদের পরিবাহিতা মেপে দেখা যায় যে আমাদের এই টয় মডেল আদতে খুব একটা খারাপ না। স্বাভাবিক তাপমাত্রায় অনেক পরিচিত ধাতুর রোধাঙ্ক-ই উপরের ফর্মুলা মেনে চলে। অবশ্য ইলেক্ট্রনের আপাত ভর আর রিলাক্সেশন টাইমের মান বার করতে কোয়ান্টাম মেকানিক্স প্রয়োগ করতে হয়: যে বিষয়টা আমরা এখানে আলোচনা করিনি। আর এই মডেল অনেক ক্ষেত্রে খাটলেও পদার্থের মধ্যে ইলেকট্রনের চলার আরও নিঁখুত হিসেব করতে কোয়ান্টাম মেকানিক্স অবশ্য প্রয়োজন। কিন্তু ধাতব পদার্থের এইসব হাজার জটিলতা স্বত্বেও কেন আমাদের এই ছোট্ট মডেল-টা আদৌ সফল হলো সেটা পদার্থবিদ-দের কাছে একটা বিশাল ধাঁধা ছিল অনেক বছর। তার গল্প ভবিষ্যতে কোনো লেখায় বলার ইচ্ছে রইলো।
টীকা