গোড়ার কথা
গত শতাব্দীর শুরুর দিকে পদার্থবিদ্যায় দুটি নতুন ধারার সূত্রপাত হয়। একটি বিশেষ আপেক্ষিকতাবাদ বা স্পেশাল রিলেটিভিটি (special relativity) এবং অন্যটি কোয়ান্টাম বলবিদ্যা (quantum mechanics)। প্রথমটি আসে ১৯০৫ সালে আইনস্টাইনের হাত ধরে। আলোর গতিবেগের কাছাকাছি গতিতে ধাবমান যে কোনো বস্তুর ধর্মকে বিশেষ আপেক্ষিকতাবাদের সাহায্যে ব্যাখ্যা করা যায় [১]। অন্য ধারাটি প্রায় সমসাময়িকভাবে আসে বেশ কয়েকজন পদার্থবিদের কাজের মাধ্যমে; প্লাঙ্ক, আইনস্টাইন, ডি ব্রয়লি ও স্রোয়েডিঙ্গার তাঁদের মধ্যে অন্যতম। অতিক্ষুদ্র কণা, যেমন অণুর থেকেও ছোট ইলেক্ট্রনকে ব্যাখ্যা করতে হলে কোয়ান্টাম বলবিদ্যার প্রয়োজন। কিন্তু, সেই ইলেক্ট্রনের গতিবেগ আলোর গতিবেগের থেকে অনেক কম হলে তবেই এই তত্ত্ব দিয়ে তাদের ধর্মকে ব্যাখ্যা করা সম্ভব। অতএব দুটি আলাদা জগতের ধর্ম ব্যাখ্যা করার জন্য দুটি আলাদা তত্ত্ব বা থিওরি (theory) তৈরী হয়। এদের চরিত্র অনেকটাই আলাদা। ফলত এই দুটি থিওরি-র মেলবন্ধন ঘটিয়ে আলোর গতিবেগের কাছাকাছি গতিতে ধাবমান একটি ইলেক্ট্রনের গতিপ্রকৃতি নির্ণয় করা মোটেই সোজা ছিল না [২]।
আলোর গতিবেগের কাছাকাছি গতিবেগসম্পন্ন ইলেক্ট্রনের ধর্ম বোঝার জন্য প্রয়োজন পড়ে “ডিরাক সমীকরণ”-এর।
১৯২৭ সালে এই সমস্যাটিই ভাবাচ্ছিল ব্রিটিশ পদার্থবিদ পল এড্রিয়ান মরিস ডিরাক-কে। তাঁর চিন্তাভাবনা থেকে অবশেষে এই সমস্যাটির একটি সমাধান বের হয়। ডিরাক দেখান যে আলোর গতিবেগের কাছাকাছি গতিবেগসম্পন্ন ইলেক্ট্রন-দের ধর্ম বোঝাতে গেলে প্রয়োজন একটি নতুন সমীকরণের যাকে আমরা এখন ডিরাক সমীকরণ নামে জানি।

অতএব ডিরাক সমীকরণের মাধমে কোয়ান্টাম বলবিদ্যা আর বিশেষ আপেক্ষিকতাবাদের সমন্বয় ঘটে। কিন্তু এই ডিরাক সমীকরণটির এমন কিছু অদ্ভুত সমাধান ছিল, যা সাধারণ কোয়ান্টাম বলবিদ্যার স্রোয়েডিঙ্গারের সমীকরণে ছিল না। যেমন, এই সমীকরণ থেকে জানা যায় যে ঋণাত্মক আধানসম্পন্ন ইলেক্ট্রনের এক জাতভাই আছে – পজিট্রন- যার ভর ইলেক্ট্রনের সমান কিন্তু আধান ধনাত্মক। এধরণের কণা থাকার সম্ভাবনা ডিরাক-এর সমীকরণের একটি বড় সাফল্য। ১৯৩২ সালে কার্ল ডেভিড অ্যান্ডার্সন এই কণাটিকে ক্লাউড চেম্বারে শনাক্ত করেন। কিন্তু, শেষমেশ ডিরাক-এর সমীকরণ যথেষ্ট ছিল না। আলোর গতিবেগের কাছাকাছি ইলেক্ট্রনদের বুঝতে হলে একই তত্ত্বের আওতায় আলোককণা ও তার সাথে ইলেক্ট্রনের পারস্পরিক ক্রিয়া-প্রতিক্রিয়াকে ধরা প্রয়োজন। এই কাজটি করতে গিয়ে জন্ম হয় কোয়ান্টাম ইলেক্ট্রোডাইনামিক্স (quantum electrodynamics)-এর, যাকে পদার্থবিদ্যার জগতে অন্যতম সফল একটি থিওরি বলা চলে [৩]। এর ফলে ডিরাক-এর সমীকরণ ও তার সমাধানের বিচিত্র ধর্ম আর পরীক্ষামূলকভাবে যাচাই করা হয় না।
বিশ বছর পর
ডিরাক-এর সমীকরণটি আবিষ্কারের প্রায় কুড়ি বছর পর এক কানাডিয়ান পদার্থবিদ ফিলিপ রাসেল ওয়ালেস গ্রাফাইট নিয়ে গবেষণা করছিলেন। গ্রাফাইট-এর সাথে আমরা সবচেয়ে ভালোভাবে পরিচিত পেন্সিল-এর সীসের মাধ্যমে। ছোটবেলায় কেমিস্ট্রি বইয়ে বহুরূপী মৌল কার্বন-এর সবচেয়ে পরিচিত রূপভেদ হিসেবে গ্রাফাইট-এর কথাই আমরা শিখেছি।
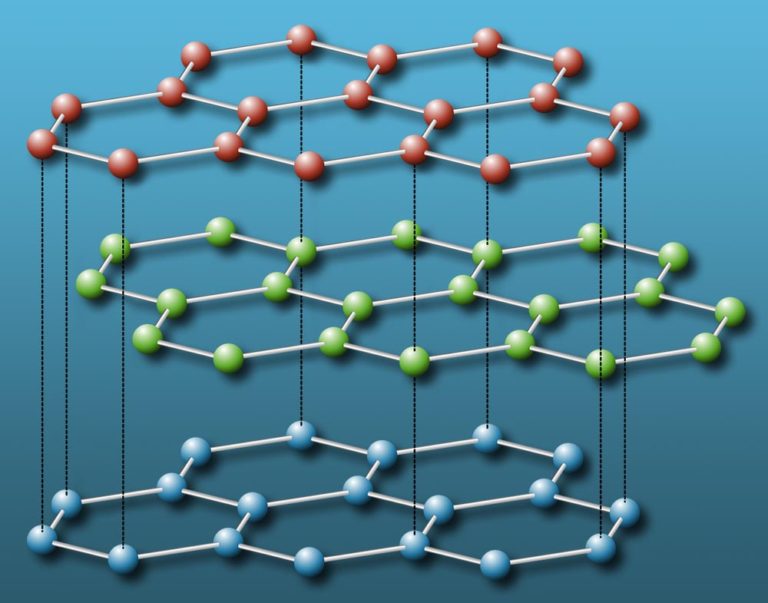
গ্রাফাইট-এর গঠন অনেকটা এইরকম। ভাবা যাক যে স্তরে স্তরে একের পিঠে আরেকটি সমতল বসানো। একেকটি তলায় খাপে খাপ মিলিয়ে রয়েছে ষড়ভুজ বা হেক্সাগন (hexagon) আর সেই ষড়ভুজের কোণাগুলিতে রাখা রয়েছে কার্বন অণুদের। একই তলায় যে কার্বন অণুগুলি রয়েছে, তাদের মধ্যে রাসায়নিক বন্ধন খুবই দৃঢ়। কিন্তু, প্রতিবেশী সমতলগুলির কার্বন অণুদের মধ্যে সেই বন্ধন নেই বললেই চলে।
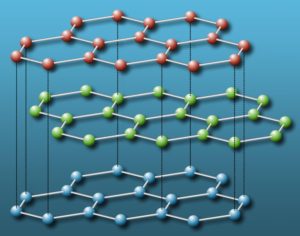
ওয়ালেস যখন তাত্ত্বিকভাবে গ্রাফাইট নিয়ে গবেষণা করছেন, তদ্দিনে তার উপর পরীক্ষামূলক গবেষণা অনেকদূর এগিয়েছে। যেমন, ভারতীয় পদার্থবিদ কে. এস. কৃষ্ণান গ্রাফাইটের উপর বেশ কিছু গুরুত্বপূর্ণ কাজ করে ফেলেছেন। জানা গিয়েছে, গ্রাফাইট-এর মধ্যে তাপ বা বিদ্যুৎ পরিবাহিতা সব দিকে সমান নয় [৪]।
এই পরিস্থিতিতে, তাত্ত্বিকভাবে গ্রাফাইট-এর মধ্যে ইলেক্ট্রন চলাচলের উপর গবেষণা করছিলেন ওয়ালেস। ‘টাইট বাইন্ডিং মডেল’ (tight-binding model) নামে এক পদ্ধতির সাহায্যে। পদ্ধতিটিতে একটি ‘ল্যাটিস’ (lattice) থেকে শুরু করা হয়। ল্যাটিস হলো শূন্যে নিয়মিত দূরত্বে সাজানো বিন্দু। যেমন, নিচে একটি দ্বিমাত্রিক ল্যাটিসের ছবি দেওয়া হলো:

একটি চলন্ত ইলেক্ট্রনের অবস্থান যদি এই ল্যাটিসের বিন্দুগুলির মধ্যেই সীমিত থাকে, তাহলে তার গতিশক্তিকে এমনভাবে লেখা যাবে যেন সে একটি বিন্দু থেকে আরেকটি বিন্দুতে লাফাচ্ছে। একটি বিন্দু ধ্বংস হওয়ার সাথে সাথে তার প্রতিবেশী বিন্দু সৃষ্টি হচ্ছে। সংক্ষেপে এটিই ‘টাইট বাইন্ডিং মডেল’। এই মডেলটি কিভাবে তৈরী হয়, সেই অঙ্কের বিশদ বর্ণনায় গেলাম না, কিন্তু এটি যে কোনো ল্যাটিস-এর ক্ষেত্রেই প্রযোজ্য। গ্রাফাইট-এর এক একটি সমতলে যে ষড়ভুজাকার ল্যাটিস রয়েছে, ওয়ালেস এই মডেলটি তার উপর বসিয়ে অঙ্ক কষলেন। তিনি দেখালেন যে গ্রাফাইট-এর সমতলগুলির মধ্যে যে যৎসামান্য বন্ধন রয়েছে, তাকে যদি উপেক্ষা করা যায়, তাহলে এক একটি তলার ইলেক্ট্রনগুলি ডিরাক সমীকরণ মেনে চলে। হ্যাঁ, ঠিক সেই ডিরাক সমীকরণ যেটি আবিষ্কার হয়েছিল আলোর গতিবেগের কাছাকাছি বেগে ছুটন্ত মুক্ত, বন্ধনহীন ইলেক্ট্রন-এর জন্য! ওয়ালেসের কাজ দেখায় যে একই সমীকরণ খাটে গ্রাফাইটের একটি তলায় ষড়ভুজাকার ল্যাটিস-এ আবদ্ধ ইলেক্ট্রনদের জন্যেও! যদিও ইলেক্ট্রনগুলির গতিবেগ আলোর গতিবেগের মাত্র ১/১০০ ভগ্নাংশ মতো।
ওয়ালেস দেখালেন যে গ্রাফাইটের সমতলগুলির মধ্যে থাকা যৎসামান্য বন্ধন যদি উপেক্ষা যায়, তাহলে প্রতিটি তলের ইলেক্ট্রন “ডিরাক সমীকরণ” মেনে চলে।
কিন্তু, এতদিন অব্দি এই পুরো ব্যাপারটাই তাত্ত্বিক স্তরে ছিল। গ্রাফাইটে তো স্তরে স্তরে সমতলগুলি বসানো রয়েছে, তার মধ্যে থেকে একটি স্তর-কে আলাদা করবে কে? মনে রাখতে হবে, ডিরাক সমীকরণ পেতে গেলে স্তরগুলির মধ্যে বন্ধনকে শূন্য হতে হবে; ওয়ালেস দেখালেন যে বন্ধনগুলিকে বাদ না দিলে ডিরাক সমীকরণ পাওয়া অসম্ভব। তাই, একটি স্তর-কে আলাদা করতে না পারলে পরীক্ষামূলকভাবে ওয়ালেস-এর আবিষ্কার যাচাই করা সম্ভব নয়। অতএব, পদার্থবিদদের মধ্যে যাঁরা বস্তুর ভিতর ইলেক্ট্রন চলাচল নিয়ে মাথা ঘামান, তাঁরা এই ডিরাক সমীকরণের পুনরাবির্ভাবকে পাত্তা দিলেন না।
একবিংশ শতাব্দীর শুরুতে
ম্যানচেস্টার, ইংল্যান্ড, ২০০৪। আন্দ্রে গাইম আর কনস্টান্টিন নোভোসেলভ এই তাত্ত্বিক কল্পনাকে বাস্তবে রূপান্তরিত করলেন। গ্রাফাইট-এর উপর স্কচ টেপ (আমরা যাকে সেলোটেপ বলি) দিয়ে ঘষলে যে পাতলা গ্রাফাইট-এর আঁশগুলো বেরোয়, তার মধ্যে থেকে একটি মাত্র স্তরকে আলাদা করতে সক্ষম হলেন তারা। একটি স্তর, যার উপর ষড়ভুজাকার ল্যাটিস-এর কোনায় কোনায় বসে আছে কার্বন অণু। একেই আমরা ‘গ্রাফিন’ নামে জানি।

তাঁদের যুগান্তকারী গবেষণাপত্রটি ২০০৪-এ ‘সায়েন্স’ পত্রিকতে বেরোলো [৫]। এই গবেষণাটি এবং তার পরবর্তী কয়েকটি কাজের ফলে দেখা গেল যে গ্রাফিন-এর মধ্যে ইলেক্ট্রন চলাচল সাধারণ ধাতুর থেকে একদম আলাদা। এবং এই ইলেক্ট্রন চলাচলকে বুঝতে হলে ডিরাক সমীকরণের সাহায্য নিতেই হবে। এর ফলে তাত্ত্বিক এবং পরীক্ষামূলক ঘন বস্তুর পদার্থবিদ্যা বা কনডেন্সড ম্যাটার ফিজিক্স (condensed matter physics), দুটি ধারাতেই একটি নতুন জগৎ খুলে গেল। ডিরাক সমীকরণ যে সূত্রে প্রথম এসেছিলো, সেই কণাপদার্থবিদ্যার জগতে তাকে পরীক্ষামূলকভাবে যাচাই করা যায়নি। কারণ কণাপদার্থবিদ্যার যে কোনো পরীক্ষায় একসাথে আলোককণা এবং ইলেক্ট্রন, দুটিই ধর্তব্যের মধ্যে এসে যায়। ‘গ্রাফিন’-এ ইলেক্ট্রনের গতিবেগ আলোর গতিবেগের তুলনায় অনেক কম হওয়াতে সেই সমস্যাটি নেই।
দ্বিতীয়ত, ‘গ্রাফিন’ (বা যে কোনো ঘন বস্তুর ভিতর) ইলেক্ট্রন-রা একে অপরকে প্রভাবিত করে। ডিরাক নিজের সমীকরণটি লিখেছিলেন এমন ইলেক্ট্রনের জন্য যে শূন্যে আলোর গতিবেগের কাছাকাছি গতিবেগে ছুটছে। অন্যান্য ইলেক্ট্রনদের দ্বারা প্রভাবিত হলে ‘ডিরাক সমীকরণ’-এর ‘মুক্ত’ ইলেক্ট্রন-দের কি পরিবর্তন হবে, সেটি সম্পূর্ণ নতুন গবেষণার বিষয়।
গ্রাফিন “ডিরাক সমীকরণ”-এর ওপর পরীক্ষামূলক গবেষণায় একটা যুগান্তর এনেছে।
তবে গ্রাফিন-এর সবচেয়ে গুরুত্ত্বপূর্ণ দিক হলো এই যে, ‘গ্রাফিন’ আসার ফলে সহজে ডিরাক সমীকরণের ভবিষ্যদ্বাণী নিয়ে পরীক্ষামূলক গবেষণা করার একটি উপায় পাওয়া গিয়েছে । এইসব পরীক্ষার জন্য বিশালাকায় যন্ত্রপাতির প্রয়োজন নেই, সাধারণ বিশ্ববিদ্যালয়ের গবেষণাগারের টেবিল আর যন্ত্রপাতিই যথেষ্ট।
বিচিত্র এই ডিরাক সমীকরণ
কিন্তু, এই সমীকরণটি বাস্তবে প্রতিফলিত হলে সেটি আশ্চর্যের ব্যাপার হবে কেন? কারণ, এর সমাধানের এমন কিছু বৈশিষ্ট্য আছে যা পোড়খাওয়া কোয়ান্টাম বলবিদ্যার গবেষককেও তাজ্জব বানিয়ে দেয়। তার মধ্যে একটির কথা বলি।
ডিরাক তার সমীকরণটি লেখার বছর দুই পর সুইডিশ পদার্থবিদ অস্কার ক্লাইন একটি অদ্ভুত জিনিস লক্ষ্য করেন। সমীকরণটি মেনে চলে যেসব ইলেক্ট্রন (সংক্ষেপে, ‘ডিরাক ইলেক্ট্রন’), তাদের পথে যদি একটি বাধা তৈরী করা হয়, তারা বেশ অস্বাভাবিকভাবে আচরণ করে।
এখন, স্বাভাবিক-টি কি, সেটিও একটু ব্যাখ্যা করা প্রয়োজন। ক্লাসিকাল বা রোজকার পরিচিত জগতে, একটি দেয়ালের দিকে বল ছুঁড়ে দিলে কি হবে, সেটি বলতে খুব বেশি কসরত করতে হয়না। বলটি দেয়ালের উচ্চতার থেকে নিচে হলে ধাক্কা খেয়ে ফিরে আসবে, আর উচ্চতার উপরে হলে বেরিয়ে যাবে। কোয়ান্টাম জগতে কিন্তু সেরকমটি হয়না। কোয়ান্টাম জগতে ধীরগতির ইলেক্ট্রনদের ‘স্রোয়েডিঙ্গার সমীকরণ’ (Schroedinger’s equation)-এর মাধ্যমে বোঝানো হয়। একটি বাধার উপস্থিতিতে স্রোয়েডিঙ্গার সমীকরণের সমাধান করলে দেখা যায় যে ইলেক্ট্রন-এর গতিশক্তি যাই হোক, বাধার অপরদিকে ইলেক্ট্রন-টিকে পাওয়ার একটা সম্ভাবনা থেকেই যায় (নিচের ছবিটিতে দেখ)। ইলেক্ট্রন-এর গতিশক্তি খুব কম হলে সম্ভাবনাটি খুবই ক্ষীণ, কিন্তু ক্লাসিকাল জগতের বলটির মতো একেবারে শূন্য নয়। একে বলে ‘টানেলিং’ বা সুরঙ্গিকরণ এবং এটি একমাত্র কোয়ান্টাম জগতেই সম্ভব।
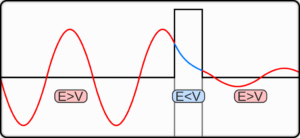
খুব অদ্ভুত শোনালেও এই প্রকৃতিটি সম্বন্ধে একটা চেনা ছবি তৈরী করা যায়। একটি ইলেক্ট্রন-এর গতিশক্তি যদি বাধা টপকানোর শক্তির তুলনায় খুব কম হয়, এবং অনেকগুলি এরকম ইলেক্ট্রনকে একটি বাধার দিকে চালিত করা যায়, তাহলে বেশিরভাগ ইলেক্ট্রনগুলিই আটকে যাবে। খুব কম সংখ্যক ইলেক্ট্রনদেরই বাধার উল্টোদিকে পাওয়া যেতে পারে। আর গতিশক্তি যদি দেয়াল পেরোনোর শক্তির তুলনীয় হয়, তাহলে অনেক বেশি ইলেক্ট্রনকে বাধার উল্টোদিকে পাওয়া যাবে। এক কথায়, ইলেক্ট্রন-এর গতিশক্তি বাড়ালে বাধা পার হবার সম্ভাবনা বাড়তে থাকে।
পরিচিত জগতের থেকে অন্যরকম হলেও কোয়ান্টাম জগতের সাথে অভ্যস্ত হতে হতে তাত্ত্বিক পদার্থবিদদের মনে এই ছবিটি গেঁথে যায়। ডিরাক ইলেক্ট্রন-রা এই ছবিটির মূলে আঘাত করে। অস্কার ক্লাইন দেখালেন যে বাধাটি যথেষ্ট পাতলা হলে সব ইলেক্ট্রন-ই সেটি পেরোতে পারে ! সে বাধার উচ্চতা যাই হোক না কেন, ইলেক্ট্রন-টি সোজাসুজি বাধায় এসে পড়লে সে শতকরা একশোভাগ নিশ্চয়তার সাথে বাধাটি পেরিয়ে যাবে। যেন বাধাটি নেই বললেই চলে ! এটি শুধু আমরা দেয়ালে বল ছুঁড়লে যা দেখি, তার থেকে আলাদা নয়, একেবারে উল্টো! একেই ‘ক্লাইন প্যারাডক্স’ বলা হয়ে থাকে।
ডিরাক ইলেক্ট্রন-এর এই অদ্ভুত প্রকৃতি পরীক্ষামূলকভাবে আগে যাচাই করা সম্ভব হয়নি। ‘গ্রাফিন’-এর সাহায্যে গবেষণাগারের টেবিল-এর উপরই এটি করা সম্ভব। এবং প্রাথমিকভাবে ইঙ্গিত পাওয়া যাচ্ছে যে এই বাধাহীন চলাচলটি সত্যিই হতে পারে, যদিও নিশ্চিতভাবে এটা প্রমান করতে এখনো অনেক এক্সপেরিমেন্ট-এর প্রয়োজন [৬]।
তাহলে কি দাঁড়ালো
বলা যায়, ঘনবস্তুর জগতে ‘গ্রাফিন’ প্রথম উদাহরণ যেখানে সম্পূর্ণ আলাদা প্রসঙ্গে বহুকাল আগে লেখা একটি সমীকরণকে কণা পদার্থবিদ্যার জগৎ থেকে বার করে এনে একটি টেবিলের উপর পরীক্ষা করে যাচাই করা সম্ভব হচ্ছে।
আর ঘনবস্তুর পদার্থবিদ্যার জগতেও একটি নতুন দিক উন্মোচিত হয়েছে। সাধারণ ধাতুর মধ্যে ইলেক্ট্রনদের পারস্পরিক ক্রিয়া-প্রতিক্রিয়ার প্রভাব নিয়ে অনেক গবেষণা হয়েছে। কিন্তু ‘গ্রাফিন’-এর ইলেক্ট্রন আর সাধারণ ধাতুর ইলেক্ট্রনদের মধ্যে অনেক তফাৎ। আমরা দেখলাম, ‘গ্রাফিন’-এর ইলেক্ট্রনকে বুঝতে আলোর কাছাকাছি বেগের পদার্থবিদ্যা ব্যবহার করতে হয়। সেই আলোর কাছাকাছি গতিবেগের পদার্থবিদ্যা মানে যেসব ইলেক্ট্রন, তাদের মধ্যে পারস্পরিক ক্রিয়া জুড়ে দিলে কি হতে পারে, সেটি ঘনবস্তুর পদার্থবিদ্যার গবেষণায় একটি সম্পূর্ণ নতুন দিক।
তাই, নিঃসন্দেহে বলা যায়, ‘গ্রাফিন’ ঘনবস্তুর বিজ্ঞান জগতে একটি রীতিমতো হইচই সৃষ্টি করেছে।
(লেখাটি মূল ইংরাজি থেকে বাংলায় অনুবাদ করেছে অনির্বাণ গঙ্গোপাধ্যায়।)
তথ্যসূত্র ও অন্যান্য টুকিটাকি:
[১] আইনস্টাইন-এর স্পেশাল রিলেটিভিটি একটা ‘ক্লাসিকাল’ বা সনাতনী বর্ণনা। আমরা খালি চোখে যা দেখি বা তার থেকেও অনেক ছোট বস্তু, তাকে এই বর্ণনার সাহায্যে বোঝা যায়। কিন্তু ইলেক্ট্রন-এর মতো ক্ষুদ্রের জগতে চলে গেলে, তখন ‘কোয়ান্টাম বলবিদ্যা’-র শরণাপন্ন হতে হয়। ‘ক্লাসিকাল’ আর ‘কোয়ান্টাম’ জগতের সীমারেখাটা কোথায়, সেই নিয়ে ‘বিজ্ঞান’-এ লেখা ‘ক-এ কোয়ান্টাম’ পড়ুন।
[২] কেন বিশেষ আপেক্ষিকতাবাদ আর কোয়ান্টাম মেকানিক্স একে অপরের সাথে খাপ খায় না, সেটা জানতে হলে আগে বুঝতে হবে খাপ খাওয়া মানে কি। উদাহরণ হিসাবে তড়িৎ-গতিবিদ্যার ম্যাক্সওয়েলের সূত্রগুলি ধরা যায়। এই সূত্রগুলি বিশেষ আপেক্ষিকতাবাদের সাথে সামঞ্জস্যপূর্ণ। অর্থাৎ, এক ইনারশিয়াল রেফারেন্স ফ্রেম (inertial reference frame) থেকে আরেক ইনারশিয়াল রেফারেন্স ফ্রেম-এ যদি বিশেষ আপেক্ষিকতাবাদ মেনে যাওয়া যায়, তাহলে সূত্রগুলি অপরিবর্তিত থাকে। কেউ যদি দুটো আলাদা ইনারশিয়াল রেফারেন্স ফ্রেম-এ কোনো রাশি পরিমাপ করার জন্য পরীক্ষা করে, তাহলে একই উত্তর পাবে। ম্যাক্সওয়েলের সূত্র ছাড়াও আরো অনেক সূত্র এক ফ্রেম থেকে আরেক ফ্রেম-এ গেলে অপরিবর্তিত থাকে। কোয়ান্টাম মেকানিক্স-এর শ্রোডিংগার সূত্রটি এদের মধ্যে পড়ে না। অর্থাৎ, বিশেষ আপেক্ষিকতাবাদ মেনে রেফারেন্স ফ্রেম পরিবর্তন করলে অপরিবর্তিত থাকে না। যেহেতু আলোর গতির কাছাকাছি গতিতে ধাবমান কণাকে ব্যাখ্যা করতে বিশেষ আপেক্ষিকতাবাদ মানতেই হবে, তাই এদের ধর্ম শ্রোডিংগার সূত্র দিয়ে ব্যাখ্যা করা যায় না।
[৩] পরীক্ষার মাধ্যমে কোনো তত্ত্ব যাচাই করা গেলেই বিজ্ঞানে সেই তত্ত্বকে সফল হিসেবে ধরা হয়।
[৪] https://www.jstor.org/stable/24101915?seq=1#page_scan_tab_contents ও https://www.nature.com/nature/journal/v144/n3650/abs/144667a0.html
[৫] আন্দ্রে গাইম আর কনস্টান্টিন নোভোসেলভ-এর নোবেলজয়ী গ্রাফিন-সংক্রান্ত কাজ নিয়ে এখানে পড়ুন: https://science.sciencemag.org/content/306/5696/666 । লেখাটি বিনামূল্যে পাওয়া যায়, শুধু আপনাকে AAAS-এ একটা একাউন্ট খুলতে হবে।
[৬] Rev. Mod. Phys. 81, 109 (2009) – The electronic properties of graphene

khub interesting akta jinis khub sohojboddho bhabe bojhano hoyeche, lekhok k asonkho dhonnobaad.