আগে যা হয়েছেঃ
প্রথম পর্বে আমরা শুরু করেছিলাম জ্যামিতিতে আদৌ কিছু ‘দেওয়া আছে’ কিনা এই প্রশ্ন দিয়ে, দেখেছিলাম যে ইউক্লিডীয় জ্যামিতির স্বতঃসিদ্ধগুলো আসলে সেই দেওয়া থাকা জিনিসগুলো। কিন্তু কি বলছে সেগুলো? প্রথম পর্বে শুধুই প্রথম স্বতঃসিদ্ধ কি বলছে দেখেছিলাম। দ্বিতীয় পর্বে দেখেছি জ্যামিতির বীজগাণিতিকরণ হয়ে কিভাবে কার্তেসীয় স্থানাঙ্ক জ্যামিতি এল, আর এই স্থানাঙ্ক জ্যামিতির হাত ধরে আমরা দেখলাম যে দ্বিতীয়, তৃতীয় আর চতুর্থ স্বতঃসিদ্ধ কি বলছে। ইউক্লিডীয় দূরত্ব অপেক্ষক আর ইউক্লিডীয় ইনার প্রোডাক্ট কেও চিনলাম সেই পর্বেই। তৃতীয় পর্বে সমস্তটা জুড়েই আমরা মাথা ঘামিয়েছি পঞ্চম স্বতঃসিদ্ধ নিয়ে। দেখলাম পঞ্চম স্বতঃসিদ্ধ কি বলছে আর দেখেছি সেই স্বতঃসিদ্ধ কে পালটে নিলেও আমরা জ্যামিতি পাই, শুধু সেই জ্যামিতি আর ইউক্লিডীয় জ্যামিতি নয়, অনিউক্লিডীয় জ্যামিতি। চতুর্থ পর্বে আমরা দেখেছি অনিউক্লিডীয় জ্যামিতির অদ্ভুত অথচ মজার জগতটাকে। একই সাথে চতুর্থ পর্বের শেষে উঠে এসেছে নতুন প্রশ্ন –
অনিউক্লিডীয় জ্যামিতিরও কি বীজগাণিতিকরণ সম্ভব?
এই প্রশ্নের উত্তর প্রথম দিয়েছিলেন রীমান, ইংরেজি ১৮৫৪ সালে গটিনগেন বিশ্ববিদ্যালয়ে এক বক্তৃতায়। দেড় শতাব্দীর উপর পাড়ি দিয়েও সেই উত্তরই আজও আধুনিক অবকলন জ্যামিতির (differential geometry) মূল কথা। এই পর্বে আমরা সেই বৈপ্লবিক উত্তরটা বোঝার চেষ্টা করব।
[ পঞ্চম পর্বের সংক্ষিপ্তসারঃ
রীমানের উত্তর আমাদের জ্যামিতি সংক্রান্ত ধ্যানধারণায় একটা বিপ্লব। অথচ মূল ধারণাগুলো ভীষণ জটিল তা নয়, ধাপে ধাপে এগোলেই আমরা মোটামুটি সহজেই রীমানের যুক্তিক্রম অনুসরণ করতে পারব। কিন্তু সেজন্যে একটা জরুরী জিনিস প্রথম থেকেই মাথায় রাখা দরকার যে আমরা ঠিক কি করতে চাইছি আর সেজন্যে আমাদের কি কি লাগবে। প্রথমেই আর একবার ঝালিয়ে নেওয়া যাক ইউক্লিডীয় জ্যামিতির বীজগাণিতিকরণের ক্ষেত্রে ঠিক কি কি করেছি (দ্বিতীয় পর্ব দেখুন)।
- আমরা শুরু করেছিলাম ইউক্লিডীয় স্থান নিয়ে, যেটাকে একটা লিনিয়ার স্থান বা ভেক্টর স্থান হিসেবে ভাবা যায়।
- সেই স্থানের প্রতিটি বিন্দুর অবস্থান নির্ধারণের জন্যে আমরা স্থানাঙ্কের ধারণা এনেছি, অর্থাৎ একটা বিন্দুকে মূলবিন্দু বলে বেছে নিয়েছি এবং কিছু স্থানাঙ্ক অক্ষ বেছে নিয়েছি, তারপর সেই মূলবিন্দু ও অক্ষের সাপেক্ষে প্রতিটি বিন্দুর একটা স্থানাঙ্ক ব্যবহার করেছি ( কার্তেসীয় স্থানাঙ্ক জ্যামিতি ) ।
- ওই লিনিয়ার স্পেসে যেকোন দুটো ভেক্টরের মধ্যে কোণ মাপার জন্য একটা ইনার প্রোডাক্ট ব্যবহার করেছি – ইউক্লিডীয় ইনার প্রোডাক্টটা। আবার দেখেছি যে এই ইনার প্রোডাক্টটাই আমরা দূরত্ব মাপার কাজেও লাগাতে পারি, অর্থাৎ এই ইনার প্রোডাক্টটাই আমাদের দূরত্ব মাপার রুলারটা, ইউক্লিডীয় দূরত্ব অপেক্ষকটা দেয়।
আমরা আগেই দেখেছি (চতুর্থ পর্ব দেখুন) যে অনিউক্লিডীয় জ্যামিতিরা আসলে বাঁকা জিনিসের ওপর জ্যামিতি। তাই অনিউক্লিডীয় জ্যামিতির ক্ষেত্রে ওপরের ধাপগুলো একে একে করে ফেলার চেষ্টা করতে গেলে প্রথমেই সমস্যা আসবে যে বাঁকা জিনিসের ওপরে লিনিয়ার স্থান কোথায় পাব। ইউক্লিডীয় স্থানকে লিনিয়ার স্থান হিসেবে ভাবা যায়, কিন্তু কোন বাঁকা জিনিস ( যেমন ধরা যাক গোলকের উপরিতলটা ) নিজে মোটেই লিনিয়ার স্থান নয়, হতেও পারে না। মূলবিন্দুকে কেন্দ্র করে আঁকা গোলকটার উপরিতলে দুটো আলাদা আলাদা বিন্দুর অবস্থান সদিশের কথা ভাবুন। তাদের ভেক্টর যোগফল যে বিন্দুর অবস্থান সদিশ সেই বিন্দুটা আদৌ গোলকটার উপরিতলে থাকবে না। অথচ লিনিয়ার স্থান আমাদের খুবই দরকার, কারণ ওপরের তৃতীয় ধাপ আবার খেয়াল করলেই দেখবেন আমরা কোণ মাপতে চাই ইনার প্রোডাক্ট দিয়ে, এমনকি দূরত্বও – অথচ ইনার প্রোডাক্ট একটা লিনিয়ার স্থানে দুটো ভেক্টরের মধ্যে কোণ মাপে। লিনিয়ার স্থান না থাকলে ইনার প্রোডাক্টের ধারণা অর্থহীন। তাই প্রথম ধাপের সমস্যা সমাধান না করে তৃতীয় ধাপের সমস্যা, অর্থাৎ ইনার প্রোডাক্ট বসানোর সমস্যা নিয়ে আমরা আপাতত মাথা ঘামানোর জায়গায় এখনো নেই।
দ্বিতীয় ধাপের সমস্যা আবার অন্যজায়গায়, যদিও আগের সমস্যাটার সাথে তার গভীর সম্পর্ক আছে। সমস্যাটা হল ওই বাঁকা জিনিসের প্রতিটা বিন্দুর স্থানাঙ্ক দেওয়ার।
ইউক্লিডীয় স্থানের মত আর একটাই স্থানাঙ্ক তন্ত্র ব্যবহার করে আর কাজ চলবে না বাঁকা জিনিসের ক্ষেত্রে।
এই পর্বে আমরা এই প্রথম দুই ধাপের সমস্যা নিয়ে মাথা ঘামাব। আমরা দেখব যে এই দুই সমস্যাই সমাধান হবে কিছুটা একই ভাবে। একটাই স্থানাঙ্ক তন্ত্র যা গোটা স্থানেই কার্যকরী এরকম কিছুর বদলে আমরা কাজ চালাব আঞ্চলিক স্থানাঙ্ক তন্ত্র দিয়ে। নিচের স্থানকে অসংখ্য তাপ্পিমারা একটা নকশিকাঁথার মত জিনিস ভাবব আর প্রতিটা তাপ্পিতে ব্যবহার করা যাবে এরকম আঞ্চলিক স্থানাঙ্ক তন্ত্র চাইব। আবার একইভাবে, গোটা স্থানটা যেহেতু লিনিয়ার স্থান হতে পারে না তাই সেইটা চাওয়ার বদলে আমরা ওই স্থানের প্রতিটি বিন্দুতে একটা করে লিনিয়ার স্থান আছে চাইব। আমরা দেখব যে এমনকি বাঁকা জিনিসের ক্ষেত্রেও প্রতিটি বিন্দুতে একটা লিনিয়ার স্থান আমরা পেতে পারি– সেইটাই ওই বিন্দুতে ওই স্থানের স্পর্শক স্থান, অর্থাৎ ওই বিন্দুতে জমি-স্থানের সবকটা স্পর্শকগুলোর সমষ্টিটা । আরও দেখব যে এই নিচে জমি হিসেবে একটা স্থান আর তার উপরে প্রতিটি বিন্দুতে একটা করে স্থান, এই ব্যাপারটা যা ভাবনায় অনেকটা খড়ের গোছার মত জিনিস, অঙ্কের ভাষায় একে বলা হয় তন্তুগুচ্ছ। ]
চ্যাটালো নাকি ‘লোকালি’ চ্যাটালো ?
প্রথমে আমরা দেখব বাঁকা জিনিসের ওপরে স্থানাঙ্ক দেওয়ার সমস্যা কিভাবে সমাধান হল। রীমান ভাবতে শুরু করলেন একটা ছোট পর্যবেক্ষণ থেকে যে যেকোনো বাঁকা জিনিসেরই খুব ছোট অংশ দেখলে সেটা বাঁকা নয়, চ্যাটালো (flat), অর্থাৎ ইউক্লিডীয় স্থানের ছোট অংশের মতই দেখতে। ঠিক যেমন পৃথিবীর উপরের তল, যেখানে আমরা বাস করি, সেটা আসলে বাঁকা, গোলকের উপরিতলের মত। কিন্তু আমরা যতদূর দেখতে পাই খালি চোখে, সেটা এতই ছোট্ট একটা অংশ যে সেগুলোকে আমরা দ্বিমাত্রিক সমতলের মতই দেখি। রীমান বুঝেছিলেন যে এই ধর্মটা আসলে আমাদের জ্যামিতি করার জন্যে খুবই গুরুত্বপূর্ণ।১ তাই তিনি ঠিক করলেন যে তিনি তার জ্যামিতি করবেন যে সমস্ত স্থানের উপর তাদের সবারই যেন এই ধর্মটা থাকে।
আমরা যতদূর দেখতে পাই খালি চোখে, সেটা এতই ছোট্ট একটা অংশ যে সেগুলোকে আমরা দ্বিমাত্রিক সমতলের মতই দেখি।
এই ধর্মটার একটা নাম আছে অঙ্কে, এরকম স্থানকে আমরা বলি আঞ্চলিকভাবে ইউক্লিডীয় স্থান ( locally euclidean space )।২
ম্যানিফোল্ড মানে নকশী কাঁথা
আসলে আমাদের আঞ্চলিকভাবে ইউক্লিডীয় স্থানের থেকে একটু বেশী কিছু দরকার, সেটা হলো “মসৃণত্ব”। কেন দরকার? স্থানটা মসৃণ না হলে আসলে ওই স্থানের প্রতিটি বিন্দুতে স্পর্শক টানার সমস্যা। স্পর্শক কেন টানতে চাইছি বুঝতে আমাদের আর একটু অপেক্ষা করতে হবে, একটু পরের স্পর্শক স্থানের আলোচনার জন্য। আপাতত ততক্ষণ পর্যন্ত মসৃণত্ব প্রয়োজনীয় এই তথ্যটুকু মাথায় রাখলেই হবে। কিন্তু মসৃণত্ব মানে কি? মানে যে জিনিসটার ওপর জ্যামিতি করব, তা বাঁকা হতে পারে, কিন্তু মসৃণভাবে বাঁকা, হঠাৎ করে কোণা তৈরি করে বাঁকলে চলবে না। নিচের ছবিতে তফাতটা বোঝা যাবে। একদম বাঁদিকেরটা অবশ্যই গোলকের উপরিতল, মসৃণ জিনিস। কিন্তু অন্য দুটো নয়, দুটোরই ওই খাঁজ পড়া জায়গাটায় ওই তলগুলো আর মসৃণ নয়।
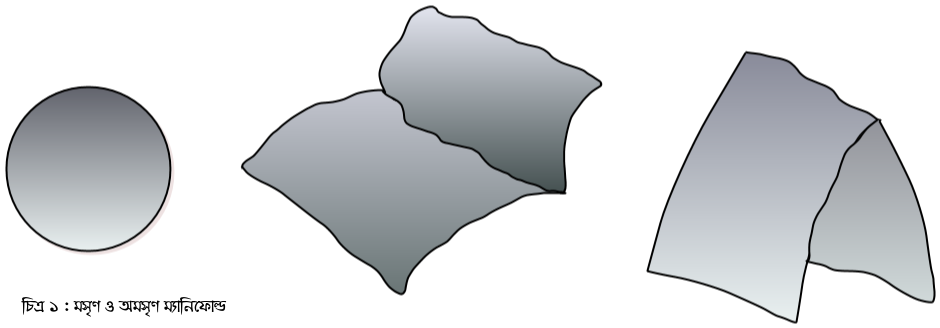
এইরকম মসৃণ আঞ্চলিকভাবে ইউক্লিডীয় স্থানকে অঙ্কের ভাষায় বলে স্মুদ ম্যানিফোল্ড ( smooth manifold )। ম্যানিফোল্ড শব্দটার সাধারণ কথ্য ইংরাজিতে ঠিক কোন মানে নেই, রীমানের ব্যবহৃত মূল জার্মান শব্দটির মানে হরেকরকমবা বা পাঁচমিশালী কিছু একটা, ম্যানিফোল্ড শব্দটা তারই একটা টেকনিকাল প্রতিশব্দ মাত্র। ম্যানিফোল্ডকে আমরা ভাবতে পারি একটা নকশীকাঁথার মত, অসংখ্য ইউক্লিডীয় স্থানের ছোট ছোট টুকরো নানানরকম ভাবে বেঁকিয়ে-চুরিয়ে (কিন্তু মসৃণভাবে, কোন কোণা না তৈরি করে ফেলে) তারপর সেগুলোকে একসাথে সেলাই করা একটা কাঁথা। ওই ইউক্লিডীয় স্থানের ছোট ছোট টুকরোগুলো দিয়েই আমরা বাঁকা জিনিসের ওপরে স্থানাঙ্ক জ্যামিতি করতে পারি, আর সেই টুকরোগুলো ওই কাঁথার ওপরে অসংখ্য তাপ্পির মত। কিভাবে করতে পারি? টেকনিক্যালি যেভাবে করা হয় সেটাকে বলে স্থানাঙ্ক পরিবর্তন বা কোঅর্ডিনেট ট্রান্সফর্মেশন ( co-ordinate transformation), কিন্তু সেসবের কচকচি ছেড়ে আমরা মূল ধারণাটা বুঝব।
ম্যানিফোল্ডকে আমরা ভাবতে পারি একটা নকশীকাঁথার মত,অসংখ্য ইউক্লিডীয় স্থানের ছোট ছোট টুকরোএকসাথে সেলাই করা একটা কাঁথা। যেহেতু টুকরোগুলো ইউক্লিডীয় স্থানের টুকরো, তাই তাদের উপরে ইউক্লিডীয় স্থানাঙ্ক ব্যবহার সম্ভব। ঠিক সেইটাই ব্যবহার করব আমরা। বাঁকা জিনিসটার ওপরে কোন একটা বিন্দুর, ধরা যাক বিন্দুটার নাম x, আর তার চারপাশে একটা তাপ্পির কথা ভাবি। ওই তাপ্পির উপরে অন্য কোন একটা বিন্দুর, ধরা যাক সেই বিন্দুর নাম y, তার স্থানাঙ্ক বার করতে ওই তাপ্পিটাকে আবার ইউক্লিডীয় স্থানে বসাবো, মানে যেভাবে বেঁকিয়ে-চুরিয়ে ইউক্লিডীয় স্থানের টুকরোটা তাপ্পি হয়ে বসে গেছিল তার ঠিক উল্টোটা করে, এককথায় বাঁকা ব্যপারটাকে সোজা করে নিয়ে। এইবারে x বিন্দুটা ইউক্লিডীয় স্থানে যেখানে গিয়ে পড়ল সেইটাকে মূলবিন্দু ধরে সেইখানে ইউক্লিডীয় স্থানাঙ্ক তন্ত্র বসাব, আর সেই স্থানাঙ্ক অনুযায়ী y বিন্দুটা যেখানে এসে পড়েছে তার স্থানাঙ্ক বার করব। সেইটাই y বিন্দুর ওই তাপ্পিতে আঞ্চলিক স্থানাঙ্ক।
ম্যানিফোল্ডকে আমরা ভাবতে পারি একটা নকশীকাঁথার মত,অসংখ্য ইউক্লিডীয় স্থানের ছোট ছোট টুকরোএকসাথে সেলাই করা একটা কাঁথা।
অন্যভাবেও ভাবা যায় পদ্ধতিটাকে। ইউক্লিডীয় স্থানের মূলবিন্দুর চারপাশে একটা টুকরোকে ভাবুন আর কল্পনা করে নিন যে ইঙ্কলিডীয় স্থানাঙ্কগুলো তার গায়ে এঁকে দেওয়া আছে, গ্রাফ কাগজের (printed graph paper) মত। এরপর ওই টুকরোটাকে বেঁকিয়ে-চুরিয়ে যখন বাঁকা স্থানের উপরে তাপ্পি হিসেবে ফেলব, তখন ওই আঁকা গ্রাফ লাইনগুলো, যেগুলোও এখন বেঁকে গেছে, সেইগুলো দেখে দেখেই স্থানাঙ্ক বার করব। পৃথিবীর ওপরেও আমরা এইটাইই করি আসলে। মানচিত্রে অক্ষাংশ দ্রাঘিমাংশের লাইনগুলো গ্রাফ কাগজের মতই লাগে, অথচ পৃথিবীর উপরিতলে সেগুলো বাঁকা। আবার উপমাটা পুরোটা ঠিক নয়, কারণ মানচিত্রে দূরত্বের প্রশ্নটা জরুরী, পুরো পৃথিবীর মানচিত্র এভাবে করলে দূরত্ব হিসেব করতে ভুল হবে, কারণ মেরুদুটোর কাছাকাছি দুটো দ্রাঘিমারেখার মধ্যে দূরত্ব অনেক কম, দুই মেরুতে শূন্য, তাই দ্রাঘিমারেখাদের সমান্তরাল করে আঁকলে গোটা পৃথিবীর সঠিক মানচিত্র আঁকা সম্ভব নয়।৩ কোন বিন্দুর স্থানাঙ্ক নির্ধারণের জন্য দূরত্ব সংক্রান্ত গাণিতিক তথ্য বা “মেট্রিক” (metric) আদৌ জরুরী নয়, কিন্তু তাহলেও গোলকের উপরিতলে বা কোন বাঁকা জিনিসে কোন একটাই স্থানাঙ্ক-তন্ত্র দিয়ে সব বিন্দুর স্থানাঙ্ক পাওয়া সম্ভব না। ভেবে দেখুন মানচিত্রেও দুই মেরুর কোন নির্দিষ্ট দ্রাঘিমাংশ নেই,৪ ঠিক এই কারণেই আমরাও আঞ্চলিক স্থানাঙ্ক ব্যবহার করছি। যাই হোক, যেহেতু এই তাপ্পিগুলো আসলে আঞ্চলিক স্থানাঙ্ক দেয়, তাই এদেরকে স্থানাঙ্ক তাপ্পি বা কোঅর্ডিনেট প্যাচ ( co-ordinate patch ) বলা হয়। অনেকসময় এদেরকে স্থানাঙ্ক নকশা অথবা কোঅর্ডিনেট চার্ট ( co-ordinate chart ) ও বলা হয়, আর সবকটা নকশা একসাথে মিলিয়ে যেটা তৈরী হয় সেটাকে স্থানাঙ্ক মানচিত্র বা কোঅর্ডিনেট অ্যাটলাস ( co-ordinate atlas ) বলে। ইউক্লিডীয় স্থানের সাথে এখানে তফাত হচ্ছে ইউক্লিডীয় স্থানে একটা স্থানাঙ্ক-তন্ত্র ( co-ordinate system ) দিয়েই সর্বত্র কাজ চলে, মানে একবার মূলবিন্দু আর অক্ষগুলো বেছে নিলে গোটা ইউক্লিডীয় স্থানেই স্থানাঙ্ক পাই। এখানে তেমন নয় ব্যাপারটা। এক একটা তাপ্পির মধ্যে এক একটা স্থানাঙ্ক-তন্ত্র আছে। এদেরকে বলে আঞ্চলিক স্থানাঙ্ক-তন্ত্র বা লোকাল কোঅর্ডিনেট সিস্টেম ( local co-ordinate system)। আর এই স্থানাঙ্ক-তন্ত্রগুলো এমনভাবেই সংজ্ঞায়িত যে একটা অঞ্চল যদি একটার বেশী তাপ্পিতে থাকে তাহলে কোন তাপ্পির স্থানাঙ্ক-তন্ত্র ব্যবহার করছি তাতে কিছু আসে যায় না। কিন্তু সর্বত্র কাজ চালানোর মত একটাই স্থানাঙ্ক-তন্ত্র বা গ্লোবাল কোঅর্ডিনেট সিস্টেম ( global co-ordinate system ) নাও থাকতে পারে।
স্থানাঙ্ক নাহয় দিতে পারলাম, অর্থাৎ প্রথমে যে দুটো সমস্যার কথা বলেছিলাম তার একটা সমাধান হল। কিন্তু এইবার এখানে একটা মুশকিল আছে, আঞ্চলিকভাবে ইউক্লিডীয় স্থানেরা কিন্তু আর লিনিয়ার স্পেস নয়। তাই প্রথম সমস্যাটা, অর্থাৎ ইনার প্রোডাক্ট বসানোর জন্য লিনিয়ার স্পেস কোথায় পাব, সেই সমস্যাটা থেকেই গেল।
একটা অঞ্চল যদি একটার বেশী তাপ্পিতে থাকে তাহলে কোন তাপ্পির স্থানাঙ্ক-তন্ত্র ব্যবহার করছি তাতে কিছু আসে যায় না। তবে এটাও খুব একটা বড়সড় মুশকিল নয়। কারণ বস্তুত ইউক্লিডীয় স্থানও আসলে লিনিয়ার স্পেস নয়। আগেই বলেছিলাম যে ইউক্লিডীয় স্থানের বিন্দুগুলোর ‘পজিশন ভেক্টর’ গুলোকে নিলে সেইটা লিনিয়ার স্পেস গঠন করে, শুধু এইভাবে কেন বললাম সেইটা খুব স্পষ্ট করে বলিনি, আপনারা কি কেউ তখন খেয়াল করেছিলেন যে দুটো আসলে আলাদা কথা?
একটা অঞ্চল যদি একটার বেশী তাপ্পিতে থাকে তাহলে কোন তাপ্পির স্থানাঙ্ক-তন্ত্র ব্যবহার করছি তাতে কিছু আসে যায় না।
সব ভেক্টররা ভেক্টর নয়
এই আলাদা হওয়ার মধ্যে আসলে লুকিয়ে আছে পদার্থবিদ্যার ভেক্টর আর অঙ্কের ভেক্টরের মধ্যে পার্থক্য। তফাতটা বোঝা খুব শক্ত নয়, একটা উদাহরণ দিলেই পরিষ্কার হয়ে যাবে। ধরা যাক ত্রিমাত্রিক ইউক্লিডীয় স্থানে আপনি যেকোনো দুটো বিন্দু নিলেন, ধরুন তাদের নাম A আর B। এইবারে আপনি যদি A থেকে Bপর্যন্ত একটা তীর আঁকেন তাহলে সেই তীরটাই AB ভেক্টর, কিন্তু অঙ্কে এটাকে ভেক্টর বলতে গেলে ওই A বিন্দুটাকে মূলবিন্দু অর্থাৎ origin, মানে যার স্থানাঙ্ক (0,0,0), সেই বিন্দুটা হতে হবে, নইলে চলবে না।৫ ইউক্লিডীয় স্থানের প্রতিটি বিন্দুর ‘পজিশন ভেক্টর’রা লিনিয়ার স্থান বা ভেক্টর স্থান গঠন করে। কারণ অবস্থান সদিশ বা ‘পজিশন ভেক্টর’ (position vector) বলা হচ্ছে মানেই একটা নির্দিষ্ট মূলবিন্দু বেছে নেওয়া হয়েছে আর সেই মূলবিন্দুর সাপেক্ষেই অন্য যেকোন বিন্দুর অবস্থান মাপা হচ্ছে, মূলবিন্দু থেকে সেই বিন্দু পর্যন্ত একটা ভেক্টর এঁকে। তাই যেকোন অবস্থান সদিশেরই শুরুর বিন্দু মূলবিন্দুটা। কিন্তু ইউক্লিডীয় স্থান নিজে লিনিয়ার স্থান নয়, কারণ ইউক্লিডীয় স্থানে এরকম কোন সুনির্দিষ্ট মূলবিন্দু নেই। এমনকি এমন কোন একটা বিন্দুও নেই যেটাকে মূলবিন্দু বলে পছন্দ করা স্বাভাবিক। এরকম জিনিসকে অঙ্কে বলে অ্যাফাইন স্থান বা affine space। অ্যাফাইন শব্দটার মানে আসলে সরলরৈখিকই, আবার লিনিয়ার মানেও তাই… কিন্তু সাধারণ কথ্য ইংরেজিতে তফাত না থাকলেও অঙ্কে এই শব্দদুটোর মানে আলাদা।
দুজনকে যদি একটা বিন্দু দেখিয়ে জিগ্যেস করা হয় বিন্দুটা কোথায়, দুজনের মূলবিন্দু যেহেতু আলাদা, তাই তাদের উত্তরও আলাদা হবে। কি তফাত? কেনই বা তফাত? হঠাৎ মূলবিন্দু নিয়েই বা মাথা ঘামাব কেন? মাথা ঘামানোর একটা কারণ মোটামুটি সহজ। আমরা ছোটবেলায় পদার্থবিদ্যার অঙ্ক কষতে গিয়ে দেখেছি যে মূলবিন্দুকে আমাদের সুবিধেমত যেকোনো জায়গায় বসানো যায়, অঙ্কে স্থানাঙ্ক জ্যামিতির ক্ষেত্রেও দেখেছি, মূলবিন্দু আমরা আমাদের সুবিধেমত ধরে নিতে পারি, তাতে অঙ্কের শেষ ফলাফল পাল্টায় না। বিষয়টা সামান্য অন্যভাবেও ভাবা যায়, ভেবে নিন আপনি পর্যবেক্ষক, কোন একটা ঘটনা লক্ষ করছেন। এবার এই পর্যবেক্ষণকে লিখে ফেলতে আপনি আপনার সুবিধেমত মূলবিন্দু ও স্থানাঙ্ক অক্ষ বেছে নেবেন— আর তাতে আপনি নিজে যেখানে রয়েছেন সেই বিন্দুকেই মূলবিন্দু ধরে নেওয়া প্রায়শই সবচেয়ে সুবিধেজনক। আবার আর একজন একই ঘটনা দেখছেন, তাঁর পর্যবেক্ষণের মূলবিন্দু তিনি যেখানে দাঁড়িয়ে। দুজনকে যদি একটা বিন্দু দেখিয়ে জিগ্যেস করা হয় বিন্দুটা কোথায়, দুজনেই ধরা যাক বিন্দুটার কোঅর্ডিনেট বা স্থানাঙ্ক বলবেন। দুজনের মূলবিন্দু যেহেতু আলাদা তাই তাদের উত্তরও আলাদা হবে। তাহলে কে ঠিক? অবশ্যই দুজনেই, কারণ দুজনেই নিজেদের সাপেক্ষে বিন্দুটার অবস্থান বলছেন মাত্র। কোন একজনেরটা আলাদা করে বেশী ঠিক মনে করার কোন যুক্তি নেই। কিন্তু গাণিতিকভাবে দুজনেই ঠিক কথাটার একটাই অর্থ হয়, যে দুজনের বক্তব্যই একদমই তুল্যমুল্য (completely equivalent )। সত্যিই তাই-ই, আমরা যদি দুজনের পরস্পরের সাপেক্ষে অবস্থান জানি তাহলে একজনের বলা বিন্দুটার অবস্থান থেকে অন্যজনের সাপেক্ষে বিন্দুটার অবস্থানও আমরা সহজেই বার করতে পারব।
দুজনকে যদি একটা বিন্দু দেখিয়ে জিগ্যেস করা হয় বিন্দুটা কোথায়, দুজনের মূলবিন্দু যেহেতু আলাদা, তাই তাদের উত্তরও আলাদা হবে।
অর্থাৎ মূলবিন্দু বেছে নেওয়ায় আমাদের স্বাধীনতা আছে, থাকা উচিৎ ও। কিন্তু একটা ভেক্টর স্পেস মানে তার একটা নির্দিষ্ট মূলবিন্দু থাকতেই হবে, সেটা খুশিমত বেছে নিতে আমরা পারি না। তাহলে এখানে কি করে পারছি? পারছি আসলে অন্য একটা কারণে। ধরে নিন আপনি আর আমি দাঁড়িয়ে আছি ত্রিমাত্রিক ভৌত স্থানে ( 3 dimensional physical space )। এর আগে -কে ত্রিমাত্রিক ইউক্লিডীয় স্থান বলেছি, কিন্তু এখন আমরা সাবধানে পা ফেলব।
আসলে ত্রিমাত্রিক বাস্তব কার্তেসীয় প্রোডাক্ট স্থান ( 3 dimensional real Cartesian product space) । কার্তেসীয় প্রোডাক্ট স্থান মানে কী? যদি A এবং B দুটো সেট হয়, তাহলে (a,b) কে আমরা বলব একটা সাজানো ক্রমিক জোড় ( ordered pair ) যদি এই একজোড়া জিনিসের প্রথমটা অর্থাৎ a জিনিসটা A সেট এর হয়, আর দ্বিতীয়টা, অর্থাৎ b জিনিসটা B সেট এর হয়। এইবারে এইরকম সমস্ত সাজানো জোড় এর সেটটাকে বলব A ও B সেটের কার্তেসীয় প্রোডাক্ট, গাণিতিক চিহ্নে লেখা হয় AB । অর্থাৎ এইভাবে দেখলে
হচ্ছে বাস্তব সংখ্যাদের সেটকে তিনবার নিয়ে তাদের কার্তেসীয় প্রোডাক্ট। ওপরের অংশটা থেকে একটু ভাবলেই বুঝবেন তার মানে
-র যেকোন বিন্দু আসলে একটা ক্রমিক সংখ্যাত্রয় (x,y,z), যেখানে x,y,z তিনটেই বাস্তব সংখ্যা। এই সংখ্যাগুলো হচ্ছে ওই বিন্দুটার স্থানাঙ্ক, কো-অর্ডিনেট। কার সাপেক্ষে? আমি যে
টা দেখছি সেটায় আমার সাপেক্ষে, মানে আমি যেখানে দাঁড়িয়ে সেই বিন্দুটাকে মূলবিন্দু ধরে আর অক্ষগুলোকে বেছে নিয়ে। আপনি যে
-টা দেখছেন সেটার মূলবিন্দু আপনি যেখানে দাঁড়িয়ে সেই বিন্দুটা, আর অক্ষ আপনি যেভাবে বেছেছেন। তাই আপনি আমি দুজনেই ত্রিমাত্রিক ভৌত স্থানে ( physical space ) এ দাঁড়িয়ে ঠিকই, কিন্তু দুজনে একই
তে দাঁড়িয়ে নেই। আপনার নিজের একটা
আছে, আবার আমারও নিজের একটা
আছে। আমি যদি হেঁটে আপনার জায়গায় চলে যাই আর গিয়ে অক্ষগুলোকে ঘুরিয়ে আপনার অক্ষগুলোর সাথে মিলিয়ে নি, তাহলে তখন আমার
আর আপনার
-টা একই হয়ে যাবে।
তাই আমাদের ভৌত স্থান কিম্বা ত্রিমাত্রিক ইউক্লিডীয় স্থান আসলে মোটেই 3, বা ত্রিমাত্রিক কার্তেসীয় প্রোডাক্ট স্থান নয়, বরং জমি হিসেবে নীচে একটা 3আছে, আর 3 র প্রতিটি বিন্দুর উপরে একটা করে 3 বসানো আছে ভাবা যেতে পারে, এমনভাবে যেন A বিন্দুকে টেনে B বিন্দুর জায়গায় নিয়ে গেলে Aর 3 টাকেও ঘুরিয়ে Bর 3 টার সাথে মিলিয়ে দেওয়া যায়।
এই মিলিয়ে দেওয়া ব্যাপারটা জরুরী আর খুব মজারও। কিন্তু এইটায় আমরা পরে ফিরে আসব, তার আগে দেখে নিই যে এই বাঁকা জিনিসের ক্ষেত্রে এইরকম প্রতিটি বিন্দুতে একটা লিনিয়ার স্থান পাওয়া যায় কিনা। ইউক্লিডীয় স্থানের ক্ষেত্রে নীচের জমিটাও লিনিয়ার স্থান, প্রতিটি বিন্দুতেও একটা করে লিনিয়ার স্থান আছে। বাঁকা জিনিসের ক্ষেত্রে নীচের জমিটা লিনিয়ার স্থান হবে না, কিন্তু প্রতিটি বিন্দুতে একটা লিনিয়ার স্থান হয়ত এক্ষেত্রেও পেতে পারি। বস্তুত এমন স্থান আসলে আমাদের হাতে আছে। প্রতিটি বিন্দুতে সেই বিন্দুতে স্পর্শক বা ট্যানজেন্টগুলোর সমষ্টিটা – অঙ্কে যার নাম স্পর্শক স্থান।
স্পর্শক স্থান
স্পর্শক কাকে বলে আমরা সবাই খানিকটা জানি, স্কুলের জ্যামিতি থেকে অন্তত বৃত্তের স্পর্শক আমরা এঁকেছি, হয়ত স্পর্শক কি মনে রাখার চুটকিটাও৬ আমাদের অনেকেরই মনে পড়বে, কিন্তু সেসবই দ্বিমাত্রিক জ্যামিতির স্পর্শক। ত্রিমাত্রিক জ্যামিতিতে স্পর্শক হয়? মানে একটা বক্ররেখা, যেটা আর কাগজের তলে আটকে নেই, সেরকম রেখারও স্পর্শক হয় কি? হয়। আসলে পদ্ধতিটাও খুব আলাদা কিছু নয়, কারণ রেখাটা যতই তিনমাত্রায় বেঁকে থাকুক না কেন, যে বিন্দুতে স্পর্শক আঁকব সেই বিন্দুর আশেপাশে রেখাটার একটা খুব ছোট্ট অংশকে কল্পনা করলে বোঝা যায় সেটা মোটামুটি ভাবে একটা তলেই আছে। এই ‘খুব ছোট্ট’ আর ‘মোটামুটি’ শব্দদুটো শুনে যা মনে হচ্ছে ব্যাপারটা আদৌ সেরকম অনির্দিষ্ট কিছু নয় আসলে। অঙ্কে ‘ইনফাইনিটেসিমাল’ বা ‘অসীম ছোট’ আর ‘সীমা’ বা ‘লিমিট’ এর ধারণা ব্যবহার করে এইটাকে খুব নির্ভুলভাবেই লেখা যায়, আর সেই ধারণাগুলোই কলনবিদ্যা বা ক্যালকুলাস এর গোড়ার কথা। কিন্তু আমরা আপাতত ধারণাগুলোকে বুঝতে চাইছি, একদম নিখুঁত নিশ্ছিদ্র গাণিতিক যুক্তিজাল নিয়ে মাথা না ঘামিয়ে।
আমরা একটা বক্ররেখার স্পর্শক কাকে বলে বুঝবো, শুধুই ধারণার জায়গা থেকে। একটা বক্ররেখা, যেকোন মাত্রার যেকোন রকম স্থানেই হোক, সেটাকে আমরা একটা বিন্দুর সঞ্চারপথ (locus) বলে ভাবতে পারি, বিন্দুর জায়গায় একটা কণাও ভাবতে পারেন, কোন তফাত নেই। শুধু একটাই মুশকিল আছে, রেখার উপরে কোন একটা বিন্দু ভাবলে ওই কণাটা সেই বিন্দুটায় দুদিক থেকে আসতে পারে।
একটা বক্ররেখাকে আমরা একটা বিন্দু বা কণার সঞ্চারপথ (locus) বলে ভাবতে পারি। আপাতত যেকোন একটা দিক বেছে নিন। বক্ররেখাটায় কোণা, খোঁচা এইসব না থাকলে স্পর্শকরেখাটা একই হবে যেদিকই বাছুন, আর স্পর্শক ভেক্টরদুটো সেই রেখা বরাবর একটা আর একটার উলটো হবে৭। এই কোণা, খোঁচা না থাকার দরকারের জন্যই এর আগে আঞ্চলিকভাবে ইউক্লিডীয় স্থানের আলোচনায় বলেছিলাম মসৃণত্ব প্রয়োজনীয়।
একটা বক্ররেখাকে আমরা একটা বিন্দু বা কণার সঞ্চারপথ (locus) বলে ভাবতে পারি।
এইবারে একটা বিন্দুতে স্পর্শক আঁকতে কণাটা সেই বিন্দুতে পৌঁছলে তাকে থামিয়ে দিন, দিয়ে ঠিক সেই যেদিকে যাচ্ছিল সেই বরাবর একটা সরলরেখা৮ টানুন, সেইটাই ওই বিন্দুতে ওই বক্ররেখার স্পর্শক।
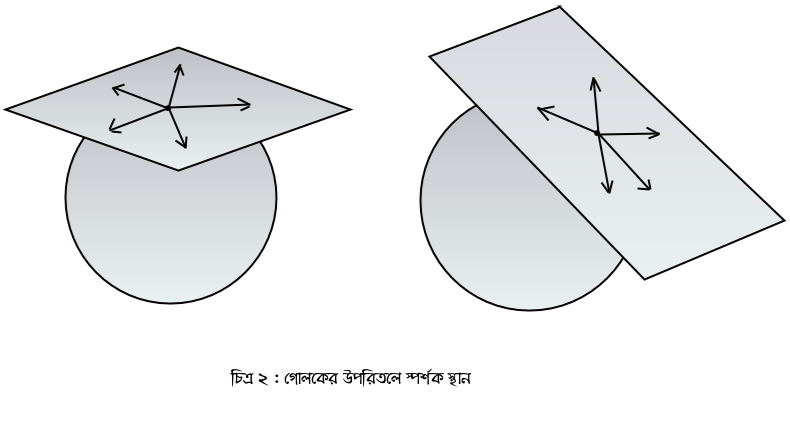
এইবার একটা বাঁকা জিনিসের কথা ভাবা যাক। আবারও গোলকের উপরিতলটাকেই নেওয়া যাক উদাহরণ হিসেবে। এই তলের উপরে কোন একটা বিন্দু বেছে নিন। এইবার ওই বিন্দু দিয়ে গোলকের উপরের তলে কতগুলো বক্ররেখা আঁকা যায়? অসীম সংখ্যক। এইবারে সেই সব বক্ররেখাগুলোর ওই বিন্দুতে স্পর্শক আঁকুন। এইরকম সব স্পর্শকগুলোকে নিন। সেইটাকেই ওই বিন্দুতে গোলকের উপরিতলের উপরের ‘স্পর্শক স্থান’ বা ট্যানজেন্ট স্পেস ( tangent space )। কেমন দেখতে সেটা? একদম দ্বিমাত্রিক সমতলের মতই, শুধু কোন বিন্দুতে আঁকছেন তার ওপর নির্ভর করে একটু হেলানো। একটা বল আর কাগজ নিয়ে নিজেরা সহজেই করে দেখতে পারবেন। নিচে ছবি দেখলে বিষয়টা স্পষ্ট হবে।
খেয়াল করে দেখুন প্রতিটি বিন্দুতেই স্পর্শক স্থানটা ওই কাগজটার মতই দেখতে, মানে দ্বিমাত্রিক। কেন দ্বিমাত্রিক-ই হল? এইখানেই ওই আঞ্চলিকভাবে ইউক্লিডীয় স্থান জিনিসটার গুরুত্ব। গোলকের উপরিতল আঞ্চলিকভাবে ইউক্লিডীয়, অর্থাৎ এর যেকোন খুব ছোট্ট অংশ আসলে ইউক্লিডীয় স্থানের ছোট্ট অংশের মত দেখতে। কিন্তু কোন মাত্রার ইউক্লিডীয় স্থান? সহজেই বোঝা যায় যে গোলকের উপরিতলের খুব ছোট্ট অংশ আসলে দ্বিমাত্রিক ইউক্লিডীয় স্থানের ছোট অংশের মত দেখতে। আমরা পৃথিবীর ওপর দাঁড়িয়ে মাটিটাকে এইজন্যেই দ্বিমাত্রিক সমতলের মত দেখি, পৃথিবীপৃষ্ঠের তুলনায় আমার সেটার যে অংশ চোখে দেখতে পাই সেটা এতই ছোট যে আমরা সেটাকে সমতলই দেখি, পৃথিবীপৃষ্ঠের বক্রতা নজরে পড়ে না। আর এই খুব ছোট্ট অংশটা দ্বিমাত্রিক সমতলের ছোট্ট অংশের মত দেখতে বলেই স্পর্শক স্থানটা দ্বিমাত্রিক ইউক্লিডীয় স্থান। বৃত্তের পরিধির কথা ভাবা যাক।
পৃথিবীপৃষ্ঠের তুলনায় আমার সেটার যে অংশ চোখে দেখতে পাই সেটা এতই ছোট যে আমরা সেটাকে সমতলই দেখি, পৃথিবীপৃষ্ঠের বক্রতা নজরে পড়ে না। বৃত্তের ওপরে কোন বিন্দুতে স্পর্শক টানলে একটাই স্পর্শক রেখা আঁকা যাবে, ওই স্পর্শক রেখাটাই বৃত্তের ওপরের ওই বিন্দুতে স্পর্শক স্থান। বৃত্তের ছোট্ট একটা অংশ সুতোর টুকরোর মত, একমাত্রিক, তাই স্পর্শক স্থানটাও একমাত্রিক ইউক্লিডীয় স্থান।
পৃথিবীপৃষ্ঠের তুলনায় আমার সেটার যে অংশ চোখে দেখতে পাই সেটা এতই ছোট যে আমরা সেটাকে সমতলই দেখি, পৃথিবীপৃষ্ঠের বক্রতা নজরে পড়ে না।
সবকটা স্পর্শক মিলে একসাথে কেন একটা লিনিয়ার স্থান গঠন করবে সেটা অবশ্য বলিনি, কিন্তু ওপরের যুক্তিটা যদি আপনাদের বোঝাতে পেরে থাকি, তাহলে সেটা সহজেই বোঝা যায়। যে সমস্ত বস্তুর ওপর আমরা জ্যামিতি করব তারা সবাই আঞ্চলিকভাবে ইউক্লিডীয় স্থান, আর তাই তাদের খুব ছোট্ট অংশ কোন একটা মাত্রার ইউক্লিডীয় স্থানের মত দেখতে। স্পর্শক স্থানটা ঠিক সেই মাত্রার ইউক্লিডীয় স্থানের মতই দেখতে, একটু হেলানো। ইউক্লিডীয় স্থান যেহেতু লিনিয়ার স্থান,৯ তাই স্পর্শক স্থানটাও তাই হতে বাধ্য। এটা অঙ্ক কষে অনেক নিশ্চিত আর পরিষ্কারভাবে প্রমাণ করা যায় অবশ্যই, কিন্তু এক্ষেত্রে আমরা আঁক কষব না, শুধু ধারণাগুলো বোঝার চেষ্টা করব।
যাই হোক, ব্যাপারটা যা দাঁড়ালো তা হল ইউক্লিডীয় স্থানে যেমন প্রতিটি বিন্দুতে একটা লিনিয়ার স্থান আছে বলে ভাবতে পারি, ঠিক তেমনি আঞ্চলিকভাবে ইউক্লিডীয় স্থানেও প্রতিটি বিন্দুতে একটা লিনিয়ার স্থান আছে, ওই বিন্দুতে স্পর্শক স্থানটা। একটা জ্যামিতিক বস্তুর প্রত্যেকটা বিন্দুতে স্পর্শক স্থানগুলোকে একসাথে ভাবলে সেটাকে বলা হয় ‘স্পর্শক-গুচ্ছ’ বা ট্যানজেন্ট বান্ডল ( tangent bundle )। অঙ্কে এইরকম একগোছা স্থানের একটা মজার নাম আছে।
খড়ের গোছা
অঙ্কে এইরকম একগোছা স্থানকে বলে ‘তন্তু-গুচ্ছ’ বা ফাইবার বান্ডল (fiber bundle)। ব্যাপারটা মাটির ওপরে খাড়াভাবে ধরে রাখা খড়ের গোছার মত। জমিটা একটা স্পেস, আর সেই জমির ওপরে প্রতিটি বিন্দুতে একটা করে স্পেস, মানে খড়গুলো। কিন্তু খড়গুলো সবকটাই খড়, মানে একরকমভাবে সেগুলো একই জিনিস, শুধু এক একটা খড় হয়ত এক এক রকম ভাবে বেঁকে আছে। তন্তুগুচ্ছও ঠিক তাইই, একটা স্থান B, যাকে জমি-স্থান বা বেস স্পেস (base space) বলে, আর আর একটা স্থান F, যাকে তন্তু-স্থান বা ফাইবার স্পেস (fiber space) বলা হয়। আর জমি-স্থানের প্রতিটি বিন্দুতে তন্তু-স্থানের একটা করে কপি আছে, সেই কপিটাকে ওই বিন্দুর ওপরের তন্তু বা ফাইবার (fiber) বলা হয়। তন্তু-স্থান বা ফাইবার স্পেসটা একটাই, যদিও তন্তু বা ফাইবার অনেকগুলো, জমি-স্থানের প্রতিটি বিন্দুতে একটা করে।
এই ফাইবাররা সবাই ফাইবার স্পেসের কপি বটে, কিন্তু এরা একদম এক এরকম কিন্তু নয়। একটু টেরা-বাঁকা, হেলে পড়া এইসব আছে। আমরা ব্যাপারটাকে বাজে বাঁধাই করার মত ভাবতে পারি। ভাবা যাক একটাই পাতার অনেকগুলো ফটোকপি করে কেউ সেগুলোকে একসাথে নিয়ে একদিকটা বাঁধাই করে দিয়েছে। বাঁধাইটা যত্ন নিয়ে করা হলে পাতাগুলো একটার পর একটা সুন্দরভাবে থাকবে, আবার অগোছালোভাবে করা হলে সেইটা হবে না।
এই বেঁকা-টেরা ব্যাপারটা থেকে কি বোঝা যায়?
জ্যামিতিটা!!!
কিভাবে সেটা আবছাভাবে বুঝতে নিচে একটা ছবি দেওয়া যাক, এটাও একটা তন্তুগুচ্ছের ছবি, তবে স্পর্শক গুচ্ছ নয়, এটাকে বলে ‘উল্লম্ব-গুচ্ছ’ বা নরমাল বান্ডল ( normal bundle)। একটা সরলরেখার উপরে আর একটা বৃত্তাংশের উপরে উল্লম্ব গুচ্ছের ছবি।
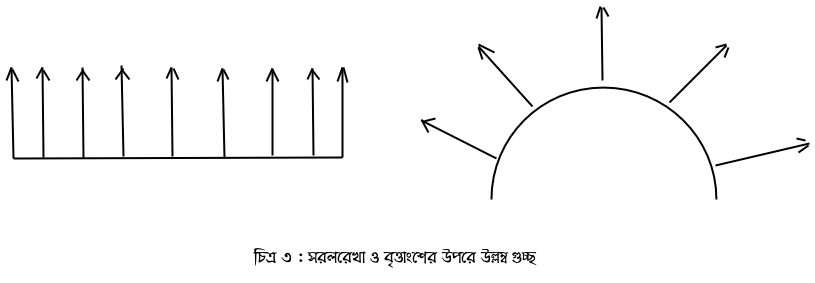
ছবিটা দেখে কি বোঝা গেল? সরলরেখার উপরে উল্লম্ব গুচ্ছটা ভালো বাঁধাই এর মত, আর বৃত্তাংশের উপরে উলম্ব গুচ্ছটা মোটেই সেরকম নয়, খড়গুলো একে অপরের ওপর হেলে পড়েছে যেন। নিচের জমি-স্থানটা কেমন দেখতে আমরা না জানলেও এই হেলে পড়াটা দেখে বলতে পারতাম সেটা সোজা বা চ্যাটালো নয়, বাঁকা। দ্বিসমতলের উপরে উল্লম্ব গুচ্ছ আর গোলকের উপরিতলের উপর উল্লম্ব গুচ্ছটাও এরকমই দেখতে হবে।১০
তন্তুগুচ্ছের তন্তু-স্থানটা যদি লিনিয়ার স্থান হয়, তাহলে সেরকম তন্তুগুচ্ছকে লিনিয়ার গুচ্ছ বা ভেক্টর গুচ্ছ ( linear bundle১১ বা vector bundle ) বলা হয়। স্পর্শক গুচ্ছ, উল্লম্ব গুচ্ছ সবই লিনিয়ার গুচ্ছের উদাহরণ।
কিন্তু জমি-স্থানের বক্রতা যেমন দেখতে নাও পেতে পারি আমরা, তেমনি কোন একটা লিনিয়ার গুচ্ছেরও তন্তুগুলোর হেলে পড়া যদি দেখতে না পাই? অন্যভাবে এই হেলে পড়াটা বুঝতে পারা উচিৎ। আসলে গাউস১২-এর সময় থেকেই জ্যামিতিকে ক্রমশই আরও বেশী করে জ্যামিতিক বস্তুটার আভ্যন্তরীণ ধর্ম১৩ হিসেবে ভাবা শুরু হয়, আজ অবধি সেই ভাবনার জয়যাত্রা অব্যাহত। মানে কি এর? মানে যে জিনিসটার জ্যামিতি নিয়ে ভাবছি সেই জিনিসটার বাইরে কি আছে সেইটা ভাবব না, সেই জিনিসটার বাইরে দাঁড়িয়ে সেই জিনিসটাকে দেখতে পাওয়ার সম্ভাবনাটাকে আমল দেব না। কেন? প্রথমত, পৃথিবীতে আমরা নিজেরা সেই অবস্থায় আছি বলে।
জ্যামিতিকে ক্রমশই আরও বেশী করে জ্যামিতিক বস্তুটার আভ্যন্তরীণ ধর্ম হিসেবে ভাবা শুরু হয়, আজ অবধি সেই ভাবনার জয়যাত্রা অব্যাহত। মহাশূন্যে পাড়ি না দিলে কিম্বা কৃত্রিম উপগ্রহ থেকে ছবি না তুললে পৃথিবীপৃষ্ঠের উপর থেকে পৃথিবীকে দেখার সুযোগ আমাদের নেই। দ্বিতীয়ত, আমরা ত্রিমাত্রিক জীব, বাইরে থেকে কিছু আমরা শুধু ত্রিমাত্রিক স্থানেই দেখতে পাই। তাই এই সম্ভাবনা বাদ রেখে জ্যামিতি করতে না শিখলে চার বা বেশী মাত্রার জ্যামিতি করার আশা একেবারে ছেড়ে দিতে হয়। অপেক্ষবাদে এই মহাবিশ্বের স্থান-কাল চারমাত্রার জিনিস। আর মহাবিশ্বের বাইরে কি আছে আমরা আদৌ জানি না। তাই স্থান-কালের জ্যামিতির সাথে এই মহাবিশ্বের পদার্থবিদ্যার সূত্রগুলোর সম্পর্ক বার করতে গেলে১৪ আমাদের জ্যামিতিকে এইভাবে গড়ে তোলা ছাড়া অন্য উপায় নেই।
জ্যামিতিকে ক্রমশই আরও বেশী করে জ্যামিতিক বস্তুটার আভ্যন্তরীণ ধর্ম হিসেবে ভাবা শুরু হয়, আজ অবধি সেই ভাবনার জয়যাত্রা অব্যাহত।
তাহলে এখন বাইরে থেকে হেলে পড়া দেখতে না পেলেও হেলে পড়া বুঝবো কিকরে? সেইজন্যেই ইউক্লিডীয় অ্যাফাইন স্থানের আলোচনায় মিলিয়ে দেওয়ার কথাটা বলেছিলাম। আমরা যদি একটা বিন্দুর ওপরের তন্তুকে আর একটা বিন্দুর ওপরের তন্তুর সাথে মিলিয়ে দেওয়ার চেষ্টা করি, তাহলে তন্তুগুলো ওই সরলরেখার উল্লম্ব গুচ্ছের মত সমান্তরাল হলে শুধু টেনে একই জায়গায় আনলেই হবে, আর হেলে পড়ে থাকলে টেনে একই জায়গায় আনার পরও মিলিয়ে দেওয়ার জন্য তাদের হেলাতে হবে। অর্থাৎ এই মিলিয়ে দেওয়ার পদ্ধতিটাতেও জ্যামিতিটা লুকিয়ে থাকবে। কিন্তু কি ঠিক মিলিয়ে দিতে চাইছি আমরা? ইউক্লিডীয় স্থানের ক্ষেত্রে সবগুলোই নেহাতই একই স্থানের টেনে আনা কপি, প্রত্যেক বিন্দুতেই যদি সমান্তরাল অক্ষ বেছে নিয়ে থাকি। এক্ষেত্রেও কি তাই? কিন্তু এই ‘সমান্তরাল’ মানে কি? ইউক্লিডীয় স্থানে নিচের জমিটাও লিনিয়ার স্থান, তাই কোন একটা ট্যানজেন্ট ভেক্টরকে, মানে কোন একটা স্পর্শককে একটা বিন্দু থেকে আর একটা বিন্দুতে ‘সমান্তরাল’ ভাবে বয়ে নিয়ে যাওয়া ব্যাপারটা কি সেটার একটা মানে আছে, কারণ সেই ক্ষেত্রে শুধু স্পর্শকটার গোড়ার বিন্দুটা নয়, গোটা স্পর্শকটাই ওই জমির ইউক্লিডীয় স্থানেই শুয়ে আছে, তাই টেনে নিয়ে যাওয়াটা সমান্তরাল হল কিনা খুব সহজেই মিলিয়ে নিতে পারব, জমির ইউক্লিডীয় স্থানে সেটা সমান্তরাল থাকছে কিনা সব বিন্দুতে সেইটা দেখে। মাটিতে একটা রুলারকে শুইয়ে সেটাকে মাটির ওপর দিয়ে টেনে নিয়ে যান এমনভাবে যাতে সবসময় রুলারটা প্রথমে যেমন ছিল তার সমান্তরাল থাকে, তাহলেই বুঝবেন এইটায় কোন জটিলতা নেই। কিন্তু নিচের জমি-স্থানটা বাঁকা হলে একটা স্পর্শক আদৌ আর জমি-স্থানের মধ্যে নাই থাকতে পারে। গোলকের উপরিতলের উদাহরণেই সেটা দেখতে পাবেন, যেকোন স্পর্শকই গোলকের উপরিতল ছেড়ে বেরিয়ে এসেছে। তাহলে এইক্ষেত্রে সমান্তরাল করে টেনে নিয়ে যাওয়া কথাটার একটা মানে দিতে হবে আমাদের। সেইটাকেই অঙ্কে বলে সমান্তরাল পরিবহন বা প্যারালাল ট্রান্সপোর্ট ( parallel transport) । এর পরের পর্বে আমরা দেখব যে কিভাবে সমান্তরাল পরিবহনের একটা মানে আমরা দিতে পারি আর কিভাবে সেই মানে দেওয়াটার সাথে তৃতীয় ধাপের সমস্যাটা, মানে ইনার প্রডাক্ট বসিয়ে দূরত্ব ও কোণ মাপার সমস্যাটা জড়িয়ে।
(চলবে)
১রীমান এর আগেও এইটা জানা ছিল… রীমানের কৃতিত্ব এক্ষেত্রে এই যে তিনি বুঝলেন জ্যামিতি করতে এই ধর্মটা লাগবেই।
২Locally euclidean কথাটার মধ্যেই লুকিয়ে আছে যে এরা topological space, locally euclidean topological space. আরো কিছু টেকনিকাল শর্তও আছে, এদেরকে second countable ও Hausdorff topological space হতে হবে, কিন্তু সেসব কচকচি আপাতত থাক।
৩দ্রাঘিমারেখাদের সমান্তরাল করে না আঁকলেও সম্ভব নয় আসলে। এইটা ধ্রুপদী অবকলন জ্যামিতির ( classical differential geometry ) একটা উপপাদ্য। গাউস ( Carl Friedrich Gauss ) উপপাদ্যটা আবিষ্কার করে এতই আশ্চর্য হয়েছিলেন যে তিনি উপপাদ্যটার ল্যাটিন নাম রাখেন Theorema Egregium, ‘remarkable theorem’, ‘চমকপ্রদ উপপাদ্য। ‘ গাউস এই উপপাদ্যে প্রমাণ করেন যে যদি দুটো তলের (surface) মধ্যে যদি যথেষ্ট ‘মসৃণ’ (smooth) এমন কোন অপেক্ষক ( mapping বা function) থাকে যা একটা বস্তুর প্রতিটি বিন্দুকে অন্যটায় নিয়ে যায় আর যেকোন দুটো কাছাকাছি বিন্দুর মধ্যে দূরত্ব একই রাখে ( এই শর্তটা পূরণ হলে ঐরকম অপেক্ষককে local isometry বলা হয়), তাহলে ঐ দুই তলের গাউসীয় বক্রতা ( Gaussian curvature, বক্রতার একধরণের পরিমাপ) এক হতে বাধ্য। যেহেতু কাগজের গাউসীয় বক্রতা শূন্য আর গোলকের উপরিতলের গাউসীয বক্রতা 1/R, যেখানে R গোলকের ব্যাসার্ধ, তাই পৃথিবীর সঠিক মানচিত্র কাগজে আঁকা অসম্ভব !!
৪এইভাবে গোলকের উপরে পাওয়া স্থানাঙ্ককে বলে cartographic coordinates বা geographic coordinates, ভৌগোলিক স্থানাঙ্ক, এতে দুই মেরু বাদ পড়ে। একটা বিন্দু মাত্র ( যেকোন একটা মেরু ) বাদ পড়বে এমন স্থানাঙ্কও হয়, stereographic coordinates বলে। কিন্তু একটাও বিন্দু বাদ পড়বে না এমন স্থানাঙ্ক সম্ভব না।
৫এই তফাতটা স্পষ্ট করতে অনেক সময় অঙ্কে ‘free vector’, এই পরিভাষা ব্যবহার হয়। free vector মানে যে ভেক্টরের শুরুর বিন্দু আর অন্তিম বিন্দু কোনটাই বলা নেই, শুধু দৈর্ঘ্য আর দিক বলা আছে। ওই AB ভেক্টরের সমান দৈর্ঘ্যের সমান্তরাল যেকোন ভেক্টরই পদার্থবিদ্যায় AB ভেক্টরের সমান ( যদিও ভ্রামক হিসেব করার সময় নয়), কিন্তু অঙ্কে একমাত্র এইগুলোর মধ্যে যেটা মূলবিন্দুতে শুরু হচ্ছে সেইটাই ‘ভেক্টর’, অন্যগুলো নয়।
৬A tangent is a line that kisses the curve once and misses it for ever.
৭কোণা থাকলে আর সেটা নাও হতে পারে। ইংরাজি V হরফটার কথা ভাবুন। V এর সবচেয়ে নিচের বিন্দুটায় স্পর্শক টানার চেষ্টা করলেই বুঝবেন যে বিন্দুটা ডানদিক থেকে এসেছে ভাবলে স্পর্শকটা ডানদিকের বাহু বরাবর রেখাটা, আর বাঁদিক থেকে এসেছে ভাবলে বাঁদিকের বাহু বরাবর রেখাটা স্পর্শক।
৮সাধারণ অর্থে সরলরেখা, মানে সত্যিই সোজা রেখা।
৯স্পর্শক স্থানের ক্ষেত্রে আর ওই গণ্ডগোলটা নেই যে যেকোন বিন্দুকেই মূলবিন্দু ধরা যায়। কারণ এক্ষেত্রে একটা সুনির্দিষ্ট মূলবিন্দু আছে। সেটা হচ্ছে যে বিন্দুটায় স্পর্শক স্থানটা জ্যামিতিক বস্তুটাকে স্পর্শ করেছে। গোটা স্পর্শক স্থানটায় ওই একটামাত্র বিন্দুই আমরা যে জ্যামিতিক বস্তুটা নিয়ে স্পর্শক স্থান আঁকতে শুরু করেছিলাম নিশ্চিতভাবেই সেই বস্তুটার ওপর আছে, তাই কোন একটা বিন্দুতে স্পর্শক স্থান একটা লিনিয়ার স্পেস, যার মূলবিন্দু ওই বিন্দুটাই।
১০বস্তুত মাটিতে খাড়া একটা কাঠি পুঁতে বিভিন্ন সময়ে তার ছায়ার দৈর্ঘ্য মেপে সেই জায়গার অক্ষাংশ বার করা যায় এই উলম্বগুচ্ছের হেলে পড়ার জন্যই।
১১Line bundle নয় কিন্তু, যদিও line bundle ও একরকম vector bundle, কিন্তু একটা বিশেষ ধরণের vector bundle।
১২Carl Friedrich Gauss
১৩Intrinsic property, এইভাবে জ্যামিতিকে ভাবা হলে সেইটাকে intrinsic geometry ও বলা হয়ে থাকে। intrinsic মানে আভ্যন্তরীণ, যা কিছু কোন একটা জিনিসের ভিতরকার, বাইরের কিছুর ওপর নির্ভরশীল নয়।
১৪সাধারণ অপেক্ষবাদ বা general relativity তে ঠিক তাইই করা হয়।