প্রথমেই বলে দি যে বিন্দু ভর বা চার্জের ধারণা আসলে একটা গাণিতিক ধারণা, যা বাস্তব জগতে কখনো মোটামুটিভাবে, ইংরেজীতে যাকে বলে approximately, খেটে যায়। যেহেতু এটা একটা approximation, তাই আমরা সবসময় এই ধারণা ব্যবহার করতে পারি না এবং এই ব্যাপারটা আমাদেরকে স্কুলে বলাও হয় না। তাই তোমার প্রশ্ন খুবই প্রাসঙ্গিক।

বিশদে উত্তর দেওয়ার আগে একটা উদাহরণ দিই। ধর, তোমার কাছে একটা সাদা রঙের ফুটবল আছে। ফুটবলটাকে একটা চেয়ারে রাখো। এবার ফুটবলটার একদম কাছে, এই ধর এক হাত দূরত্বে গিয়ে বলটাকে দেখার চেষ্টা কর। দেখবে বলটা বেশ গোলগোল দেখতে লাগছে, আর তুমি বুঝতে পারছ ওটা একটা বল। তুমি দেখতে পাচ্ছ বলটা সাদা রঙের ষড়ভুজাকার  আর পঞ্চভুজাকার  অংশ দিয়ে বানানো, আর ওই অংশগুলোর ফাঁকে ফাঁকে আবার সেলাই করা আছে, মানে তুমি বলের পুরো আকারটা দেখতে পাচ্ছ। এবার ধর তুমি প্রায় ১০ মিটার দুরে চলে গেলে। দেখবে তুমি ওই ষড়ভুজাকার আর পঞ্চভুজাকার অংশগুলো দেখতে পাচ্ছ, কিন্তু তুমি আর সেলাইগুলো ভাল করে দেখতে পাচ্ছ না। এবার আরও দুরে চলে যাও। ধর তুমি একটা গোলপোস্টে বলটাকে রেখে অন্য গোলপোস্টে গিয়ে বলটাকে দেখছ। কি দেখবে? যে ওই ষড়ভুজাকার আর পঞ্চভুজাকার অংশগুলো আর তুমি দেখতে পাচ্ছ না, খালি বলটা যে সাদা সেটা বুঝতে পারছ। আর বলটাও কিরকম সাইজে ছোট মনে হচ্ছে। এবার সম্ভব হলে তুমি আরও দূরে চলে যাও। দেখবে বলটাকে আর বল বলে মনে হচ্ছে না, একটা সাদা বিন্দুর মত লাগছে। অর্থাৎ, তুমি যত দূরে চলে যাচ্ছ, বলটার আকারের বৈশিষ্ট্যগুলো তত মুছে যাচ্ছে আর শেষমেষ ওটাকে কেবল একটা বিন্দু বলে মনে হচ্ছে।

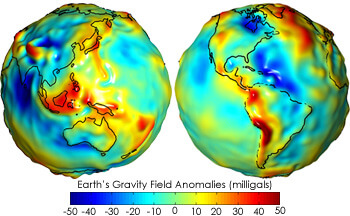
ঠিক একইরকম ব্যাপার হয় মহাকর্ষ বলের ক্ষেত্রে। যখন তুমি পৃথিবী বা অন্য কোনো গোলাকার বস্তুর খুব কাছে থাক, তখন পৃথিবীর এই গোলাকার ব্যাপারটা বোঝা যায়। শুধু তাই নয়, পৃথিবী যে ঠিক গোলাকার নয়, বরং এবরো-খেবড়ো সেটাও স্যাটেলাইট দিয়ে মহাকর্ষ বল মেপে বোঝা যায়। কৃত্রিম উপগ্রহ পাঠাতে বা ইন্টারন্যাশনাল স্পেস স্টেশনে রকেট পাঠাতে পৃথিবীর পুরো আকারটা জানা জরুরী। কিন্তু যখন তুমি পৃথিবী আর সূর্যের ভিতর মহাকর্ষ বল মাপতে যাবে, পৃথিবী আর সূর্য একে অপরের থেকে এতটাই দূরে যে দুজনকেই ফুটবলটার মত বৈশিষ্ট্যহীন একটা গোল বস্তু হিসেবে ভাবতে পারো। এবার তুমি একটা ছোট্ট গণনা করে দেখাতে পারো যে, যদি একটা গোলকের সব জায়গায় সমান ঘনত্ব থাকে তাহলে গোলকটার বাইরে যেকোনো বিন্দুতে মহাকর্ষ বলের মান এমন হয়, যেন গোলকটার সমস্ত ভর ওর কেন্দ্রবিন্দুতে বসে আছে। মানে তুমি যদি গোলকটাকে দেখতে না পাও, তাহলে গোলকটার বাইরে মহাকর্ষ বল মেপে বুঝতে পারবে না যে ওটা গোলক না একটা বিন্দু ভর। সেই কারণে, আমরা জ্যোতির্বিদ্যায় বেশিরভাগ সময়ই বিন্দু ভরের ধারণা ব্যবহার করতে পারি।

কিন্তু কত দূরে যেতে হবে বিন্দু ভরের ধারণা ব্যবহার করার জন্য? জিনিসটা অঙ্ক কষে বের করা যায়। বিন্দুভরের ধারণার সাথে আরেকটি ধারণা যুক্ত করে আমরা বাস্তব জগতের এবড়োখেবড়ো বস্তুর জন্য মহাকর্ষ বা কুলম্বের বল হিসেব করতে পারি। এই যে নতুন ধারণাটির কথা বলছি তার নাম হল সুপারপোজিশান, যাকে বাংলায় উপরিপাত নাম দেওয়া যেতে পারে।  অর্থাৎ দুটি এলোমেলো আকারের বস্তু ‘ক’ আর ‘খ’-এর মধ্যে বলের হিসেব করতে হলে তাদের অনেকগুলো ছোট ছোট ভাগে ভাগ কর, যেগুলোকে মোটামুটি বিন্দু হিসেবে ধরা যায়। তারপর, ‘ক’-এর সব কটা বিন্দু আর ‘খ’-এর সব কটা বিন্দুর মধ্যে কি বল কাজ করছে তা মহাকর্ষ বা কুলম্বের সূত্র লাগিয়ে জোড়ায় জোড়ায় বের কর। এবার এই সব বলকে যোগ কর।বুঝতেই পারছ কাজটা খুব একটা সহজ না-ই হতে পারে। কিছু বিশেষ ক্ষেত্রে ক্যালকুলাস বা কলনবিদ্যা লাগিয়ে অঙ্কটা কষে ফেলা যায়, কিন্তু বেশীর ভাগ ক্ষেত্রেই কম্প্যুটারের সাহায্য নিতে হবে।

তবে তুলনামূলক সহজ উপায়ে এই অঙ্কটা অনেক সময় কষা হয় multipole expansion বলে একটা পদ্ধতি ব্যবহার করে। এই পদ্ধতিতে তুমি যেকোনো আকৃতির একটা বস্তুকে বিন্দু ভর (monopole), একটা dipole, quadrupole, এইসব নানা আকারের সমষ্টি হিসেবে ভাবতে পার। এইসব আকারগুলোর জন্য মহাকর্ষ বল মাপা সোজা। আর যেহেতু মহাকর্ষ বল সুপারপোজিশানের নীতি মেনে চলে, তাই আমরা এই বিভিন্ন আকারের মাধ্যমে মাপা মহাকর্ষ বলগুলোকে ভেক্টর পদ্ধতিতে জুড়ে দিয়ে বস্তুটার মোট মহাকর্ষ বল মাপতে পারি। গণনা করে দেখানো যায় যে monopole মানে বিন্দু ভরের জন্য বস্তুটি যে বল প্রয়োগ করে তার মান দূরত্বের সাথে সাথে সবথেকে ধীরে ধীরে কমে। এরপর আসে dipole এর পালা, তারপর আসে quadrupole-এর পালা, তারপর octopole … এরকম ভাবেই যত pole-এর পরিমান বাড়তে থাকে বলের মান দূরত্বের সাথে তত তাড়াতাড়ি কমতে থাকে। এবার এই বিভিন্ন আকারগুলো থেকে বলগুলো কষে তুমি দেখাতে পারো যে কোনো প্রায় গোলাকার বস্তুর কেন্দ্র থেকে যদি তুমি মোটামুটি এক ব্যাস পরিমান দূরে চলে যাও, তাহলে শুধু বিন্দু ভর ব্যবহার করেই তুমি প্রায় সমস্ত গণনা করতে পারবে।

বিশদে জানতেঃ

Multipole expansion কিভাবে ব্যবহার করা হয় তা জানতে উইকিপিডিয়ার এই লেখাটি দেখতে পার।