৩ নম্বর স্বতঃসিদ্ধ বলছে – একটি বিন্দু ও একটি দূরত্ব দেওয়া থাকলে ওই বিন্দুকে কেন্দ্র করে ওই দূরত্বের সমান ব্যাসার্ধের বৃত্ত আঁকা যায়। এখানে যা বলা হল সেটা বুঝতে এমনিতে কোন অসুবিধে নেই| কিন্তু ঠিক সেইজন্যেই এখানে যে আদৌ কিছু একটা ‘দেওয়া হল’ সেটা খেয়াল করা একটু মুশকিল। এখানে আসলে যেটা দেওয়া হল সেটা হল একটা স্কেল বা রুলার! মানে দূরত্ব মাপার একটা কিছু।
৪ নম্বর স্বতঃসিদ্ধ ভয়ানক গোলমেলে। এটা বলছে – সমস্ত সমকোণ পরস্পরের সমান। কিন্তু এর মানে কি? গোলমেলে ব্যাপারটায় যাচ্ছি, তবে তার আগে আরেকটা জিনিস খেয়াল করব| ৩ নম্বর স্বতঃসিদ্ধ যেমন দূরত্ম মাপার একটা কিছু দেয়, এখানে কোণ মাপার কিছু একটা লাগবে আমাদের। কিন্তু তাও বাকিটা পরিষ্কার নয়। সেটা পরিষ্কার করতে আমরা প্রথমে সমকোণের সংজ্ঞা খুঁজব| সেটা হলো এইরকম:
‘দুইটি সরলরেখা পরস্পরকে লম্বভাবে ছেদ করলে তাদের মধ্যবর্তী কোণ এক সমকোণ।’
এইবার বোধহয় খানিক পরিষ্কার হল ব্যাপারটা, তাই না? মানে ৪ নম্বর আসলে বলছে – যেকোনো দুইটি সরলরেখা পরস্পরকে লম্বভাবে ছেদ করলে তাদের উৎপন্ন কোণ সমান।
এখানে মনে হতে পারে যে আমরা একটা শব্দের বদলে আর একটা শব্দ বসালাম যার একই মানে। লম্বভাবে ছেদ করা কথাটার মানে কি? এর উত্তরে বলা যেতে পারে: দুটি সরলরেখা যখন পরস্পরকে ছেদ করে ও তাদের উৎপন্ন কোণের মান এক সমকোণ হয়, তখন ওই দুই সরলরেখাকে পরস্পরের উপর লম্ব (বা পরস্পরকে লম্বভাবে ছেদ করেছে) বলা হয়| তবে এই উত্তর দিলে আমাদের যুক্তিটা শুধুই গোল গোল ঘুরতে থাকবে। ‘লম্বভাবে ছেদ করা’ ব্যাপারটাকে অন্যভাবে বলতে হবে।
এই ফাঁকে সংজ্ঞা নিয়েও খানিক আলোচনা করে নেওয়া যাক। এতক্ষণ অবধি কোন সংজ্ঞা না বলেই আমরা কাজ চালাচ্ছিলাম। তার কারণ হলো – ইউক্লিডের এলিমেন্টস এ সংজ্ঞা আছে প্রথমেই, কিন্তু সারা বইতে কোথাও সেই সংজ্ঞাগুলোর কথা আর কখনো সেভাবে আসেনি।১ তাছাড়া বেশিরভাগ সংজ্ঞাই খুব গোলমেলে, যেভাবে সংজ্ঞা দেওয়া হয়েছে সেইভাবেই বাকি বইতে সবসময় ব্যবহার হয়েছে তাও নয়।
আর একটা ব্যাপার হল, সংজ্ঞারা কিন্তু জ্যামিতিতে দেওয়া থাকা জিনিসগুলোর মধ্যে নয় ঠিক। ভালো সংজ্ঞা তৈরী করতে হলে, কোন জিনিসগুলো আগে সংজ্ঞায়িত করব, আর কোনগুলোর জন্য আগে সংজ্ঞায়িত জিনিসগুলোর সাহায্য নেব, এ বিষয়ে সিদ্ধান্ত খুবই জরুরী। কাজের অনেক সুবিধে হয় তাতে, বুঝতেও। অবশ্য জ্যামিতির অনেক জিনিসেরই নিখুঁত সংজ্ঞা দেওয়া সম্ভব না। যেমন বিন্দু। বিন্দুর এমন কোন সংজ্ঞা দেওয়া সম্ভবই না যেটা থেকে বিন্দু কি এইটা কোন গোলমাল ছাড়া বোঝা যাবে। অথচ বিন্দু কি সে তো আমরা জানি একরকম। এই একরকম জানি অথচ সংজ্ঞা দেওয়া যায় না, এমন জিনিসগুলোকে অঙ্কে বলা হয় primitives বা primitive notions| আমরা বলব অসংজ্ঞায়িত প্রাথমিক ধারণা।২
তা মোদ্দা কথাটা হল যে সংজ্ঞাই হোক কি অসংজ্ঞায়িত প্রাথমিক ধারণাই হোক, এগুলো জ্যামিতিতে দেওয়া থাকা জিনিস নয়, এগুলো আমরা বেছে নিতে পারি। হিলবার্ট ১৮৯৯ সালে৩ জ্যামিতিকে অন্যভাবে সাজালেন । এই প্রসঙ্গেই হিলবার্টের মন্তব্য – “আমরা বিন্দু, সরলরেখার জায়গায় চেয়ার, টেবিল, বীয়ারের মগ এইসব দিয়েও জ্যামিতি শুরু করতে পারতাম।” এর অর্থ হলো: কি দিয়ে শুরু করব তা সুবিধার জন্যে খুব জরুরী জিনিস, কিন্তু নীতিগতভাবে জরুরী নয়।
কিন্তু, স্বতঃসিদ্ধগুলো এই অসংজ্ঞায়িত প্রাথমিক ধারণাগুলোর মধ্যে আন্তঃসম্পর্ক| অর্থাৎ, সেগুলো একদমই দেওয়া থাকা জিনিস| সেগুলো আলাদা হলে যে জ্যামিতি আমরা পাব তা বেশ আলাদা হবে, ভীষণভাবেই আলাদা।৪
যাই হোক, ১,২, ৩ আর ৪ নম্বর স্বতঃসিদ্ধ কি বলছে আমরা দেখলাম। এও দেখলাম সংজ্ঞা ব্যাপারটা জ্যামিতিতে ভারী গোলমেলে। কিন্তু সংজ্ঞা না দিই, কাজ চালানো গোছের কিছু একটা তো বলতে হয়। সেটা আমরা বলব, কিন্তু তার আগে আমাদের অন্য একটা জিনিস একটু বুঝে নিতে হবে। অঙ্কে এটা একটা খুবই গুরুত্বপূর্ণ পদক্ষেপ- জ্যামিতির বীজগাণিতিকরণ। ঘাবড়ে যাওয়ার কিচ্ছু নেই, জিনিসটা আমাদের বেশ পরিচিত – স্থানাঙ্ক জ্যামিতি (coordinate geometry)। আর একটুখানি ভেক্টর বীজগণিত।
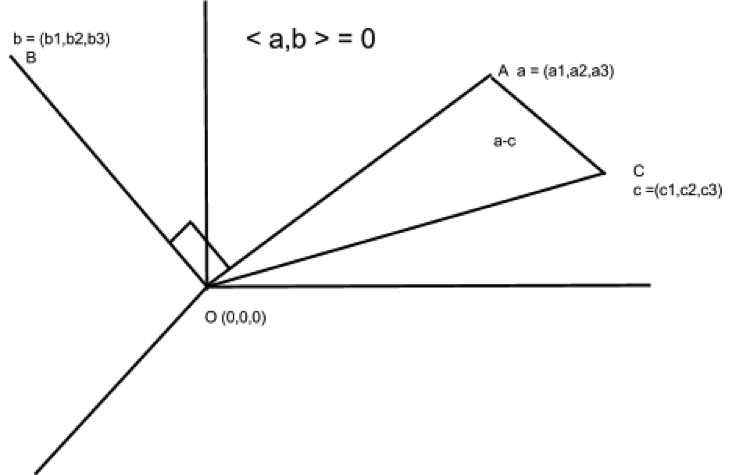
বোঝার সুবিধের জন্য ধরুন, আমরা আছি 
এইটাই আমাদের ৩ নম্বর স্বতঃসিদ্ধের আলোচনায় বলা স্কেল| এর নাম ইউক্লিডিয়ান দূরত্ব অপেক্ষক (euclidean distance function)। এর বেশ কিছু মজার প্রপার্টি আছে:
-
, আর
একমাত্র তখনই হবে যদি
হয়।
-
-
, এইটার নাম ত্রিভুজ অসমতা বা triangle inequality.৫
স্থানাঙ্ক জ্যামিতির ভাষায় স্কেল কি, তা আমরা বুঝলাম। কিন্তু চাঁদা? আমাদের অনেকেরই মনে পড়বে ফিজিক্সে পড়া ডট প্রডাক্টের কথা।
a আর b এই দুই ভেক্টরের ডট প্রডাক্ট বা স্কেলার প্রডাক্ট বা ইনার প্রডাক্ট (inner product) হল:
a ও b এর পরস্পরের লম্ব হওয়া (যার মানে OA আর OB সরলরেখাদ্বয়ের পরস্পরের লম্ব হওয়া) আর 
দ্বিতীয় সমতাটিকে শুধু লেখার সুবিধার্থে করা নামকরণ ভাবতে পারেন| অথবা ভাবতে পারেন,ওটা a ভেক্টরের দৈর্ঘ্য বা মান| অঙ্কের ভাষায় যাকে বলে a এর নর্ম (norm of a)।, যেখানে
ওই দুই ভেক্টরের মধ্যে উৎপন্ন কোণ।
এই শেষেরটা খুব জরুরী, কারণ ওইটা বলছে কোণ মাপার চাঁদাটা দিয়ে দিলেই দূরত্ম মাপার স্কেলটাও পেয়ে যেতাম। তার আগেরটা অবশ্যই বলছে যে এই চাঁদাটা পুরোদস্তুর চাঁদা, যেকোনো কোণই মাপতে পারে, শুধু সমকোণ নয়।
তাহলে এখনো অবধি কি দাঁড়ালো? ইউক্লিডের প্রথম ৪ টে স্বতঃসিদ্ধ আমাদের দিল ইউক্লিডিয়ান স্পেস আর এই ইনার প্রডাক্টটা? ঠিক তাই !!
বিশ্বাস না হলে কষে দেখতে পারেন: দ্বিমাত্রিক ইউক্লিডীয় সমতলে, মানে 
পরের অংশে আমরা যাব সবচেয়ে ধাঁধালো স্বতঃসিদ্ধটায়।
প্রচ্ছদের ছবি : উইকিপিডিয়া
.svg){kind=link}
১বইয়ের প্রথমে ওই সংজ্ঞাগুলো সে কারণে অনেকেই মনে করেন যে ইউক্লিডের নিজের দেওয়া নয়, হেরন নামে আর একজন গণিতজ্ঞ বা তার কোন ছাত্রছাত্রী পরে এলিমেন্টস এ ওইগুলো জুড়ে দেন, তবে এ মত বিতর্কিত।
২১৮৮২ সালে প্রকাশিত হয় পাশ ( Moritz Pasch ) এর বই Vorlesungen über neuere Geometrie( বইয়ের নামের ইংরাজি তর্জমা lectures on modern geometry )। পাশ এই বইতে ইউক্লিডের জ্যামিতিকে সঠিক যৌক্তিক ভিত্তির ওপর দাঁড় করালেন, primitives এর ধারণাও ওনারই দেওয়া। এই বইটির প্রভাব কত ব্যাপক আজকের ম্যাথেমেটিক্সে সেটা বোধহয় শুধু এইটুকু বললেই বোঝা যাবে যে এই বই পিয়ানোর ( Giuseppe Peano ) কাজকে প্রভাবিত করেছিল – শুধু জ্যামিতি নয়, গোটা অঙ্কশাস্ত্রের যৌক্তিক ভিত্তির দিকে প্রথম পদক্ষেপ এই বই।
৩১৮৯৯ সালে প্রকাশিত হিলবার্টের ( David Hilbert ) বই grundlagen der geometrie ( বইয়ের নামের ইংরাজি তর্জমা foundations of geometry ) অত্যন্ত সুদূরপ্রসারী প্রভাব ফেলা সাড়াজাগানো একটি বই।
৪হিলবার্টের grundlagen der geometrie বই তে হিলবার্ট এই স্বতঃসিদ্ধগুলোকেও ঢেলে সাজিয়েছিলেন, এবং আরও অনেকেই এ কাজ করেছেন প্রায় কাছাকাছি বা পরবর্তী সময়ে, যেমন Mario Pieri, G.D. Birkhoff, Oswald Veblen, Alfred Tarski এবং আরো অনেকে। কিন্তু এই কাজগুলো সবই ইউক্লিডের জ্যামিতি বা তার অংশবিশেষ পাওয়ার জন্যে লেখা axiomatic system. আলাদা স্বতঃসিদ্ধ হলে আলাদা জ্যামিতির আলোচনায় আমরা ফিরে আসব।
৫এইটা Elements এ একটা উপপাদ্য আসলে: ত্রিভুজের দুটি বাহুর যোগফল তৃতীয় বাহু অপেক্ষা বৃহত্তর।