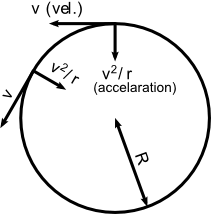
এর পর আসা যাক বৃত্তের উপর সমান গতিতে চলার বিশ্লেষণে। গতির মান অপরিবর্তিত থাকলেও তার দিশা সমানে বদলাচ্ছে – এর ফলে তার রয়েছে ত্বরণ (acceleration)। এই ত্বরণ এর মান (
গতিবেগের (velocity) মান ও
বৃত্তের ব্যাসার্ধ) এবং তার দিক বৃত্তের কেন্দ্রবিন্দুর (center এর) দিকে। এই ত্বরণকে বলে centripetal acceleration এর প্রমাণ জ্যামিতির (geometry) সাহায্যে করা যায় acceleration =
মাথায় রেখে।
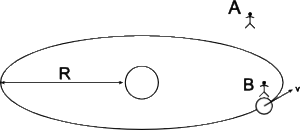
উদাহরণ স্বরূপ নেওয়া যায় পৃথিবীর সূর্যকে প্রদক্ষিণ করার ব্যাপারটা (Fig. 7)। বাইরে অবিস্থিত পর্যবেক্ষক (Observer) A দেখবে পৃথিবীর গতিবেগ (velocity) এবং তরণ (acceleartion)
. Newton-এর দ্বিতীয় সূত্র (second law) হিসেবে সে লিখবে (radius বা ব্যাসার্ধ বরাবর),
যেখানে হচ্ছে সেই বল যা দিয়ে সূর্য পৃথিবীকে টানছে (এই বল Newton এর gravitational attraction (মহাকর্ষ বল) যা কিনা যে কোনো দুটি বস্তুর মধ্যে বিদ্যমান। বস্তু দুটি যদি গোলাকার (spherical) হয় এবং তাদের ভর যদি হয় m1 এবং m2 আর গোলক (Sphere)-দুটির কেন্দ্রবিন্দুর মধ্যে দূরত্ব হয় R, তাহলে এই বলটির মান
এবং তার দিশা যে সরলরেখা কেন্দ্রবিন্দুদুটির মধ্যে দিয়ে গেছে সেই সরলরেখা বরাবর। একটি গোলক অন্যটিকে আকর্ষণ করে । G কে বলে Gravitational constant বা মহাকর্ষীয় ধ্রুবক । এখানে উল্লেখযোগ্য যে মধ্যাকর্ষণ বলের সমীকরণে যে mass (ভর) আসে তাকে বলে gravitational mass বা মহাকর্ষীয় ভর । এর আগে আমরা দেখেছি inertial mass । এটা অত্যন্ত আশ্চর্যের যে inertial mass এবং gravitational mass সমান।
এইবার দেখা যাক পর্যবেক্ষক B কি বলবে। B দেখছে পৃথিবী স্থির। সে একজন non inertial observer (rotating observer)। সে পৃথিবীর উপর দুটি বল আছে মনে করবে - একটি Newton-এর gravitational force যেটি সূর্যের দিকে , অন্যটি আমাদের Eq.(2) এর pseudo force। এইবার
এবং সূর্যের দিকে - তাই pseudo force টি
এবং বাইরের দিকে। Observer B বলবে,
কারণ পৃথিবী তার কাছে স্থির। পর্যবেক্ষক A এবং পর্যবেক্ষক B -এর সিদ্ধান্ত (conclusion) এক : কিন্তু তাদের বিশ্লেষণ আলাদা।
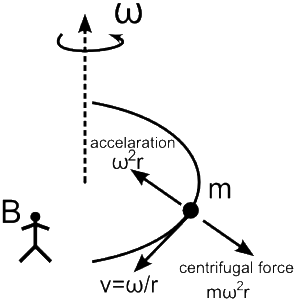
বৃত্তের উপর ধ্রুবগতিতে চলমান Observer-এর গতিবেগের মান যদি হয় এবং বৃত্তের ব্যাসার্ধ যদি হয় R তাহলে এই non-inertial observer বলবে যে কোন ভর m-এর বস্তুর উপর একটি pseudo force রয়েছে যার মান
, যার দিক ব্যাসার্ধ বরাবর এবং কেন্দ্রবিন্দু থেকে বাইরের দিকে। এই বলকে বলা হয় centrifugal force, যার অস্তিত্ব কেবল non inertial frame-এ ঘূর্ণায়মান পর্যবেক্ষকের (Rotating observer) জন্য।
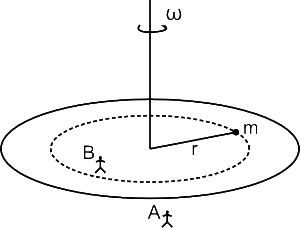
এবার কল্পনা করা যাক একটি rotating platform, merry-go-round-এ বা নাগরদোলায় যেরকম থাকে, গ্রামোফোনে যেরকম থাকতো বা microwave oven-এ যেরকম থাকে। Platform-টির ঘূর্ণনবেগ (rotational speed) ω এবং ঘোরার axis (অক্ষ)- টা vertical axis (Fig.8)। একজন পর্যবেক্ষক A দাঁড়িয়ে আছে platform-এর বাইরে , অন্যজন B platform-এর ওপর কেন্দ্রবিন্দু থেকে r দূরত্বে। একটি পাথর রয়েছে platform-এর ওপর। পাথরের ভর m, তার দূরত্বও কেন্দ্র থেকে r এবং পাথর ও platform-এর মধ্যে রয়েছে friction(ঘর্ষণ বল)।
Observer A (inertial): সে দেখছে পাথরটি প্ল্যাটফর্মের সঙ্গে ঘুরে যাচ্ছে। তাই পাথরের Speed (দ্রুতি) এবং পাথরটি r ব্যাসার্ধের বৃত্তের উপর এই constant speed-এ চলছে। অতএব তার ত্বরণ বৃত্তের কেন্দ্রের দিকে, ব্যাসার্ধ বরাবর, এবং তার মান
। এখানে বাহ্যিক বল (External force) কে? তা হল Friction
। নিউটনের দ্বিতীয় সূত্র এই Observer লিখবে এইভাবে,
Observer B (Rotating, non-inertial): B বলবে পাথরটি অচল। External Force রয়েছে- friction, বৃত্তের কেন্দ্রবিন্দুর দিকে (Eq. (15) দেখ)। এর সঙ্গে জুড়বে Pseudo force- এই ক্ষেত্রে Centrifugal force যা কিনা বহির্মুখী। সে নিউটনের সূত্র লিখবে,
একই উত্তর কিন্তু যুক্তি (argument) সম্পূর্ণ আলাদা।
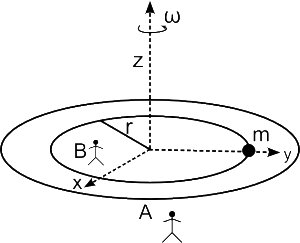
এবার ধরা যাক friction নেই। Rotating platform-টি পাথরের তলা দিয়ে নির্বিঘ্নে ঘুরে যাবে। পাথরের সঙ্গে তার কোন ঘষা লাগবে না। যে মুহূর্তে Platform ঘুরতে শুরু করল তখনকার অবস্থা Fig. 9-এ দেখানো হল। এখানে x,y,z অক্ষ দিয়ে তৈরী coordinate system আঁকা হল। Platform-টি z=0 তল(plane)-এ অবস্থিত। অর্থাৎ platform-টি x-y তলে রয়েছে। যে মুহূর্তে ঘূর্ণন শুরু হল তখন Observer B-এর position (r,0) এবং পাথরের position (0,r) [x-y তলে একটি বিন্দুর co-ordinate হল (x,y)]
Observer A: প্ল্যাটফর্ম ঘুরছে কিন্তু পাথর একজায়গায় দাঁড়িয়ে আছে- তার উপর কোন বাহ্যিক বল নেই, তার কোন ত্বরণ-ও নেই। B যে কিনা প্ল্যাটফর্মের সঙ্গে লাগা সে প্ল্যাটফর্মের সঙ্গে ঘুরবে এবং পাথরের সঙ্গে ধাক্কা খাবে সময় পরে। (m এবং B-এর মধ্যে কৌণিক দূরত্ব (angular distance)
, সেটা অতিক্রম করতে সময় লাগবে
)।
Observer B: নিজের গতি বোঝার উপায় নেই B-এর। সে দেখবে পাথর এসে তার সঙ্গে ধাক্কা খাচ্ছে সময় পরে। বিশ্লেষণ করতে হবে এটা কি করে সম্ভব। কোনো সত্যিকারের external force পাথরের ওপর নেই। B non inertial observer (rotating) — সে পাথরের ওপর pseudo force দেখবে। যে pseudo force-এর কথা আমরা শিখেছি সেটা হল centrifugal force। বৃত্তের ওপর চলমান পর্যবেক্ষকের জন্য এই বল ব্যাসার্ধ বরাবর বহির্মুখী ও তার মান mω2r । ভেক্টরের সঙ্কেতে (Vector notations)-এ লিখলে,
(আগের মতই ভেক্টর রাশিকে মোটা অক্ষরে লেখা হচ্ছে।)
এবং
, x এবং y-অক্ষ বরাবর একক ভেক্টর (unit vectors)। এই বল তো পাথরটিকে ঠেলে বৃত্ত থেকে বার করে দেবে , পাথর তো ঘুরে B’র দিকে আসবে না। এর মানে ঘূর্ণায়মান পর্যবেক্ষক (Rotating observer) centrifugal force ছাড়াও আরোও pseudo force দেখবে। এই বল হতে হবে tangential direction-এ– নইলে পাথর B’র দিকে আসতে পারবে না। এই ক্ষেত্রে শুধু tangential নয় clockwise-ও হতে হবে। বলা বহুল্য বল’টি ω=0 হলে থাকতে পারে না। তাই নিশ্চই ω-এর সমানুপাতিক। আগের উদাহরণ থেকে দেখাই বেগ যখন শূন্য তখন এই বল’টিও শূন্য। ঘর্ষণের জন্য পাথর যখন স্থির ছিল তখন এই বল ছিল না। centrifugal force-এর জন্য radial velocity তৈরী হলে তবে এই tangential force-টি আসবে। ω (z-বরাবর)
এবং v vector-এর ওপর নির্ভরশীল এই বল-টাকে ভাঙা যেতে পারে m(v x ω) [তাহলে clockwise tangential component থাকবে এবং dimension মিলবে] কিন্তু coefficient-এ যে কোনো একটি সংখ্যা বসতে পারে। সত্যিকারের হিসেব ছাড়া এই বলটির ঠিক রূপ লেখা সম্ভব নয়। আমরা যে পথে এগিয়েছি সেটা কিছুটা intuitive । যাই হোক , এই রাস্তা ধরে এগোলে coefficient-টাও বেরিয়ে আসবে। ধরা যাক coefficient-টি α, তাই বলটাকে লেখা হল m α(v x ω)। এটায় পর্যবেক্ষক B কি দেখবে ? পর্যবেক্ষক B দেখবে পাথরটি তার দিকে এগিয়ে আসছে r ব্যাসার্ধের বৃত্তের পরিধি ধরে (along a circle of radius r)।
তাহলে পর্যবেক্ষক B বলবে পাথরের ত্বরণ ω2r কারণ পাথরের গতিবেগের মান v = ωr। সমস্ত গতি এখানে ঘুর্ণনবেগ ω-এর জন্য। এই ত্বরণ কেন্দ্রবিন্দুর দিকে। B এখন পর্যন্ত জানে পাথরের ওপর centrifugal force আছে mω2r বাইরের দিকে। নতুন যে force-টির কথা হচ্ছে সেটাকে হতে হবে তাহলে কেন্দ্রবিন্দুর দিকে — cross product rule-এর সাহায্যে সহজেই বোঝা যাচ্ছে v x ω কেন্দ্রের দিকে। তাহলে কেন্দ্রাভিমুখ বল (force towards the center) αm (v x ω) = αmω2r এবং অপকেন্দ্রিক বল (force away from the center) mω2r । নিউটনের দ্বিতীয় সূত্র হিসেবে B লিখবে αmω2r – mω2r = ভর x ত্বরণ = mω2r, অতএব আমরা পাচ্ছি , α= 2 ।
Rotating frame of reference-এ যে এই নতুন pseudo force-টা পাওয়া গেল, তার নাম কোরিওলিস বল (Coriolis force),
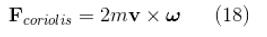
ঘুর্ণায়মান পর্যবেক্ষক ω constant (ধ্রুব) হলে এই দুটি pseudo force দেখে (centrifugal + coriolis)। যদি ω বদলায় তাহলে একটি তৃতীয় pseudo force তৈরী হয়। তাই আমাদের উদাহরণের পর্যবেক্ষক B Newton’s second law লিখবে (vector notations-এ) :
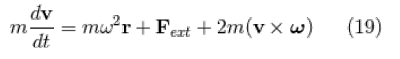
যদি দ্বিমাত্রিক গতি হয় তাহলে ,
এইবার আমরা এই force equation-টা ধরে নিয়ে পর্যবেক্ষক B’র জন্য সত্যি সত্যিই অঙ্ক কষে দেখাব যে পাথরের গতিপথ B’র চোখে একটি বৃত্তাকার পথ। Fext = 0 এই ক্ষেত্রে এবং component-এ ভেঙে নিয়ে লিখলে Eq (19) হবে,
এই দুটি coupled equation-এর সমাধানের জন্য ব্যবহার করা হয় (
) সহজেই দেখা যায় ,
Second order differential equations with constant coefficient-এর সমাধানের চেহারা হয় , তাই
লিখলে (যেখানে A ধ্রুবক),
Repeated roots হওয়ায় দুটি independent solutions হবে , এবং
। Cএবং D যদি Constants of integration হয় তাহলে,
এবং
এইবার C এবং D নির্ধারণ করতে হবে initial conditions-এর সাহায্যে । পর্যবেক্ষক B দেখবে যখন t = 0 , m-এর অবস্থান (0, r) -এ। তাই আর পাথরের গতিবেগ হিসেবে t = 0 সময়ে সে দেখবে
(নিজের গতিবেগের ঠিক উল্টোটা)। তাই
, Eq (23) থেকে t = 0 সময়ে পাই
এবং
– এর যে রূপ (expression) দেওয়া আছে Eq (23) এর নীচে, তার থেকে পাই
। অতএব এই প্রাথমিক শর্ত ব্যবহার করে ,
Real এবং imaginary parts আলাদা করলে,
সময়ে
এবং
, তাই B দেখবে পাথরটি এসে তার সঙ্গে ধাক্কা খেলো। Eq (25) B-এর চোখে পাথরটির গতি সম্পূর্ণ রূপে দিয়ে দিচ্ছে । একটু ভাবলেই বোঝা যাবে উত্তরটা সম্পূর্ণ সত্যি। এটাও এবার খুব সহজে বুঝে নিতে পারবে যে Eq (18)-এ 2 ছাড়া অন্য কোনো prefactor বেরোলে unphysical answers আসতো।
এতটা সময় কেন ঘূর্ণায়মান পর্যবেক্ষকের ওপর কাটালাম ? পৃথিবীর নিজের অক্ষের ঘূর্ণনের জন্য আমরা সবাই ঘূর্ণায়মান পর্যবেক্ষক! 24 ঘন্টায় radian ঘোরাটা খুবই অল্প ঘূর্ণন বেগ। কিন্তু যখন হাওয়ায় গতি এবং আবহাওয়ার পূর্বাভাস প্রয়োজন তখন এই Coriolis force কে বিশ্লেষণে অন্তর্ভুক্ত করতেই হবে ।
Non inertial frame-এর আরেকটি সহজ উদাহরণ constant gravitational field-এ পাওয়া যায়। পৃথিবীর উপরিতলের (surface)-এর কাছাকাছি থাকলে , পৃথিবীর gravitational field-টা একটা constant acceleration তৈরী করে যেটা আমরা “g” হিসেবে লিখি। যে কোনে বস্তু যার ভর “m”, সে পৃথিবীর কেন্দ্রবিন্দুর দিকে আকৃষ্ট হবেই একটি বল mg দিয়ে। পর্যবেক্ষক যেখানে দাঁড়িয়ে আছে সেখনে সে দেখবে প্রত্যেকটা বস্তুর ওপর বলটা উল্লম্বভাবে নিচের দিকে (vertically downwards)। এবার আমরা বলতেই পারি যদি gravitational mass এবং inertial mass সমান হয় তাহলে এমন একটি reference frame যদি নেওয়া যায় যেটি “g” acceleration নিয়ে নীচের নামছে, সেই frame-এ প্রত্যেকটি বস্তুর ওপর থাকবে pseudo force mg upwards এবং সম্পূর্ণ ভাবে cancel করে দেবে gravitational force mg downwards। এই reference frame-এ gravitational field-এর অস্তিত্ব আর বোঝা যাবে না।
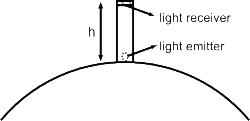
উপোরক্ত ছবির সাহায্যে একটি সিদ্ধান্তে আসা যায় যেটা পদার্থবিজ্ঞানের ইতিহাসে বেশ গুরুত্বপূর্ণ ছিল। ধরা যাক পৃথিবীতে কোথাও একটা “h” উচ্চতার tower রয়েছে (Fig 11)। Tower-এর তলা থেকে উপরের দিকে আলো ফেলা হচ্ছে। আলোর frequency (কম্পাঙ্ক) ν । Tower-এর মাথায় রয়েছে একটি receiver ।
প্রশ্ন : ঐ recevier কি আলোর frequency ν-ই দেখবে না অন্য কিছু ?
হিসেবের সুবিধার জন্য আলোর চরিত্রটা নেব কণাভিত্তিক। আলোর কণা হচ্ছে photon । কোনো উৎস থেকেν frequency-তে আলো বেরোনো মানে T= 1/ν সময় পরপর photon নির্গত হচ্ছে । যে কোনো frame-এ আলোর কণার গতি c= 3 x 108 m/sec ।
এবারে পরপর দুটি photon নির্গমণের ঘটনা বিশ্লষণ করা যাক এমন একটি reference frame থেকে যেটি কিনা g ত্বরণ নিয়ে নীচের দিকে পড়ছে। এই frame-এ কোনো gravity নেই । Fig (12)-এ ঘটনাবলীর ছবি দেওয়া হল।
‘g’ ত্বরণে নেমে যাওয়া পর্যবেক্ষক দেখবে:
1)Tower এর তলদেশের অবস্থান বদলাচ্ছে অনুসারে,
2) Tower এর ছাতের অবস্থান বদলাচ্ছে অনুসারে,
3) প্রথম photon বেরোলে z = 0 থেকে t = 0 সময়তে । ধ্রুবগতি c -তে চললে অতিক্রান্ত পথ হবে ,
4) সময় -তে দ্বিতীয় photon বেরোবে, সে চলবে
থেকে এবং ধ্রুব গতিবেগ c নিয়ে ,তার পথ হবে
5) প্রথম photon ছাতে পৌঁছাবে t1 সময়ে যখন
6) দ্বিতীয় photon ছাতে পৌঁছাবে t2 সময়ে যখন
যদি g=0 হয় (no acceleration , hence no gravity) তাহলে Eqs (26)এবং (27) থেকে আমরা পাবো , receiving frequency = emitting frequency.
যদি g ≠0 হয় তাহলে (27) থেকে (26) বিয়োগ করলে
Eq (26)এবং (27) যোগ করলে
যেহেতু এবং
(
= আলোর তরঙ্গ দৈর্ঘ্য )
Eq (29) থেকে আমরা পাই এবং Eq (28) হয়ে দাঁড়ায়
অথবা,
যে আলো পৌঁছেছে Tower-র ওপর তার frequency
.
অতএব gravitational field-এ আলোর তরঙ্গ দৈর্ঘ্য বদলে যায় – আইনস্টাইনের সাধারণ আপেক্ষিক তত্ত্বের তিনটি বড় predictions-এর একটি। 1959 সালে একটি বিখ্যাত experiment-এ Harvard University তে Pound এবং Rebka 22.5m উঁচু একটা tower ব্যবহার করে এই ক্ষুদ্রানুক্ষুদ্র effect ( !!) laboratory-তে demonstrate করেন। এটা সহজেই অনুমান করতে পারবে কি ধরণের ভয়ানক চিন্তাশক্তি ও সৃজনশক্তির সাহায্যে এত ছোট একটি effect ধরা গিয়েছিল !
(সমাপ্ত)
কভারের ছবি: জয়ন্ত মন্ডল। ফোর্স ডায়াগ্রাম: শুভায়ু আলি