[ আগে যা হয়েছে: প্রথম পর্বে আমরা শুরু করেছিলাম জ্যামিতিতে আদৌ কিছু দেওয়া আছে কিনা এই প্রশ্ন দিয়ে, দেখেছিলাম যে ইউক্লিডীয় জ্যামিতির স্বতঃসিদ্ধগুলো আসলে সেই দেওয়া থাকা জিনিসগুলো। কিন্তু কি বলছে সেগুলো? প্রথম পর্বে শুধুই প্রথম স্বতঃসিদ্ধ কি বলছে দেখেছিলাম। দ্বিতীয় পর্বে দেখেছি জ্যামিতির বীজগাণিতিকরণ হয়ে কিভাবে কার্তেসীয় স্থানাঙ্ক জ্যামিতি এল, আর এই স্থানাঙ্ক জ্যামিতির হাত ধরে আমরা দেখলাম যে দ্বিতীয়, তৃতীয় আর চতুর্থ স্বতঃসিদ্ধ কি বলছে। ইউক্লিডীয় দূরত্ব অপেক্ষক আর ইউক্লিডীয় ইনার প্রোডাক্ট কেও চিনলাম সেই পর্বেই। তৃতীয় পর্বে সমস্তটা জুড়েই আমরা মাথা ঘামিয়েছি পঞ্চম স্বতঃসিদ্ধ নিয়ে। দেখলাম পঞ্চম স্বতঃসিদ্ধ কি বলছে আর দেখেছি সেই স্বতঃসিদ্ধ কে পালটে নিলেও আমরা জ্যামিতি পাই, শুধু সেই জ্যামিতি আর ইউক্লিডীয় জ্যামিতি নয়, অনিউক্লিডীয় জ্যামিতি। এই পর্বে আমরা অনিউক্লিডীয় জ্যামিতির অদ্ভুত অথচ মজার জগতটাকে চিনব। ]
( তৃতীয় অংশের পর )
অনিউক্লিডীয় জ্যামিতি – গোলকের উপরে কীভাবে সরলরেখা আঁকব?
অনিউক্লিডীয় জ্যামিতিগুলো আসলে কি বলছে এইটা বুঝতে আমরা প্রথমে শুরু করব আপাতভাবে একদম অন্য কিছু প্রশ্ন থেকে। আমরা প্রথমে দেখব যে গোলকের উপরিতলে আমরা যদি জ্যামিতি করতে চাই, কেমন দেখতে হবে সেই জ্যামিতি? আমাদের কিন্তু মাথায় রাখতে হবে যে জ্যামিতিটা গোলকের উপরিতলেই হওয়া চাই । কোন কিছু, যেমন ধরা যাক কোন রেখা যদি ওই তলটা ছেড়ে বেরিয়ে যায় বা গোলকটা ফুঁড়ে চলে যায় তাহলে সেইটা এই জ্যামিতির অংশ নয় আর।
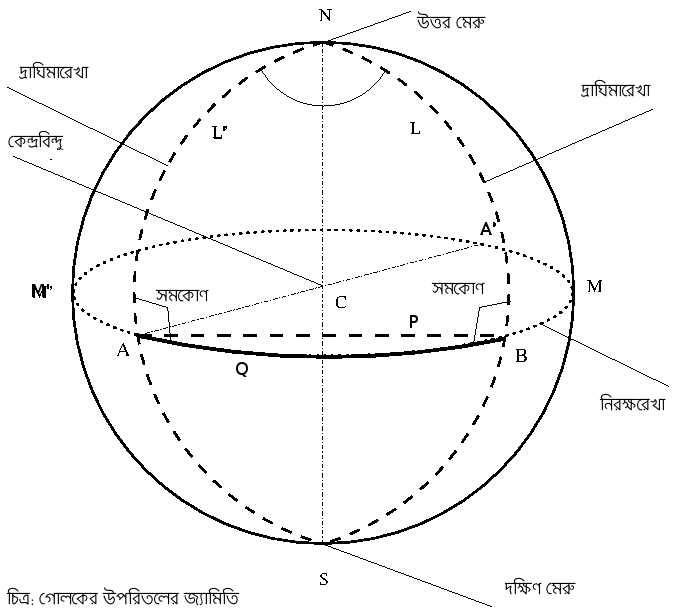
ধরা যাক, একটা গোলকের উপরে একটা ‘সরলরেখা’ আঁকব আমরা, শুরু করব সরলরেখাংশ দিয়ে। পৃথিবীর অক্ষাংশ-দ্রাঘিমাংশের মতই গোলকটার সবচেয়ে উপরের বিন্দুটাকে (উপরের ছবিতে N বিন্দু) আমরা গোলকটার উত্তর মেরু, সবচেয়ে নিচের বিন্দুকে দক্ষিণ মেরু (উপরের ছবিতে S বিন্দু), ঠিক পেট বরাবর আড়াআড়ি যাওয়া বৃত্তকে নিরক্ষরেখা ( উপরের ছবিতে ABMA’M’A বৃত্ত ) আর উত্তর মেরু ও দক্ষিণ মেরুকে লম্বালম্বি জুড়ছে যে অর্ধবৃত্তগুলো তাদেরকে দ্রাঘিমারেখা (উপরের ছবিতে NL’AS আর NLBS দুটো দ্রাঘিমারেখা) বলব।
এইবার ধরা যাক নিরক্ষরেখার উপরে আমরা দুটো আলাদা বিন্দু নিয়েছি আর তাদের মধ্যে দিয়ে যাওয়া ‘সরলরেখা’ টা আঁকতে চাইছি। ধরা যাক A আর Bবিন্দু দুটোর কথা। ওই বিন্দুদুটোর মধ্যে হ্রস্বতম দূরত্বের পথ কোনটা?
মহাবৃত্তরাই গোলকের উপরিতলের জ্যামিতিতে ‘সরলরেখা’!
একটু ভাবলে সহজেই বোঝা যাবে যে নিরক্ষরেখা বরাবর যে দুটো বৃত্তাংশ ওই বিন্দু দুটোর মধ্যে দিয়ে গেছে, অর্থাৎ একটা পথ যেটা A বিন্দু থেকে শুরু হয়ে অন্যটায় (B বিন্দুতে) পৌঁছেছে (AQB বৃত্তাংশটা), আর একটা পথ ঘুরিয়ে নাক দেখানোর মত করে প্রায় গোটা গোলকটা ঘুরে এসে অন্য বিন্দুটায় পৌঁছেছে (AM’A’MB বৃত্তাংশটা), এই দুটো পথের যেটার দৈর্ঘ্য কম সেইটা, অর্থাৎ AQB বৃত্তাংশটা। গোলমেলে লাগছে? ওই দুটো বিন্দুকে যোগ করা সরলরেখার (সাধারণ অর্থে, মানে APB সরলরেখাংশটা) অংশটার দৈর্ঘ্য তো অবশ্যই আরও কম। ঠিকই, কিন্তু মুশকিল হল ওই সরলরেখাটা গেছে গোলকটাকে ফুঁড়ে, ফলত গোলকের উপরিতল ছেড়ে বেরিয়ে গেছে সেটা, তাই ওটা গোলকের উপরিতলটার উপর ‘সরলরেখাংশ’ তো দূর, কোনরকম ‘রেখা’ ই নয়। একবার এই ধাঁধাঁটা কেটে গেলেই উপরিতলের পথগুলোর মধ্যে কেন এই পথটাই হ্রস্বতম বোঝা কঠিন নয়, উৎসাহীরা এমনকি একটা বল আর সুতো নিয়ে হাতেকলমে মিলিয়েও নিতে পারেন। অবশ্যই গাণিতিকভাবেও প্রমাণ করা সম্ভব এটা, কিন্তু আমরা সেই অঙ্কের কচকচিতে ঢুকব না১।
এইবারে আমরা দেখব Aআর B দিয়ে যাওয়া ‘সরলরেখা’ টা কোনটা? AQB বৃত্তাংশটাকে দুদিকে অসীম বর্ধিত করলে সরলরেখাটা পাব, তাই নিরক্ষীয় বৃত্তটাই এই সরলরেখা। বস্তুত ঠিক একই ভাবে গোলকের উপরিতলে যেকোন দুটো বিন্দু দিয়ে যাওয়া ‘সরলরেখা’ টা হবে গোলকের কেন্দ্রবিন্দুকে কেন্দ্র করে ওই বিন্দু দুটো দিয়ে যাওয়া বৃত্তটা … এইরকম বৃত্তগুলোকে বলা হয় মহাবৃত্ত (great circle)।
অর্থাৎ, মহাবৃত্তরাই গোলকের উপরিতলের জ্যামিতিতে ‘সরলরেখা’!
কিন্তু, এই ‘সরলরেখা’ কি আমাদের পরিচিত সরলরেখা?
অর্থাৎ এরই মধ্যে আমরা এমন কিছু ‘সরলরেখা’ পেয়েছি যাদের সাথে সরলরেখা বলতে যা বুঝি তার বিস্তর ফারাক… প্রথমত, এরা আদৌ ‘সোজা’ নয়, দিব্যি বাঁকা; দ্বিতীয়ত, ‘ অসীম বর্ধিত’ করা সত্ত্বেও এরা আদৌ অসীম পর্যন্ত বিস্তৃত নয়, বদ্ধ ( bounded)২। এই দ্বিতীয়টায় অবশ্য অবাক হওয়ার সত্যিই কিছু নেই, কারণ আমাদের জ্যামিতিক স্থানই ( গোলকের উপরিতল) এক্ষেত্রে বদ্ধ।
আপনাদের মনে থাকতে পারে যে প্রথম পর্বে ( এখানে দেখুন ) বলেছিলাম যে, যার ওপরে আমরা জ্যামিতি কষব সেই জিনিসটা অসীম, কিন্তু এখানে দেখছি যে বদ্ধ (অর্থাৎ সসীম) জিনিসের উপরেও আমরা জ্যামিতি কষতে পারি। সেটা কিভাবে সম্ভব? আমরা প্রথম পর্বে বলেছিলাম ইউক্লিডীয় জ্যামিতির কথা। ইউক্লিডীয় স্থান খাতার পাতার মত সামতলিক (flat), আর তাতে আঁকা-বাঁকা, উঁচু-নীচু, ঢেউ খেলানো কিচ্ছু নেই। ইউক্লিডীয় স্থান সামতলিক বলেই তার উপরের সরলরেখা অসীম পর্যন্ত বিস্তৃত। কিন্তু অনিউক্লিডীয় স্থানে, যেমন ধরা যাক গোলকের উপরিতলে, সেরকম যে হতেই হবে তার কোন মানে নেই। অনিউক্লিডীয় জ্যামিতির আবিষ্কারই স্থানের ‘বক্রতা’ (curvature)-র প্রশ্নটাকে সামনের সারিতে নিয়ে এল।
প্রসঙ্গত, বিভিন্ন ধরণের জ্যামিতিতে ‘সরলরেখা’ রা, সাধারণ অর্থে সরলরেখা বলতে যা বুঝি তার থেকে বেশ আলাদা হতে পারে এইটা বোঝা যাওয়ার পর এদের একটা নাম দেওয়া হল, সাধারণ সরলরেখার থেকে আলাদা করে বোঝার জন্য। এদেরকে বলে জিওডেসিক (geodesic)। সাধারণ অর্থে সরলরেখারাও কিন্তু জিওডেসিক, তারা ইউক্লিডীয় স্থানের জিওডেসিক।
গোলকের উপরে ত্রিভুজের তিনকোণের সমষ্টি কি ১৮০ ডিগ্রী?
কিন্তু এই যে গোলকের উপরিতল কে অনিউক্লিডীয় স্থান বললাম, দেখেই নেওয়া যাক এর উপরের জ্যামিতি সত্যিই অনিউক্লিডীয় কিনা। কিভাবে দেখব? ইউক্লিডীয় জ্যামিতিতে ত্রিভুজের তিনটে কোণের যোগফল দুই সমকোণ, তাই প্রথমে আমরা দেখব এই জ্যামিতিতে ‘ত্রিভুজ’-এর তিনটে কোণের যোগফল কত। কোণ মাপব কি করে? দুটো বক্ররেখা যেখানে ছেদ করেছে, সেই বিন্দুতে বক্ররেখা দুটোর স্পর্শক (tangent) টানব, স্পর্শকদুটোর মধ্যে উৎপন্ন কোণই বক্ররেখাদুটোর মধ্যের কোণ। প্রসঙ্গত বলে রাখি যে অনিউক্লিডীয় জ্যামিতি আবিষ্কারের বহু আগে থেকেই এই পদ্ধতিটা জানা। ইউক্লিডীয় জ্যামিতিতে দুটো বক্ররেখার মধ্যেকার কোণ এভাবেই মাপা হয়।
এরপর আর বুঝতে একটুও অসুবিধে হওয়ার কথা নয় যে গোলকের উপরিতলে প্রতিটা দ্রাঘিমারেখা নিরক্ষরেখাকে লম্বভাবে ছেদ করেছে ( উপরের ছবিতে NL’AS আর NLBS দ্রাঘিমারেখাদুটো যথাক্রমে A আর B বিন্দুতে নিরক্ষরেখার ওপর লম্ব )। এখন নিরক্ষরেখার ওপরে যেকোন দুটো আলাদা বিন্দুকে আর উত্তরমেরুকে তৃতীয় শীর্ষবিন্দু ধরে আঁকা ‘ত্রিভুজ’ টার কথা ভাবি ( উপরের ছবিতে NL’AQBLN‘ ত্রিভুজ’টা, যার শীর্ষবিন্দু তিনটে হল N,A,B বিন্দুগুলো )। খেয়াল রাখতে হবে এইরকম ‘ত্রিভুজ’-এর বাহুরা কিন্তু ‘সরলরেখা’ হতে হবে, অর্থাৎ জিওডেসিক হতে হবে… আর সেইজন্যে, সাধারণ অর্থে ত্রিভুজ বলতেই আমরা যা ভাবি তার থেকে আলাদা করার জন্য এইরকম ত্রিভুজকে ‘জিওডেসীয় ত্রিভুজ’ (geodesic triangle) বলা হয়। তা সে যাই হোক, মোদ্দা বিষয়টা হল উত্তরমেরু আর নিরক্ষরেখার ওপরে যেকোন দুটো আলাদা বিন্দু দিয়ে আঁকা ত্রিভুজটার ভূমি নিরক্ষরেখার অংশ, আর অন্য দুটো বাহু দুটো দ্রাঘিমারেখার অংশ, এবার যেহেতু দুটো দ্রাঘিমারেখাই নিরক্ষরেখাকে লম্বভাবে ছেদ করেছে, ভূমির উপরে তৈরি হওয়া কোণদুটোর যোগফলই দুই সমকোণ অর্থাৎ একশ আশি ডিগ্রী । তাই উত্তরমেরুর শীর্ষকোণটার মান যাই হোক না কেন, এই ত্রিভুজটার তিনটে কোণের যোগফল দুই সমকোণের চেয়ে বেশী হতে বাধ্য। আমরা এই বিশেষ ত্রিভুজটা নিয়েছিলাম অবশ্যই নেহাত বোঝার সুবিধের জন্য, এই জ্যামিতিতে যেকোন ত্রিভুজের জন্যই এটা সত্যি। আরও একটা জিনিস খেয়াল করার, যে এই জ্যামিতিতে যেহেতু ত্রিভুজের তিনটে কোণের যোগফল সবসময় দুই সমকোণের বেশী তাই এই জ্যামিতি অধিবৃত্তীয় নয়, উপবৃত্তীয় ।
গোলকের উপরের জ্যামিতি উপবৃত্তীয় জ্যামিতির উদাহরণ – এখানে ত্রিভুজের তিনটি কোণের সমষ্টি দুই সমকোণের বেশী!
উপবৃত্তীয় ও অধিবৃত্তীয় জ্যামিতি
গোলকের উপরের জ্যামিতি যে উপবৃত্তীয় সেটা আমরা আরও একভাবে দেখতে পারি। সমান্তরাল সরলরেখায় ফিরে এসে। ধরা যাক, আমাদের একটা সরলরেখা হল নিরক্ষরেখা। নিরক্ষরেখার ওপরে নয় এরকম আর একটা বিন্দু নিলাম। এই বিন্দু দিয়ে নিরক্ষরেখার সমান্তরাল করে কটা সরলরেখা আঁকা যাবে? একটাও না। কারণ অন্য বিন্দুটি দিয়ে যাওয়া যেকোনো সরলরেখাই যেহেতু আর একটা মহাবৃত্ত, সেটা নিরক্ষরেখাটাকে দুটো বিন্দুতে ছেদ করবেই, তাই অন্য কোন সরলরেখাই নিরক্ষরেখার সমান্তরাল হবে না।
এই জ্যামিতিটা থেকেও উপবৃত্তীয় জ্যামিতি নামটারও কারণ বোঝা যাবে, কারণ বৃত্ত যেমন একটা বিশেষ ধরণের উপবৃত্ত (ellipse) , তেমনি গোলকও একটা বিশেষ ধরণের উপবৃত্তক ( ellipsoid, একটা উপবৃত্তাকার পাতকে তার কোন একটা অক্ষ বরাবর ঘুরপাক খাওয়ালে যে ঘনবস্তুটা পাব সেইটা।
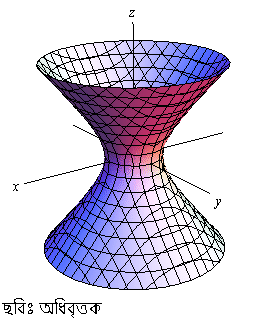
এইভাবে পাতের মত জিনিসকে ঘুরপাক খাইয়ে তৈরি করা যায় এরকম জিনিসগুলোকে volume of revolution বলে, তাই উপবৃত্তক উপবৃত্ত থেকে যে volume of revolution টা পাওয়া যায় সেইটা )। ঠিক তেমনি একটা অধিবৃত্তকের ( hyperboloid, একটা অধিবৃত্তাকার পাতকে তার অক্ষ বরাবর ঘোরালে যে ঘনবস্তুটা পাব। অধিবৃত্তকের উপরিতলটা অনেকটা বেতের মোড়ার গা টার মত দেখতে ) উপরিতলের জ্যামিতিটা অধিবৃত্তীয় জ্যামিতি।
ওইরকম জ্যামিতিতে আবার স্থান মোটেই বদ্ধ নয়, কারণ অধিবৃত্ত অসীম পর্যন্ত বিস্তৃত। তাই এরকম তলের উপরের জিওডেসিকরাও অসীম পর্যন্ত বিস্তৃত অধিবৃত্ত। জিওডেসিক ত্রিভুজের তিনটে কোণের যোগফলও সর্বদা দুই সমকোণের কম।
তাহলে এ পর্যন্ত আমরা দেখলাম যে ইউক্লিডের পঞ্চম স্বতঃসিদ্ধ ( এখানে দেখুন ) আসলে বাস্তবিকই একটা স্বতঃসিদ্ধ আর সেটা কি বলে সেটাও খানিকটা ধারণা পেলাম। কিন্তু তার সাথে সাথেই উঠে এল নতুন প্রশ্নও। পর্ব দুই এ আমরা দেখেছিলাম যে ইউক্লিডীয় জ্যামিতির বীজগাণিতিকরণ, দেখেছিলাম ইউক্লিডীয় স্থান আর ইউক্লিডীয় ইনার প্রোডাক্টটা দেওয়া থাকলেই ইউক্লিডীয় জ্যামিতি নেহাতই বীজগণিতের হিসেব কষা মাত্র। এই বাঁকা স্থানেও কি সেরকম কিছু করা সম্ভব?
এই প্রশ্নটারই উত্তর দিয়েছিলেন রীমান, দেখিয়েছিলেন সম্ভব। তার এই বৈপ্লবিক কাজের সম্মানে আজকের জ্যামিতি সবচেয়ে গুরুত্বপূর্ণ বিভাগকে আমরা বলি রীমানীয় জ্যামিতি ( Riemannian geometry ) আর তার পরের সবচেয়ে গুরুত্বপুর্ণ বিভাগটার নাম আধা-রীমানীয় জ্যামিতি ( semi-Riemannian বা pseudo-Riemannian geometry )।
রীমানের উত্তরটা বুঝতে আমাদের একটু সময় লাগবে, তাই আমরা আসতে আসতে এগোব।
ইউক্লিডীয় দূরত্ব-অপেক্ষক
প্রথমে আমরা ফেরত যাব ইউক্লিডীয় স্থানাঙ্ক জ্যামিতিতেই। পর্ব দুইতে ( এখানে দেখুন ) ইউক্লিডীয় দূরত্ব-অপেক্ষকের তিনটে ধর্ম বলেছিলাম। ধর্ম তিনটে হল:
(1) d(a,b)≥0, একমাত্র যদি a=b হয়, তাহলেই d(a,b)=0
(2) d(a,b)=d(b,a)
(3) d(a,c)≤d(a,b)+d(b,c)
বস্তুত রীমান যতদিনে জ্যামিতির কাজ করছেন, ততদিনে অঙ্কের অন্যান্য বিভাগেও আমাদের জানা-বোঝা খানিক এগিয়েছিল। তাই থেকে ততদিনে এইটা বোঝা গিয়েছিল যে এই ধর্ম তিনটে থাকলে যেকোন এরকম অপেক্ষকই দূরত্ব-অপেক্ষকের কাজ করতে পারে।
আরও একটা জিনিস খেয়াল করার যে ইউক্লিডীয় দূরত্ব-অপেক্ষকের সূত্রটি হল:
(d(a,b))2=(a1-b1)2+(a2-b2)2+…+(an-bn)2
এখানে a1,a2,…,an এইগুলো হল a বিন্দুটার স্থানাঙ্ক আর b1,b2,…,bn হল b বিন্দুটার স্থানাঙ্ক। বলে রাখা ভালো, দূরত্ব-অপেক্ষকের এই সূত্রটি হল homogeneous quadratic polynomial বা সমসত্ত্ব দ্বিঘাত পলিনমিয়ালের একটি উদাহরণ। এইধরনের homogeneous কোয়াড্রাটিক পলিনমিয়াল অবশ্য আরো অনেকরকমের হতে পারে। তাই গণিতজ্ঞরা এই ধরনের পলিনমিয়ালকে সাধারণত নীচের সাধারণ আকারে লিখে থাকেন।
f(x) =f( x1,…,xn) = ∑n(i,j=1) gij xi xj,
যেখানে এই gij গুলো যেকোন বাস্তব সংখ্যা হতে পারে, আর x1, x2,…,xn হল x বিন্দুর স্থানাঙ্ক। এইবারে দূরত্ব-অপেক্ষকের সাধারণ ফর্মুলা a-bভেক্টরের সমসত্ত্ব দ্বিঘাত পলিনমিয়াল, তাই সেটার সাধারণ চেহারা হবে,
(d(a,b))2= ∑n(i,j=1) gij (ai-bi)(aj-bj)
যেমন, ইউক্লিডীয় দূরত্ব-অপেক্ষকের ফর্মুলাতে, যদি i আর j আলাদা হয়, মানে ধরুন যদি i = ১ আর j = ২ হয়, তাহলে আর যদি i আর j সমান হয়, মানে ধরুন যদি i = ১ আর j = ১ হয়, তাহলে gii=১।
এই ফর্মুলাটাকেই ম্যাট্রিক্স বা সারণী ব্যবহার করে আরও একভাবে লেখা যায়:
(d(a,b))2 =xTG x। এখানে G হল gij দিয়ে গড়া একটা n x n ম্যাট্রিক্স, মানে এই ম্যাট্রিক্সটার i-তম row আর j-তম column এ রয়েছে gij। আর x হল (ai – bi ) দিয়ে গড়া একটা column বা স্তম্ভ ম্যাট্রিক্স, অর্থাৎ x এর i-তম row তে আছে xi= ai–bi । এখানে মানে এর ট্রান্সপোজ, অর্থাৎ কে স্তম্ভের আকারে না লিখে সারির আকারে লিখলে যা হবে, মানে row matrix আকারে লিখলে, আর পাশাপাশি চিহ্নগুলো লেখার মানে ম্যাট্রিক্সগুলোকে গুণ করা হয়েছে, ম্যাট্রিক্সের গুণ। গুণটা করে ফেলে ফর্মুলায় লিখলে দাঁড়াবে,
xTG x= ∑n(i,j=1) gij xi xj
ট্রান্সপোজ যে অবশ্য শুধু সারি ভেক্টর বা স্তম্ভ ভেক্টরেরই করা যায় এমন নয়, যেকোন ম্যাট্রিক্সেরই করা যায়, সারিগুলোকে স্তম্ভ করে দিলেই ( আর তার মানেই স্তম্ভগুলো সারি হয়ে যাবে ) যে নতুন সারণীটা পাব সেটাই আগের ম্যাট্রিক্সটার ট্রান্সপোজ ম্যাট্রিক্স।
যেহেতু দূরত্ব-অপেক্ষককে উপরের তিনটে ধর্ম মেনে চলতে হয়, তাই gij গুলো যা ইচ্ছে তাই হতে পারে না। আর সেই জন্য G ম্যাট্রিক্সটাকেও বেশ কয়েকটা ধর্ম মেনে চলতে হয়।
প্রথম ধর্মটার জন্য G ম্যাট্রিক্সটাকে পজিটিভ-ডেফিনিট হতে হবে, অর্থাৎ xTG x≥0 হতে হবে, আর একমাত্র তখনই হবে যখন , অর্থাৎ ai = bi হবে।
দ্বিতীয় ধর্মটার জন্য সবসময় gij=gji হতে হবে। তাই G এর i-তম row আর j-তম column এ যে সংখ্যা আছে তার মান আর j-তম row আর i-তম column এ যে সংখ্যা আছে তার মান একই হতে হবে। এই ধরনের ম্যাট্রিক্সটাকে সিমেট্রিক( symmetric ) ম্যাট্রিক্স বলে। শর্তটা থেকেই এমন নামেরও কারণ বোঝা যাচ্ছে। এরকম ম্যাট্রিক্সের বাঁদিকের উপর থেকে ডানদিকের নিচের কোণা অবধি কর্ণটাকে একটা আয়নার মত ভাবলে কর্ণের টার্মগুলো বাদে অন্য টার্মগুলো প্রত্যেকটা তার দর্পণ-প্রতিবিম্বটার সাথে সমান। যেমন ইউক্লিডীয় দূরত্ব-অপেক্ষকের ক্ষেত্রে এই G ম্যাট্রিক্সটা দেখতে হবে এইরকম –
মানে শুধু কর্ণটায় ১ আছে, বাকি সব জায়গায় ০।
এইটা সিমেট্রিক। আবার ২x২ সিমেট্রিক ম্যাট্রিক্স এর উদাহরণ হিসেবে ভাবা যেতে পারে
ম্যাট্রিক্সটার কথা ।
তৃতীয় ধর্মটার জন্য অবশ্য কিছুই চাই না, কারণ আমরা এখনো অবধি যা যা ধরে নিয়েছি তার থেকেই ওই ধর্মটা ফাউ হিসেবে পাওনা।
একটু খেয়াল করলেই বোঝা যাবে যে পর্ব দুই এর ইউক্লিডীয় দূরত্ব-অপেক্ষকের উদাহরণটার মতই এক্ষেত্রেও এই দূরত্ব-অপেক্ষকটা আসছে একটা ইনার প্রোডাক্ট থেকেই। ইনার প্রোডাক্টটা কেমন দেখতে? বস্তুত এক্ষেত্রে x ও y, দুটো ভেক্টরের ইনার প্রোডাক্ট আসলে Gx ও y এর ইউক্লিডীয় ইনার প্রোডাক্ট। যেহেতু G সিমেট্রিক, তাই x ও Gy এর ইউক্লিডীয় ইনার প্রোডাক্ট ও তাইই। ফর্মুলায় লিখলে দাঁড়াবে,
<x,y>=∑n(i,j=1) gij xi yj
আচ্ছা, এইবারে যদি আমরা প্রশ্নও করি যে যদি আমরা ইউক্লিডীয় স্থানের ওপরে এইরকম কোন একটা ইনার প্রোডাক্ট ব্যবহার করে ( ইউক্লিডীয় ইনার প্রোডাক্ট টা নয় ) পর্ব দুই এর মত বীজগাণিতিক হিসেবগুলো করতাম তাহলে যে জ্যামিতি পেতাম সেটা কিরকম জ্যামিতি? সেটা কি আমাদের কোন একটা অনিউক্লিডীয় জ্যামিতি দিত? উত্তরটা হল, দিত না আসলে । কেন দিত না সেটা পুরোপুরি বুঝতে হলে অনেক অঙ্কের কচকচিতে ঢুকতে হবে। সেদিকে আমরা যাব না, কিন্তু ধারণাগত জায়গা থেকে বোঝা যাবে খানিকটা। ওইরকম হিসেব নিকেশ করলে আমরা যা পেতাম সেটা আসলে ইউক্লিডীয় জ্যামিতিই, আর হিসেব নিকেশগুলো ও খুব অপরিচিত কিছু নয়। বস্তুত ওই হিসেবগুলো আসলে হেলানো অক্ষের কার্তেসীয় স্থানাঙ্ক জ্যামিতি ( oblique axes Cartesian co-ordinate geometry ) মাত্র। মানে সাধারণ কার্তেসীয় স্থানাঙ্ক জ্যামিতিই, শুধু অক্ষগুলো পরস্পরের ওপর লম্ব, এইটা ধরা হয়নি।
তাহলে অনিউক্লিডীয় জ্যামিতি কিভাবে পাব?
অনিউক্লিডীয় জ্যামিতি কিভাবে পাব? – সেইটার উত্তর বুঝতে প্রথমে আমাদের আগে ভাবতে হবে যে বাঁকা জিনিসের ওপরে জ্যামিতিটা করব কিভাবে? আমরা আগেই দেখলাম যে অনিউক্লিডীয় জ্যামিতিগুলো আসলে বাঁকা স্থানের জ্যামিতি, যেমন গোলকের উপরিতলটা বাঁকা, অথচ আমরা যা হিসেবনিকেশ করতে শিখেছি, এই ইনার প্রোডাক্ট আর দুরত্ব-অপেক্ষক দিয়ে, সেগুলো ইউক্লিডীয় স্থানেই কাজ করে। আসলে কেন ইউক্লিডীয় স্থানেই কাজ করে শুধু সেগুলো? সেটা খুব যে জরুরী আমরা যেটা বুঝতে চাইছি তার জন্য তা অবশ্য নয়, কিন্তু জিনিসটা মজার, তাই সেটাও আমরা একটুখানি দেখে নেব। আসলে ইনার প্রোডাক্ট নেওয়া যায় দুটো ভেক্টরের। ভেক্টর কাকে বলে? পদার্থবিদ্যায় ভেক্টর কাকে বলে আমরা জানি, কিন্তু অঙ্কে? অঙ্কে আসলে ভেক্টর বলতে শুধুই পদার্থবিদ্যার ভেক্টর বোঝায় এমন নয়। অঙ্কে ভেক্টর বলতে বোঝায় এরকম যেকোনো কিছুকেই, যার পদার্থবিদ্যার ভেক্টরের মত কিছু ধর্ম আছে। কোনগুলো?
আমরা পদার্থবিদ্যায় পড়েছি দুটো ভেক্টরকে যোগ করা যায়, করে যোগফল হয় তৃতীয় আর একটা ভেক্টর। সেখানে আমরা এটা করি সামান্তরিক সূত্র দিয়ে। আবার একটা ভেক্টরের সাথে একটা স্কেলার, মানে এক্ষেত্রে বাস্তব সংখ্যা দিয়ে গুণও করা যায়। অঙ্কে তাই যেকোনো সেট, যার যেকোনো দুই সদস্যকে ‘যোগ’ করে তৃতীয় একটা সদস্য কে পাওয়া যায় আর যাদের যেকোনো সদস্যকে একটা বাস্তব সংখ্যা দিয়ে গুণ করে দ্বিতীয় আর এক সদস্যকে পাওয়া যায়, সেরকম সেটগুলোকে বাস্তব ভেক্টর স্থান বা বাস্তব লিনিয়ার স্থান ( real vector space or real linear space) বলে। বস্তুত, ইউক্লিডীয় স্থানের প্রতিটি বিন্দুর অবস্থান সদিশ অর্থাৎ পজিশন ভেক্টর ( position vector) গুলোর সেট তা একটা বাস্তব লিনিয়ার স্থান। একটা ইনার প্রোডাক্ট আসলে একটা বাস্তব লিনিয়ার স্থানের ওপর একটা অপেক্ষক, যার মান একটা বাস্তব সংখ্যা, আর সেই মান দুটো ভেক্টরের উপর এমনভাবে নির্ভর করে যাতে যেকোনো একটা ভেক্টরকে একটা বাস্তব সংখ্যা দিয়ে গুণ করলে ইনার প্রোডাক্টের মানটাও সেই সংখ্যা দিয়ে গুণ হয়। ইনার প্রোডাক্ট সমেত একটা বাস্তব লিনিয়ার স্থান কে অঙ্কে বাস্তব ইনার প্রোডাক্ট স্থান (real inner product space ) বলে।
তাহলে এখন প্রশ্ন বাঁকা জিনিসের ওপর জ্যামিতি করতে আমরা লিনিয়ার স্পেস কোথায় পাব? উত্তরটা খুব সহজ আসলে, আর সেইজন্যেই বহুদিন লেগেছে এটা বুঝতে। কথাটা ভারী গোলমেলে শোনালেও অঙ্কে সুদূরপ্রসারী ভাবনাগুলো আসলে সবসময়েই ভীষণ সহজ। কঠিন, ধাঁধালো জিনিসের মধ্যে আরো বিদঘুটে কিছু নাম, খটমট কিছু সংজ্ঞা এইসব দিয়ে আসলে তাদের মধ্যেকার ভীষণ সহজ সরল সম্পর্কগুলোকে সামনে আনাই অঙ্কের কাজ, সেইটাই অঙ্কের মজা, তার সৌন্দর্য।
(পরের পর্বে সমাপ্য)
[১] আর একটা বিষয় — সাধারণভাবে সবসময়েই সরাসরি যাওয়া পথটাই ছোট হবে, ঘুরে আসা পথটার থেকে, কিন্তু এর একটা ব্যতিক্রম আছে, বিন্দু দুটো পরস্পর বিপ্রতীপ ( antipodal ) হলে , মানে একটা বিন্দু থেকে শুরু করে গোলকটা ভেদ করে গোলকের কেন্দ্র দিয়ে যাওয়া সরলরেখাটা ( সাধারণ অর্থে সরলরেখা ) গোলকের উপরিতলকে উলটোদিকে যে বিন্দুতে ছেদ করে সেইটাই যদি দ্বিতীয় বিন্দুটা হয়, যেমন Aআর A’ এর ক্ষেত্রে, তখন আর একমাত্র তখনই দুটো পথের দৈর্ঘ্য সমান, দুটো বিন্দু তখন নিরক্ষীয় বৃত্তকে সমান দুভাগে ভাগ করেছে, পথদুটো সেই অর্ধবৃত্ত দুটো (ছবিতে AM’A’ আর AQBMA’)। এতে সমস্যা কিছু নেই, কারণ আমরা এখুনি দেখব যে ‘সরলরেখা’টা একটাই, যে পথটাকেই সরলরেখাংশ ধরা হোক না কেন।
[২] প্রসঙ্গত, কিছু জায়গায় ‘সরলরেখা’ র ‘সংজ্ঞা’য় ‘অসীম পর্যন্ত বর্ধিত’ ই লেখা হয়, সেটা নিছক ভুল। infinitely extended আর extended upto infinity দুটোর অর্থে যে পার্থক্য হতে পারে এখানের আলোচনা তার একটা ভাল উদাহরণ। বস্তুত ‘অনির্দিষ্টভাবে বর্ধিত করলে’ ( extended indefinitely ) লেখাটাই সবচেয়ে নিরাপদ, কিন্তু দুর্ভাগ্যক্রমে ইউক্লিড এ অসীম শব্দটি রয়েছে।




[…] https://betapxs.wpengine.com/2015/07/05/elements-of-geometry-part-3/ https://betapxs.wpengine.com/2016/04/04/elements-of-geometry-part-4/ https://betapxs.wpengine.com/2017/06/03/elements-of-geometry-part-5/ […]