সমস্ত গতিবিদ্যার (Dynamics) শুরু নিউটনের তিনটি সূত্র (laws of motion) দিয়ে। তিনটি সূত্র এইরূপ:
1) কোনো বস্তুর ওপর বাইরে থেকে প্রযুক্ত বল (externally applied force) না থাকলে সেই বস্তুটি হয় স্থির থাকবে, নইলে সে যে গতিতে যেদিকে চলছিল, ঠিক সেই গতিতে সেইদিকে চলতে থাকবে।
2) যদি কোনো বস্তুর ওপর বাহ্যিক বল (external force) F প্রয়োগ করা হয় তাহলে সেই বল (force)-এর দিকে তার ত্বরণ (accelaration) হবে ‘a ’। এই ত্বরণের মাপ পাওয়া যাবে F = ma সম্পর্কটি থেকে। এখানে ‘m’ হলো বস্তুর ভর (mass)। [এই ভরকে সাধারণত inertial mass বলে – inertia (জাড্য) হচ্ছে কোনো পরিবর্তনের বিরোধিতা করা। বাইরে থেকে প্রযুক্ত বলকে একটি বস্তু কতটা উপেক্ষা করতে পারবে, এই inertial mass তারই মাপকাঠি।] যখন F = ma লেখা হলো, তখন ধরে নেওয়া হলো F-এর প্রয়োগকালে বস্তুর ভরের পরিবর্তন হচ্ছে না। যদি হয় তাহলে নিউটনের সূত্র বলে: বল (force) হচ্ছে বস্তুটির ভরবেগ (momentum)-এর পরিবর্তনের হার।
3) দুটি বস্তু যদি একে অপরের উপর বল প্রয়োগ করে, তাহলে বল দুটির মান সমান এবং তাদের দিকগুলি বিপরীত (equal and opposite)।
এইবার শুরু হলো গন্ডগোল। ভর অপরিবর্তিত ধরে নিয়ে নিউটনের দ্বিতীয় সূত্র লেখা হলো:
ত্বরণ (acceleration) ‘a ’ হচ্ছে বেগের পরিবর্তনের হার । [উল্লেখযোগ্য যে F, a সব-ই ভেক্টর, এদের মান (magnitude) এবং দিক (direction) দুই আছে কিন্তু আমরা নেহাত প্রয়োজন না হলে ভেক্টর ব্যবহার করব না – ধরে নেওয়া হবে ‘F’ যেদিকে, ‘a’-ও সেইদিকে।] Eq. (1)-এ F=0 মানে
, অতএব
অপরিবর্তিত – তাহলে আমরা নিউটনের প্রথম সূত্রতে পৌঁছে গেলাম। নিউটন জোর করে অথবা ভুল করে তাঁর প্রথম সূত্র লিখেছিলেন – এটি পদার্থবিদ্যা শেখানোতে ভারতীয় শিক্ষক সমাজের অধিকাংশের চরম লজ্জাজনক অবদান।
কেন এই ভুল হলো? এইবার সেটা বোঝার জন্য প্রথমেই দরকার রেফারেন্স ফ্রেম (reference frame) – আমি যদি কোনো বস্তুর অবস্থান বা গতি বা ত্বরণ মাপতে চাই, তাহলে প্রথমেই প্রয়োজন একটি coordinate system-এর এবং একটি ঘড়ির (ধরে নেওয়া হবে ঘড়িটা সকলের সমান)। কিন্তু প্রত্যেকের coordinate system তার নিজস্ব। আমি যদি মাটিতে দাঁড়িয়ে থাকি, তাহলে একটি চলমান বাসের গতি মাপতে পারি ঘন্টায় কুড়ি কিলোমিটার। কিন্তু আমি যদি ঐ একই বেগে চলা একটি গাড়ি থেকে দেখি, তাহলে দেখব বাসের গতি শূন্য। যে একটি বস্তুর গতি দেখছে তাকে আমরা বলব observer (দর্শক, পরীক্ষক এই ক্ষেত্রে) এবং যে coordinate system ও ঘড়ি সে ব্যবহার করছে, সেটা হবে তার reference frame। Observer এবং frame, এই দুটো শব্দের যে কোনো একটি ব্যবহার করা হবে – এই লেখার জন্য তাদের মানে এক। এইবার second law এর জন্য একটি সতর্কবাণী বলা যাক –
নিউটনের দ্বিতীয় সূত্র, external force F = ma কেবলমাত্র সেই observer (অথবা সেই frame)-এর জন্য সত্যি যার জন্য প্রথম সূত্রটা সত্যি।
যে observer (বা frame) এর জন্য বাহ্যিক বল F = ma সেই observer (বা frame)-কে বলা যাক inertial observer (বা inertial frame of reference)। নিউটনের প্রথম সূত্র অনুযায়ী inertial frame এর সংজ্ঞা হলো এই: Inertial frame হল এমন একটা frame যেখানে বাহ্যিক বল না থাকলে গতির কোনো পরিবর্তন হয় না।
এবার একটা উদাহরণের সাহায্যে এই তথ্যগুলি বোঝা যাক। মাটির উপর রাখা আছে একটা M ভরের টেবিল। তার উপরটা অত্যন্ত মসৃণ (smooth)। টেবিলের উপর রাখা আছে একটা m ভরের বাক্স। বাক্সের তলাটিও মসৃণ। তাই টেবিলের সাথে তার কোনো ঘর্ষণ বল নেই। সব কিছু স্থির।
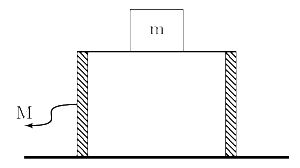
এবার টেবিলের উপর ডানদিকে একটা ধ্রুবক বাহ্যিক বল (constant external force) F প্রয়োগ করা হলো। আমরা দুজন observer (পর্যবেক্ষক) এর দৃষ্টিভঙ্গি থেকে পরবর্তী ঘটনাগুলি দেখব। Observer A দাঁড়িয়ে আছে মাটিতে – টেবিল থেকে একটু দূরে। বাক্স যদি থাকে টেবিলের মাঝ বরাবর তাহলে A-র অবস্থান-ও তাই। Observer B বসে আছে টেবিলের উপর – টেবিলের এই জায়গাটি থেকে নড়ার উপায় নেই তার।
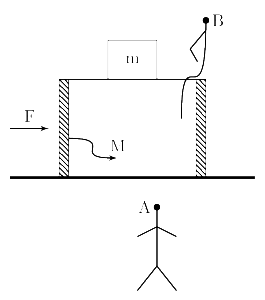
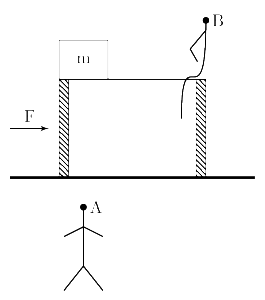
Figure 2-এ এই ব্যাপারটা আমরা দেখছি যে মুহূর্তে বল প্রয়োগ করা হলো সেই মুহূর্তে। একটু পরে কি ঘটবে সেটা figure 3-এ রয়েছে। এবার আমরা A এবং B- এর দৃষ্টিভঙ্গি আলাদা করে বিশ্লেষণ করব।
Observer A : A-এর মতে টেবিলের উপর পড়ছে বাহ্যিক বল F। তাই টেবিলের ত্বরণ a = F/M ডানদিকে। Figure 3-তে দেখো, টেবিল ডানদিকে সরেছে। কিন্তু বাক্স আর টেবিলের মধ্যে কোনো ঘর্ষণ বল নেই। তাই বাক্সটির উপর বাহ্যিক বল F-এর কোনো প্রভাব পড়বে না। বাক্সটি যেখানে ছিল সেখানেই থাকবে। তার কোনো স্থান পরিবর্তন হবে না। Figure 3-এর পরের মুহুর্তে বাক্সটি টেবিল থেকে পরে যাবে। নিউটন-এর দ্বিতীয় সূত্রটি observer A হুবুহু মেনে চললো – তাই observer A হচ্ছে inertial observer।
Observer B : B চলেছে টেবিলের সঙ্গে – সে কিন্তু নিজের গতিরেখা সম্বন্ধে কিছু জানে না। শুধু দেখবে বাইরেটা ক্রমশ বাঁদিকে সরে যাচ্ছে! আর বাক্সটা ? তার উপর তো কোনো বাহ্যিক বল নেই। অথচ তার ত্বরণ মাপলে B দেখবে বাক্সের ত্বরণ বাঁদিকে a = F/M! কেন ? নিউটন-এর দ্বিতীয় সুত্র B-এর জন্য কেন প্রযোজ্য হলো না A-এর মত ?
এই অমিলের সমাধান: B-কে inertial observer বলব না আমরা। কাকে inertial observer বলা যাবে আর কাকে যাবে না, এটা বুঝতে গেলে B-এর উপর মনোনিবেশ করা যাক। লক্ষণীয়, একজন inertial observer (A)-এর কাছে B-এর ত্বরণ আছে। অতএব ধরে নেওয়া যাক, একটা inertial frame-এর দৃষ্টিতে একটা observer (বা frame)-এর যদি ত্বরণ থাকে, তাহলে সেই observer-কে non-inertial বলা হবে। F = ma, এই মর্মে নিউটন-এর দ্বিতীয় সুত্র তার জন্য প্রযোজ্য হবে না। এবার প্রশ্ন একটি : একজন non-inertial observer, যে a ত্বরণে চলেছে, নিউটনের দ্বিতীয় সুত্র কিভাবে লিখবে ? (এখানে a কে স্থূল হরফে লেখা হলো, কারণ ত্বরণের মান ও দিক দুটোই আছে-এটি একটি ভেক্টর।)
এই প্রশ্নটির উত্তরে non-inertial observer বলবে, তার নিজের ত্বরণের জন্য প্রত্যেকটি বস্তুর উপর একটি বল কাজ করছে, যাকে সে লিখবে
হিসাবে, যদি বস্তুটির ভর হয় m। এই subscript p টা আমাদের মনে করিয়ে দিচ্ছে যে সত্যিকারের বল নয়। তবে এই বলটিকে non-inertial observer-কে ধরতে হবে যদি তাকে নিউটন-এর দ্বিতীয় সূত্র লিখতে হয়। এই বলকে তাই আমরা বলব ছদ্মবল বা Pseudo force। তাই একজন Non-inertial observer নিউটন-এর দ্বিতীয় গতিসূত্র লিখবে এইরকম:
আবার Fig. (2) এবং Fig. (3) observer B-এর দৃষ্টিভঙ্গি থেকে দেখা যাক। B দেখবে m এর উপর কোনো external force নেই। কিন্তু তার নিজের ত্বরণের জন্য সে বাক্সটির জন্য নিউটনের দ্বিতীয় সূত্র লিখবে
অর্থাৎ, বাক্সটির ত্বরণ সে দেখবে বাঁদিকে । এই dynamics-টাই Fig (2) এবং Fig (3)-এ B-এর চোখে ধরা পড়ছে।
এইবার ধরা যাক টেবিল ও বাক্সের মধ্যে friction (ঘর্ষণবল) রয়েছে। টেবিলটিকে ঠেললে টেবিল বাক্সের তলা দিযে চলে যাওয়ার চেষ্টা করবে, কিন্তু friction থাকায় এই প্রচেষ্টায় বাধা আসবে। তাই বাক্স টেবিলের ওপর friction force ( ) প্রয়োগ করবে বাঁদিকে – যেদিকে টেবিল যেতে চায়, তার উলটো দিকে। এবার যদি টেবিলের উপরে external force-গুলি (ডাইনে ও বাঁয়ে) আঁকা যায় তাহলে ছবিটি হবে এইরকম:
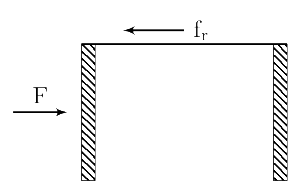
এবং যদি টেবিলটি ডান দিকে চলতে পারে, তাহলে
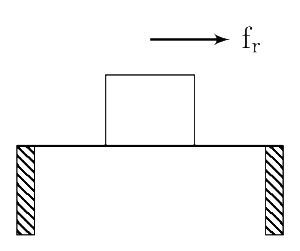
যেখানে ‘a’ হচ্ছে টেবিল এর ত্বরণের মান।
বাক্সটির কি হবে? তার ওপর নিউটনের তৃতীয় সুত্র অনুযায়ী force কাজ করবে ডাইনে (equal and opposite)। যদি একই সঙ্গে টেবিল ও বাক্স চলে, তাহলে টেবিল ও বাক্সের ত্বরণ সমান। অর্থাৎ,
Eqs. (5) এবং (6) যোগ করলে,
অর্থাৎ, system-টা একটিই বস্তুর মত ব্যবহার করছে যার ভর ।
কিন্তু বাক্স ও টেবিলের মধ্যে friction-এর একটি সর্বোচ্চ মান আছে। সেই মানটি হচ্ছে যেখানে N হচ্ছে বস্তুটির উপর normal reaction। যেহেতু উপরের দিকে বাক্সটির কোনো গতি নেই,
এবং
Eqs. (6) এবং (7) ব্যবহার করলে
অথবা,
এর মানে কি? ধরা যাক
force-টি
এর চেয়ে বড়,
। তাহলে Eq. (5) এর চেহারা হবে,
Eqs.(8) এবং (9) এর সাহায্যে,
অথবা,
বাক্সের ত্বরণ কত? তার উপর friction force সর্বোচ্চ হওয়ার পর আর বাড়তে পারবে না, তাই (Eqs.(6) এবং (8) দেখ)। এবার
হলে,
, এবং বাক্সটি পিছিয়ে পড়বে টেবিলের অনুপাতে। তাই friction-এর বলে প্রথমে (
) বাক্সটি টেবিলের সঙ্গে এগোবে এবং তারপর (আপাতদৃষ্টিতে) বাঁদিকে চলতে থাকবে এবং অবশেষে পড়ে যাবে।
এবার observer B কি দেখবে? যতখন , B দেখবে বাক্সটি ঠিক যেখানে ছিল সেখনেই রয়েছে। যখন
, তখন সে দেখবে বাক্সের উপর দুটি বল,
একটি বাঁদিকে এবং অন্যটি
ডান দিকে। Eq.(11) অনুযায়ী ‘a’ ধরা হলে, B পাবে
অথবা,
বাক্সটি ত্বরণ (acceleration) নিয়ে বাঁদিকে গিয়ে টেবিল থেকে পড়ে যাবে।
Cover photo (Alexander Borek, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons)। ফোর্স ডায়াগ্রাম: শুভায়ু আলি

